超详细的对比学习综述

每天给你送来NLP技术干货！

---

本文转载自 | 知乎

作者 | 光某人

地址 | https://zhuanlan.zhihu.com/p/346686467

A

『引入』

深度学习的成功往往依赖于海量数据的支持，其中对于数据的标记与否，可以分为监督学习和无监督学习。

1. 监督学习：技术相对成熟，但是对海量的数据进行标记需要花费大量的时间和资源。

2. 无监督学习：自主发现数据中潜在的结构，节省时间以及硬件资源。

2.1 主要思路：自主地从大量数据中学习同类数据的相同特性，并将其编码为高级表征，再根据不同任务进行微调即可。

2.2 分类：

2.2.1生成式学习

生成式学习以自编码器(例如GAN，VAE等等)这类方法为代表，由数据生成数据，使之在整体或者高级语义上与训练数据相近。

2.2.2对比式学习

对比式学习着重于学习同类实例之间的共同特征，区分非同类实例之间的不同之处。

与生成式学习比较，对比式学习不需要关注实例上繁琐的细节，只需要在抽象语义级别的特征空间上学会对数据的区分即可，因此模型以及其优化变得更加简单，且泛化能力更强。

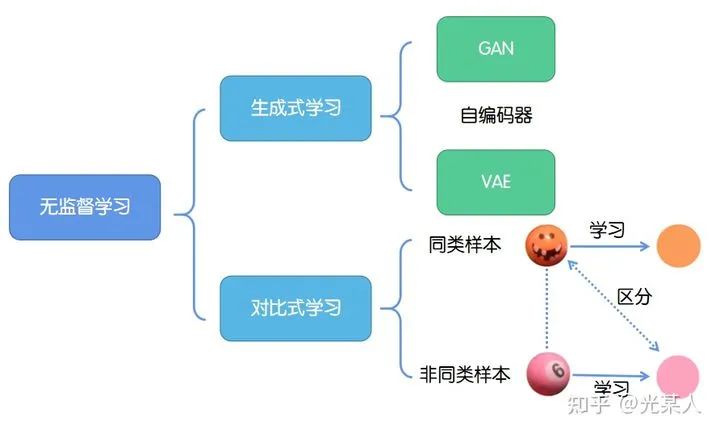
对比学习的目标是学习一个编码器，此编码器对同类数据进行相似的编码，并使不同类的数据的编码结果尽可能的不同。

3. 近况

最近深度学习两巨头 Bengio 和 LeCun 在 ICLR 2020 上点名 Self-Supervised Learning（SSL，自监督学习） 是 AI 的未来，另外，Hinton 和 Kaiming 两位神仙也在这问题上隔空过招，MoCo、SimCLR、MoCo V2 打得火热，这和 BERT 之后，各大公司出 XL-Net、RoBerta 刷榜的场景何其相似。

4.感谢

写这篇综述，花了大概一个多月时间整理【刚大二，有篇复旦的论文确实看不懂，这里就没写】，感谢各位大佬的博客，给了我莫大的帮助，还有学长 @忆臻 和同学 @认真玩家 的鼓励，才让我有信心肝完这篇国内资料不那么完善的综述。

本文对目前的对比学习相关，尤其是NLP方面的工作进行较为全面的介绍，希望能够为感兴趣的同学提供一些帮助。

B

『对比引入』

【拿我的画举个例子】我们可以看到下面两张图的马头和精细程度都是不同的，但是我们显然能判断这两张是类似的图，这是为什么呢

对于某个固定锚点x来说，其位置是由与其他点相对位置决定的，而不是画布的绝对位置。

A中与 x 邻近的点在B图中相应点距 x' 距离小，A中与 x 相距较远的点在B图中相应点距 x' 距离大。

在一定误差范围内，二者近似相等。

可以这么认为，通过对比学习，忽略了细节，找到并确定所以关键点相对位置。

C

『聚类思想』

在这里，我们将之前的想法进行抽象，用空间考虑对比学习。

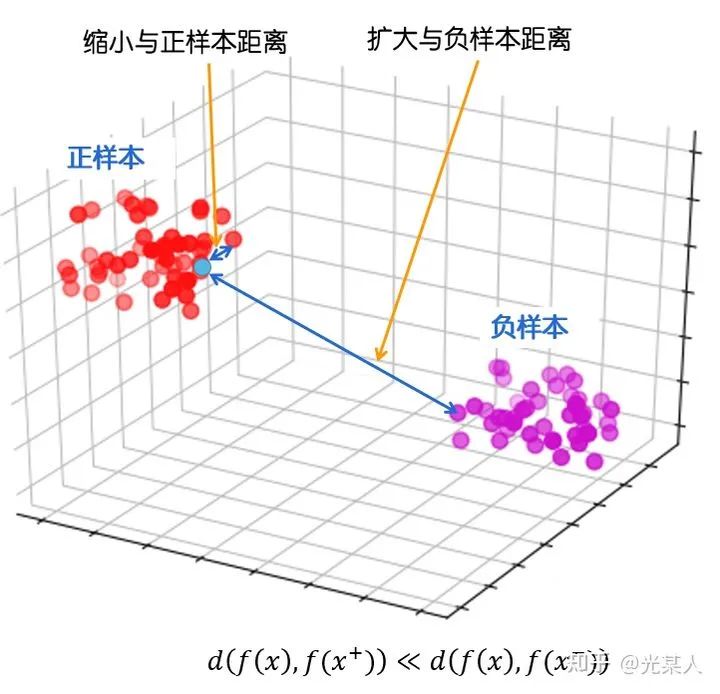
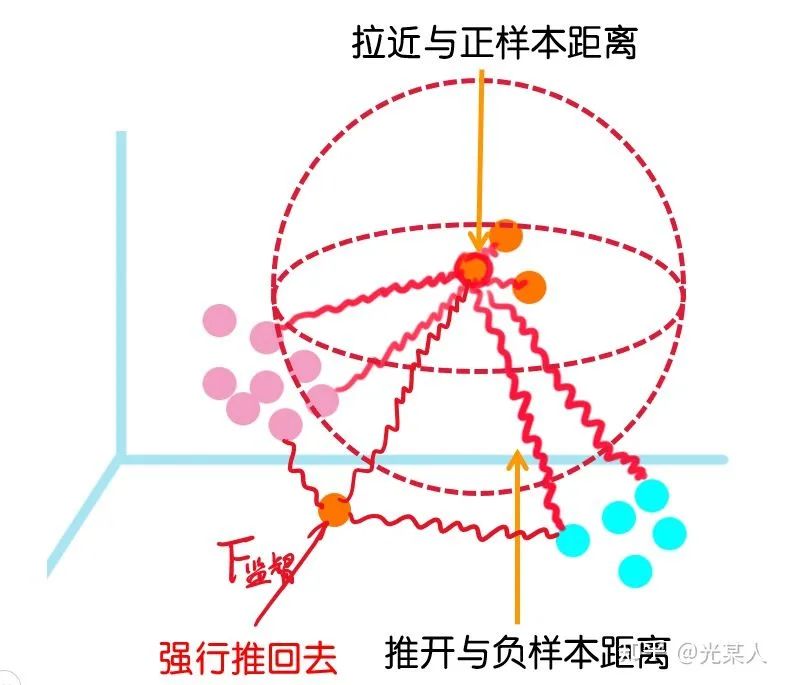
最终目标:

缩小与正样本间的距离，扩大与负样本间的距离，使正样本与锚点的距离远远小于负样本与锚点的距离，（或使正样本与锚点的相似度远远大于负样本与锚点的相似度），从而达到他们间原有空间分布的真实距离。

• 丈量二者距离：欧几里得距离，余弦相似度，马氏距离（没人试过，但原理是一样的）

• 目标：给定锚点，通过空间变换，使得锚点与正样本间距离尽可能小，与负样本距离尽可能大

D

『对比思想』

动机：人类不仅能从积极的信号中学习，还能从纠正不良行为中获益。

对比学习其实是无监督学习的一种范式。根据经典的SIMCLR，我在这里就直接提供了对比学习中模型的常见形式。

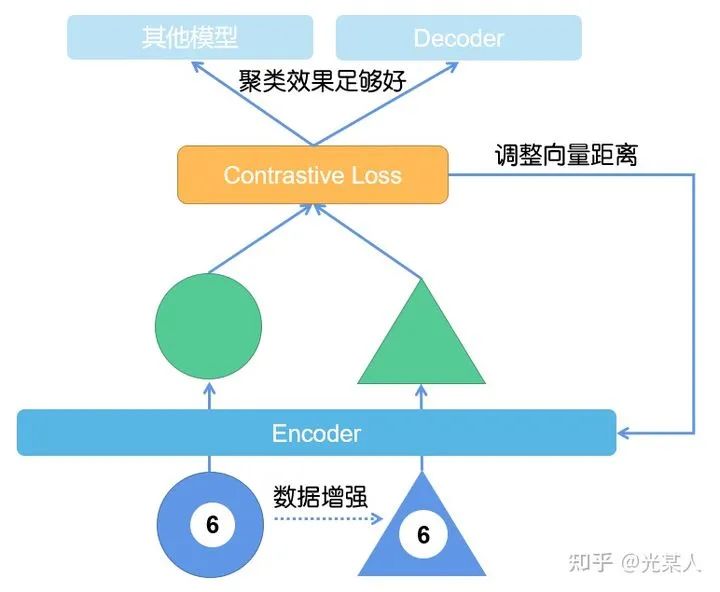
E

『对比损失』

本章的数学公式可以只看结论（NCE可以不看），如果想了解细节请仔细阅读【附录】，如果不懂可以评论私信，或者移步参考博客学习。

1. 欧几里得距离

在线性空间中，上述相似度就可以表示为二者向量间的欧几里得距离：

2. 对比损失定义

由Hadsell, R. , Chopra, S. , & Lecun, Y. . (2006)提出[1] ,原文只是作为一种降维方法：只需要训练样本空间的相对关系（对比平衡关系）即可在空间内表示向量。

损失定义如下：

为了下文方便解释，这里的参数详细解释如下：

 ：网络权重；

 ：标志符，

 ：是  与  在潜变量空间的欧几里德距离。

 ：表示第i组向量对。

 ：研究中常常在这里做文章，定义合理的能够完成最终目标的损失函数往往就成功了大半。

2.1 细节定义

  只需满足红色虚线趋势。

 只需满足蓝线趋势【都有趋于0的区域】。

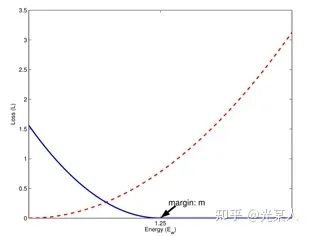
2.2 过程/主流程

原文类比弹性势能，将正负样本分类讨论。

正样本：

当与锚点是正样本时，由于对比思想，二者之间会逐渐靠近。原文将它假设成一个原长  的弹簧，那么就会将正样本无限的拉近，从而完成聚类。

将锚点设为势能零点：

那么 E 即可作为 ，且满足定义要求：

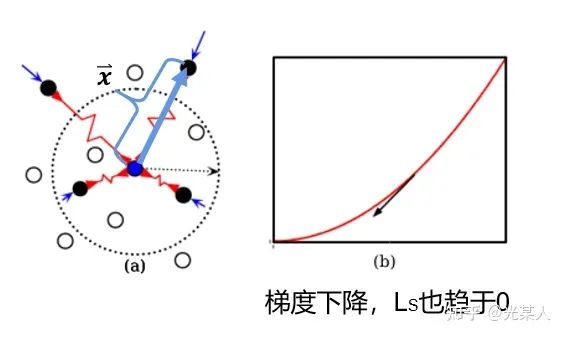
负样本

当与锚点是负样本时，由于对比思想，二者之间会逐渐原理。原文将它假设成一个原长  的弹簧，那么就会将负样本至少拉至m，从而完成划分。

将锚点设为势能零点：

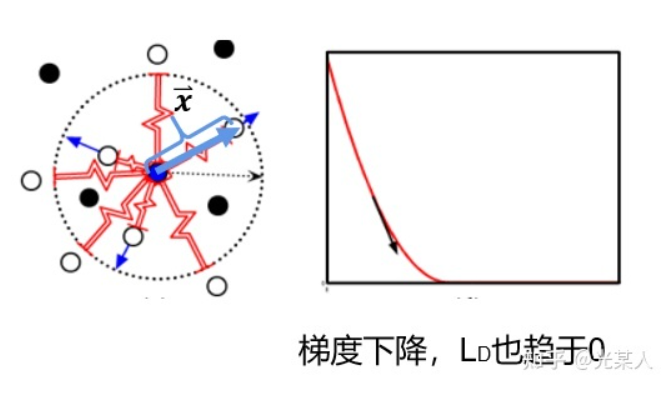
L原定义:

这样我们就获得了Loss函数最基本的定义：

当Y=0，调整参数最小化  。

当Y=1，设二者向量最大距离为m，

如果  , 则增大两者距离到m；

如果  ，则不做优化。

空间角度：

空间内点间相互作用力动态平衡。

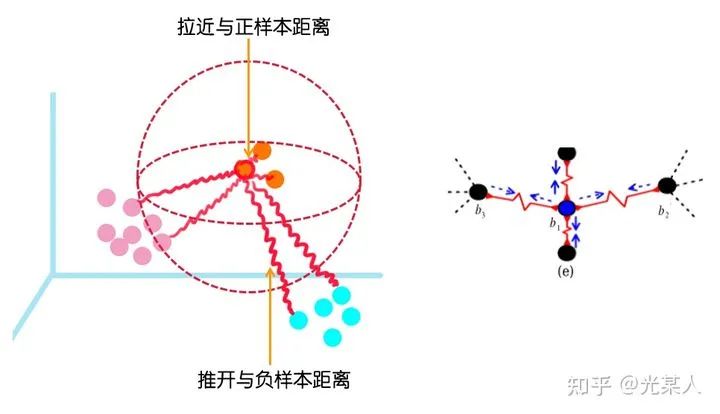
2.3 效果

我们可以看到，和4不那么像的9会被拉远离4，和4相似的9会在交界面上十分接近地分布。这和我们的的对比想法是一致的。

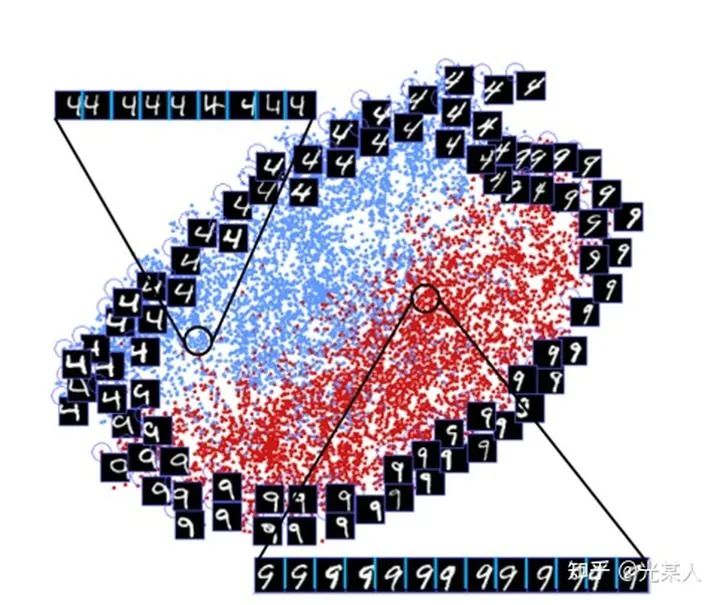
同时，该论文还发现许多对比学习中有趣的现象。

不同光照下，不同角度下，像素间欧氏距离尽管很远，但是能聚集在一个环上。

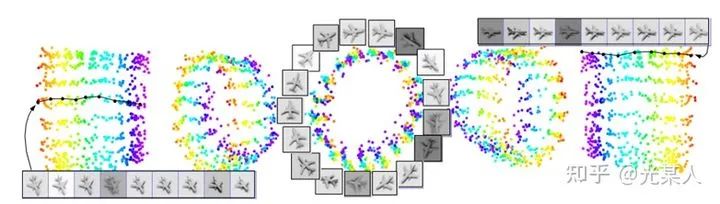
3. Triplet Loss

（简化版原方法）

结论

我们将三元组重新描述为  。

那么三元组的总体距离可以表示为：【近年论文好像也有沿用的，比较经典】

相较定义来说，Triplet Loss认为，假如所有正样本之间无限的拉近，会导致聚类过拟合，所以，就只要求

当然在比例尺上看来，  也会趋于0。

原文将所有三元组的状态分为三类：

• hard triplets
  正样本离锚点的距离比负样本还大

• semi-hard triplets
  正样本离锚点的距离比负样本小，但未满足

• easy triplets
  满足 

前两个状态会通过loss逐渐变成第三个状态。

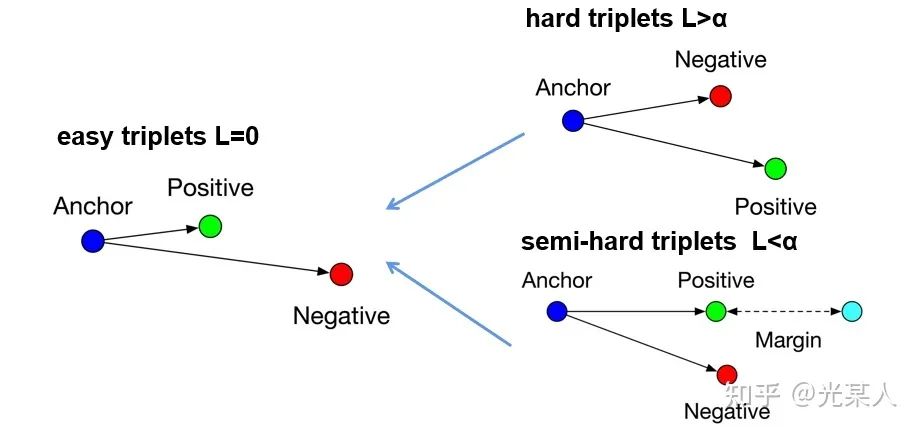
4. NCE Loss

【注：后续研究并没有怎么使用原始的NCELoss，而是只使用这里的结论，这里引入是为了说明应该多采用负样本。】

之前从向量空间考虑，NCE从概率角度考虑【原证明为贝叶斯派的证法】，NCE是对于得分函数的估计，那也就是说，是对于你空间距离分配的合理性进行估计。

总之NCE通过对比噪声样本与含噪样本，从而推断真实分布。

【与对比学习思想一致，可以当做是另一角度】

结论

 越大，约接近NCE 对于噪声分布的依赖程度也就越小，越接近真实期望。 

5. 互信息

在预测未来信息时，我们将目标x（预测）和上下文c（已知）编码成一个紧凑的分布式向量表示(通过非线性学习映射），其方式最大限度地保留了定义为的原始信号x和c的互信息

通过最大化编码之间互信息(它以输入信号之间的MI为界)，提取输入中的隐变量。

互信息往往是算不出来的，但是我们这里将他进行估计，通过不同方法进行估计，从而衍生出自监督的两种方式：生成式和对比式【详见A 2.2.2】

互信息上界估计：减少互信息，即VAE的目标。

互信息下界估计：增加互信息，即对比学习（CL）的目标。【后来也有CLUB上界估计和下界估计一起使用的对比学习。】

6. InfoNCE Loss

具体详见CPC论文1.3节。

通过二者互信息【详见附录】来衡量二者距离/相似度，可逼近其下界。

结论

后续研究

后续研究的核心往往就聚焦于的两个方面：

• 如何定义目标函数？【详见附录】
  

• 简单内积函数
  

• InfoNCE【近年火热】
  

• triplet 【近年火热】 【知乎的问题，后边的s函数的负号上标可能消失】

• 如何构建正实例对和负实例对？

这个问题是目前很多 paper 关注的一个方向，设计出合理的正实例与负实例对，并且尽可能提升实例对，才能表现的更好。

F

『基础论文』

1. CPC

论文标题：Representation Learning with Contrastive Predictive Coding

论文链接：arxiv.org/abs/1807.0374

代码链接：github.com/davidtellez/

很多时候，很多数据维度高、label相对少，我们并不希望浪费掉没有label的那部分data。所以在label少的时候，可以利用无监督学习帮助我们学到数据本身的高级信息，从而对下游任务有很大的帮助。

Contrastive Predictive Coding（CPC） 这篇文章就提出以下方法：

• 将高维数据压缩到更紧凑的隐空间中，在其中条件预测更容易建模。

• 用自回归模型在隐空间中预测未来步骤。

• 依靠NCE来计算损失函数（和学习词嵌入方式类似），从而可以对整个模型进行端到端的训练。

• 对于多模态的数据有可以学到高级信息。

可以利用一定窗口内的  和  作为正实例对，并从输入序列之中随机采样一个输入作为  负实例。

1.1 问题描述

给定声音序列上下文  ，由此我们推断预测  位置上的声音信号。题目假设，声音序列全程伴随有噪音。为了将噪音序列与声音序列尽可能的分离编码，这里就随机采样获得  代替  位置信号，作为负样本进行对比学习。

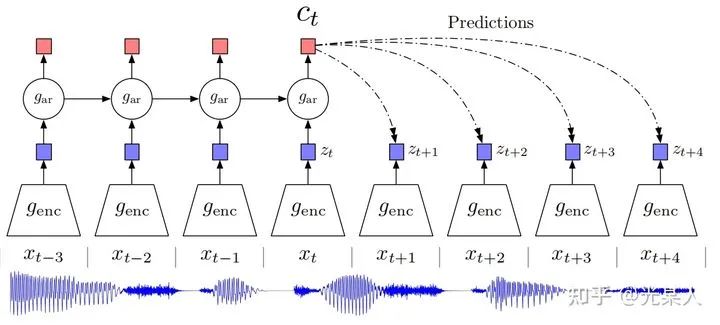
1.2 CPC

下图说明了 CPC 的工作过程：

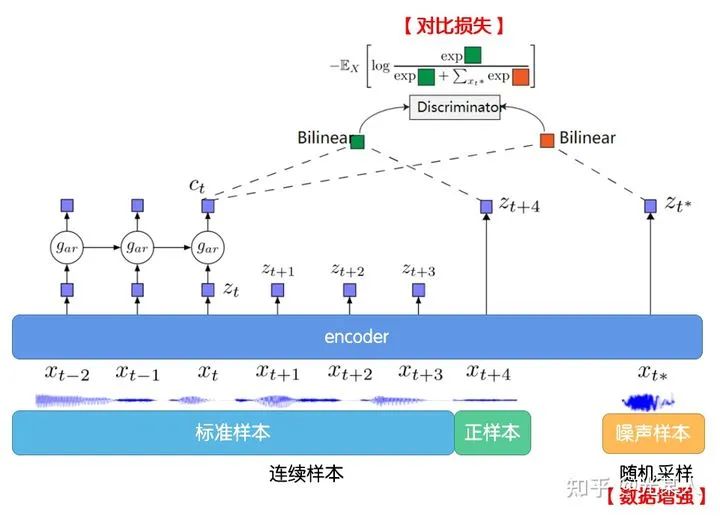
首先我们在原信号上选取一些时间窗口，对每一个窗口，通过encoder  ，得到表示向量  。

 通过自回归模型：  ，从而生成上下文隐变量  。

然后通过Bi-linear：【采用  和  从而能够压缩高维数据，并且计算  和  的未来值是否符合】

1.3 InfoNCE Loss

CPC用到了NCE Loss, 并推广为InfoNCE:（证明见【附录】）

选取  ，这里面只有一个正样本对  来自于  ，即声音原本的信号，其他N-1个均是负样本（噪声样本）来自于 ，即随机选取的信号片段。

损失函数定义如下：【 f 可自由定义，甚至为MLP】

我们用softmax的思路来理解这个损失函数，  越大，应该越接近于0（越接近最大值），而损失就越小。

回到对比学习的思想，W将做c到z的映射，  均经过归一化，那么，二者余弦相似度为  ，这样  ，即可看做softmax，将  正样本的值加大，负样本值缩小。

2. MoCo

论文标题：Momentum Contrast for Unsupervised Visual Representation Learning

论文来源：CVPR 2020

论文链接：arxiv.org/abs/1911.0572

代码链接：github.com/facebookrese

本文提出了高效的对比学习的结构。使用基于 MoCo 的无监督学习结构学习到的特征用于 ImageNet 分类可以超过监督学习的性能。证明了无监督学习拥有巨大的潜力。

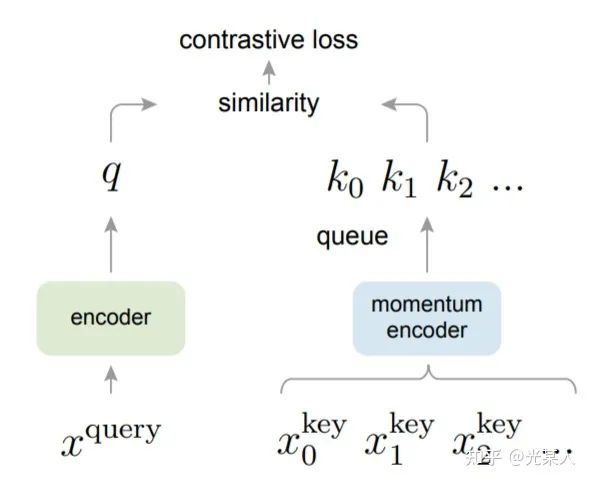
受NLP任务的启发，MOCO将图片数据分别编码成查询向量和键向量，即，查询 q 与键队列 k ，队列包含单个正样本和多个负样本。通过 对比损失来学习特征表示。

主线依旧是不变的：在训练过程中尽量提高每个查询向量与自己相对应的键向量的相似度，同时降低与其他图片的键向量的相似度。

MOCO使用两个神经网络对数据进行编码：encoder和momentum encoder。

encoder负责编码当前实例的抽象表示。

momentum encoder负责编码多个实例(包括当前实例)的抽象表示。

对于当前实例，最大化其encoder与momentum encoder中自身的编码结果，同时最小化与momentum encoder中其他实例的编码结果。

2.1 InfoNCE Loss

这个Loss只能更新q向量的encoder。如果同时更新q和k没有意义。

交叉熵损失：

交叉熵损失(Cross-entropy Loss) 是分类问题中默认使用的损失函数：

分类模型中，最后一层一般是linear layer+softmax。所以如果将之前的特征视为, linear layer的权重视为，则有：

每个权重矩阵  事实上代表了每一类样本其特征值的模板（根据向量乘法我们知道越相似的两个向量其内积越大）。

实际上，现有的分类问题是通过一系列深度网络提取特征，然后依据大量的样本学习到一个有关每一类样本特征的模板。在测试的阶段则将这个学到的特征模板去做比对。

非参数样本分类：

所谓非参数样本分类，则是将每个计算出的样本特征作为模板，即看做是计算所得的样本特征模板。

对比损失：

我们最终的目标还是不变的：

这里与CPC类似地，我们使用cosine距离，假设已经归一化特征值，则优化上式实际上等同于最大化下式中的softmax概率，

假设其中有一个正样本  其余均是负样本，则根据 InfoNCE Loss表示为：

其中  和  可以有多种构造方式，比如对图像进行裁剪变色等随机变化。

但是呢，实现上来说，将  看做一体为  ，那么  ，即为交叉熵损失。

2.2 Memory Bank

由于对比学习的特性，参与对比学习损失的实例数往往越多越好，但Memory Bank中存储的都是 encoder 编码的特征，容量很大，导致采样的特征具有不一致性（是由不同的encoder产生的）。

所以，对所有参与过momentum encoder的实例建立动态字典(dynamic dictionary)作为Memory Bank，在之后训练过程中每一个batch会淘汰掉字典中最早被编码的数据。

2.3 Momentum 更新

在参数更新阶段，MOCO只会对encoder中的参数进行更新。

由于Memory Bank，导致引入大量实例的同时，会使反向传播十分困难，而momentum encoder参数更新就依赖于Momentum 更新法，使momentum encoder的参数逐步向encoder参数逼近：

其中  ，  指encoder部分的参数。

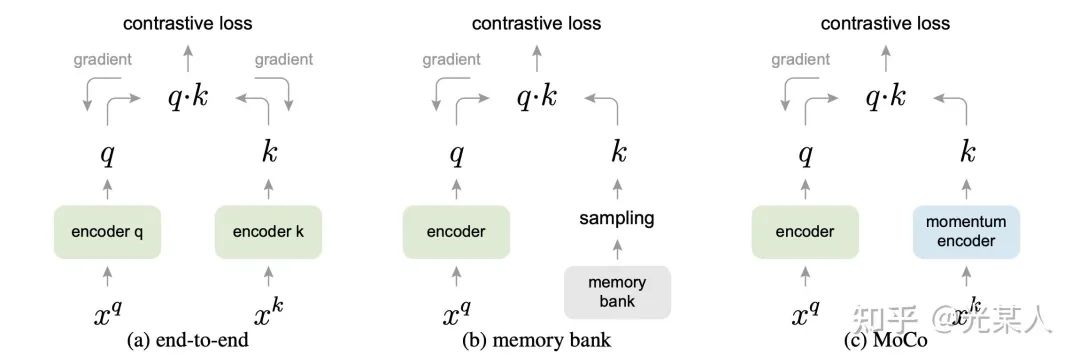
下图形式化的表示了三种结构，end-to-end，memory-bank和MoCo的区别。MoCo的特点是：

（1）用于负采样的队列是动态的

（2）用于负样本特征提取的编码器与用于query提取的编码器不一致，是一种Momentum更新的关系。

（3）与Memory Bank类似，NCE Loss只影响 Query ，不更新key。

2.4 代码流程

3. SimCLR

论文标题：A Simple Framework for Contrastive Learning of Visual Representations

论文链接：arxiv.org/abs/2002.0570

代码链接：github.com/google-resea

https://vdn1.vzuu.com/SD/0f5cab40-75af-11eb-ab9c-3e1a43f1851b.mp4?disable_local_cache=1&auth_key=1619885825-0-0-4551405ef8b2d654e21c537843374ab5&f=mp4&bu=pico&expiration=1619885825&v=hw

3.1 做法：

simCLR背后的想法非常简单：

视觉表征对于同一目标不同视角的输入都应具有不变性。

simCLR对输入的图片进行数据增强，以此来模拟图片不同视角下的输入。之后采用对比损失最大化相同目标在不同数据增强下的相似度，并最小化同类目标之间的相似度。

用下面这张图来说明：

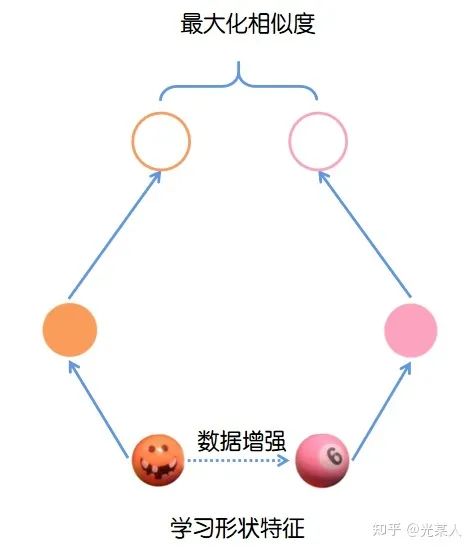
simCLR的架构由两个相同的网络模块组成。对于每一个输入网络的minibatch:

1. 对mini batch中每张输入的图片进行两次随机数据增强(随机剪裁、滤镜、颜色过滤、灰度化等)来得到图片两种不同的视角;
   

2. 将得到的两个表征送入两个卷积编码器(如resnet)获得抽象表示，之后对这些表示形式应用非线性变换进行投影得到投影表示;
   

3. 使用余弦相似度来度量投影的相似度。
   

simCLR使用了多组对比，直接加强了效果【可以看成完全图，将相邻点拉近，不相似的点拉开】：

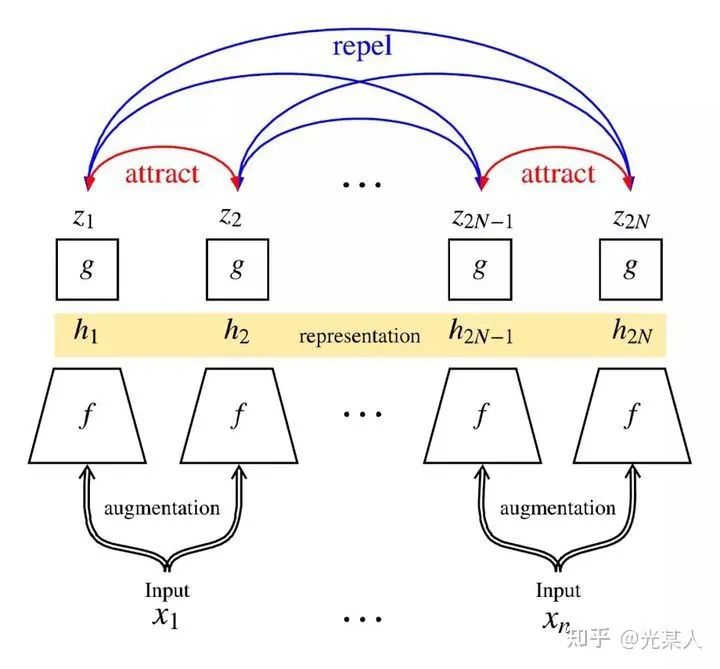
由此可以得到优化目标：对于minibatch中同一图片，最大化其两个数据增强投影的相似度，并最小化不同图片之间的投影相似度。

3.2 思想

以我的角度看，SimCLR的思想是值得借鉴的：

表示学习中，表示向量如果在空间内相对确定，那么在绝对空间中是较为准确的。

我们可以认为，是向量空间中的其他点决定了锚点的正确位置。做个比喻，你在学术界的人际关系，和同行评价决定了你所处的学术地位。【尽管这些是由你的科研工作决定的，但也是相对真实的反映了你的地位】。

但是，如果参考点过少，位置的确定则过于片面。所以，SimCLR的batch-size也达到了8192，用了128块TPU，又是算力党的一大胜利。

3.3 代码

4. 神仙打架

4.1 MoCo-v2

MoCo v2 也是利用了上面SimCLR的第一点和第三点，并在MoCo-v1的基础上，将余弦相似度更换为一层MLP。在 MoCo 基础上得到了进一步的提升，然后作者还也明确的点名了 SimCLR，称不需要使用那么大的 batch size 也能超过它，可能这就是神仙打架吧。

4.2 SimCLR-v2

知识蒸馏

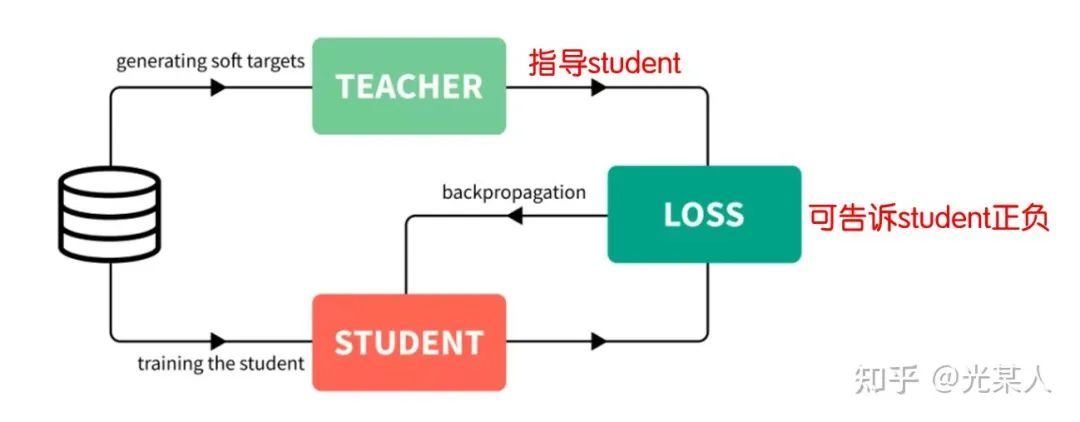
具体结构

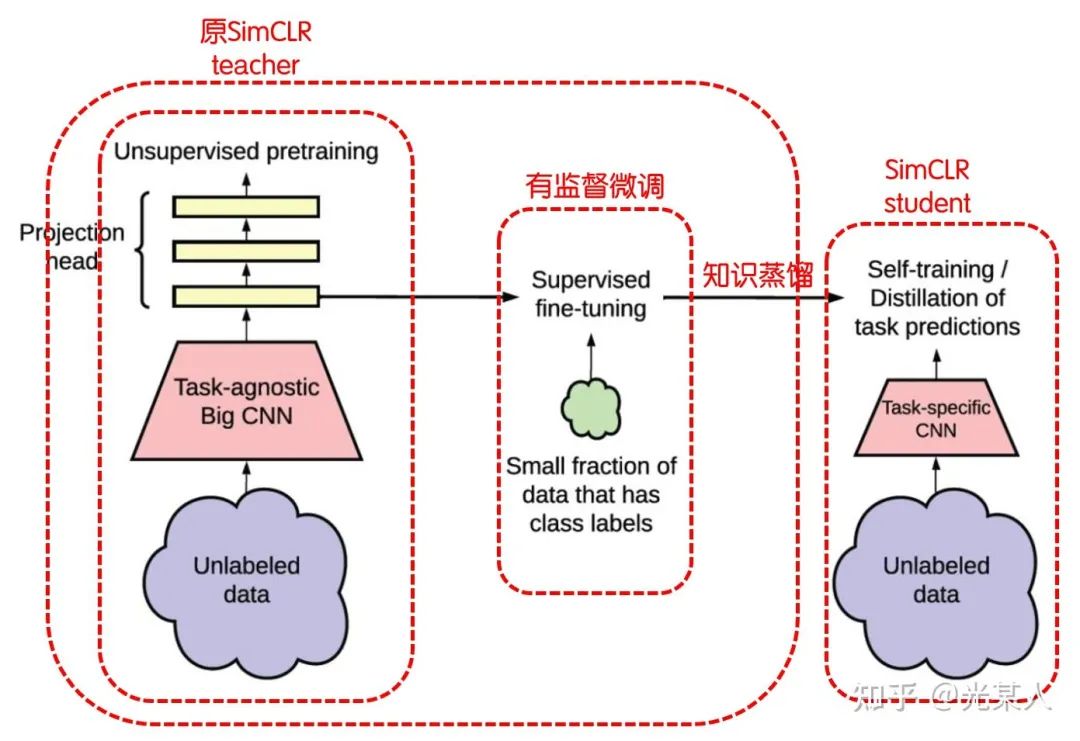
5. 有监督对比学习

论文标题：Supervised Contrastive Learning

论文链接：https://arxiv.org/abs/2002.05709

5.1 动机

之前的论文都是自监督学习，自监督只做自己的变换，可能会过拟合。比如会把另一个品种的够对比到另一个类。

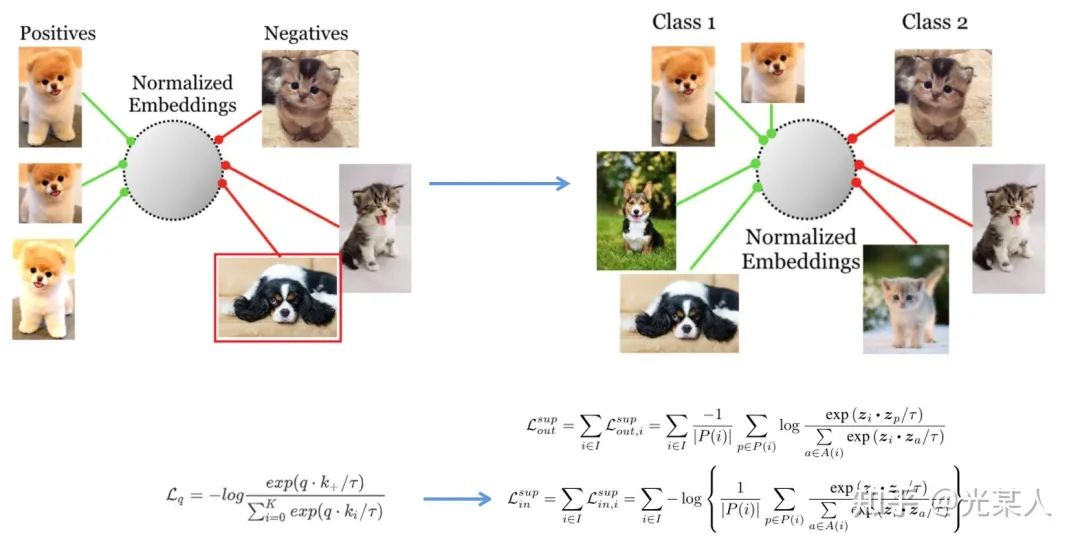
5.2 想法

5.3 证明

该论文还证明了Triplet Loss和InfoNCE Loss近似等价，统一了理论。

如果InfoNCE Loss中k=1，则：

6. 后续研究

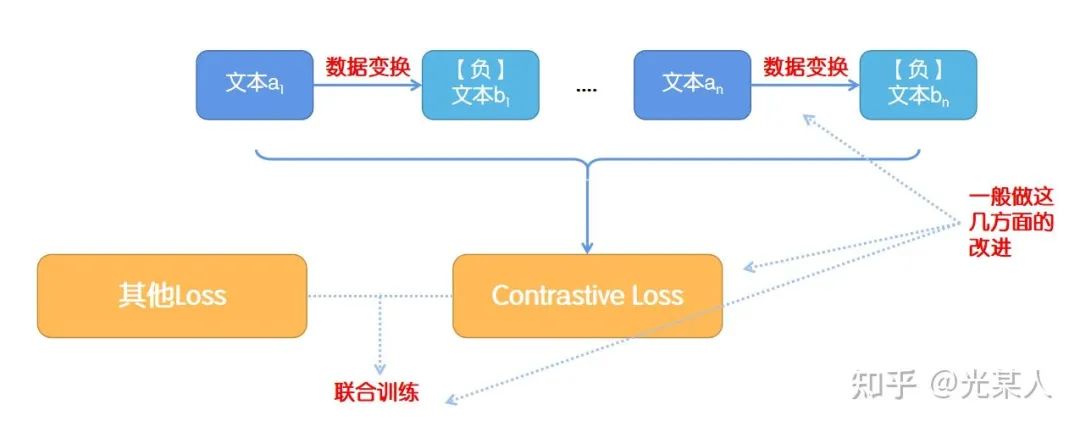
6.1 主线

拉大正负样本的距离

6.2 后续研究核心

1. 如何定义目标函数？【详见附录】

• 简单内积函数

• InfoNCE【近年火热】

• triplet 【近年火热】

2. 如何构建和实现正实例对和负实例对？
这个问题是目前很多 paper 关注的一个方向，设计出合理的正实例与负实例对，并且尽可能提升实例对，才能表现的更好。

3. 联合其他模型作为较为准确的向量空间通过对比学习微调。

6.3 重兴原因

• BERT等预训练模型成效显著 [核心3]

• 数据变换有了一些评估模型作为依据 [核心2]

• 提出了更好的Loss函数 [核心1]

• 其他模型的改进效应 [核心3]

• MoCo解决了对比学习大量负样本带来的更新缓慢的问题 [核心2]

6.4 联合模型思考

由于对比学习是对相对空间中的向量表示，单纯地运算相对关系算力要求很高【SimCLR暴力美学证明可以纯算，但一般做不起】，一般作为其他模型绝对空间相对准确后的对任务的相对微调。

比如说，Bert能使空间词向量绝对空间的位置，相对准确，但是针对某些任务，它的聚类效果不够好，我们使用对比学习调整它们间的相对关系，从而适应我们的任务。

G

『NLP近年论文』

【这里仅做总括，细节会迁到另一篇博客，毕竟太长没人看】

老鸽子终于想起来更新了，论文会慢慢的放出来，如果觉得讲得不好，请大家海涵，可以积极的和我讨论，分析格式我也会根据评论调整的！

https://zhuanlan.zhihu.com/p/363900943

由于NLP一般进行数据增强时，负例构造比较容易，而且NCE Loss也鼓励负例构造。这里就做了一些NLP处理方法的一些统计【至2021.2】。

H

『附录』

头疼的数学都放在这里啦！！

互信息

假设  ，  为X的信息熵，  为条件熵，信息表述如下：

如果X与Y有关联，则Y已知的条件下，X的不确定性会变化。

若设X,Y的联合概率分布为p(x,y)，边缘概率为p(x),p(y)概率分布可以表示为：

互信息与信息熵的关系：

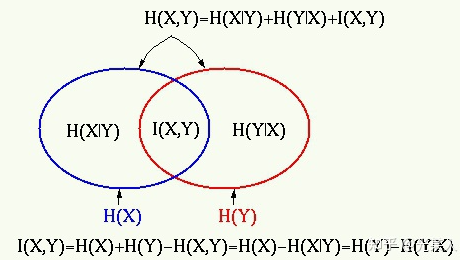
通常我们使用的最大化互信息条件，就是最大化两个随机事件的相关性。

互信息上界

VAE估计

VAE的思想是用  【一般取正态分布】去变分估计  ，为了衡量二者分布的相似程度，这里用KL散度进行比较。【注：KL散度统计意义上永远大于等于0】

即  ，所以

CLUB估计[ICML2020]

由于没有进行先验估计，所以是更加紧的上界。

由于log函数是凹函数，根据 Jensen 不等式：

因此：

对比损失的一些分类

Triplet Loss

结论

我们将三元组重新描述为  。

那么最小化损失就是使  。

那么三元组的总体距离可以表示为：【近年论文好像也有沿用的，比较经典】

原理

Triplet Loss，即三元组损失，是Google在2015年发表的FaceNet论文中提出[2]。

定义：最小化锚点和具有相同身份的正样本之间的距离，最小化锚点和具有不同身份的负样本之间的距离。

主线：使相同标签的特征在空间位置上尽量靠近，同时不同标签的特征在空间位置上尽量远离。

同时为了不让样本的特征聚合到一个非常小的空间中，要求对于同一类的两个正实例和一个负实例，负例应该比正例的距离至少为margin值  。如下图所示：

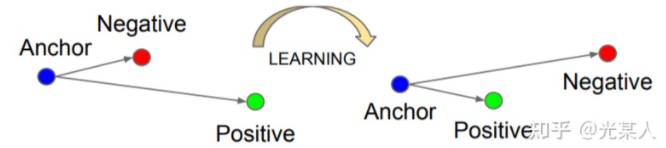
因为我们期望的是下式成立，即：【给不记得欧几里得范数的兄弟补个知识：  】

  为样本容量为N的数据集的各种三元组。

根据上式，Triplet Loss可以写成：

对应的针对三个样本的梯度计算公式为： 

这样我们可以看到这些个三元组的关系是联系紧密，又对称的。

NCE Loss

【这部分证明参考[b]博客，这位大佬写的非常详细，这里做了一些简化方便讲解。】

结论

推导【觉得复杂可以跳过】

NCE，也就是 Noise Contrastive Estimate（噪声对比估计）[3]中提出，不过是连续的概率密度函数。由[4]提出了其离散分布时的表现形式，将 NCE 应用到 NLP 领域。

对于n-grams语言模型（n元语法），设单词序列为  ，  为上下文  ，满足：

设 

那么上式的最大似然函数为

那么最关键的F该怎么求呢？

设  为量化 w与c 匹配性的scoring函数，经过softmax，则可表示如下：

式子中  表示下一个单词是w在单词库中的概率；  表示当前单词库中所有单词的概率的累和(即“归一化因子“)

一般来说，单词库  的数量是非常巨大的，因此计算“归一化因子“是非常昂贵、耗时的一件事，这也就是 NCE 要解决的问题。

根本方法：通过最大化同一个目标函数来估计模型参数  和归一化常数。

核心思想：通过学习数据分布样本和噪声分布样本之间的区别，从而发现数据中的一些特性。

更具体来说，NCE 将问题转换成了一个二分类问题，分类器能够对数据样本和噪声样本进行二分类。

现在假设一个特定上下文 c 的数据分布为  ，称从它里面取出的样本为正样本，令其类别  ；而另一个与 c 无关的噪声分布为，称从里面取出的样本为负样本，令其类别为 。

假设现在取出了 个正样本和  个负样本。

我们得到下面这些概率:

所以根据贝叶斯公式，可以计算后验概率：

设  ：

同理

好了，现在就是求（3）式中  的问题了。

NCE将问题进行了转换，引入了噪声分布：

• 将  作为一个参数  来进行估计，相当于引进了一个新参数。

• 由[4]中实验证明，我们将  固定为 1 对每个c仍是有效的。

所以(3)可化简为

所以(4)，(5)，(6)联合，可得 

现在我们有了参数为  的二元分类问题。标签  可近似为伯努利分布，那么很容易写出条件对数似然  。

实际上在它前面加上负号后，也就等价于交叉熵损失函数：

NCE 的目标函数还需要在(9)式的基础上除以正样本的数量  ，即

根据大数定律，上式可化为：

要最大化上述对数似然函数，也就是最大化如下目标函数：

可以看到实际上这个比例k对我们的 NCE 优化是有影响的。

根据[5]的结论：对于设置的噪声分布 ，当负样本和正样本数量之比  越大，那么NCE 对于噪声分布的依赖程度也就越小。换句话说，尽可能增大比值  。也许这也就是大家都默认将正样本数量设置为 1 的原因：正样本至少取要 1 个，所以最大化比值k，也就是尽可能取更多负样本的同时，将正样本数量取最小值 1。

另外，如果我们希望目标函数不是只针对一个特定的上下文  ，而是使不同的上下文可以共享参数，也就是设置一批上下文的全局目标函数：

总结：

1. 从上下文  中取出单词作为正样本，从噪声分布中取出单词作为负样本，正负样本数量比为 
   

2. 训练一个二分类器，通过一个类似于交叉熵损失函数的目标函数进行训练（如果取正样本数量为 1，那么(9)与(10) 式等价，NCE 目标函数就等价于交叉熵损失函数）。
   

原理

上面虽然推导了那么多公式，但实际只是按照 NCE 的思想进行问题的转换，那么这样做究竟是否正确呢？

我们再看回(12)式，我们对它关于  进行求导:

分布对上面的两项分别进行求导：

(15)，(16)代入(14)中，可得：

如果负样本与正样本比例  ，那么：

可以看到，(18)与(2)中 MLE 对数似然函数梯度是等价的，也就是说我们通过 NCE 转换后的优化目标，本质上就是对极大似然估计方法的一种近似，并且随着负样本和正样本数量比k的增大，这种近似越精确，这也解释了为什么作者建议我们将 k 设置的越大越好。

InfoNCE Loss

结论

推导

【建议看完CPC介绍再来看这里】

InfoNCE 是在[6]CPC中提出的。CPC(对比预测编码) 就是一种通过无监督任务来学习高维数据的特征表示，而通常采取的无监督策略就是根据上下文预测未来或者缺失的信息。

原文引入了互信息的思想，认为我们可以通过最大化当前上下文  和下  个时刻的数据  之间的互信息来构建预测任务，互信息的定义表示如下：

我们无法知道  和  之间的联合分布  ，因此要最大化  ，就需要最大化  。

把这个比例定义为密度比，那么，分子  就相当于  ，是想得到的目标函数；分母就相  当于  ，是用来进行对比的噪声。

因此，我们就可以根据NCE中提供的思路，将问题转换为一个二分类的问题，更具体来解释：

1. 从条件中取出数据称为“正样本”，它是根据上下文  所做出的预测数据，将它和这个上下文一起组成“正样本对”，类别标签设为 1。
   

2. 将从中取出的样本称为“负样本”，它是与当前上下文没有必然关系的随机数据，将它和这个上下文 一起组成“负样本对”，类别标签设为 0。
   

3. 正样本也就是与  间隔固定步长  的数据，根据 NCE 中说明的设定，正样本选取 1 个；
   因为在 NCE 中证明了噪声分布与数据分布越接近越好，所以负样本就直接在当前序列中随机选取（只要不是那一个正样本就行），负样本数量越多越好。
   

所以要做的就是训练一个 logistics 分类模型，来区分这两个正负样本对。问题转换后，训练的模型能够“成功分辨出每个正负样本的能力”就等价于“根据  预测  的能力”。

根据 NCE 中的设置，现在假设给出一组大小为N的 ，其中包含1个从  中取的正样本和N-1个  中取得负样本。

设  是正样本，上下文表示  之前的数据，那么能够正确的同时找到那一个正样本和和 N-1 个负样本的情况可以写成如下形式：

【相当于把t+k的位置mask】

即

我们最大化上面这个式子，即最大化模型“成功分辨出每个正负样本的能力”，也就是最大化我们定义的密度比，也就是最大化  和  的互信息。

根据(3)式：

在上式中，我们知道  是一个scoring函数，CPC 文章中用余弦相似度来量化，定义为 

那么(21)式可化为：

对比(20)和(22)，我们可以发现：

现在我们的优化目标就是使(20)或(22) 式的结果最大，所以可以写出对应形式的交叉熵损失如下：

即

上式就是最终得到的 InfoNCE 损失函数了，并且最小化 InfoNCE，也就等价于最大化 和  的互信息的下限，从而做到了我们所要求的最大化  。

原理

为什么最小化InfoNCE等价于最大化 和  的互信息的下限？

证明如下：

对于(20)式，我们可以代入(24)，并且，已知，除了  其余均是负样本：

 如果正负样本距离能够拉的足够远，那么所有的负样本期望都会在margin  附近，且近乎相等。那么，就有下列式子成立：

代入(19)式即可算出互信息的下限：

在使用 InfoNCE 时把它当作一个对比损失，那么分子上的 表示正样本对， 分母上的  表示负样本对，我们只要构建好正负样本对，然后利用 InfoNCE 的优化过程，就可以使正样本对之间的互信息最大，使负样本对之间的互信息最小了：

参考：

论文

[1]Raia Hadsell, Sumit Chopra, and Yann LeCun. 2006. Dimensionality reduction by learning an invariant mapping. In CVPR.

[2]Schroff, F. Kalenichenko, D.and Philbin, J. 2015. Facenet: A unified embedding for face recognition and clustering. In Proc. IEEE Conf. Comput. Vis. Pattern Recognit.

[3] Michael Gutmann and Aapo Hyvärinen. 2010. Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proc. AISTATS.

[4]Andriy Mnih and Y ee Whye Teh. 2012. A fast and simple algorithm for training neural probabilistic language models. In Proc. ICML.

[5]Gutmann, M.U. and Hyv¨ arinen, A. Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics. Journal of Machine Learning Research, 13:307–361, 2012.

[6]Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018.

[7]Cheng, Pengyu , et al. "CLUB: A Contrastive Log-ratio Upper Bound of Mutual Information." (2020).

博客参考

[a]ankeshanand.com/blog/20

[b]Lethe：Noise Contrastive Estimation 前世今生——从 NCE 到 InfoNCE

[c]得未曾有：理解Contrastive Predictive Coding和NCE Loss

[d]hahakity：Moco 文章阅读笔记

[e]极光无限：无监督学习之对比学习

[f]BBuf：【损失函数合集】Contrastive Loss 和 Triplet Loss

[g]宋文乐：深度学习中的互信息量上下界估计

[h]军火交易商：详解对比损失（contrastive loss）与交叉熵损失（cross-entropy）的关系

[i]PaperWeekly：深度学习中的互信息：无监督提取特征

[j]自监督、半监督和有监督全涵盖，四篇论文遍历对比学习的研究进展

---