大数据分析-利用k-means聚类分析对客户种类进行分析_kmeans聚类算法预测消费产品模型

一. 选题的背景

     在当今社会，大数据已经成为了企业决策的重要依据，我们可以通过对客户进行细分分析，企业可以更好的了解客户的需求和行为，从而制定出更加精准的营销策略，从而提高产品的竞争力，更加要达到通过对客户的数据分析，从而找出不同客户群体的特征和需求，为企业提供有针对性的营销建议。从社会，经济，技术，数据来源等方面来看，随着互联网和移动互联网的快速发展，企业和个人产生的数据量呈现井喷式的增长，这些数据为大数据分析提供了丰富的数据来源，同时大数据技术也有了更加广泛的应用。

二. 大数据分析设计方案

 2.1 本数据集的数据内容与数据特征分析

首先给出本次项目所要使用的数据集链接： 

           kaggle:https://www.kaggle.com/datasets/govindkrishnadas/segment/data

本数据集的数据包括 客户ID,  性别， 客户年龄， 客户年收入， 客户的消费习惯。

1. 客户ID: 代表唯一标识客户的整数；

2. 客户的性别： 区分男客户和女客户， 使得相关数据更加的完整；

3. 客户的年龄： 客户的出生年份，表示客户的年龄；

4. 客户的年收入： 客户的年度收入， 表示客户的消费能力；

5. 客户的消费习惯： 客户的购买行为和偏好， 包括所购买商品的类别，购买次数，购买金额。

对于数据特征的分析主要包括以下几个方面：

1. 描述性统计分析： 对客户年龄，客户年收入等数值性特征进行描述性的统计分析，了解数据的基本情况；

2. 分类特征分析： 对客户的消费习惯等特征进行分析，从而找出不同类别的特征分布情况；

3. 关联规则挖掘： 分析不同特征之间的关联关系，例如年龄和消费习惯等；

4. 聚类分析： 通过聚类算法将客户化分为不同的群体，从而找出每个特征的特征和需求。

2.2 数据分析的方案概述

1. 数据预处理： 对原始数据进行清洗，缺失值处理，异常值处理等，为后续的数据分析做好准别

2. 描述性统计分析： 利用Python的pandas库进行描述性统计分析，例如计算平均数，中位数，等

3. 聚类分析： 使用k-means算法或者层次聚类算法进行聚类分析，从而将样本中的客户划分为不同的群体

三. 数据分析的具体步骤

3.1 数据源

数据来自：    kaggle:https://www.kaggle.com/datasets/govindkrishnadas/segment/data

3.2 数据清洗

导入库：

#导入所需库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
plt.style.use('fivethirtyeight')
from sklearn.cluster import KMeans
import plotly as py
import plotly.graph_objects as go
import warnings
import os
warnings.filterwarnings('ignore')

读取数据并显示出数据集的前五行：

#读取数据集并显示前5行
df=pd.read_csv(r'C:\Users\Lenovo\Desktop\杂类文件夹\人工智能课程设计\k-means聚类分析\k-means\database\Segmentation_dataset.csv')
df.head()

将数据集下载好之后放置到项目的同级目录下，执行下面的相关命令之后运行：

python main.py

显示出的数据前五行内容如下：

 #   Column                  Non-Null Count  Dtype
---  ------                  --------------  -----
 0   CustomerID              1599 non-null   int64
 1   Gender                  1599 non-null   object
 2   Age                     1599 non-null   int64
 3   Annual Income (k$)      1599 non-null   int64
 4   Spending Score (1-100)  1599 non-null   int64

从数据的基本情况可以看出数据的主要评价指标：

3.3 数据分析与可视化

查看数据分布情况：

#查看数据分布
sns.pairplot(df)

运行之后就可以系那是出数据的结果：

单独查看数据直方图：

#单独查看直方图
plt.figure(1,figsize=(12,6))
n=0
for x in ['Age','Annual Income (k$)','Spending Score (1-100)']:
    n+=1
    plt.subplot(1,3,n)
    plt.subplots_adjust(hspace=0.5,wspace=0.5)
    sns.distplot(df[x],bins=20)
plt.show()

运行之后显示的结果如下所示： 

 每一个柱状图显示出了不同年龄段的人口密度，第二个柱状图显示了不同年龄段的之处得分，第三个柱状图显示了不同年龄段的平均收入，从图中可以看出，随着年龄的增长，人口密度逐渐减少，而之处得分与平均年收入呈现不同的趋势：

样本数据中的性别比例：

#样本数据中的性别比
#计算每个性别的数量
df_gender_c = df['Gender'].value_counts()
#定义了标签、颜色等
p_lables = ['Female', 'Male']
p_color = ['lightcoral', 'lightskyblue']
p_explode = [0, 0.03]
# 绘图
#创建一个10x10的图形窗口
plt.figure(1,figsize=(10,10))
plt.pie(df_gender_c, labels=p_lables, colors=p_color, explode=p_explode, shadow=True, autopct='%.2f%%')
plt.title('Sex Ratio',fontsize=20)
plt.axis('off')
plt.legend(fontsize=14)
plt.legend()
plt.show()

 如下所示：

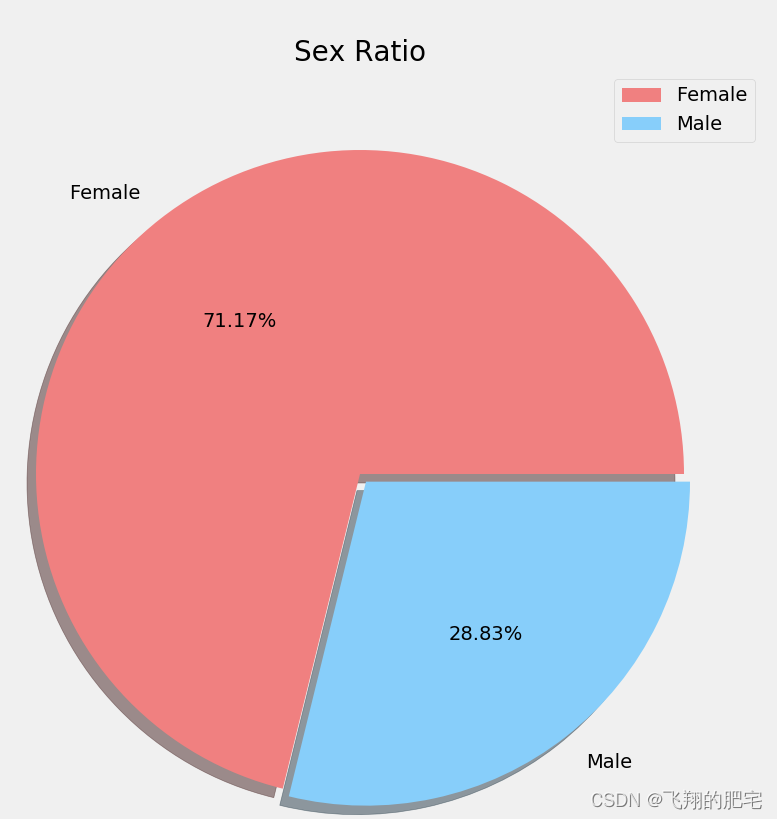
 从图中可以看出，女性人口占比为71%，男性人口占比，有助于了解人口结构中的性别差异：

年龄与年收入的关系：

#显示年龄与年收入的关系
# 导入matplotlib.pyplot库，用于绘制图形
import matplotlib.pyplot as plt
# 设置字体为SimHei，支持中文显示
plt.rcParams['font.sans-serif'] = [u'SimHei']
# 设置负号正常显示
plt.rcParams['axes.unicode_minus'] = False
# 创建一个12x6英寸的图形窗口
plt.figure(1,figsize=(12,6))
# 遍历性别列表，分别绘制男性和女性的散点图
for gender in ['Male','Female']:
    # 使用scatter函数绘制散点图，x轴为年龄，y轴为年收入，数据来源为df中性别为当前性别的数据
    plt.scatter(x='Age',y='Annual Income (k$)',data=df[df['Gender']==gender],
               s=100,alpha=0.5,label=gender)
# 设置x轴标签为“Age”，y轴标签为“Annual Income (k$)”
plt.xlabel('Age'),plt.ylabel('Annual Income (k$)')
# 设置图形标题为“不同性别在年龄与年收入之间的关系”
plt.title('不同性别在年龄与年收入之间的关系')
# 显示图例
plt.legend()
# 显示图形
plt.show()

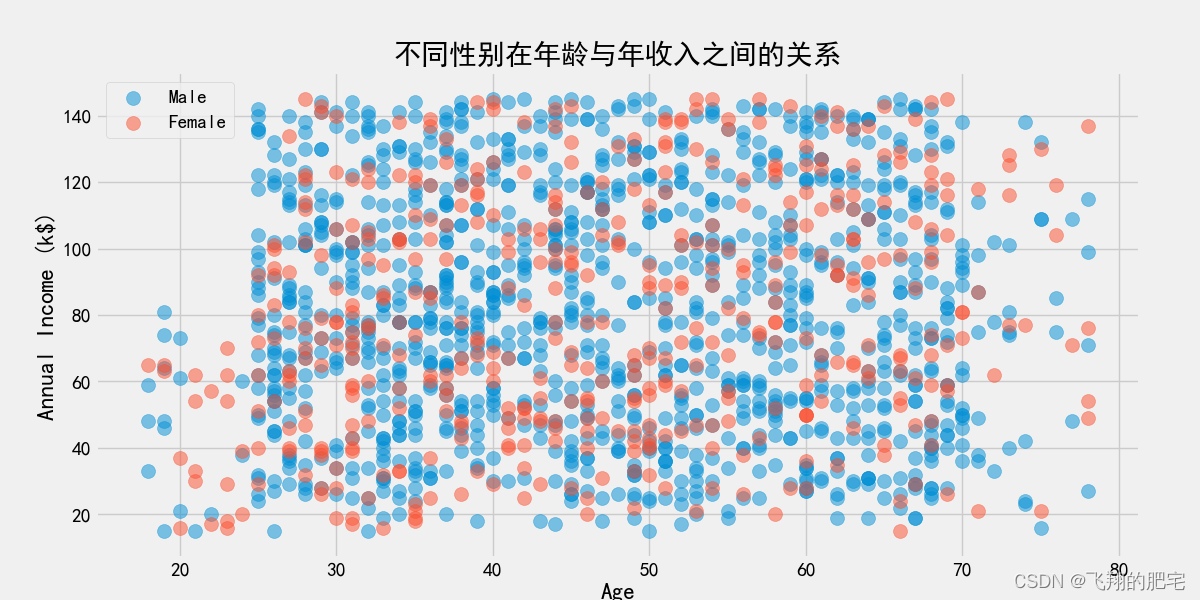
从图中可以看出，不同的性别在年龄与年收入之间存在差异，这就意味着不同性别在相同的年龄段年收入水平存在差异，不同性别在不同的年龄段存在差异 

年龄与消费的分之间的关系：

#不同性别在年龄与年收入之间的关系
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False
 
plt.figure(1,figsize=(12,6))
for gender in ['Male','Female']:
    plt.scatter(x='Age',y='Spending Score (1-100)',data=df[df['Gender']==gender],
               s=100,alpha=0.5,label=gender)
plt.xlabel('Age'),plt.ylabel('Spending Score (1-100)')
plt.title('不同性别在年龄与消费得分之间的关系')
plt.legend()
plt.show()
 
#不同性别在年收入与消费得分之间的关系
plt.figure(1,figsize=(12,6))
for gender in ['Male','Female']:
    plt.scatter(x='Annual Income (k$)',y='Spending Score (1-100)',data=df[df['Gender']==gender],
               s=100,alpha=0.5,label=gender)
plt.xlabel('Annual Income (k$)'),plt.ylabel('Spending Score (1-100)')
plt.title('不同性别在年收入与消费得分之间的关系')
plt.legend()
plt.show()

 从图中可以看出，男性的消费得分普遍偏高，而女性则相对较低，随着年龄的增长，消费的分存在一定的波动，但总体趋势是男性在年轻时消费的分较高，而女性在年长是消费得分较低。

年龄与消费的分与年收入之间的分布：

# 创建一个1行3列的图形，大小为12x6英寸
plt.figure(1,figsize=(12,6))
# 初始化计数器n
n=0
# 遍历三个类别（年龄、年收入和消费得分）
for cloname in ['Age','Annual Income (k$)','Spending Score (1-100)']:
    # 增加计数器n的值
    n+=1
    # 创建第n个子图
    plt.subplot(1,3,n)
    # 调整子图之间的水平间距和垂直间距
    plt.subplots_adjust(hspace=0.5,wspace=0.5)
    # 使用箱线图展示不同性别在当前类别的数据分布情况
    sns.boxenplot(x=cloname,y='Gender',data=df,palette='vlag')
    # 使用散点图展示不同性别在当前类别的数据分布情况
    sns.swarmplot(x=cloname,y='Gender',data=df,alpha=0.5)
    # 如果当前子图是第一个子图，则不显示y轴标签
    plt.ylabel('' if n==1 else '')
    # 如果当前子图是第三个子图，则不显示标题
    plt.title('不同性别的数据分布情况' if n==2 else '')
# 显示图形
plt.show()

最后显示的结果如下：

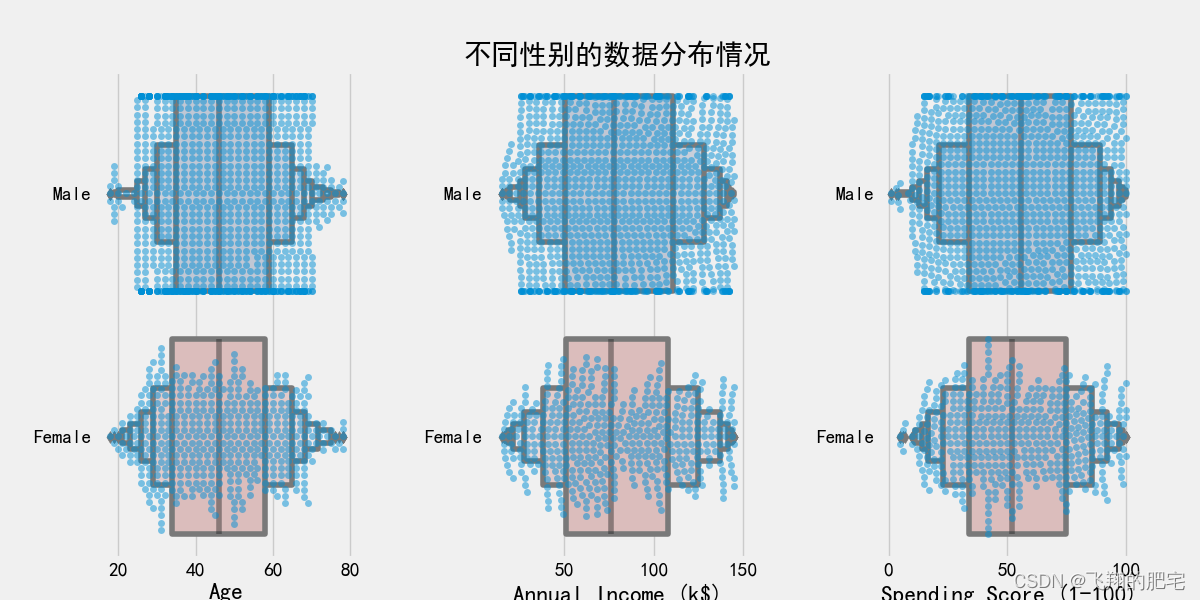
这张图展示了不同性别在年龄，年收入和之处得分之间的变化情况，从图中可以看出，男性在相关指标上分布较为集中，二女性则呈现分散的趋势，可以移位这男性在这些方面表现的相对稳定，二女性则存在一定的波动。 

3.4 使用k-means聚类进行分析

根据年龄和消费得分进行细分：

#使用k-means进行聚类分析，根据年龄和消费得分进行细分
# 从数据框df中提取'Age'和'Spending Score (1-100)'两列的数据，并将其转换为numpy数组x1
x1 = df[['Age', 'Spending Score (1-100)']].iloc[:, :].values
 
# 导入KMeans类
from sklearn.cluster import KMeans
# 初始化一个空列表inertia，用于存储每次迭代的inertia值
inertia = []
# 循环尝试不同的聚类数量（从1到10）
for i in range(1, 11):
    # 创建KMeans对象，设置聚类数量、初始化方法、最大迭代次数、初始运行次数和随机种子
    km = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
    # 使用KMeans对象对数据进行拟合
    km.fit(x1)
    # 将当前迭代的inertia值添加到inertia列表中
    inertia.append(km.inertia_)
 
# 创建一个大小为12x6的图形窗口
plt.figure(1, figsize=(12, 6))
# 绘制inertia值随聚类数量变化的曲线图
plt.plot(range(1, 11), inertia)
# 设置图形标题和坐标轴标签
plt.title('The Ebow Method', fontsize=20)
plt.xlabel('Number of Clusters')
plt.ylabel('inertia')
# 显示图形
plt.show()

该图显示出了列表指标随着聚类数量变化的折线关系图，能够反映聚类所产生的关系 ，

利用The Elbow Method手肘法则由图可知最佳聚类个数是1.0：

# 创建KMeans对象，设置聚类数量为4，初始化方法为'k-means++'，最大迭代次数为500，初始运行次数为10，随机种子为0
km = KMeans(n_clusters=4, init='k-means++', max_iter=500, n_init=10, random_state=0)
# 使用KMeans模型对数据x1进行拟合，并预测每个样本所属的簇
y_means = km.fit_predict(x1)
# 创建一个大小为16x8的图形窗口
plt.figure(1, figsize=(16, 8))
# 绘制属于簇0的样本点，颜色为蓝色，标签为'1'，透明度为0.6
plt.scatter(x1[y_means == 0, 0], x1[y_means == 0, 1], s=200, c='blue', label='1', alpha=0.6)
# 绘制属于簇1的样本点，颜色为橙色，标签为'2'，透明度为0.6
plt.scatter(x1[y_means == 1, 0], x1[y_means == 1, 1], s=200, c='orange', label='2', alpha=0.6)
# 绘制属于簇2的样本点，颜色为粉色，标签为'3'，透明度为0.6
plt.scatter(x1[y_means == 2, 0], x1[y_means == 2, 1], s=200, c='pink', label='3', alpha=0.6)
# 绘制属于簇3的样本点，颜色为紫色，标签为'4'，透明度为0.6
plt.scatter(x1[y_means == 3, 0], x1[y_means == 3, 1], s=200, c='purple', label='4', alpha=0.6)
# 绘制聚类中心点，颜色为红色，标签为'5'，透明度为0.6
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=200, c='red', label='5', alpha=0.6)
# 设置y轴标签为'Spending Score (1-100)'，x轴标签为'Age'
plt.ylabel('Spending Score (1-100)'), plt.xlabel('Age')
# 显示图例
plt.legend()
# 显示图形
plt.show()

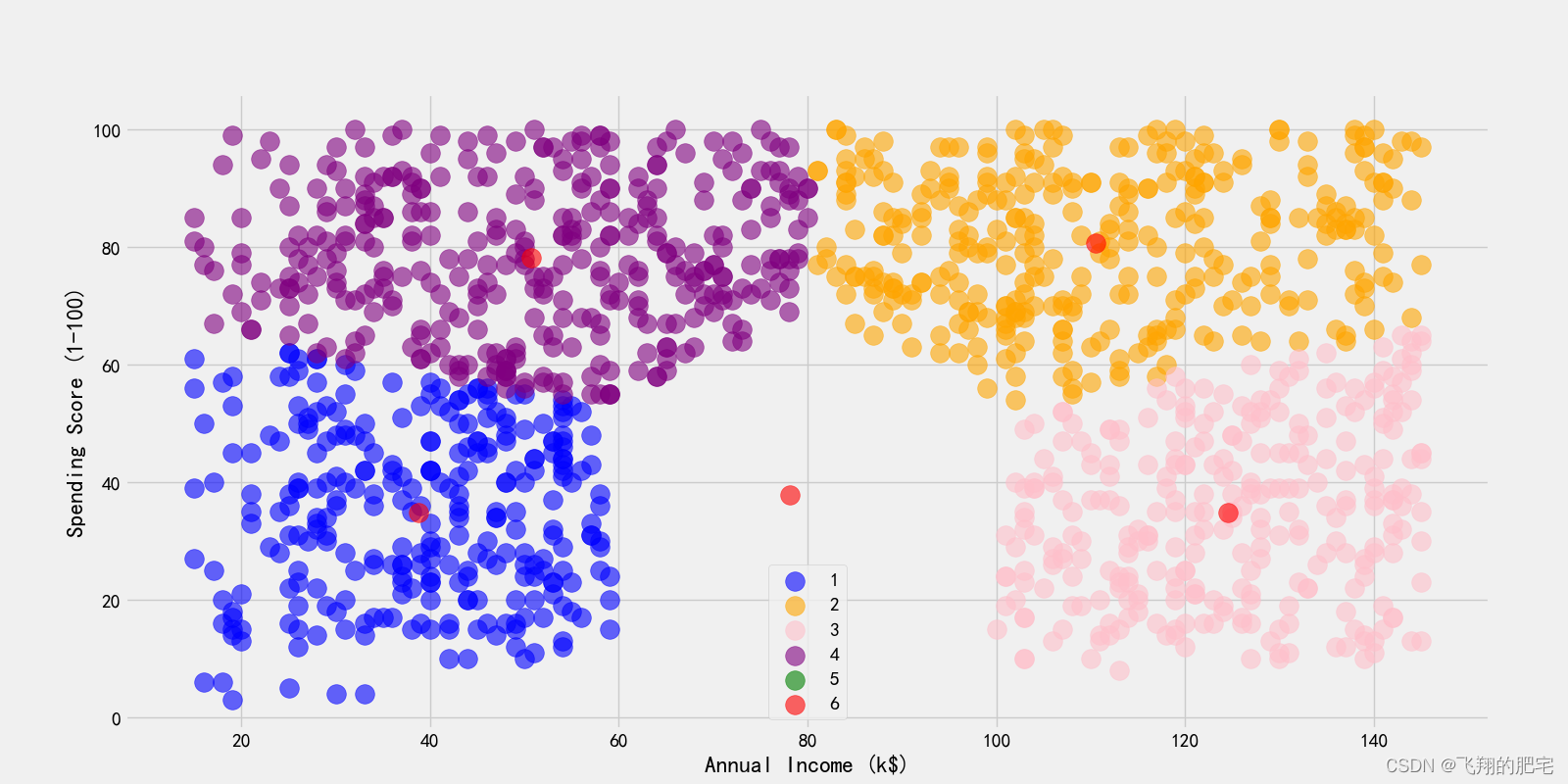
 由运行的记过可以蓝色代表第一个簇，橙色代表第二个簇，紫色代表第三个簇，红色还可以用来表示聚类中心，可以了解不同颜色点在年龄和消费得分上的分布情况，以及他们所属的簇和聚类中心。

在此利用KMeans算法对数据进行聚类，并绘制3D散点图来展示聚类效果 ：

#使用KMeans算法对数据进行聚类，并绘制3D散点图展示聚类结果
# 创建KMeans算法实例，设置聚类数量为6，初始化方法为'k-means++'，运行次数为10，最大迭代次数为300，容差为0.0001，随机种子为100，使用'elkan'算法
algorithm = (KMeans(n_clusters=6, init='k-means++', n_init=10, max_iter=300, tol=0.0001, random_state=100, algorithm='elkan'))
# 使用算法对数据x3进行拟合
algorithm.fit(x3)
# 获取聚类标签
labels = algorithm.labels_
# 获取聚类中心
centroids = algorithm.cluster_centers_
 
# 将聚类标签添加到原始数据框df中
df['label'] = labels
# 创建3D散点图，x轴为年龄，y轴为消费得分（1-100），z轴为年收入（k$），根据聚类标签设置颜色和大小，同时设置线条颜色和宽度，透明度为0.8
trace1 = go.Scatter3d(
    x=df['Age'],
    y=df['Spending Score (1-100)'],
    z=df['Annual Income (k$)'],
    mode='markers',
    marker=dict(
        color=df['label'],
        size=5,
        line=dict(
            color=df['label'],
            width=5
        ),
        opacity=0.8
    )
)
# 定义绘图布局，设置高度、宽度、标题和坐标轴标题
data = [trace1]
layout = go.Layout(
    height=1000,
    width=1000,
    title='Clusters!',
    scene=dict(
        xaxis=dict(title='Age'),
        yaxis=dict(title='Spending Score (1-100)'),
        zaxis=dict(title='Annual Income (k$)')
    )
)
# 创建绘图对象，传入数据和布局
fig = go.Figure(data=data, layout=layout)
# 离线显示绘图结果
py.offline.iplot(fig)

聚类的结果如下

图中的每个彩色小点代表一个观察值，他们在x轴与y轴上的位置分别表示年龄年收入，在z轴上的位置代表消费的分，通过观察这些小点的密度和大小，我们可以了解到数据在这个上面的三维分布情况 。

轮廓系数：

# 轮廓系数
import sklearn.metrics
score = []
for i in range(2,10):
    model = KMeans(n_clusters=i).fit(x2)
    score.append(silhouette_score(x2, model.labels_, metric='euclidean'))
plt.plot(range(2,10),score)
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.show()
kmeans = KMeans( n_clusters = 6, init='k-means++')
kmeans.fit(x1)
print(silhouette_score(x2, kmeans.labels_, metric='euclidean'))
 

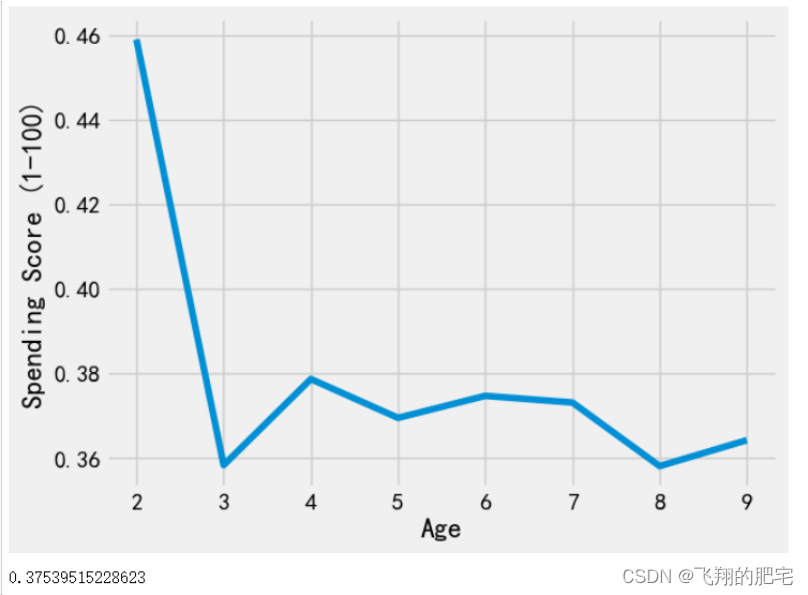
由图可知年龄与消费的分之间的轮廓系数为0.37，接近于0可以看出样本差距不大聚类效果一般

四. 完成的程序代码 

#Time:    2024 1.9
#autor:   GaoShun
#k-means:  main.py
#database: https://www.kaggle.com/datasets/govindkrishnadas/segment/data
#导入库函数
 
import matplotlib.pyplot as plt
# 导入库
import pandas as pd
import seaborn as sns
plt.style.use('fivethirtyeight')
import plotly as py
import plotly.graph_objects as go
import warnings
warnings.filterwarnings('ignore')
import os
 
#读取数据集并显示前5行
df=pd.read_csv(r'C:\Users\Lenovo\Desktop\杂类文件夹\人工智能课程设计\k-means聚类分析\k-means\database\Segmentation_dataset.csv')
df.head()
 
df.shape
 
df.info()
 
df.dtypes
 
#查看各列缺失值数量
df.isnull().sum()
 
df.describe()
 
#查看数据分布
sns.pairplot(df)
 
#单独查看直方图
plt.figure(1,figsize=(12,6))
n=0
for x in ['Age','Annual Income (k$)','Spending Score (1-100)']:
    n+=1
    plt.subplot(1,3,n)
    plt.subplots_adjust(hspace=0.5,wspace=0.5)
    sns.distplot(df[x],bins=20)
plt.show()
 
#样本数据中的性别比
#计算每个性别的数量
df_gender_c = df['Gender'].value_counts()
#定义了标签、颜色等
p_lables = ['Female', 'Male']
p_color = ['lightcoral', 'lightskyblue']
p_explode = [0, 0.03]
# 绘图
#创建一个10x10的图形窗口
plt.figure(1,figsize=(10,10))
plt.pie(df_gender_c, labels=p_lables, colors=p_color, explode=p_explode, shadow=True, autopct='%.2f%%')
plt.title('Sex Ratio',fontsize=20)
plt.axis('off')
plt.legend(fontsize=14)
plt.legend()
plt.show()
 
#显示年龄与年收入的关系
# 导入matplotlib.pyplot库，用于绘制图形
import matplotlib.pyplot as plt
# 设置字体为SimHei，支持中文显示
plt.rcParams['font.sans-serif'] = [u'SimHei']
# 设置负号正常显示
plt.rcParams['axes.unicode_minus'] = False
# 创建一个12x6英寸的图形窗口
plt.figure(1,figsize=(12,6))
# 遍历性别列表，分别绘制男性和女性的散点图
for gender in ['Male','Female']:
    # 使用scatter函数绘制散点图，x轴为年龄，y轴为年收入，数据来源为df中性别为当前性别的数据
    plt.scatter(x='Age',y='Annual Income (k$)',data=df[df['Gender']==gender],
               s=100,alpha=0.5,label=gender)
# 设置x轴标签为“Age”，y轴标签为“Annual Income (k$)”
plt.xlabel('Age'),plt.ylabel('Annual Income (k$)')
# 设置图形标题为“不同性别在年龄与年收入之间的关系”
plt.title('不同性别在年龄与年收入之间的关系')
# 显示图例
plt.legend()
# 显示图形
plt.show()
 
#不同性别在年龄与年收入之间的关系
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False
 
plt.figure(1,figsize=(12,6))
for gender in ['Male','Female']:
    plt.scatter(x='Age',y='Spending Score (1-100)',data=df[df['Gender']==gender],
               s=100,alpha=0.5,label=gender)
plt.xlabel('Age'),plt.ylabel('Spending Score (1-100)')
plt.title('不同性别在年龄与消费得分之间的关系')
plt.legend()
plt.show()
 
#不同性别在年收入与消费得分之间的关系
plt.figure(1,figsize=(12,6))
for gender in ['Male','Female']:
    plt.scatter(x='Annual Income (k$)',y='Spending Score (1-100)',data=df[df['Gender']==gender],
               s=100,alpha=0.5,label=gender)
plt.xlabel('Annual Income (k$)'),plt.ylabel('Spending Score (1-100)')
plt.title('不同性别在年收入与消费得分之间的关系')
plt.legend()
plt.show()
 
# 创建一个1行3列的图形，大小为12x6英寸
plt.figure(1,figsize=(12,6))
# 初始化计数器n
n=0
# 遍历三个类别（年龄、年收入和消费得分）
for cloname in ['Age','Annual Income (k$)','Spending Score (1-100)']:
    # 增加计数器n的值
    n+=1
    # 创建第n个子图
    plt.subplot(1,3,n)
    # 调整子图之间的水平间距和垂直间距
    plt.subplots_adjust(hspace=0.5,wspace=0.5)
    # 使用箱线图展示不同性别在当前类别的数据分布情况
    sns.boxenplot(x=cloname,y='Gender',data=df,palette='vlag')
    # 使用散点图展示不同性别在当前类别的数据分布情况
    sns.swarmplot(x=cloname,y='Gender',data=df,alpha=0.5)
    # 如果当前子图是第一个子图，则不显示y轴标签
    plt.ylabel('' if n==1 else '')
    # 如果当前子图是第三个子图，则不显示标题
    plt.title('不同性别的数据分布情况' if n==2 else '')
# 显示图形
plt.show()
 
 
#使用k-means进行聚类分析，根据年龄和消费得分进行细分
# 从数据框df中提取'Age'和'Spending Score (1-100)'两列的数据，并将其转换为numpy数组x1
x1 = df[['Age', 'Spending Score (1-100)']].iloc[:, :].values
 
# 导入KMeans类
from sklearn.cluster import KMeans
# 初始化一个空列表inertia，用于存储每次迭代的inertia值
inertia = []
# 循环尝试不同的聚类数量（从1到10）
for i in range(1, 11):
    # 创建KMeans对象，设置聚类数量、初始化方法、最大迭代次数、初始运行次数和随机种子
    km = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
    # 使用KMeans对象对数据进行拟合
    km.fit(x1)
    # 将当前迭代的inertia值添加到inertia列表中
    inertia.append(km.inertia_)
 
# 创建一个大小为12x6的图形窗口
plt.figure(1, figsize=(12, 6))
# 绘制inertia值随聚类数量变化的曲线图
plt.plot(range(1, 11), inertia)
# 设置图形标题和坐标轴标签
plt.title('The Ebow Method', fontsize=20)
plt.xlabel('Number of Clusters')
plt.ylabel('inertia')
# 显示图形
plt.show()
 
# 创建KMeans对象，设置聚类数量为4，初始化方法为'k-means++'，最大迭代次数为500，初始运行次数为10，随机种子为0
km = KMeans(n_clusters=4, init='k-means++', max_iter=500, n_init=10, random_state=0)
# 使用KMeans模型对数据x1进行拟合，并预测每个样本所属的簇
y_means = km.fit_predict(x1)
# 创建一个大小为16x8的图形窗口
plt.figure(1, figsize=(16, 8))
# 绘制属于簇0的样本点，颜色为蓝色，标签为'1'，透明度为0.6
plt.scatter(x1[y_means == 0, 0], x1[y_means == 0, 1], s=200, c='blue', label='1', alpha=0.6)
# 绘制属于簇1的样本点，颜色为橙色，标签为'2'，透明度为0.6
plt.scatter(x1[y_means == 1, 0], x1[y_means == 1, 1], s=200, c='orange', label='2', alpha=0.6)
# 绘制属于簇2的样本点，颜色为粉色，标签为'3'，透明度为0.6
plt.scatter(x1[y_means == 2, 0], x1[y_means == 2, 1], s=200, c='pink', label='3', alpha=0.6)
# 绘制属于簇3的样本点，颜色为紫色，标签为'4'，透明度为0.6
plt.scatter(x1[y_means == 3, 0], x1[y_means == 3, 1], s=200, c='purple', label='4', alpha=0.6)
# 绘制聚类中心点，颜色为红色，标签为'5'，透明度为0.6
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=200, c='red', label='5', alpha=0.6)
# 设置y轴标签为'Spending Score (1-100)'，x轴标签为'Age'
plt.ylabel('Spending Score (1-100)'), plt.xlabel('Age')
# 显示图例
plt.legend()
# 显示图形
plt.show()
 
x2=df[['Annual Income (k$)','Spending Score (1-100)']].iloc[:,:].values
import sklearn.cluster
inertia=[]
for i in range(1,11):
    km=KMeans(n_clusters=i,init='k-means++',max_iter=300,n_init=10,random_state=0)
    km.fit(x2)
    inertia.append(km.inertia_)
plt.figure(1,figsize=(12,6))
plt.plot(range(1,11),inertia)
plt.title('The Ebow Method',fontsize=20)
plt.xlabel('Number of Clusters')
plt.ylabel('inertia')
plt.show()
 
km = KMeans(n_clusters = 5, init = 'k-means++', max_iter = 500,n_init = 10,random_state=0)
y_means = km.fit_predict(x2)
plt.figure(1,figsize = (16,8))
plt.scatter(x2[y_means == 0,0],x2[y_means==0,1],s=200,c='blue', label='1', alpha=0.6)
plt.scatter(x2[y_means == 1,0],x2[y_means==1,1],s = 200,c='orange', label='2', alpha=0.6)
plt.scatter(x2[y_means == 2,0],x2[y_means==2,1],s = 200,c='pink', label='3', alpha=0.6)
plt.scatter(x2[y_means == 3,0],x2[y_means==3,1],s = 200,c='purple', label='4', alpha=0.6)
plt.scatter(x2[y_means == 5,0],x2[y_means==5,1],s = 200,c='green', label='5', alpha=0.6)
plt.scatter(km.cluster_centers_[:,0], km.cluster_centers_[:, 1], s = 200,c='red', label='6', alpha=0.6)
plt.ylabel('Spending Score (1-100)'), plt.xlabel('Annual Income (k$)')
plt.legend()
plt.show()
 
x3=df[['Age','Annual Income (k$)','Spending Score (1-100)']].iloc[:,:].values
import sklearn.cluster
inertia=[]
for i in range(1,11):
    km=KMeans(n_clusters=i,init='k-means++',max_iter=300,n_init=10,random_state=0)
    km.fit(x3)
    inertia.append(km.inertia_)
plt.figure(1,figsize=(12,6))
plt.plot(range(1,11),inertia)
plt.title('The Elbow Method',fontsize=20)
plt.xlabel('Number of Clusters')
plt.ylabel('inertia')
plt.show()
 
#使用KMeans算法对数据进行聚类，并绘制3D散点图展示聚类结果
# 创建KMeans算法实例，设置聚类数量为6，初始化方法为'k-means++'，运行次数为10，最大迭代次数为300，容差为0.0001，随机种子为100，使用'elkan'算法
algorithm = (KMeans(n_clusters=6, init='k-means++', n_init=10, max_iter=300, tol=0.0001, random_state=100, algorithm='elkan'))
# 使用算法对数据x3进行拟合
algorithm.fit(x3)
# 获取聚类标签
labels = algorithm.labels_
# 获取聚类中心
centroids = algorithm.cluster_centers_
 
# 将聚类标签添加到原始数据框df中
df['label'] = labels
# 创建3D散点图，x轴为年龄，y轴为消费得分（1-100），z轴为年收入（k$），根据聚类标签设置颜色和大小，同时设置线条颜色和宽度，透明度为0.8
trace1 = go.Scatter3d(
    x=df['Age'],
    y=df['Spending Score (1-100)'],
    z=df['Annual Income (k$)'],
    mode='markers',
    marker=dict(
        color=df['label'],
        size=5,
        line=dict(
            color=df['label'],
            width=5
        ),
        opacity=0.8
    )
)
# 定义绘图布局，设置高度、宽度、标题和坐标轴标题
data = [trace1]
layout = go.Layout(
    height=1000,
    width=1000,
    title='Clusters!',
    scene=dict(
        xaxis=dict(title='Age'),
        yaxis=dict(title='Spending Score (1-100)'),
        zaxis=dict(title='Annual Income (k$)')
    )
)
# 创建绘图对象，传入数据和布局
fig = go.Figure(data=data, layout=layout)
# 离线显示绘图结果
py.offline.iplot(fig)
 
# 导入轮廓系数计算函数
import sklearn.metrics
# 初始化一个空列表，用于存储每个聚类数量对应的轮廓系数
score = []
# 遍历聚类数量从2到9
for i in range(2, 10):
    # 使用KMeans算法对数据x1进行聚类，聚类数量为当前循环的变量i
    model = KMeans(n_clusters=i).fit(x1)
    # 计算聚类结果的轮廓系数，并将结果添加到score列表中
    score.append(silhouette_score(x1, model.labels_, metric='euclidean'))
# 绘制轮廓系数与聚类数量的关系图
plt.plot(range(2, 10), score)
plt.xlabel('Age')
plt.ylabel('Spending Score (1-100)')
plt.show()
# 创建KMeans聚类模型，设置聚类数量为6，初始化方法为'k-means++'
kmeans = KMeans(n_clusters=6, init='k-means++')
# 使用x1数据进行聚类
kmeans.fit(x1)
# 计算x1数据的轮廓系数，使用欧氏距离作为度量标准
print(silhouette_score(x1, kmeans.labels_, metric='euclidean'))
 
# 轮廓系数
import sklearn.metrics
score = []
for i in range(2,10):
    model = KMeans(n_clusters=i).fit(x2)
    score.append(silhouette_score(x2, model.labels_, metric='euclidean'))
plt.plot(range(2,10),score)
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.show()
kmeans = KMeans( n_clusters = 6, init='k-means++')
kmeans.fit(x1)
print(silhouette_score(x2, kmeans.labels_, metric='euclidean'))
 

以下代码仅供参考，可以自行修改参数分别观察聚类的效果，并对效果进行评估。