- 1Android如何防止apk程序被反编译_apk防反编译
- 2大模型时代下的决策范式转变_大模型的统计分析和辅助决策
- 3union all和union的区别以及怎么使用_union all和union的区别用法
- 4oracle的SQL语句中的(+)是干什么用的?
- 5Qt 3D:线框 QML 示例_qml qt3d 画线
- 6SpringBoot升级3.2报错Invalid value type for attribute ‘factoryBeanObjectType‘: java.lang.String_invalid value type for attribute 'factorybeanobjec
- 7七年级上册英语第三单元单词课文翻译_answer是七年级上册第几单元学的
- 8网络编程1 - socket基本函数_socket函数pf
- 9大学生如何选择人生第一份工作
- 10安装g++,在centos上执行yum -y install gcc gcc-c++ libstdc++-devel
Java广联达元素平衡_数据结构—平衡二叉树(AVL树)的原理以及Java代码的完全实现...
赞
踩
平衡二叉树(AVL树),顾名思义,是一颗很“平衡”的树,它的平衡是相对于排序二叉树来说的。为了避免极端情况下二叉搜索树节点分布不均匀,甚至退化为链表,影响查找效率,我们引入了平衡二叉树,即让树的结构看起来尽量“均匀”,左右子树的节点数和层级尽量一样多。
本文详细介绍了平衡二叉树的概念和实现原理,并且提供了Java代码的完全实现。
文章目录
1 平衡二叉树的概述
2 平衡二叉树的实现原理
2.1 单旋转
2.2 双旋转
2.3 总结
3 平衡二叉树的构建
3.1 类架构
3.2 查找的方法
3.3 检查是否平衡的方法
3.4 插入的方法
3.4.1 测试
3.5 查找最大值和最小值
3.6 删除的方法
3.6.1 测试
4 平衡二叉树的总结
1 平衡二叉树的概述
为了避免极端情况下二叉搜索树退化为链表,影响查找效率,我们引入了平衡二叉树,即让树的结构看起来尽量“均匀”,左右子树的节点数和层级尽量一样多。要想学习平衡二叉树并且掌握它,必须要先掌握二叉排序树,如果对二叉搜索树还不太明白的,包括为什么二叉排序树可能退化为链表,可以看看这篇文章:二叉排序树的详解以及Java代码的完全实现。
平衡二叉树,又称AVL树,指的是左子树上的所有节点的值都比根节点的值小,而右子树上的所有节点的值都比根节点的值大,且左子树与右子树的高度差最大为1。因此,平衡二叉树满足所有二叉排序(搜索)树的性质,是在二叉排序树的基础上发展而来的。至于AVL,则是取自两个发明平衡二叉树的俄罗斯科学家的名字:G. M. Adelson-Velsky和E. M. Landis。总的来说它具有如下性质:
它一定是一棵二叉排序树;
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,递归定义。
平衡因子BF(Balance Factor):
我们将二叉树上节点的左子树深度减去右子树深度的值称为,那么平衡二叉树上所有节点的平衡因子只可能是-1、0和1。只要二叉树上有一个节点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。
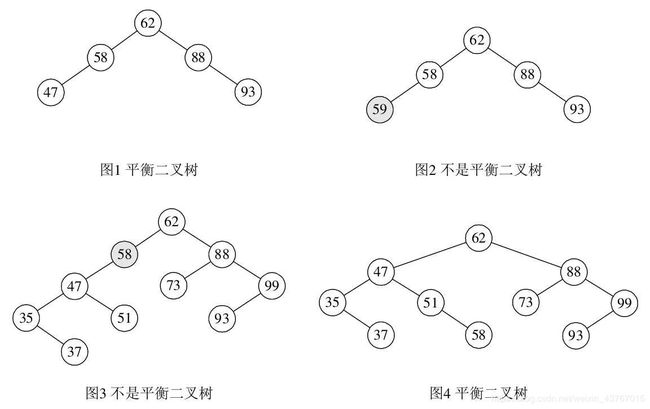
上图中,图一是平衡二叉树,图二的59比58大,却是58的左子树,这是不符合二叉排序树的定义的,图二不是平衡二叉树。图3不是平衡二叉树的原因就在于,节点58的左子树高度为3,而右子树为空,二者差大于了绝对值1,因此它也不是平衡的。而经过适当的调整后的图4,它就符合了定义,因此它是平衡二叉树。
最小不平衡子树:
距离插入、删除节点最近的,且平衡因子的绝对值大于1的节点为根的子树,我们称为最小不平衡子树。下图中当新插入节点37时,距离它最近的平衡因子绝对值超过1的节点是58(即它的左子树高度3减去右子树高度1),所以从58开始以下的子树为最小不平衡子树。
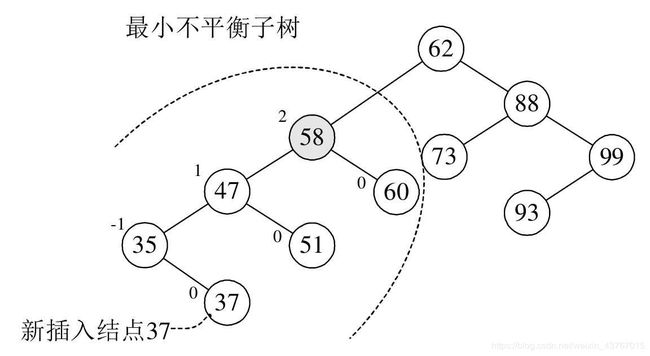
2 平衡二叉树的实现原理
实现原理的核心就是:在插入、删除节点以后,只有那些从插入点到根节点的路径上的节点的平衡可能被改变,因为只有这些节点的子树可能发生变化。当我们沿着这条路径上行到根并更新平衡信息时,尝试找出最小不平衡树。在保持二叉排序树特性的前提下,调整最小不平衡子树中根节点和之点之间的关系,进行相应的旋转(rotation),使之成为新的平衡子树。
先来看看插入的重平衡,因为到后面我们会发现插入和删除进行的重平衡操作基本是一致的。
我们把需要进行平衡(平衡因子绝对值大于1)的节点称为x,由于任意节点最多有两个儿子,因此出现高度不平衡就需要x点的两棵子树的高度差2,而这种不平衡只可能出现在下面四种情况中:
在节点X的左孩子节点的左子树中插入元素,简称LL
在节点X的左孩子节点的右子树中插入元素,简称LR
在节点X的右孩子节点的左子树中插入元素,简称RL
在节点X的右孩子节点的右子树中插入元素,简称RR
其中第1种情况和第4种情况是对称的,被称为发生“外边”的情况,可以通过单旋转来解决,而第2种情况和第3种情况是对称的,被称为发生在“内边”的情况,需要双旋转来解决。
案例:对数组中的元素{3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9}顺序插入并建立一个平衡二叉树。以这个案例为例,来讲解上面4个问题的通用解决办法和单旋转和双旋转的概念。
2.1 单旋转
首先是添加前两个元素“3、2”的时候,可以正常的构建平衡二叉树,到了第3个数“1”时,发现此时根节点“3”的平衡因子变成了2,此时整棵树都成了最小不平衡子树,因此需要调整结构。
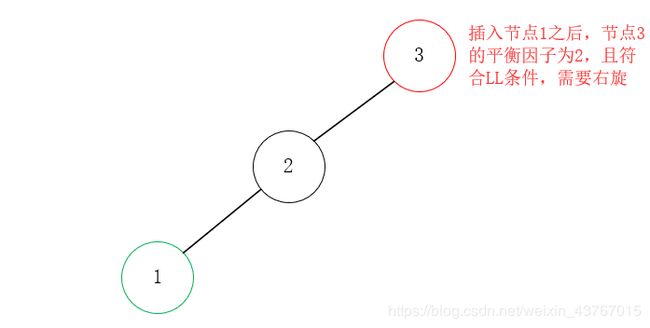
上图中的情况情况符合条件1——LL,因此所采用单旋转来重平衡。此时,我们需要右旋(顺时针旋转)。旋转的目的实际上就是为了降低深度,保持平衡。
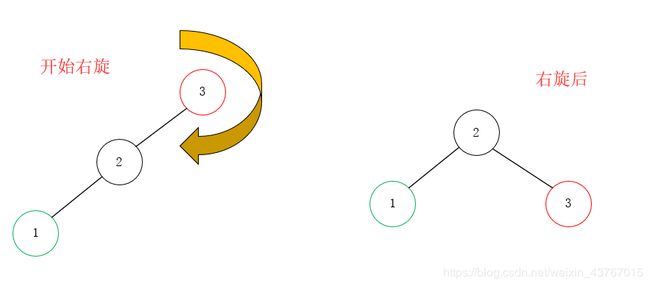
节点3经过右旋后,节点2变成了根节点,节点3变成了2的右子树,此时树节点1的深度降低了一级,整颗树重新回到了平衡。我们把通过一次旋转即可修复平衡的操作叫做单旋转。
平衡因子BF绝对值大于1的节点X称为失衡点,修复一棵被破坏的AVL树时,找到失衡点是很重要的,查找失衡点就是从新插入、删除的节点的位置向上回溯至根节点的过程。
然后我们再增加节点4,平衡因子没有超出限定范围。增加节点5时,节点3的BF值为-2,说明又要旋转了。
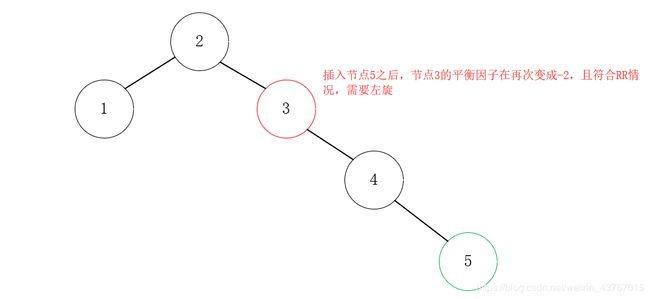
上图中的情况情况符合条件4——RR,需要采用单旋转来重平衡。此时,我们需要左旋(逆时针旋转)。
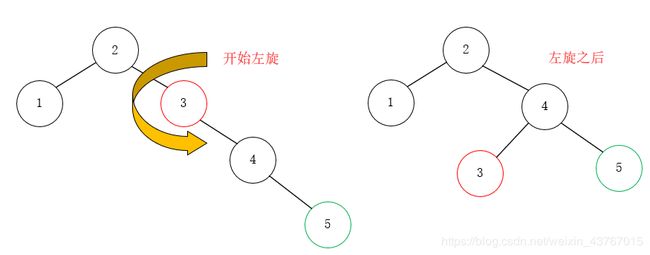
左旋之后,如上图右,树的深度降低了一级,此时整棵树又达到了平衡状态。继续,增加节点6时,发现根节点2的BF值变成了-2,所以我们对根节点进行了左旋。
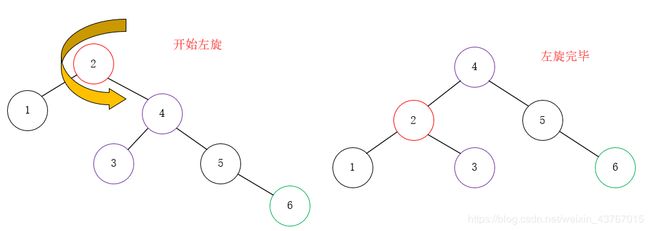
左旋的结果使得节点2成为节点4的左孩子,原本处于2和4之间的节点3是4的左子树,由于旋转后需要满足二叉排序树特性,因此它成了节点2的右子树,因为该子树的每一个关键字都在2-4之间,因此这个变换是成立的。
现在我们来尝试总结出发生情况1和4时的通用解法。首先,情况1和4可以提炼出一个通用模型:
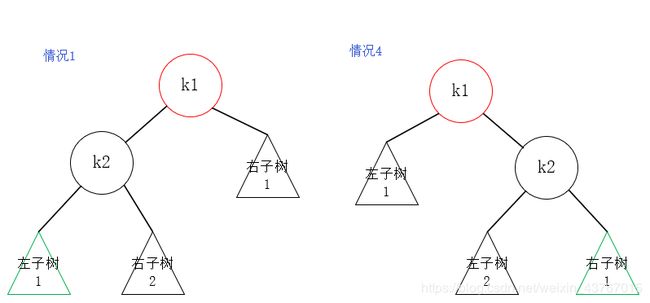
模型中,左边如果要发生不平衡的情况1,那么左子树1的深度肯定比右子树1的深度深2层;右边如果要发生不平衡的情况4,那么左子树1的深度肯定比右子树1的深度浅2层;针对上面情况1和情况4,我们分别使用右旋和左旋,来降低或者升高这两颗子树的深度:
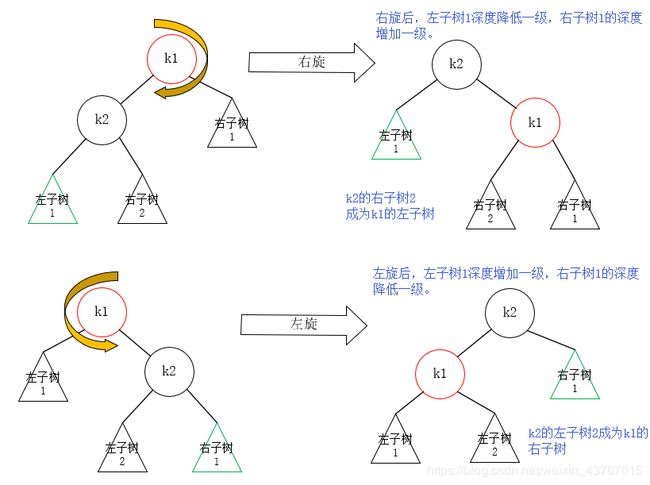
如上图,情况1右旋之后,k2成为根节点,k1成为k2的右子节点,k2的右子树2成为k1的左子树;情况4左旋之后,k2成为根节点,k1成为k2的左子节点,k2的左子树2成为k1的右子树。树重新达到了平衡状态,这就是解决情况1和情况4的通解,并且我们可以发现它们是对称的。
下面增加节点7,这导致节点5的BF变成了-2,且符合情况4,需要左旋,根据上面的通解,采用下面的左旋方法让树重新成为平衡二叉树:
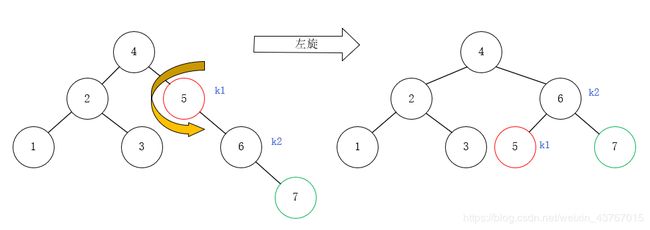
2.2 双旋转
上面的单旋转对于情况2和3是没有用的,因为此时树结构太深,单旋转并不会减低它的深度。此时需要使用双旋转。
当增加节点16时,结构无变化,再增加节点15,此时节点7的BF变成了-2。此时符合情况3:在节点X的右孩子节点的左子树中插入元素,简称RL。如下图:
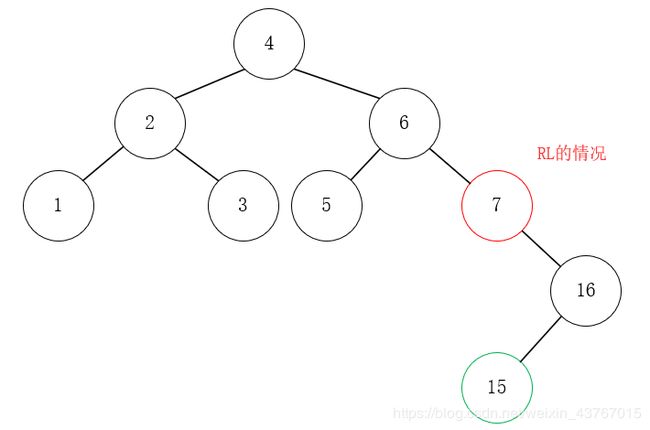
此时简单的左旋无法解决问题:节点9成了10的右孩子,这是不符合二叉排序树的特性的,此时不能简单的左旋。如下图:
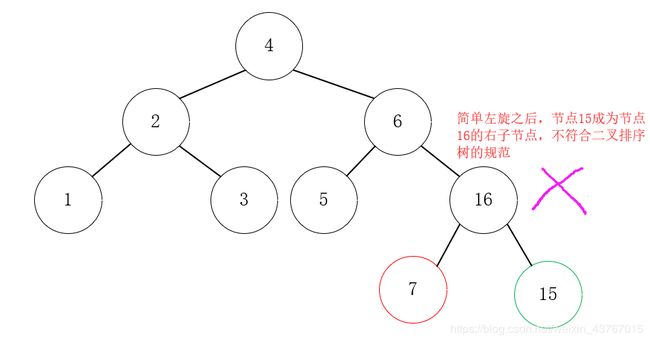
对于这种情况,我们对于关键节点7、16、15先建立一个更广泛的模型:
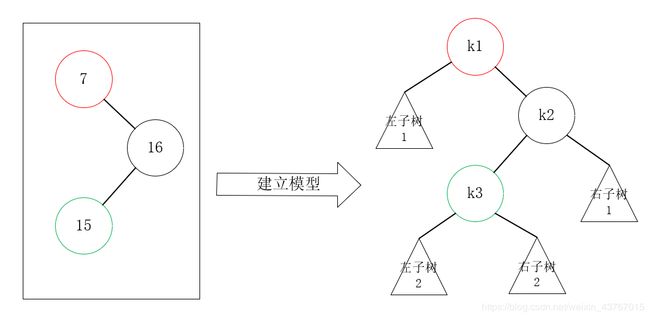
其中7-k1、16-k2、15-k3,并且节点7完全还可以拥有左子树,节点16可以拥有右子树,而节点15则可以拥有左右子树。
要想发生上面k1的BF为-2的情况,需要左子树2或右子树2其中一颗子树的深度比左子树1深两层,或者他们都是空子树,但是我们不知道是具体是什么情况,不过这没关系,在这里我们要求出一个对这个问题通解!
此时为了平衡高度,我们不能将k1当作根节点了,但是左旋——把k2当作根节点也不能解决问题(上面已经证实了),唯一的选择就是:将k3当作新的根节点,并且先使得k2右旋成为k3的右子树,然后k1左旋成为k3的左子树,并且左子树2成为k1的右子树,右子树2成为k2的左子树,这是完全成立的,这就是情况3的通解。 最终,右-左双旋结果如下:
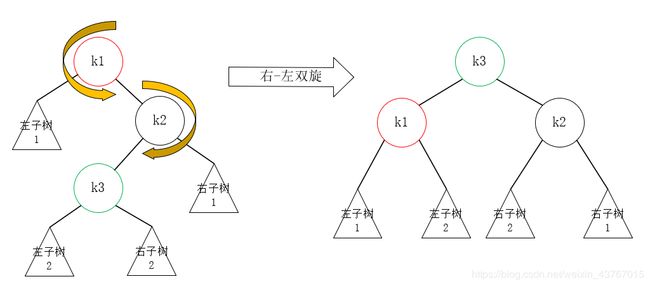
我们可以看到,无论是具体发生了什么情况(左子树2或右子树2其中一颗子树的深度比左子树1深两层,或者他们都是空子树),左-右双旋转换为上右图的形状之后,左子树2或右子树2都会被削减一层深度,而左子树1会被增加一层深度,这棵树始终都是一颗平衡二叉树。
实际上,右-左双旋,分开旋转的过程模型如下:
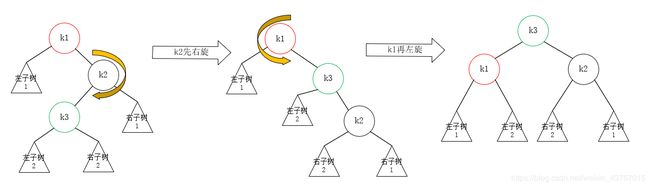
回到案例,案例中左子树2、右子树2、左子树1、右子树1都是空树,使用右-左双旋之后,树结构如下图,该树得以重新平衡:
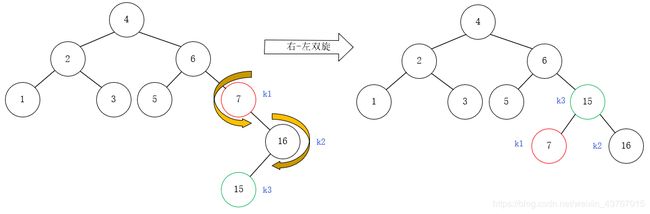
接着插入14,情况与刚才类似,节点6的BF是-2,此时符合RL的情况(在节点6的右孩子节点15的左子树7中插入元素),如下图左,此时继续右-左双旋后,整棵树又回到了平衡状态,如下图右:
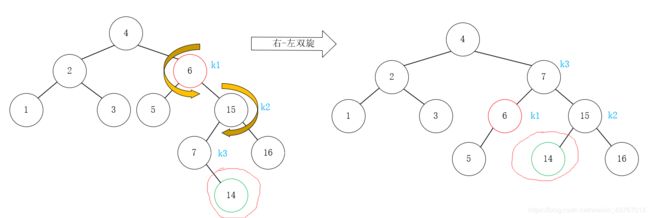
继续插入13,此时根节点4的BF变成了-2,符合情况4,此时使用一次单左旋即可解决问题:
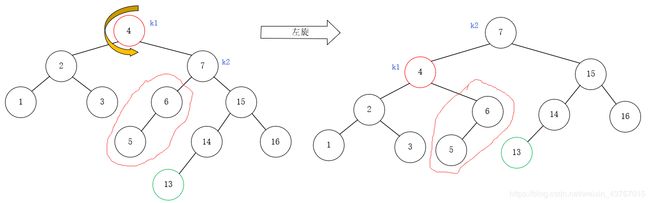
继续插入12之后,向上回溯到节点14时,发现节点14的BF为2,此时符合情况1,需要右旋恢复平衡:
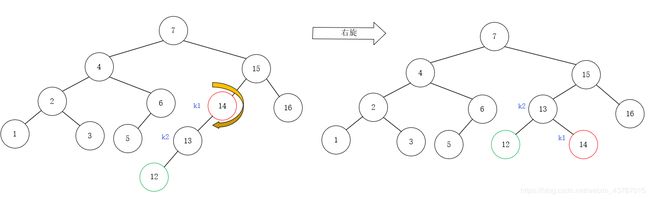
继续插入11之后,向上回溯到节点15时,发现节点15的BF为2,此时符合情况1,需要右旋恢复平衡:
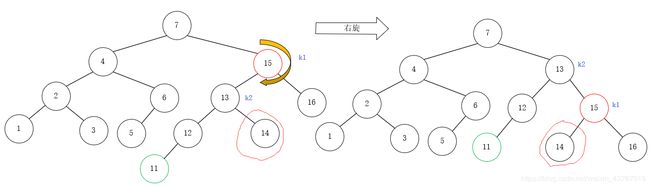
继续插入10之后,向上回溯到节点12时,发现节点12的BF为2,此时符合情况1,需要右旋恢复平衡:
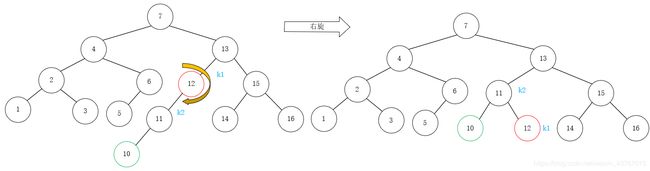
插入8之后,向上回溯到根节点也没有发现最小不平衡树,因此不需要旋转。最后插入9之后,我们发现出现了情况2,此时我们有情况1和情况对称的经验,自然也知道需要右-左双旋的的对称操作,左-右双旋来重新平衡。
先来看左-右双旋模型:
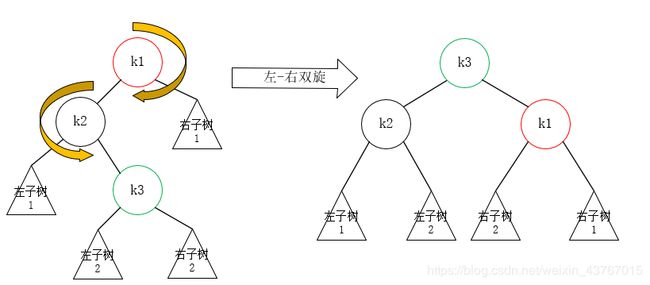
它和右-左双旋模型就是对称操作,将k3当作新的根节点,并且先使得k2左旋成为k3的左子树,然后k1右旋成为k3的右子树,并且左子树2成为k2的右子树,右子树2成为k1的左子树,这是完全成立的,这就是情况2的通解。
左-右双旋之后,重新形成了平衡二叉树:
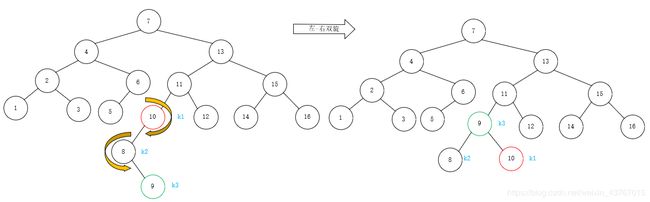
实际上,左-右双旋,分开旋转的过程模型如下:
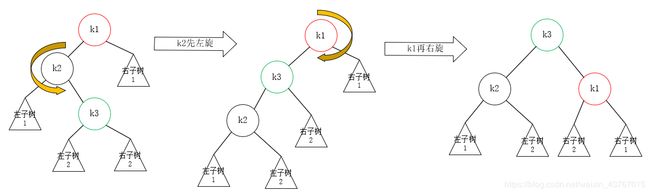
节点添加完毕,最终形成了一颗平衡二叉树:
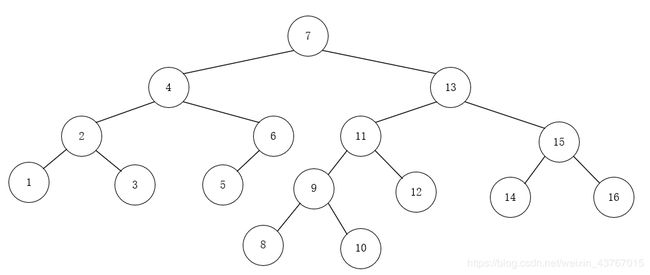
2.3 总结
插入节点的不平衡的情况只有四种:
在节点X的左孩子节点的左子树中插入元素,简称LL
在节点X的左孩子节点的右子树中插入元素,简称LR
在节点X的右孩子节点的左子树中插入元素,简称RL
在节点X的右孩子节点的右子树中插入元素,简称RR
其中1采用单右旋、4采用单左旋即可解决问题。2和3比较复杂,2需要采用左-右双旋、3需要采用右-左双旋。
1和4、2和3是对称的情况,现在综合起来看,所谓的旋转似乎也不那么复杂,并且我们已经求出了这几种问题的通解,该通解对于节点的删除是同样适用的,不必再考虑各种特殊情况,非常方便,下面来看看具体的代码实现!
3 平衡二叉树的构建
3.1 类架构
首先节点对象还是需要一个数据域和两个引用域,相比于二叉排序树,还要多一个节点高度的字段,这样方便计算平衡因子,并且提供返回节点高度的方法。
另外还需要一个比较器的引用,因为需要对元素进行排序,自然需要比较元素的大小,如果外部传递了比较器,那么就使用用户指定的比较器进行比较,否则,数据类型E必须是Comparable接口的子类,否则因为不能比较而报错。
另外,还需要提供中序遍历的方法,该遍历方法对于二叉排序树的结果将会顺序展示。
public class AvlTree {
/**
* 外部保存根节点的引用
*/
private BinaryTreeNode root;
/**
* 自定义比较器
*/
private Comparator super E> cmp;
/**
* 树节点的数量
*/
private int size;
/**
* 内部节点对象
*
* @param 数据类型
*/
public static class BinaryTreeNode {
//数据域
E data;
//左子节点
BinaryTreeNode left;
//右子节点
BinaryTreeNode right;
//节点高度 从0开始,从下往上;null节点高度返回-1
int height;
public BinaryTreeNode(E data) {
this.data = data;
}
@Override
public String toString() {
return data.toString();
}
}
/**
* 指定比较器
*
* @param cmp 比较器
*/
public AvlTree(Comparator super E> cmp) {
this.cmp = cmp;
}
/**
* 空构造器
*/
public AvlTree() {
}
/**
* 是否是空树
*
* @return true 是 ;false 否
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 返回节点数
*
* @return 节点数
*/
public int size() {
return size;
}
/**
* 对元素进行比较大小的方法,如果传递了自定义比较器,则使用自定义比较器,否则则需要数据类型实现Comparable接口
*
* @param e1 被比较的第一个对象
* @param e2 被比较的第二个对象
* @return 0 相等 ;小于0 e1 < e2 ;大于0 e1 > e2
*/
private int compare(E e1, E e2) {
if (cmp != null) {
return cmp.compare(e1, e2);
} else {
return ((Comparable) e1).compareTo(e2);
}
}
/**
* 保存遍历出来的节点数据
*/
List> str = new ArrayList<>();
/**
* 中序遍历,提供给外部使用的api
*
* @return 遍历的数据
*/
public String toInorderTraversalString() {
//如果是空树,直接返回空
if (isEmpty()) {
return null;
}
//从根节点开始递归
inorderTraversal(root);
//获取遍历结果
String s = str.toString();
str.clear();
return s;
}
/**
* 中序遍历 内部使用的递归遍历方法,借用了栈的结构
*
* @param root 节点,从根节点开始
*/
private void inorderTraversal(BinaryTreeNode root) {
BinaryTreeNode left = getLeft(root);
if (left != null) {
//如果左子节点不为null,则继续递归遍历该左子节点
inorderTraversal(left);
}
//添加数据节点
str.add(root);
//获取节点的右子节点
BinaryTreeNode right = getRight(root);
if (right != null) {
//如果右子节点不为null,则继续递归遍历该右子节点
inorderTraversal(right);
}
}
/**
* 获取左子节点
*
* @param parent 父节点引用
* @return 左子节点或者null--表示没有左子节点
*/
public BinaryTreeNode getLeft(BinaryTreeNode parent) {
return parent == null ? null : parent.left;
}
/**
* 获取右子节点
*
* @param parent 父节点引用
* @return 右子节点或者null--表示没有右子节点
*/
public BinaryTreeNode getRight(BinaryTreeNode parent) {
return parent == null ? null : parent.right;
}
/**
* 获取根节点
*
* @return 根节点 ;或者null--表示空树
*/
public BinaryTreeNode getRoot() {
return root;
}
/**
* 获取height
*
* @param node 节点
* @return 高度或者-1 表示节点为null
*/
private int getHeight(BinaryTreeNode node) {
return node == null ? -1 : node.height;
}
}
3.2 查找的方法
平衡二叉树就是一颗二叉排序树,其查找方法可以复用二叉排序树的查找方法,很简单:
若根节点的关键字值等于查找的关键字,成功,返回true;
否则,若小于根节点的关键字值,递归查左子树;
若大于根节点的关键字值,递归查右子树;
最终查找到叶子节点还是没有数据,那么查找失败,则返回false
/**
* 查找,开放给外部使用的api
* @param e 要查找的元素
* @return false 不存在 true 存在
*/
public boolean contains(E e) {
return contains(e, root);
}
/**
* 查找,内部调用的方法,从根节点开始查找
*
* @param e 要查找的元素
* @param root 节点
* @return false 不存在 true 存在
*/
private boolean contains(E e, BinaryTreeNode root) {
/*null校验*/
if (root == null) {
return false;
}
/*调用比较的方法*/
int i = compare(e, root.data);
/*如果大于0,则说明e>root.date 继续查询右子树*/
if (i > 0) {
return contains(e, root.right);
/*如果小于0,则说明e} else if (i < 0) {
return contains(e, root.left);
} else {
/*如果等于0,则说明e=root.date 即查询成功*/
return true;
}
}
3.3 检查是否平衡的方法
很简单,只需要递归的查看所有节点,判断是否存在的节点的左右子节点高度差绝对值是否大于1的情况就能判断了,如果存在,那么返回false表示不是平衡二叉树,不存在就返回true表示是平衡二叉树。
/**
* 保存是否平衡的标志
*/
private boolean balance = true;
/**
* 检查是否是平衡二叉树的方法,当然也可以debug看,如果你不嫌麻烦……
*
* @return true 是 ;false 否
*/
public boolean checkBalance() {
checkBalance(root);
boolean balanceNow=balance;
balance=true;
return balanceNow;
}
/**
* 递归检查是否平衡,实际上这里采用了后序遍历,即左子节点-右子节点-根节点的方法递归遍历检查
*
* @param root 根节点
* @return 节点的高度
*/
private int checkBalance(BinaryTreeNode root) {
if (root == null) {
return -1;
}
//返回左子树的高度
int hl = checkBalance(root.left);
//返回右子树的高度
int hr = checkBalance(root.right);
//如果root的左右子树高度差绝对值大于1,或者checkBalance和getHeight方法获取的左/右子树高度不一致,那么算作不平衡
if (Math.abs(getHeight(root.left) - getHeight(root.right)) > 1 ||
getHeight(root.left) != hl || getHeight(root.right) != hr) {
balance = false;
}
return getHeight(root);
}
3.4 插入的方法
平衡二叉树和二叉排序树的最大区别就是在插入和删除的时候了。我们已经讨论过插入之后的4种出现平衡问题的特殊情况,这里不再赘述,下面看代码具体如何实现:
/**
* 插入,开放给外部使用的api
*
* @param e 要插入的元素
*/
public void insert(E e) {
//返回root,但此时新的节点可能已经被插入进去了
root = insert(e, root);
}
/**
* 插入,开放给外部使用的api
*
* @param es 要插入的元素的数组,注意,数组元素的顺序存储的位置将会影响二叉排序树的生成
*/
public void insert(E[] es) {
//返回root,但此时新的节点可能已经被插入进去了
for (E e : es) {
root = insert(e, root);
}
}
/**
* 插入,内部调用的方法,先从根节点开始递归查找要插入的位置,然后插入
* 大部分代码都和排序二叉树的相似,区别就是在插入之后,会调用尝试重平衡的方法rebalance
*
* @param e 要插入的数据
* @param root 节点
* @return 原节点重平衡之后的节点或者新插入的节点
*/
private BinaryTreeNode insert(E e, BinaryTreeNode root) {
/*没有查找到,那么直接构建新的节点返回,将会在上一层方法中被赋值给其父节点的某个引用,这个插入的位置肯定是该遍历路径上的最后一点
* 即插入的元素节点肯定是属于叶子节点*/
if (root == null) {
size++;
return new BinaryTreeNode<>(e);
}
/*调用比较的方法*/
int i = compare(e, root.data);
/*如果大于0,则说明e>root.date 继续查询右子树*/
if (i > 0) {
//重新赋值
root.right = insert(e, root.right);
/*如果小于0,则说明e} else if (i < 0) {
//重新赋值
root.left = insert(e, root.left);
} else {
/*如果等于0,则说明e=root.date 即存在节点 什么都不做*/
}
/*insert递归插入之后,在返回时,会调用重新平衡并且设置高度的方法 尝试重平衡root根节点 而不是像排序二叉树一样简单的返回root
*从新插入节点的父节点一直向上回溯直到根节点,尝试寻找最小不平衡树,找到之后会进行平衡,返回返回平衡之后的树,.*/
return rebalance(root);
}
/**
* 重平衡的方法
* 1)在节点X的左孩子节点的左子树中插入元素,简称LL 右旋
* 2)在节点X的左孩子节点的右子树中插入元素,简称LR 左-右双旋
* 3)在节点X的右孩子节点的左子树中插入元素,简称RL 左旋
* 4)在节点X的右孩子节点的右子树中插入元素,简称RR 右-左双旋
*
* @param root 树的根节点,无论是否是最小不平衡树,都是走这个方法
* @return 平衡之后的树的根节点
*/
private BinaryTreeNode rebalance(BinaryTreeNode root) {
/*1、如果节点为null,直接返回null*/
if (root == null) {
return null;
}
/*2、开始旋转*/
/*2.1、如果左子树的高度减去右子树的高度值大于1,说明左子树的高度大于右子树的高度至少2层,可能是情况1、2 继续判断*/
if (getHeight(root.left) - getHeight(root.right) > 1) {
/*如果左子节点的左子节点高度大于左子节点的右子节点高度,那说明是情况1,否则是情况2*/
if (getHeight(root.left.left) >= getHeight(root.left.right)) {
/*2.1.1、右旋*/
root = rotateRight(root);
} else {
/*2.1.2、左-右双旋*/
root = rotateLeftAndRight(root);
}
/*2.2、如果右子树的高度减去左子树的高度值大于1,说明右子树的高度大于左子树的高度至少2层,可能是情况3、4 继续判断*/
} else if (getHeight(root.right) - getHeight(root.left) > 1) {
/*如果右子节点的右子节点高度大于右子节点的左子节点高度,那说明是情况4,否则是情况3*/
if (getHeight(root.right.right) >= getHeight(root.right.left)) {
/*2.2.1、左旋*/
root = rotateLeft(root);
} else {
/*2.2.2、右-左双旋*/
root = rotateRightAndLeft(root);
}
}
/*3、到这一步,说明旋转完毕,或者不需要旋转,但是都需要重新计算高度,高度为左/右子树高度最大值+1*/
root.height = Math.max(getHeight(root.left), getHeight(root.right)) + 1;
return root;
}
/**
* 右旋
* 通解:右旋之后,k2成为根节点,k1成为k2的右子节点,k2的右子树2成为k1的左子树
*
* @param k1 需要旋转的最小不平衡树根节点
* @return k2 旋转后的最小不平衡树根节点, 已经转换为平衡二叉树
*/
private BinaryTreeNode rotateRight(BinaryTreeNode k1) {
//获取k2,k2是k1的左子节点
BinaryTreeNode k2 = k1.left;
//k2的右子树成为k1的左子树
k1.left = k2.right;
//k1成为k2的右子节点
k2.right = k1;
//k1的高度等于k1的左或者右子树的高度的最大值+1;
k1.height = Math.max(getHeight(k1.left), getHeight(k1.right)) + 1;
//k2的高度等于k2的左子节点和k1的高度(此时k1就是k2的右子节点)的最大值+1
k2.height = Math.max(getHeight(k2.left), k1.height) + 1;
//返回k2,k2成为根节点
return k2;
}
/**
* 左旋 很简单,实际上就是右旋的镜像
* 通解:左旋之后,k2成为根节点,k1成为k2的左子节点,k2的左子树2成为k1的右子树
*
* @param k1 需要旋转的最小不平衡树根节点
* @return k2 旋转后的最小不平衡树根节点, 已经转换为平衡二叉树
*/
private BinaryTreeNode rotateLeft(BinaryTreeNode k1) {
//获取k2,k2是k1的右子节点
BinaryTreeNode k2 = k1.right;
//k2的左子树成为k1的右子树
k1.right = k2.left;
//k1成为k2的左子节点
k2.left = k1;
//k1的高度等于k1的左或者右子树的高度的最大值+1;
k1.height = Math.max(getHeight(k1.left), getHeight(k1.right)) + 1;
//k2的高度等于k2的右子节点和k1的高度(此时k1就是k2的左子节点)的最大值+1
k2.height = Math.max(getHeight(k2.right), k1.height) + 1;
//返回k2,k2成为根节点
return k2;
}
/**
* 右-左双旋
* 通解:将k3当作新的根节点,并且先使得k2右旋成为k3的右子树,然后k1左旋成为k3的左子树,并且左子树2成为k1的右子树,右子树2成为k2的左子树
*
* @param k1 需要旋转的最小不平衡树根节点
* @return 旋转后的最小不平衡树根节点, 已经转换为平衡二叉树
*/
private BinaryTreeNode rotateRightAndLeft(BinaryTreeNode k1) {
/*1、先对k1的右子节点k2进行右旋,返回右旋之后的根节点k3,然后使得成为k3成为的k1的左子树*/
k1.right = rotateRight(k1.right);
/*2、然后对k1进行左旋,成为k3的左子树,返回的根节点就是k3,即返回旋转之后的根节点*/
return rotateLeft(k1);
}
/**
* 左-右双旋 很简单,实际上就是右-左双旋的镜像
* 通解: 将k3当作新的根节点,并且先使得k2左旋成为k3的左子树,然后k1右旋成为k3的右子树,并且左子树2成为k2的右子树,右子树2成为k1的左子树
*
* @param k1 需要旋转的最小不平衡树根节点
* @return 旋转后的最小不平衡树根节点, 已经转换为平衡二叉树
*/
private BinaryTreeNode rotateLeftAndRight(BinaryTreeNode k1) {
/*1、先对k1的左子节点k2进行左旋,返回左旋之后的根节点k3,然后使得成为k3成为的k1的左子树*/
k1.left = rotateLeft(k1.left);
/*2、然后对k1进行右旋,成为k3的右子树,返回的根节点就是k3,即返回旋转之后的根节点*/
return rotateRight(k1);
}
3.4.1 测试
AvlTree avlTree = new AvlTree<>();
Integer[] es = new Integer[]{3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9};
//批量插入
avlTree.insert(es);
//中序遍历输出
System.out.println(avlTree.toInorderTraversalString());
//检查是否平衡
System.out.println(avlTree.checkBalance());
//数量
System.out.println(avlTree.size());
在insert之后打上断点,Debug,可以看到avlTree的数据结构和在实现原理中最终的结构是一致的。
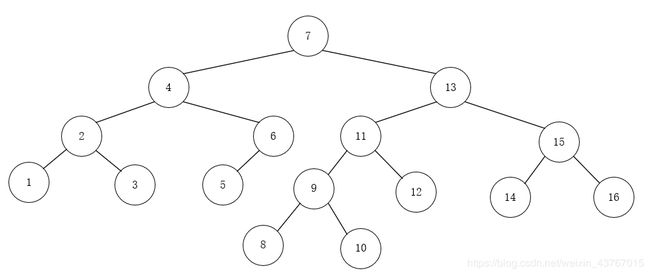
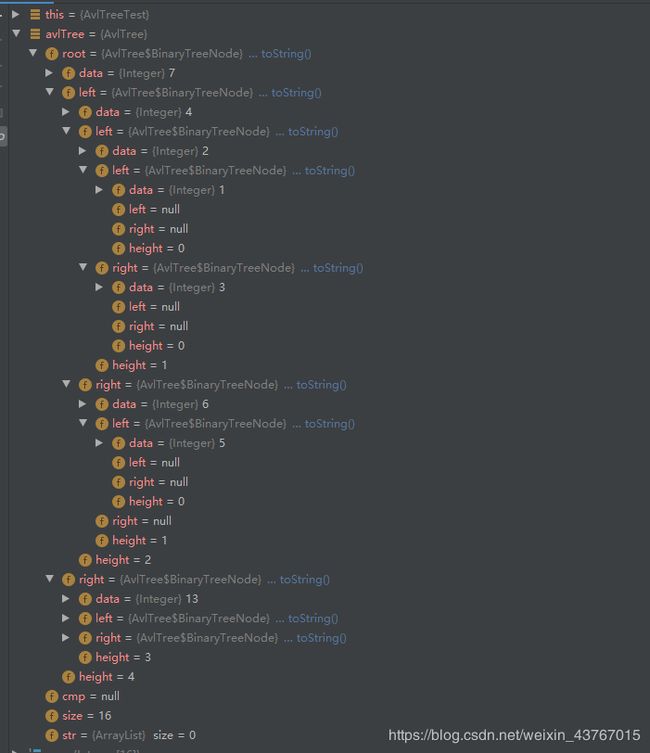
3.5 查找最大值和最小值
很简单,最左边的节点一定是最小的,最右边的节点一定是最大的。因此查找最小的节点只需要向左递归查找,查找最大的节点只需要向右递归查找。
/**
* 查找最小的节点
*
* @param root 根节点
* @return 最小的节点
*/
private BinaryTreeNode findMin(BinaryTreeNode root) {
if (root == null) {
return null;
/*如果该节点没有左右子节点,那么该节点就是最小的节点,返回*/
} else if (root.left == null) {
return root;
}
/*如果该节点存在左子节点,那么继续向左递归查找*/
return findMin(root.left);
}
/**
* 查找最大的节点
*
* @param root 根节点
* @return 最大的节点
*/
private BinaryTreeNode findMax(BinaryTreeNode root) {
if (root == null) {
return null;
/*如果该节点没有右子节点,那么该节点就是最大的节点,返回*/
} else if (root.right == null) {
return root;
}
/*如果该节点存在右子节点,那么继续向右递归查找*/
return findMax(root.right);
}
3.6 删除的方法
平衡二叉树节点的删除同样可能导致产生不平衡的状态,因此同样在二叉排序树的删除代码的基础上,删除元素之后需要在删除节点之上进行回溯直到根节点,尝试找出最小不平衡树来进行重平衡。其平衡的方法是和插入的时候是一样的。
/**
* 删除,开放给外部使用的api
*
* @param e 要删除的元素
*/
public void delete(E e) {
//返回root,但此时可能有一个节点已经被删除了
root = delete(e, root);
}
/**
* 删除,内部调用的方法,删除分为三种情况: 1、该节点没有子节点 2、该字节仅有一个子节点 3、该节点具有两个子节点
*
* @param e 要删除的数据
* @param root (子)树根节点
* @return 该根节点重平衡之后的节点
*/
private BinaryTreeNode delete(E e, BinaryTreeNode root) {
/*没有查找到,那么什么都不做*/
if (root == null) {
return null;
}
/*调用比较的方法*/
int i = compare(e, root.data);
/*如果大于0,则说明e>root.date 继续查询右子树*/
if (i > 0) {
//重新赋值
root.right = delete(e, root.right);
/*如果小于0,则说明e} else if (i < 0) {
//重新赋值
root.left = delete(e, root.left);
} else {
/*如果等于0,则说明e=root.date 即查询成功 开始执行删除*/
/*如果两个子节点都不为null*/
if (root.left != null && root.right != null) {
/*递归查找最小的节点,然后递归删除*/
root.data = findMin(root.right).data;
root.right = delete(root.data, root.right);
} else {
/*如果一个子节点不为null,则返回该子节点;或者两个子节点都为null,则返回null
* 此时该root节点已经被"绕过了"*/
root = (root.left != null) ? root.left : root.right;
--size;
}
}
/*和二叉排序树直接返回节点不同的是,删除操作完成之后将会调用该方法,从被删除节点回溯至根节点,对节点进行重平衡,然后才返回平衡后的节点*/
return rebalance(root);
}
3.6.1 测试
针对上面插入的平衡二叉树进行删除:
System.out.println("======>首先删除5 此时没有影响,不需要重平衡");
avlTree.delete(5);
//检查是否平衡
System.out.println(avlTree.checkBalance());
//中序遍历输出
System.out.println(avlTree.toInorderTraversalString());
System.out.println("======>再次删除6 此时节点4的BF为2 需要右旋重平衡");
avlTree.delete(6);
//检查是否平衡
System.out.println(avlTree.checkBalance());
//中序遍历输出
System.out.println(avlTree.toInorderTraversalString());
System.out.println("======>再次删除11 由于该节点拥有左右子树,实际上删除的是该节点的右子树的最小节点12,然后将12的值赋值给11的节点,并导致节点12的原父节点11不平衡,需要重平衡");
avlTree.delete(11);
//检查是否平衡
System.out.println(avlTree.checkBalance());
//中序遍历输出
System.out.println(avlTree.toInorderTraversalString());
System.out.println("======>再次删除7 由于该节点拥有左右子树,实际上删除的是该节点的右子树的最小节点8,然后将8的值赋值给7的节点,并导致节点8的原父节点9不平衡,需要重平衡");
avlTree.delete(7);
//检查是否平衡
System.out.println(avlTree.checkBalance());
//中序遍历输出
System.out.println(avlTree.toInorderTraversalString());
System.out.println("======>再次删除9、12 此时不需要重平衡");
avlTree.delete(9);
avlTree.delete(12);
//检查是否平衡
System.out.println(avlTree.checkBalance());
//中序遍历输出
System.out.println(avlTree.toInorderTraversalString());
System.out.println("======>最后删除8 由于该节点拥有左右子树,实际上删除的是该节点的右子树的最小节点10节点,然后将10的值赋值给8的节点,并导致节点10的原父节点13不平衡,需要重平衡");
avlTree.delete(8);
//检查是否平衡
System.out.println(avlTree.checkBalance());
//中序遍历输出
System.out.println(avlTree.size());
System.out.println(avlTree.toInorderTraversalString());
在进行上面的一系列删除之后,树结构会变成如下形状:
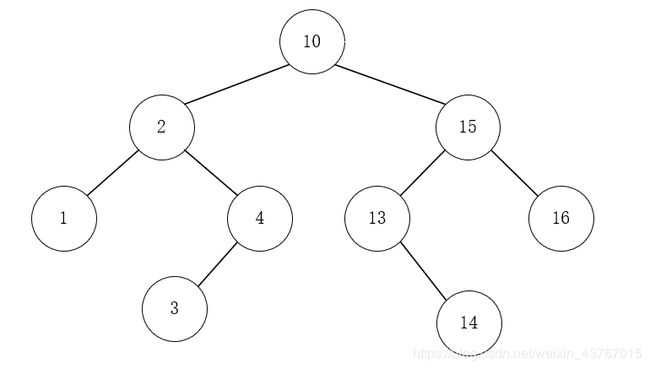
4 平衡二叉树的总结
平衡二叉树是基于二叉排序树的,但是由于其必须保持平衡的特性,因此其编码难度比二叉排序树的编码难度更高,不过如果我们搞懂了其旋转的原理,那么实现起来还是比较简单的。
如果我们需要查找的集合本身没有顺序,在频繁查找的同时也需要经常的插入和删除操作,显然我们需要构建一棵二叉排序树,但是不平衡的二叉排序树,极端情况下可能退化为链表,查找效率是非常低的,因此我们需要在构建时,就让这棵二叉排序树是动态的转换为平衡二叉树,此时我们的查找时间复杂度就为O(logn),而插入和删除也为O(logn)。这显然是比较理想的一种动态查找表算法。
本文介绍了平衡二叉树的原理以及Java代码的完全实现,要想搞懂平衡二叉树需要先搞懂二叉排序树:二叉排序树的详解以及Java代码的完全实现。而搞懂平衡二叉树又是搞懂红黑树的基础,后续文章我们将会介绍红黑树的概念以及Java代码的完全实现!
参考
《算法》
《数据结构与算法分析》
《大话数据结构》
如果有什么不懂或者需要交流,可以留言。另外希望点赞、收藏、关注,我将不间断更新各种Java学习博客!


