LeetCode——第 404 场周赛

周赛

三角形的最大高度

给你两个整数 red 和 blue，分别表示红色球和蓝色球的数量。你需要使用这些球来组成一个三角形，满足第 1 行有 1 个球，第 2 行有 2 个球，第 3 行有 3 个球，依此类推。

每一行的球必须是 相同 颜色，且相邻行的颜色必须 不同。

返回可以实现的三角形的 最大 高度。

示例 1：

输入： red = 2, blue = 4

输出： 3

解释：

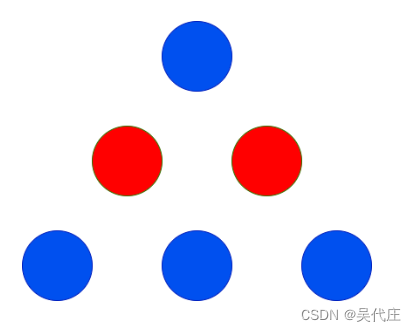
上图显示了唯一可能的排列方式。

解题思路

三角形的首行可能放置红色球或蓝色球，当首行颜色确定之后，三角形的每一行的颜色都可以确定。

对于两种情况，分别枚举每一行，计算是否可以使用指定颜色的球完整放置该行，可以使用指定颜色的球完整放置的最大行数即为三角形的最大高度。

class Solution {
    public int maxHeightOfTriangle(int red, int blue) {
        return Math.max(getMaxHeight(new int[]{red, blue}), getMaxHeight(new int[]{blue, red}));
    }

    public int getMaxHeight(int[] counts) {
        int height = 0;
        int position = 0;
        while (height + 1 <= counts[position]) {
            height++;
            counts[position] -= height;
            position ^= 1;
        }
        return height;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

找出有效子序列的最大长度 I

给你一个整数数组 nums。

nums 的子序列 sub 的长度为 x ，如果其满足以下条件，则称其为 有效子序列：

(sub[0] + sub[1]) % 2 == (sub[1] + sub[2]) % 2 == … == (sub[x - 2] + sub[x - 1]) % 2
返回 nums 的 最长的有效子序列 的长度。

一个 子序列 指的是从原数组中删除一些元素（也可以不删除任何元素），剩余元素保持原来顺序组成的新数组。

示例 1：

输入： nums = [1,2,3,4]

输出： 4

解释：

最长的有效子序列是 [1, 2, 3, 4]。

解题思路

对于子序列 sub，每对连续元素的和应具有相同的奇偶性

class Solution {
    public int maximumLength(int[] nums) {
        int c = nums[0] % 2, odd = 0, even = 0, both = 0;//both 记录01，10交替出现的长度
        for (int num: nums){
            int cur = num % 2;
            if (cur==0){
                even++;
            }else{
                odd++;
            }
            if (cur == c){
                both++;
                c^=1;
            }
        }
        return Math.max(both, Math.max(even, odd));
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

找出有效子序列的最大长度 II

给你一个整数数组 nums 和一个 正 整数 k 。
nums 的一个
子序列
sub 的长度为 x ，如果其满足以下条件，则称其为 有效子序列 ：

(sub[0] + sub[1]) % k == (sub[1] + sub[2]) % k == … == (sub[x - 2] + sub[x - 1]) % k
返回 nums 的 最长有效子序列 的长度。

示例 1：

输入：nums = [1,2,3,4,5], k = 2

输出：5

解释：

最长有效子序列是 [1, 2, 3, 4, 5] 。

解题思路

通过一个两层循环，预处理出能与nums[i]产生余数rem的右侧第一个nums[j]，用哈希表记录下标j。然后检查n个起点所有可能的余数对应的最长的子序列长度，由于前述的预处理，我们可以快速地查出来下一个下标，查不出来说明子序列结束。

class Solution {
    public int maximumLength(int[] nums, int k) {
        int n = nums.length;
        Map<Integer, Integer>[] next = new Map[nums.length];
        Arrays.setAll(next, key -> new HashMap<>());
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int rem = (nums[i] + nums[j]) % k;
                next[i].putIfAbsent(rem, j);
            }
        }
        int[][] memo = new int[n][k + 1];
        for (var it : memo) {
            Arrays.fill(it, -1);
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            for (int r : next[i].keySet()) {
                ans = Math.max(ans, dfs(next, i, r, memo));
            }
        }
        return ans + 1;
    }

    private int dfs(Map<Integer, Integer>[] next, int i, int rem, int[][] memo) {
        if (memo[i][rem] != -1) {
            return memo[i][rem];
        }
        if (!next[i].containsKey(rem)) {
            return 0;
        }
        return memo[i][rem] = 1 + dfs(next, next[i].get(rem), rem, memo);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

合并两棵树后的最小直径

给你两棵 无向 树，分别有 n 和 m 个节点，节点编号分别为 0 到 n - 1 和 0 到 m - 1 。给你两个二维整数数组 edges1 和 edges2 ，长度分别为 n - 1 和 m - 1 ，其中 edges1[i] = [ai, bi] 表示在第一棵树中节点 ai 和 bi 之间有一条边，edges2[i] = [ui, vi] 表示在第二棵树中节点 ui 和 vi 之间有一条边。

你必须在第一棵树和第二棵树中分别选一个节点，并用一条边连接它们。

请你返回添加边后得到的树中，最小直径 为多少。

一棵树的 直径 指的是树中任意两个节点之间的最长路径长度。

示例 1：

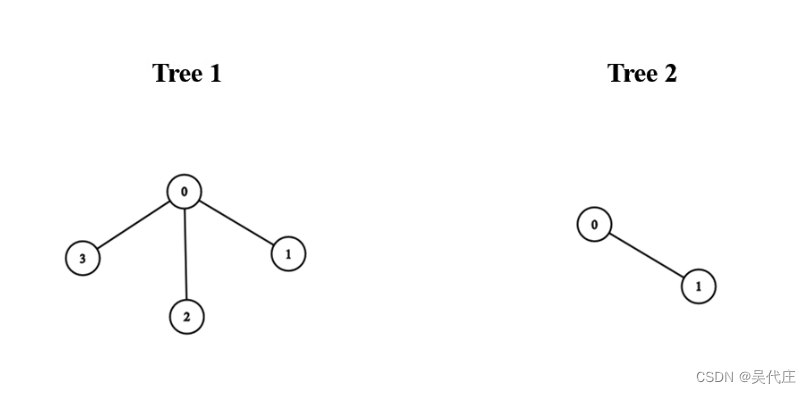
输入：edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]

输出：3

解释：

将第一棵树中的节点 0 与第二棵树中的任意节点连接，得到一棵直径为 3 得树。

class Solution {
    int diameter;

    public int minimumDiameterAfterMerge(int[][] edges1, int[][] edges2) {
        int diameter1 = treeDiameter(edges1), diameter2 = treeDiameter(edges2);
        int semiDiameter1 = (diameter1 + 1) / 2, semiDiameter2 = (diameter2 + 1) / 2;
        return Math.max(Math.max(diameter1, diameter2), semiDiameter1 + semiDiameter2 + 1);
    }

    public int treeDiameter(int[][] edges) {
        diameter = 0;
        int n = edges.length + 1;
        List<Integer>[] adjacentArr = new List[n];
        List<Integer>[] childrenArr = new List[n];
        for (int i = 0; i < n; i++) {
            adjacentArr[i] = new ArrayList<Integer>();
            childrenArr[i] = new ArrayList<Integer>();
        }
        for (int[] edge : edges) {
            adjacentArr[edge[0]].add(edge[1]);
            adjacentArr[edge[1]].add(edge[0]);
        }
        getTree(adjacentArr, childrenArr, -1, 0);
        getDepth(childrenArr, 0);
        return diameter;
    }

    public void getTree(List<Integer>[] adjacentArr, List<Integer>[] childrenArr, int parent, int curr) {
        if (parent >= 0) {
            childrenArr[parent].add(curr);
        }
        List<Integer> adjacent = adjacentArr[curr];
        for (int next : adjacent) {
            if (next != parent) {
                getTree(adjacentArr, childrenArr, curr, next);
            }
        }
    }

    public int getDepth(List<Integer>[] childrenArr, int node) {
        List<Integer> children = childrenArr[node];
        int first = 0, second = 0;
        for (int child : children) {
            int depth = getDepth(childrenArr, child);
            if (depth > first) {
                second = first;
                first = depth;
            } else if (depth > second) {
                second = depth;
            }
            diameter = Math.max(diameter, first + second);
        }
        return first + 1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

解题思路

这道题给定两个无向树，要求在两个树中各选择一个结点，使用一条边连接这两个结点得到合并后的树，计算合并后的树的最小直径。

来源

LeetCode