排序算法——快速排序（队列和栈实现非递归）

一、背景 

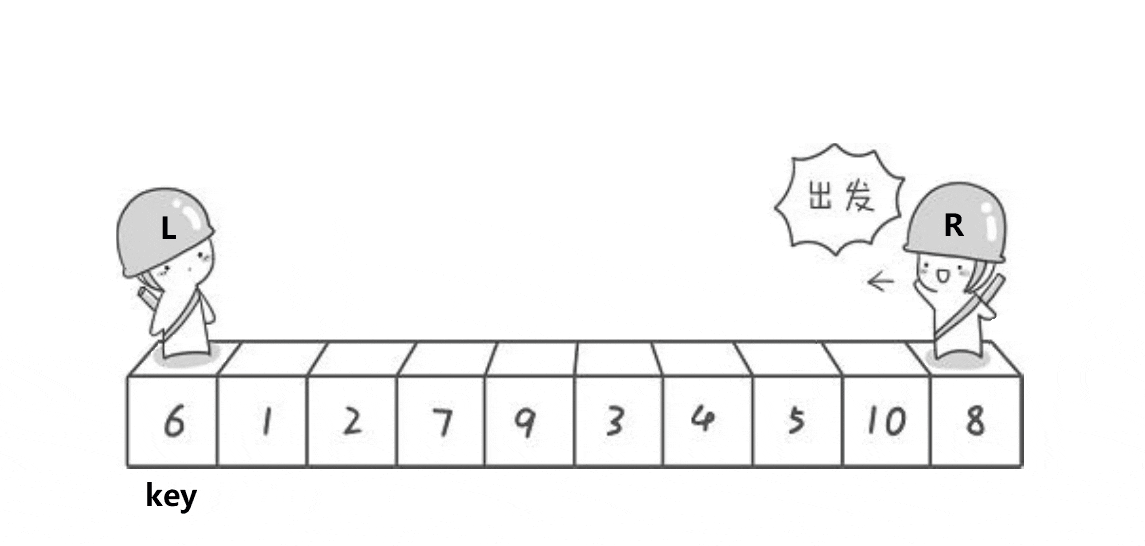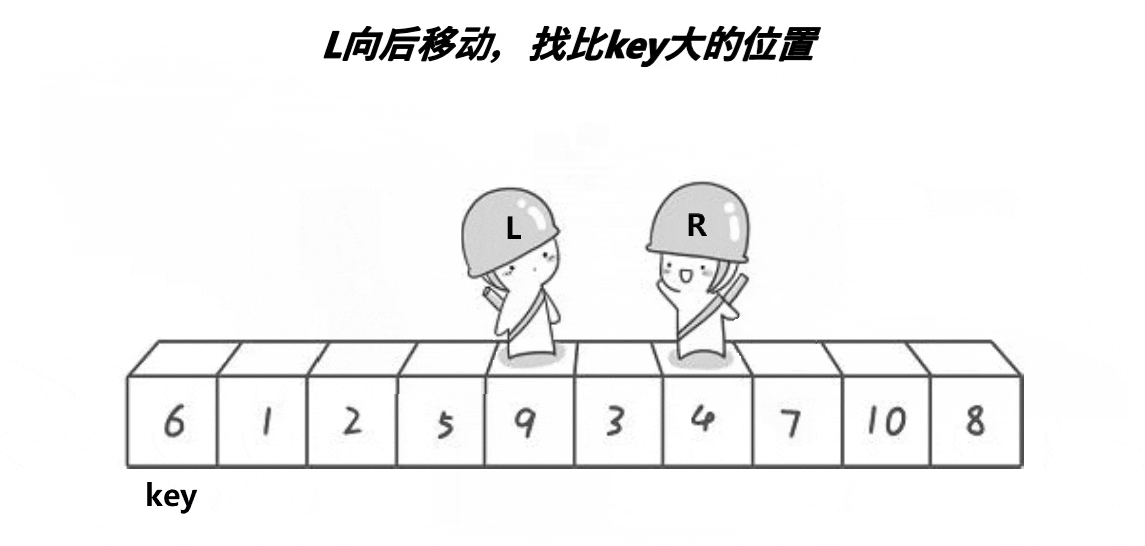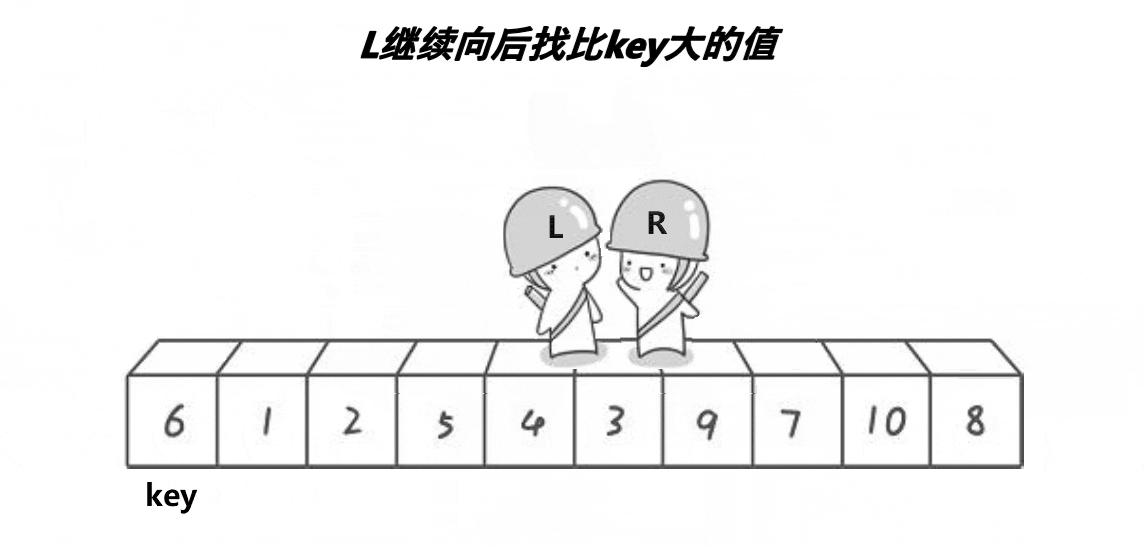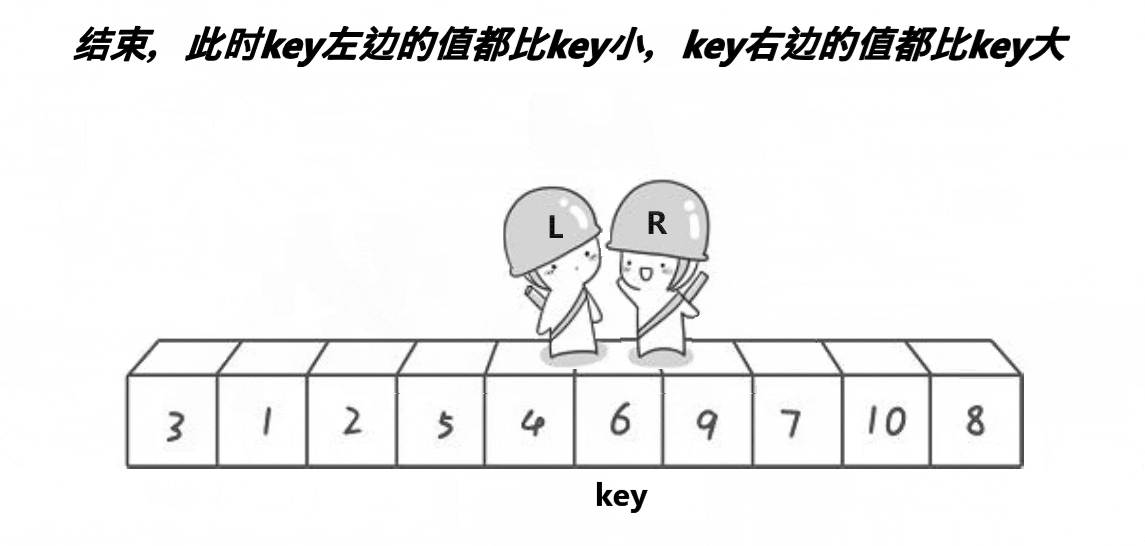
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。本博客以hoare版本为例

二、实现

1、hoare版本

 

老规矩我们先写单趟：

以最左边元素为基准：右边先走，找到左边大于key的数，右边小于key的数：

int key = left;
int begin = left;
int end = right - 1;
while (a[end] >= a[key])//在右边找到第一个比key小的值
{
	end--;
}
while(a[begin] <= a[key])//在左边找到第一个比key大的值
{
	begin++;
}
swap(&a[begin], &a[end]);

相遇时说明第一趟排好，所以我们可以写出如下代码：

int PartSort1(int* a, int left, int right)
{
	int key = left;
	int begin = left;
	int end = right - 1;
	while (begin < end);
	{
		
		while (a[end] >= a[key])//在右边找到第一个比key小的值
		{
			end--;
		}
		while (a[begin] <= a[key])//在左边找到第一个比key大的值
		{
			begin++;
		}
		swap(&a[begin], &a[end]);
	}
	
}

剩下的排序类似树的左右子树遍历用递归实现：
递归结束条件为剩余长度<=1（也可以写成right<=left），注意在经行找值的时候，还要保持左小于右。

void QuickSort(int* a, int left, int right)
{
	if (right-left<=1)
	{
		return;
	}
	int key = left;
	int begin = left;
	int end = right;
	while (begin < end)
	{
		while (begin < end && a[end] >= a[key])//在右边找到第一个比key小的值
		{
			--end;
		}
		while (begin < end && a[begin] <= a[key])//在左边找到第一个比key大的值
		{
			++begin;
		}
		swap(&a[begin], &a[end]);
	}
	swap(&a[begin], &a[key]);
	key = begin;
	QuickSort(a, left, key-1);
	QuickSort(a, key+1, right);
}

2、挖矿法

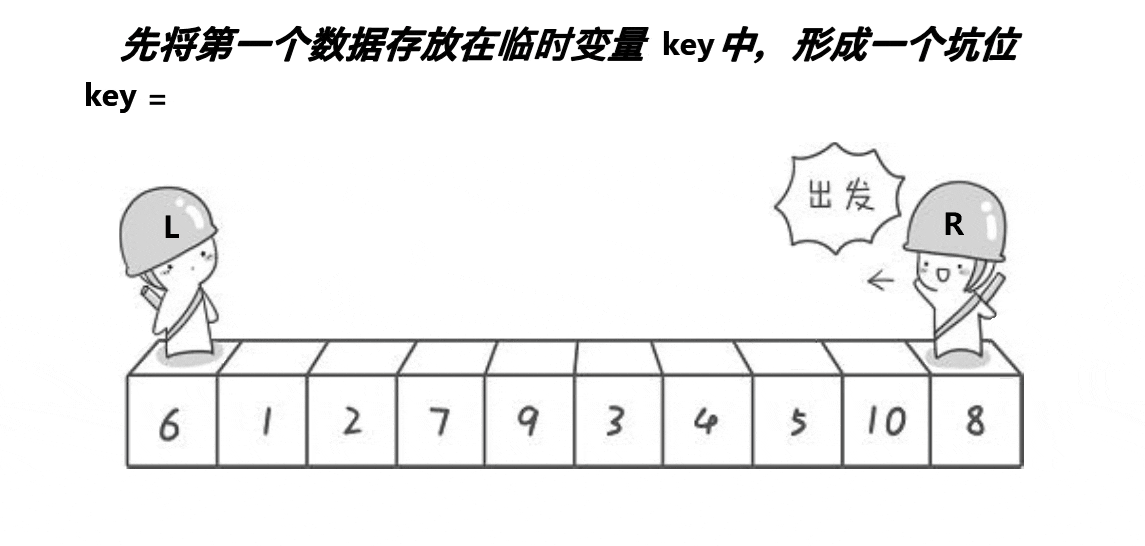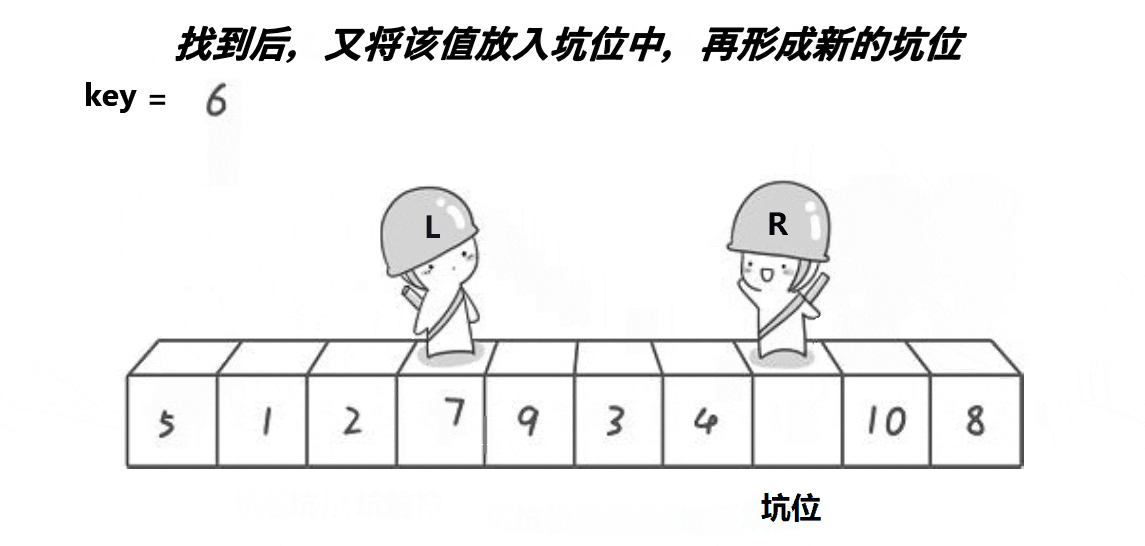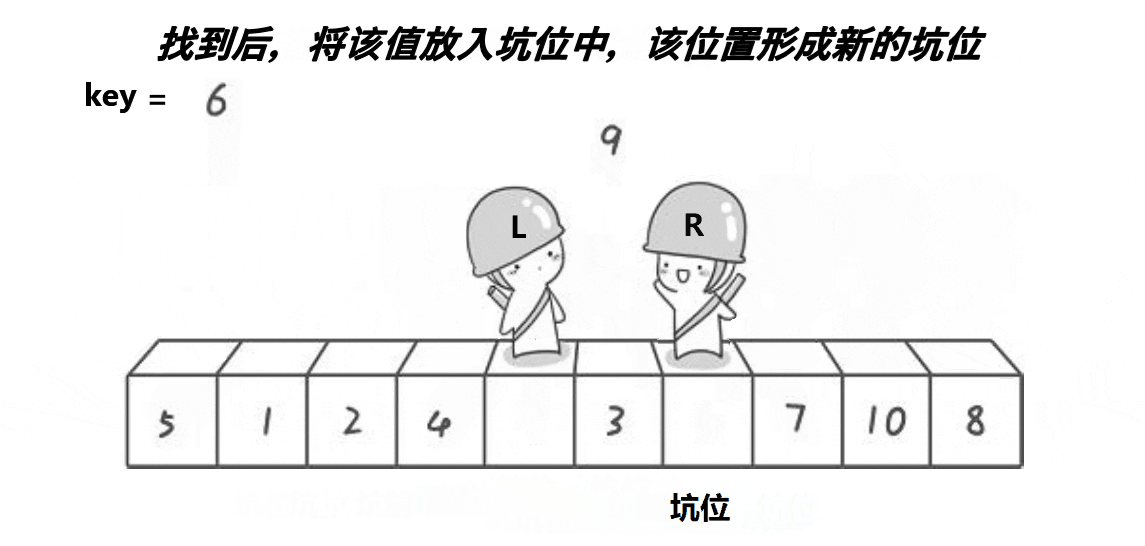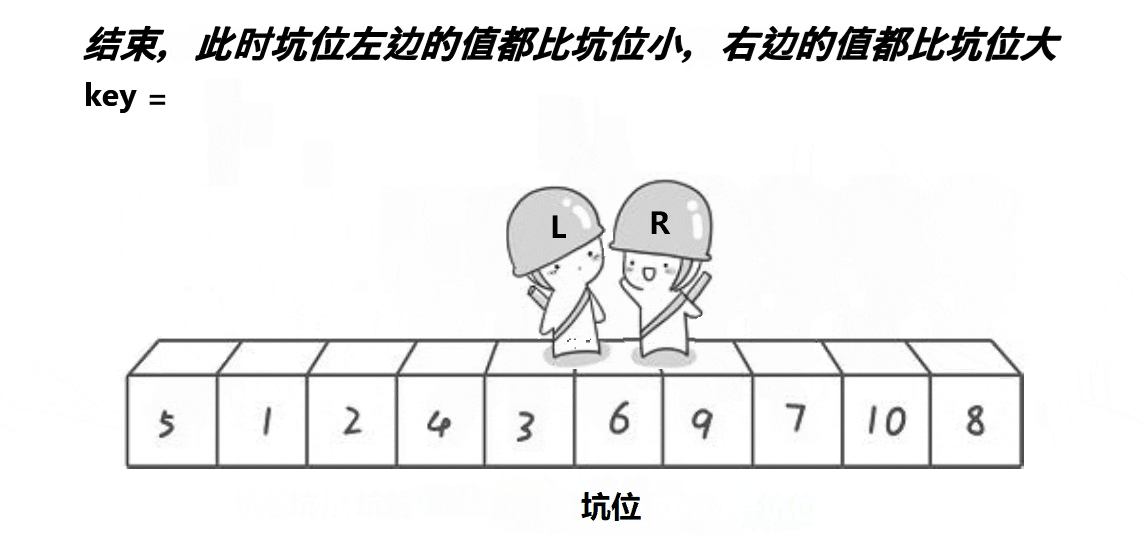
选择一个基准值，仍然通过begin和end指针来操作

首先，我们仍然是从end开始向前找一个小于28的数，找到后直接放在begin的位置，注意这里不是交换，如下图：

箭头所指向的是我们选取的基准值，这时可以理解为它不在这个数列当中，而end对应的位置就出现了一个坑，这时，begin开始向后寻找，找到第一个大于基准值的数后放到end的位置，如下图

此时，begin的位置又会出现一个坑，这时再次让end向前移动继续找第一个小于基准值的数，放到begin的位置，再使begin向后移动找第一个大于基准值的数，重复此操作直到begin和end相遇，这时，把基准值放到该位置。这样，一趟快速排序结束，如下图

 代码实现：

void QuickSort(int* a, int left, int right)
{
	if (right - left <= 1)
	{
		return;
	}
	int key = left;
	int begin = left;
	int pit = left;//坑
	int end = right;
	while (begin < end)
	{
		while (begin < end && a[end] >= a[key])//在右边找到第一个比key小的值
		{
			end--;
		}
		a[pit] = a[end];//放入坑中
		pit = end;//坑更新
		while (begin < end && a[begin] <= a[key])//在左边找到第一个比key大的值
		{
			++begin;
		}
		a[pit] = a[begin];
		pit = begin;
	}
	a[pit] = a[key];//最后将key放入坑中
	QuickSort(a, left, begin-1);
	QuickSort(a, begin+1, right);
}

3、前后指针法

 

前后指针法：
第一步：选最右边的值做key（key是单趟排序后能排到最后该待的位置的数据）
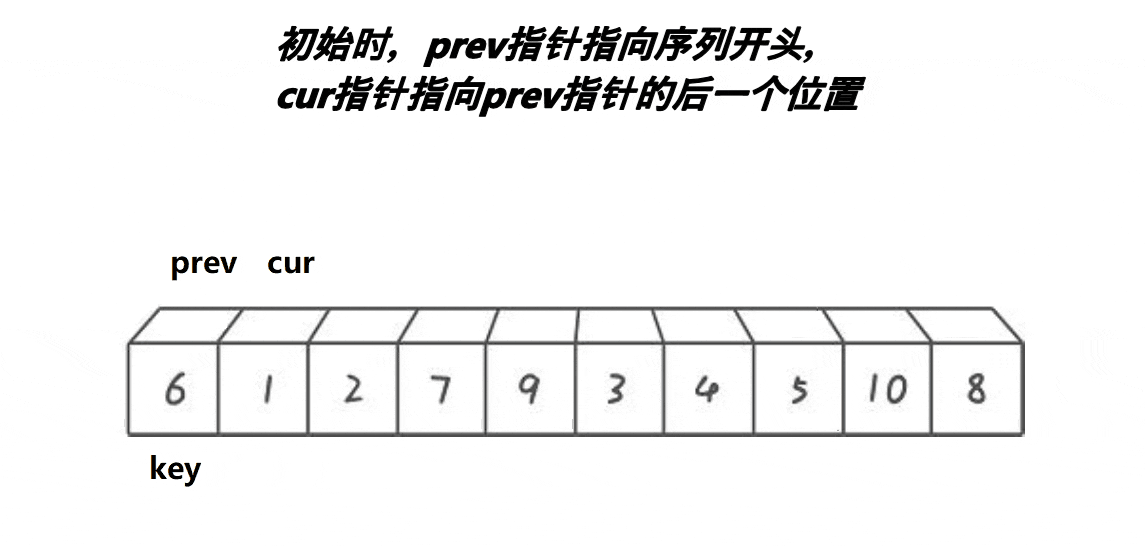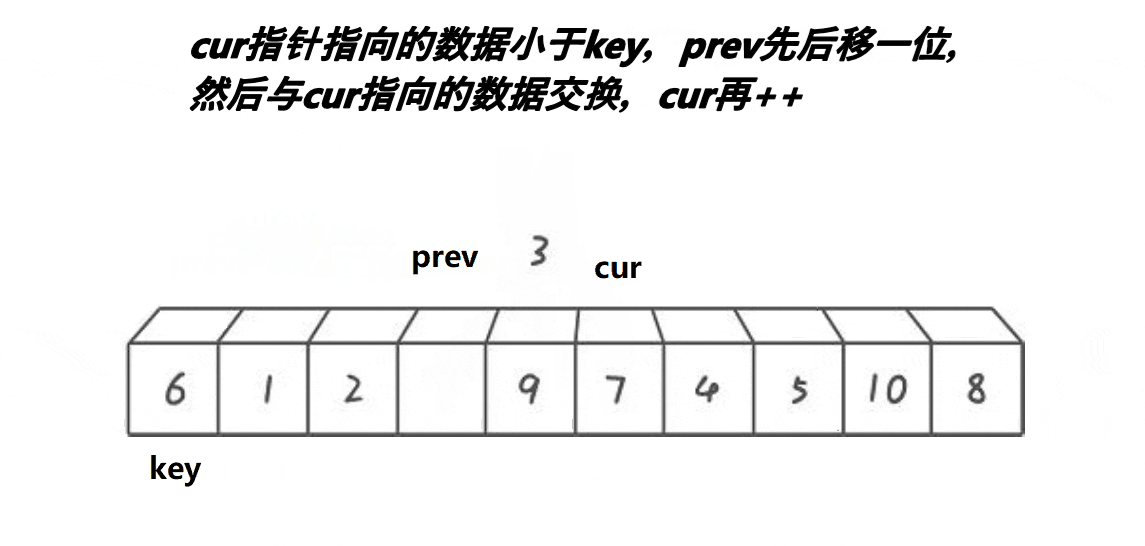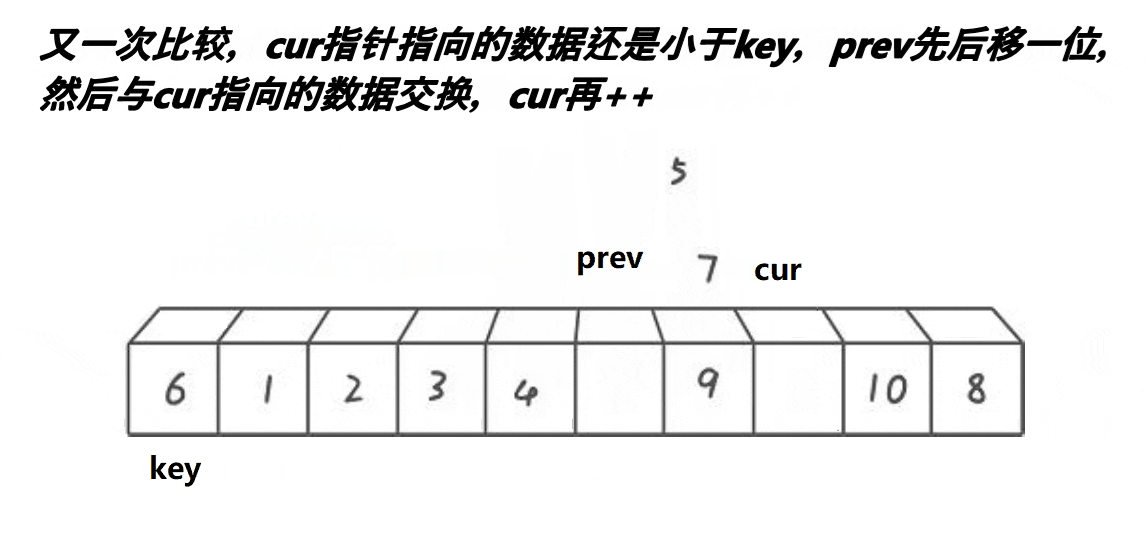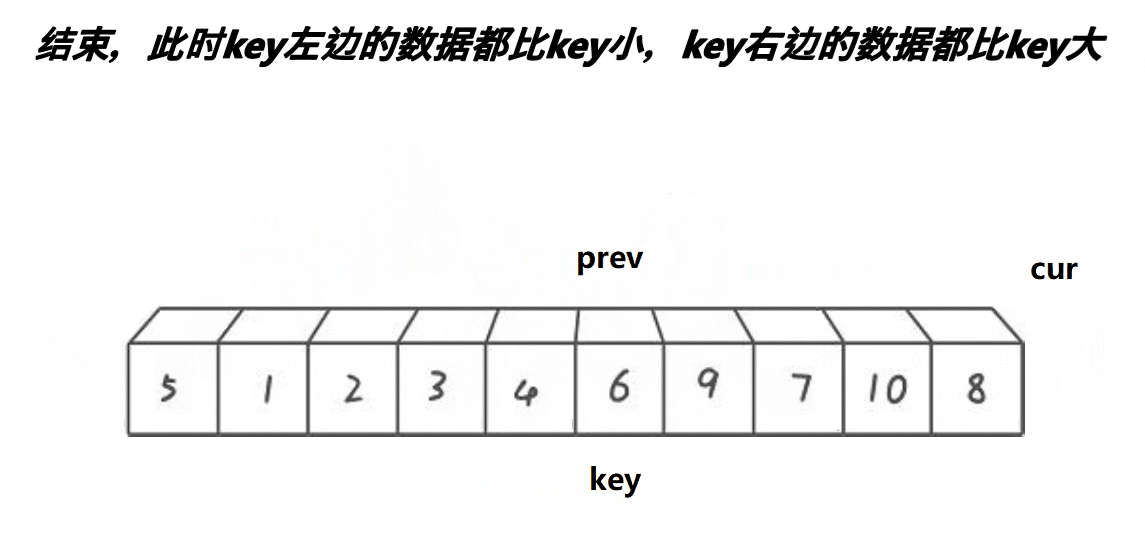
第二步：cur开始找，cur遇到比key小或相等的，cur和prev交换，cur和prev一起向右走。cur遇到比key大的，cur向右走，prev不动。一直循环第二步（若cur走出了数组，结束）

还是先写单趟

 
int key = left;
int pre = left;
int cur = left + 1;
while (cur <= right - left + 1)
{
	if (a[cur] < a[key] && ++pre != cur)//pre加后如果与cur相等为自己与自己交换
	{
		swap(&a[cur], &a[pre]);//交换后要cur++，大于也++，所以直接出判断++
	}
	cur++;
}
swap(&a[key], &a[pre]);

当出现自己于自己交换时可以不用交换，因为交不交换都要cur++所以直接在if后面++ 

整体代码：

 

void QuickSort(int* a, int left, int right)
{
	/*if (right - left <= 1)
	{
		return;
	}*/
	 //小区间优化，不再递归分割排序，减少递归的次数
	if ((right - left + 1) < 10)
	{
		InsertSort(a + left, right - left + 1);//这一定要加left
	}
	else
	{
		int mid = findmid(a, left, right);
		swap(&a[left], &a[mid]);
		int key = left;
		int pre = left;
		int cur = left + 1;
		while (cur <= right - left + 1)
		{
			if (a[cur] < a[key] && ++pre != cur)//pre加后如果与cur相等为自己与自己交换
			{
				swap(&a[cur], &a[pre]);//交换后要cur++，大于也++，所以直接出判断++
			}
			cur++;
		}
		swap(&a[key], &a[pre]);
		int key = pre;
		QuickSort(a, left, key - 1);
		QuickSort(a, key+ 1, right);
	}
}

三、优化：

1、避免重复选择

 插入排序时间复杂度为O（nlogn）（每一层n个值，树的高度为logn）

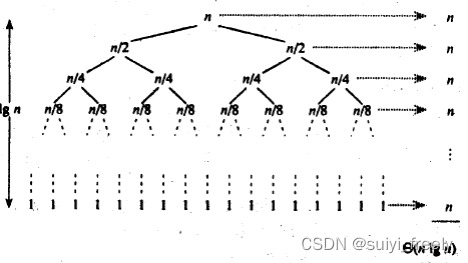
但是对于我们刚刚实现的版本如果一个数列已经排好了，但是代码任然会一个一个比较;

所以我们接下来重点考虑其怎么优化？最佳的答案为三数取中原则：即给定三个数取不大不小的那个，这样会大大减少在循环中比较的次数。从而提高效率：
代码实现：

lfindmid(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	// left midi right
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else // a[left] > a[midi]
	{
		if (a[midi] > a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
void QuickSort(int* a, int left, int right)
{
	if (right - left <= 1)
	{
		return;
	}
	int key = findmid(a, left, right);
	int begin = left;
	int pit = left;//坑
	int end = right;
	while (begin < end)
	{
		while (begin < end && a[end] >= a[key])//在右边找到第一个比key小的值
		{
			end--;
		}
		a[pit] = a[end];
		pit = end;
		while (begin < end && a[begin] <= a[key])//在左边找到第一个比key大的值
		{
			++begin;
		}
		a[pit] = a[begin];
		pit = begin;
	}
	a[pit] = a[key];
	QuickSort(a, left, begin-1);
	QuickSort(a, begin+1, right);
}

2、时间优化

对于一颗树来说最后几层几乎占了大部分的数据，例如：

对于排好五个数如果我们用递归实现则需要递归6次这是非常麻烦的，所以我们最好用插入排序去实现剩余部分的排序：

lfindmid(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	// left midi right
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else // a[left] > a[midi]
	{
		if (a[midi] > a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
void QuickSort(int* a, int left, int right)
{
	if (right - left <= 1)
	{
		return;
	}
	// 小区间优化，不再递归分割排序，减少递归的次数
	if ((right - left + 1) < 10)
	{
		InsertSort(a + left, right - left + 1);//这一定要加left
	}
	int key = findmid(a, left, right);
	int begin = left;
	int pit = left;//坑
	int end = right;
	while (begin < end)
	{
		while (begin < end && a[end] >= a[key])//在右边找到第一个比key小的值
		{
			end--;
		}
		a[pit] = a[end];
		pit = end;
		while (begin < end && a[begin] <= a[key])//在左边找到第一个比key大的值
		{
			++begin;
		}
		a[pit] = a[begin];
		pit = begin;
	}
	a[pit] = a[key];
	QuickSort(a, left, begin-1);
	QuickSort(a, begin+1, right);
}

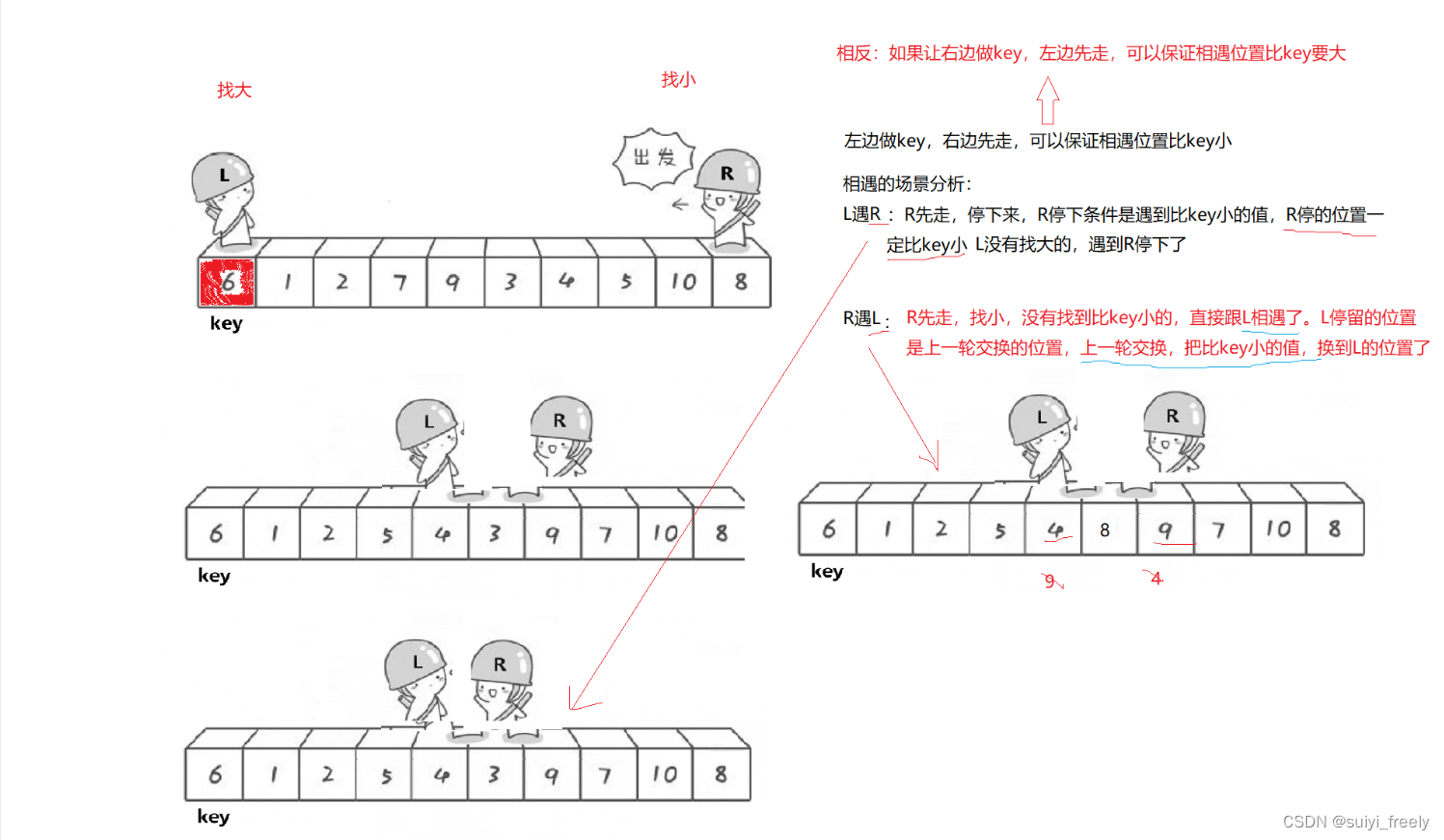
四、hoare版的相关证明：   

hoare版中比较让人难以理解的是为什么最后相遇时值比key小。（其次hoare规定如果让左边做key，那么右边一点要先走），相关证明如下：

 

五、非递归两种实现方法

将递归改为非递归一共有两种办法：
1、是通过栈来模拟实现递归，2、是直接通过循环来实现

而快速排序最好的办法是用栈来模拟实现：

众所周知，栈的特性是先进后出，我们拿数组arr=[5,2,4,7,9,1,3,6]来举栗子。
第一步：我们先把区间的右边界值7进行压栈，然后把区间的左边界值0进行压栈，那我们取出时就可以先取到左边界值，后取到后边界值

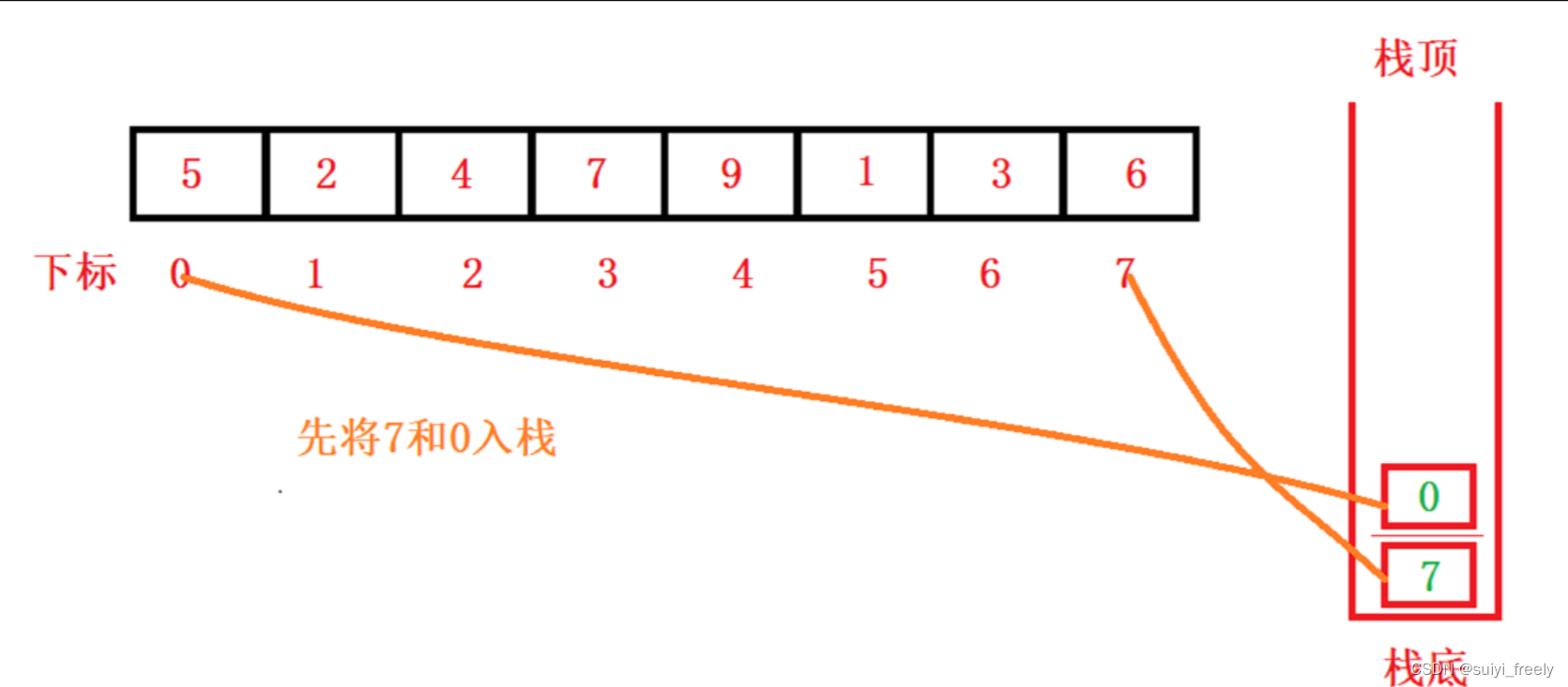
第二步：我们获取栈顶元素，先取到0给left，后取到7给right，进行单趟排序

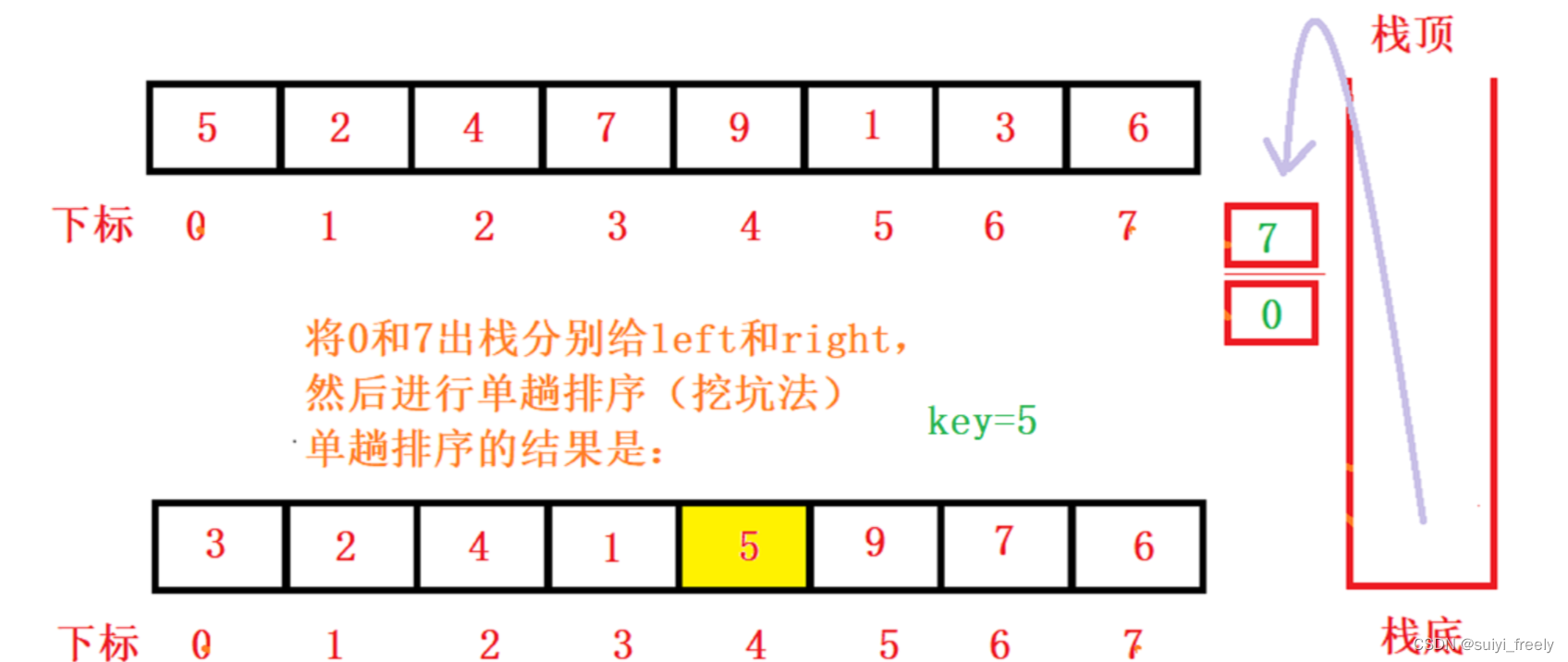
第三步：第一趟排完后，区间被分为左子区间和右子区间。为了先处理左边，所以我们先将右子区间压栈，分别压入7和5，然后压入左子区间，3和0

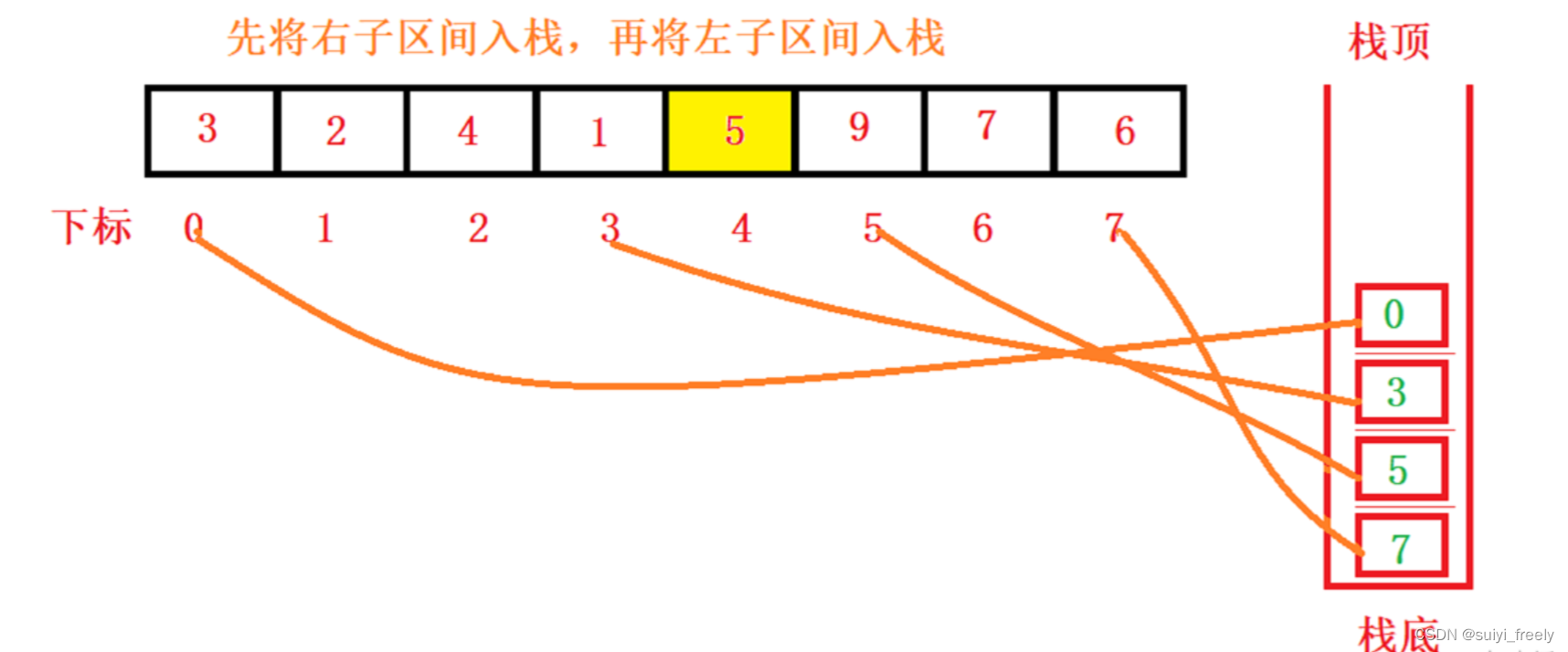
第四步：取出0和3进行单趟排序

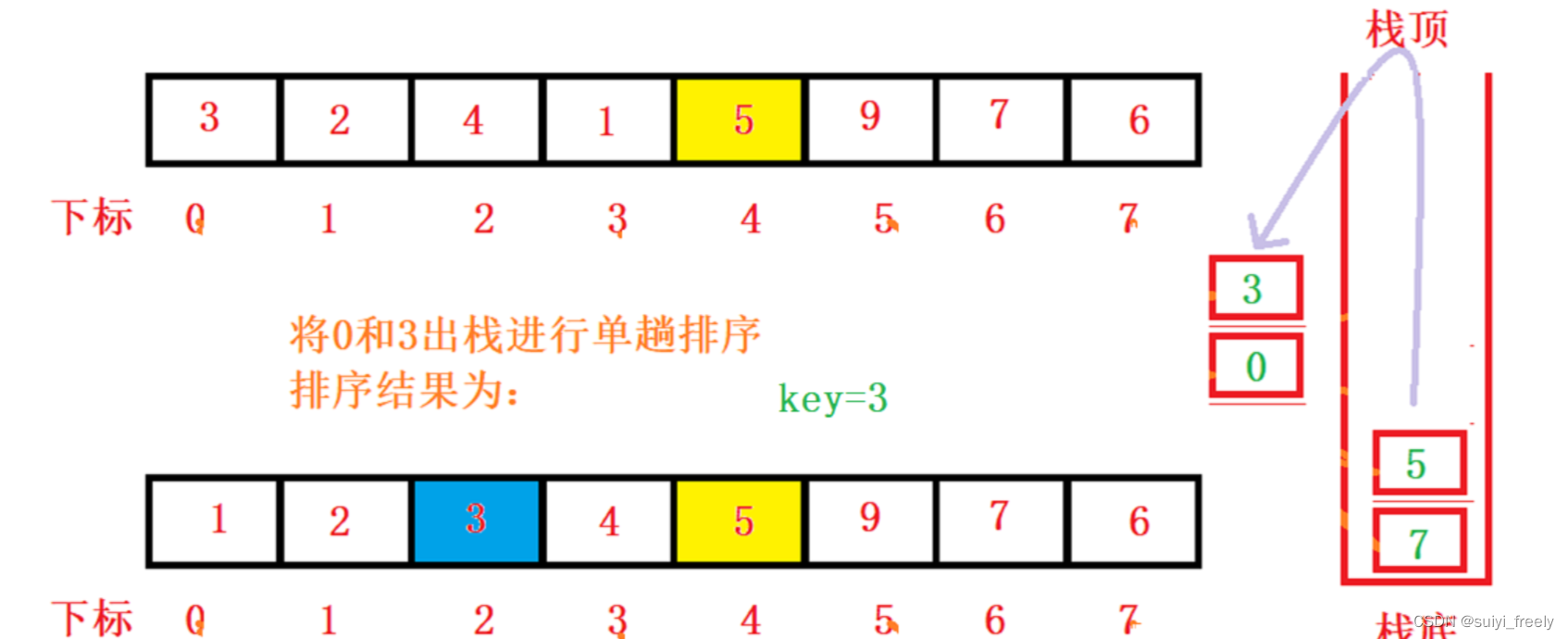
第五步：此时左子区间又被划分为左右两个子区间，但是右子区间只有4一个值，不再压栈，所以只入左子区间，将1和0压栈

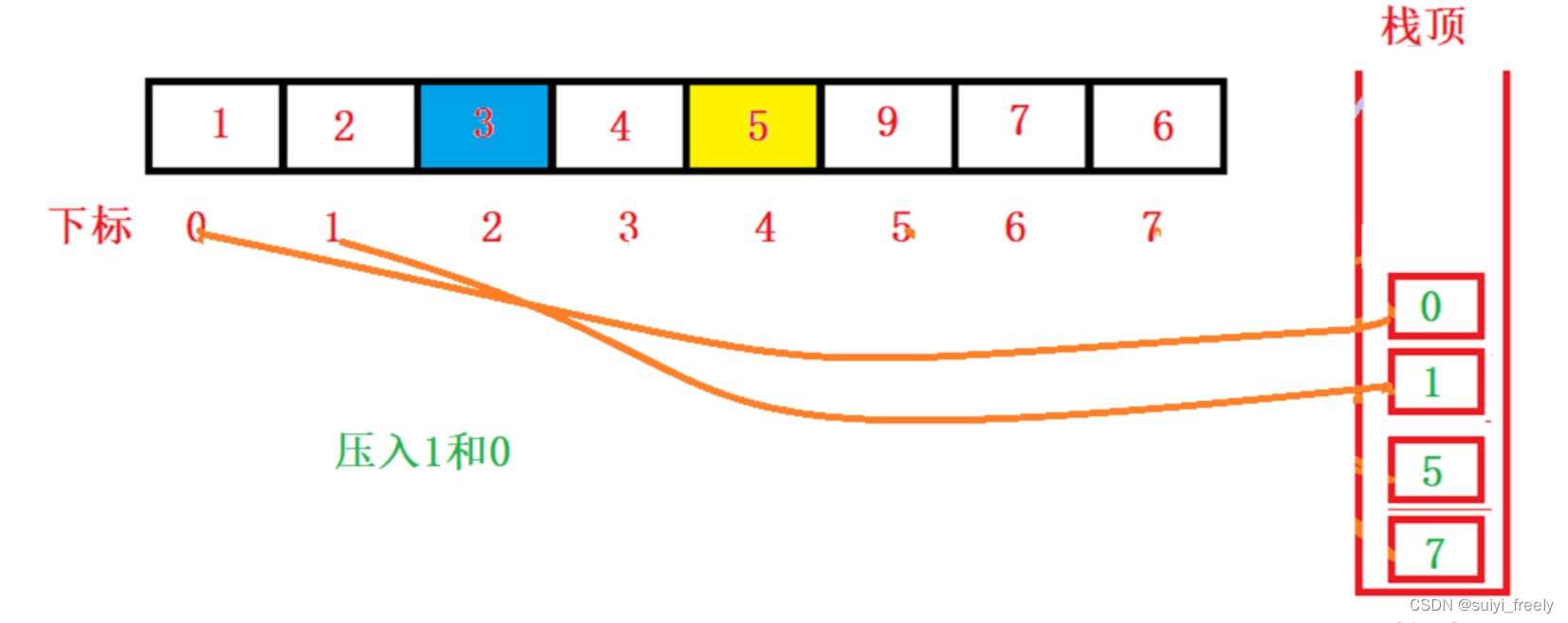
第六步：取出0和1进行单趟排序

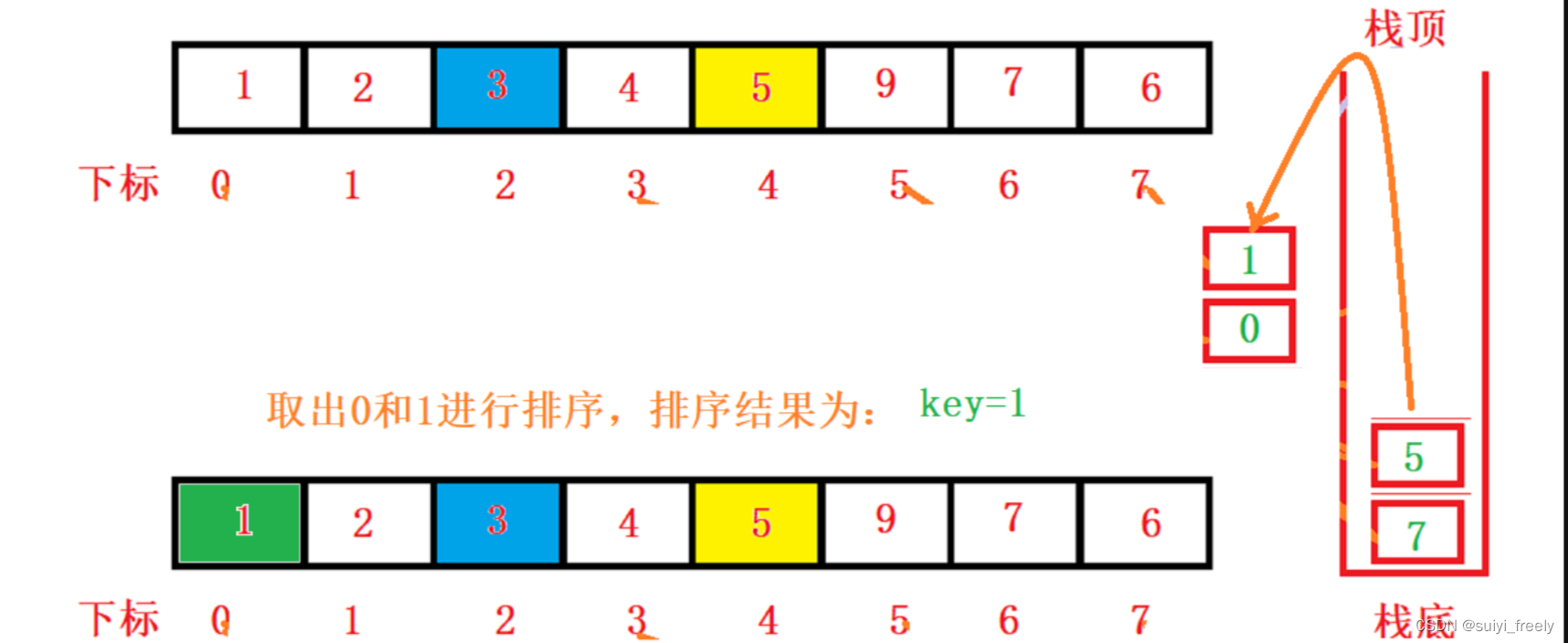
至此，左子区间全部被排完，这时候才可以出5和7排右子区间，这个流程其实和递归是一模一样的，顺序也没变，但解决了递归的致命缺陷——栈溢出。后面的流程就不一一展现了

 

void QuickSortNonR(int* a, int left, int right)
{
	Stack st;
	StackInit(&st);
	StackPush(&st, right);//先入右，再入左
	StackPush(&st, left);
	while (!StackEmpty(&st))//栈为空说明区间排完了
	{
		int begin = StackTop(&st);// 取的时候为先左后右
		StackPop(&st);
		int end = StackTop(&st);
		StackPop(&st);
		int key = PartSort1(a, begin, end);
		if (key + 1 < end)//如果右存在先压右
		{
			StackPush(&st, end);
			StackPush(&st, key + 1);
		}
		if (key - 1 > begin)//如果左存在先压左
		{
			StackPush(&st, key - 1);
			StackPush(&st, begin);
		}
	}
	StackDestroy(&st);
}

那么我们是否可以通过队列来实现呢？当然是可以的只不过将类似前序遍历，改成了层序遍历。

 

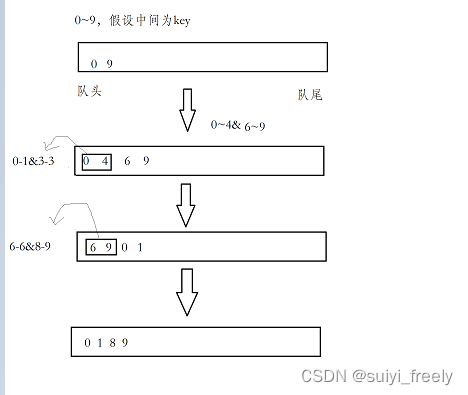
void QuickSortNonR2(int* a, int left, int right)
{
	Queue qe;
	QueueInit(&qe);
	QueuePush(&qe, left);//先进先出先加左边
	QueuePush(&qe, right);
	while (!QueueEmpty(&qe))
	{
		int begin = QueueFront(&qe);
		QueuePop(&qe);
		int end = QueueFront(&qe);
		QueuePop(&qe);
		int key = PartSort1(a, begin, end);
		if (key - 1 > begin)//如果左存在先压左
		{
			QueuePush(&qe, begin);
			QueuePush(&qe, key - 1);
		}
		if (key + 1 < end)//如果右存在先压右
		{
			QueuePush(&qe, key + 1);
			QueuePush(&qe, end);
		}
	}
	QueueDestroy(&qe);
 
}