devbox
木道寻08
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

最短路径---Floyd算法（C++）_最短路径问题c++

作者：木道寻08 | 2024-07-08 02:32:21

赞

踩

最短路径问题c++

Floyd算法的介绍
算法的特点： 
弗洛伊德算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或有向图或负权（但不可存在负权回路)的最短路径问题，同时也被用于计算有向图的传递闭包。

算法的思路

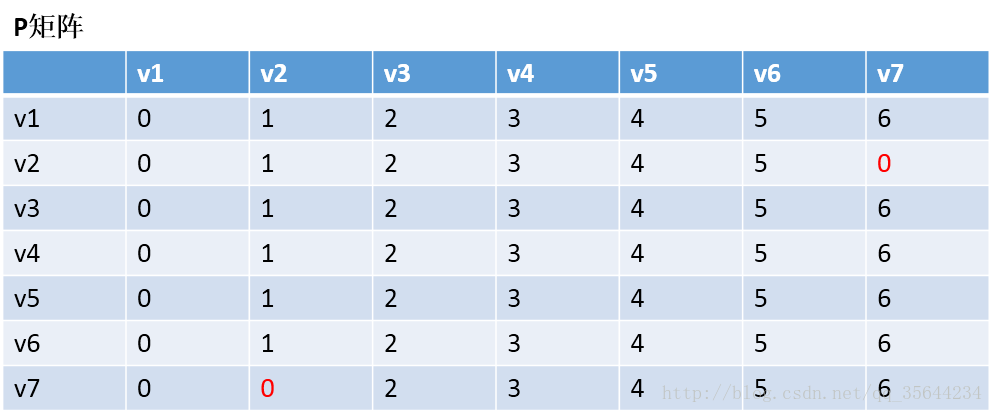
通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入两个矩阵，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素b[i][j]，表示顶点i到顶点j经过了b[i][j]记录的值所表示的顶点。

假设图G中顶点个数为N，则需要对矩阵D和矩阵P进行N次更新。初始时，矩阵D中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞，矩阵P的值为顶点b[i][j]的j的值。 接下来开始，对矩阵D进行N次更新。第1次更新时，如果”a[i][j]的距离” > “a[i][0]+a[0][j]”(a[i][0]+a[0][j]表示”i与j之间经过第1个顶点的距离”)，则更新a[i][j]为”a[i][0]+a[0][j]”,更新b[i][j]=b[i][0]。 同理，第k次更新时，如果”a[i][j]的距离” > “a[i][k-1]+a[k-1][j]”，则更新a[i][j]为”a[i][k-1]+a[k-1][j]”,b[i][j]=b[i][k-1]。更新N次之后，操作完成！

Floyd算法的实例过程

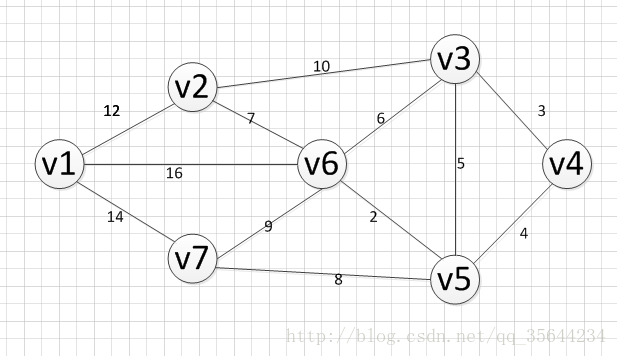
上面，我们已经介绍了算法的思路，如果，你觉得还是不理解，那么通过一个实际的例子，把算法的过程过一遍，你就明白了，如下图，我们求下图的每个点对之间的最短路径的过程如下：

è¿éåå¾çæè¿°

第一步：

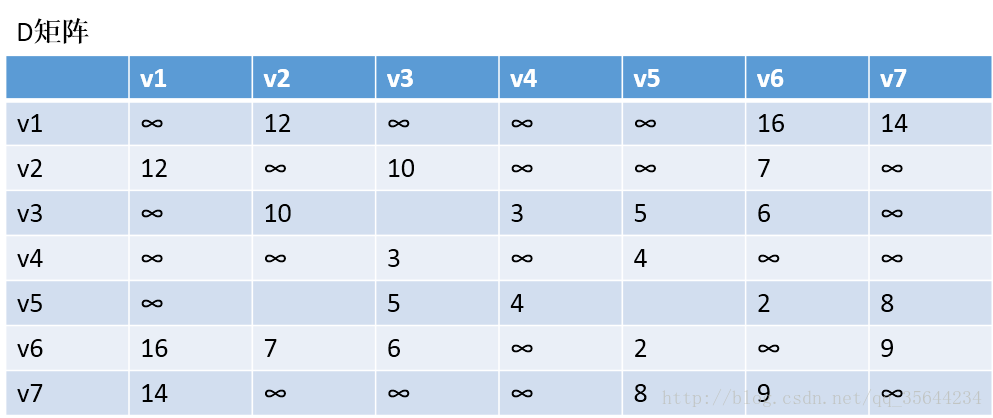
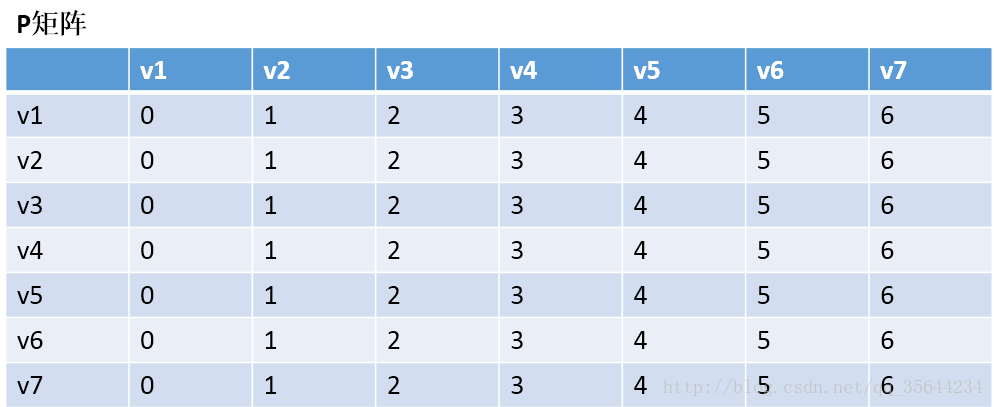
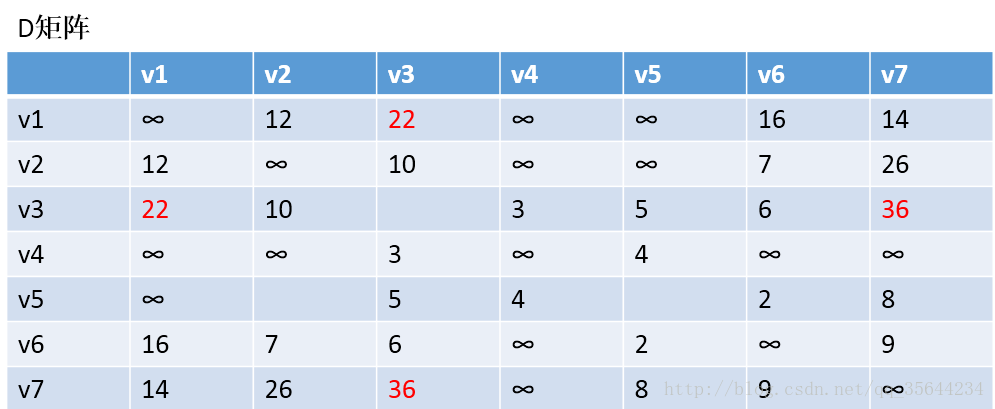
我们先初始化两个矩阵，得到下图两个矩阵： 


、

第二步：

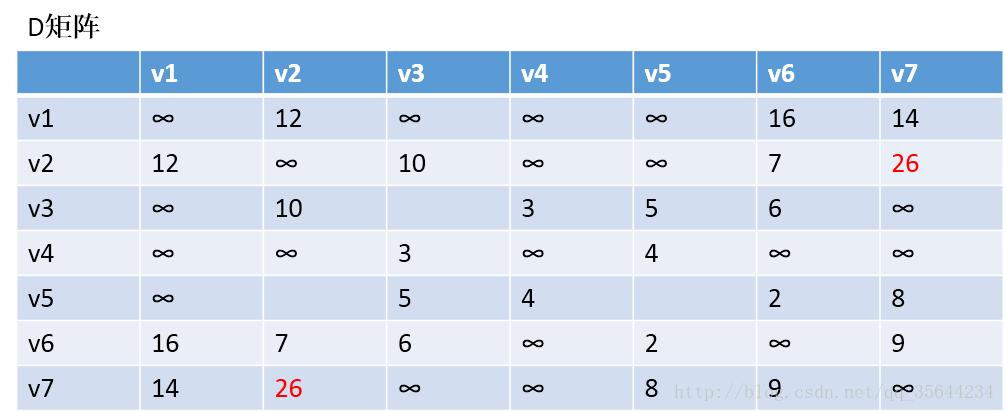
以v1为中阶，更新两个矩阵：发现，a[1][0]+a[0][6] < a[1][6] 和a[6][0]+a[0][1] < a[6][1]，所以我们只需要矩阵D和矩阵P，结果如下：

通过矩阵P，我发现v2–v7的最短路径是：v2–v1–v7

第三步：

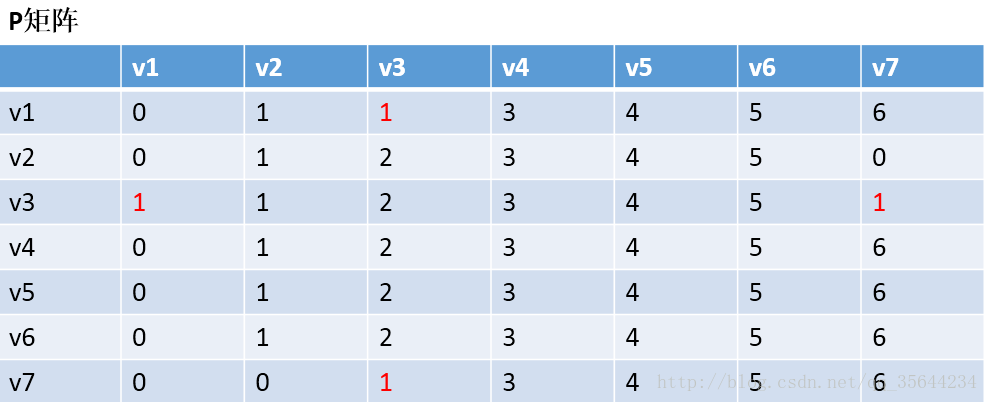
以v2作为中介，来更新我们的两个矩阵，使用同样的原理，扫描整个矩阵，得到如下图的结果：


OK，到这里我们也就应该明白Floyd算法是如何工作的了，他每次都会选择一个中介点，然后，遍历整个矩阵，查找需要更新的值，下面还剩下五步，就不继续演示下去了，理解了方法，我们就可以写代码了。
 

代码：

floyd.h

  1. #ifndef FLOYD_H
  2. #define FLOYD_H
  3.  
  4. #pragma once
  5.  
  6. #include <iostream>
  7. #include <string>
  8. using namespace std;
  9.  
  10. class Graph_DG
  11. {
  12. private:
  13.     int vexnum;  // 图中顶点个数
  14.     int edge;    // 图的边数
  15.     int **arc;   // 邻接矩阵
  16.     int **dis;   // 记录各个顶点最短路径的信息
  17.     int **path;  // 记录各个最短路径
  18.  
  19. public:
  20.     Graph_DG(int v, int e);
  21.     ~Graph_DG();
  22.  
  23.     // 判断每次输入的边是否合法，顶点从1开始编号
  24.     bool check_edge_value(int start, int end);
  25.     void creatGraph(int kind);
  26.     void print();  // 打印邻接矩阵
  27.     void Floyd();
  28.     void print_path();  // 打印最短路径
  29. };
  30.  
  31. #endif // FLOYD_H

 

floyd.cpp

  1. #include "floyd.h"
  2.  
  3. Graph_DG::Graph_DG(int v, int e)
  4. {
  5.     vexnum = v;
  6.     edge = e;
  7.  
  8.     arc = new int*[vexnum];
  9.     dis = new int*[vexnum];
  10.     path = new int*[vexnum];
  11.  
  12.     for (int i = 0; i < vexnum; ++i)
  13.     {
  14.         arc[i] = new int[vexnum];
  15.         dis[i] = new int[vexnum];
  16.         path[i] = new int[vexnum];
  17.  
  18.         for (int j = 0; j < vexnum; ++j)
  19.         {
  20.             // 邻接矩阵初始化为无穷大
  21.             arc[i][j] = INT_MAX;
  22.         }
  23.     }
  24. }
  25.  
  26. Graph_DG::~Graph_DG()
  27. {
  28.     for (int i = 0; i < vexnum; ++i)
  29.     {
  30.         delete [] this->arc[i];
  31.         delete [] this->dis[i];
  32.         delete [] this->path[i];
  33.     }
  34.     delete [] arc;
  35.     delete [] dis;
  36.     delete [] path;
  37. }
  38.  
  39. // 判断我们每次输入的的边的信息是否合法
  40. //顶点从1开始编号
  41. bool Graph_DG::check_edge_value(int start, int end)
  42. {
  43.     if (start < 1 || end < 1 || start > vexnum || end > vexnum)  // Floyd算法，权值可以为负
  44.     {
  45.         return false;
  46.     }
  47.     return true;
  48. }
  49.  
  50. void Graph_DG::creatGraph(int kind)
  51. {
  52.     cout << "请输入每条边的起点和终点（顶点编号从1开始）以及其权重" << endl;
  53.     int start, end, weight;
  54.     int count = 0;
  55.     while (count != edge)
  56.     {
  57.         cin >> start >> end >> weight;
  58.         while (!check_edge_value(start, end))
  59.         {
  60.             cout << "输入的边的信息不合法，请重新输入" << endl;
  61.             cin >> start >> end >> weight;
  62.         }
  63.         arc[start-1][end-1] = weight;
  64.  
  65.         // 无向图添加这一句
  66.         if (kind == 2)
  67.         {
  68.             arc[end-1][start-1] = weight;
  69.         }
  70.         ++count;
  71.     }
  72. }
  73.  
  74. void Graph_DG::print()
  75. {
  76.     cout << "图的邻接矩阵为：" << endl;
  77.     int row = 0;
  78.     int col = 0;
  79.  
  80.     while (row != vexnum)
  81.     {
  82.         col = 0;
  83.         while (col != vexnum)
  84.         {
  85.             if (arc[row][col] == INT_MAX)
  86.             {
  87.                 cout << "∞ ";
  88.             }
  89.             else
  90.             {
  91.                 cout << arc[row][col] << " ";
  92.             }
  93.             ++col;
  94.         }
  95.         cout << endl;
  96.         ++row;
  97.     }
  98. }
  99.  
  100. void Graph_DG::Floyd()
  101. {
  102.     int row, col;
  103.     for (row = 0; row < vexnum; ++row)
  104.     {
  105.         for (col = 0; col < vexnum; ++col)
  106.         {
  107.             // 把矩阵D初始化为邻接矩阵
  108.             dis[row][col] = arc[row][col];
  109.  
  110.             // 矩阵P的初值为各个边的终点顶点下标
  111.             path[row][col] = col;
  112.         }
  113.     }
  114.  
  115.     // 三重循环，用于计算每两个点之间的最短路径.【动态规划的思想】
  116.     int temp, select;
  117.     for (temp = 0; temp < vexnum; ++temp)
  118.     {
  119.         for (row = 0; row < vexnum; ++row)
  120.         {
  121.             for (col = 0; col < vexnum; ++ col)
  122.             {
  123.                 // 为防止溢出，引入一个select值
  124.                 select = (dis[row][temp] == INT_MAX || dis[temp][col] == INT_MAX) ?
  125.                             INT_MAX : dis[row][temp] + dis[temp][col];
  126.                 if (dis[row][col] > select)
  127.                 {
  128.                     // 更新D矩阵
  129.                     dis[row][col] = select;
  130.  
  131.                     // 更新P矩阵
  132.                     path[row][col] = path[row][temp];
  133.                 }
  134.             }
  135.         }
  136.     }
  137. }
  138.  
  139. void Graph_DG::print_path()
  140. {
  141.     cout << "各个顶点对的最短路径：" << endl;
  142.     int row, col, temp;
  143.     for (row = 0; row < vexnum; ++row)
  144.     {
  145.         for (col = row + 1; col < vexnum; ++col)
  146.         {
  147.             cout << "v" << to_string(row + 1) << "---v" << to_string(col + 1) << " weight: "
  148.                  << dis[row][col] << " path: v" << to_string(row + 1);
  149.             temp = path[row][col];
  150.  
  151.             // 循环输出途径的每条路径
  152.             while (temp != col)
  153.             {
  154.                 // path[i][j] = k, 表示从i走到j，第一步需要从i到k
  155.                 // 同理，再从k到j,第一步需要走到path[k][j]
  156.                 cout << "-->v" << to_string(temp + 1);
  157.                 temp = path[temp][col];
  158.             }
  159.             cout << "-->v" << to_string(col + 1) << endl;
  160.         }
  161.         cout << endl;
  162.     }
  163. }
  164.

 

main.cpp

  1. #include <floyd.h>
  2.  
  3. //顶点数和边数的关系是：((Vexnum*(Vexnum - 1)) / 2) < edge
  4. bool check(int vexnum, int edge)
  5. {
  6.     if (vexnum <= 0 || edge <= 0 || (vexnum*(vexnum-1)/2) < edge)
  7.     {
  8.         return false;
  9.     }
  10.     return true;
  11. }
  12.  
  13. int main()
  14. {
  15.     int vexnum, edge, kind;
  16.     cout << "输入图的种类：1代表有向图，2代表无向图" << endl;
  17.     cin >> kind;
  18.     while (1)
  19.     {
  20.         if (kind == 1 || kind == 2)
  21.         {
  22.             break;
  23.         }
  24.         else
  25.         {
  26.             cout << "输入的图的种类编号不合法，请重新输入：1代表有向图，2代表无向图" << endl;
  27.             cin >> kind;
  28.         }
  29.     }
  30.  
  31.     cout << "输入图的顶点个数和边的条数：" << endl;
  32.     cin >> vexnum >> edge;
  33.     while(!check(vexnum, edge))
  34.     {
  35.         cout << "输入的数值不合法，请重新输入" << endl;
  36.         cin >> vexnum >> edge;
  37.     }
  38.  
  39.     Graph_DG graph(vexnum, edge);
  40.     graph.creatGraph(kind);
  41.     graph.print();
  42.     graph.Floyd();
  43.     graph.print_path();
  44.  
  45.     return 0;
  46. }

运行结果：

 

注：

  1. 原文代码中，析构函数部分delete后面没有加 [] ，会出现内存泄漏的情况。
  2. Floyd算法可以对负权值图进行求解，若出现负环，则原问题本身无法求解，因此Floyd算法也可用于检验是否出现负环（初始化所有dis[i][i] = 0，在第三层循环relax结束后，加一个判断dis[i][i]是否为负，若为负则说明存在负环，详细代码可参考下一篇博客）。
  3. 在打印路径部分，对path[i][j]的理解如下：path[i][j] = k, 表示从i走到j，第一步需要从i到k；同理，再从k到j,第一步需要走到path[k][j]。
  4. Floyd算法本身采用的是动态规划的思想。

 

参考资料：https://blog.csdn.net/qq_35644234/article/details/60875818

本文内容由网友自发贡献，转载请注明出处：【wpsshop博客】
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号