数据结构——图的两种遍历【深度优先遍历-广度优先遍历】的区别用法_深度优先遍历和广度优先遍历对比

https://www.cnblogs.com/nr-zhang/p/11236369.html
1

 

　深度优先遍历(Depth First Search)的主要思想是：

A：首先以一个未被访问过的顶点作为起始顶点

沿当前顶点的边走到未访问过的顶点

B：当没有未访问过的顶点时则回到上一个顶点

继续试探别的顶点，直至所有的顶点都被访问过

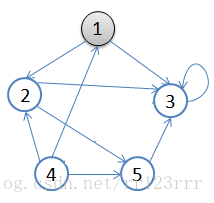
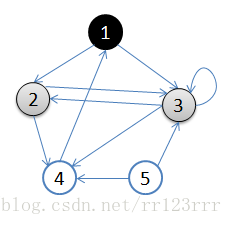
2.图表达流程

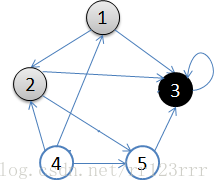
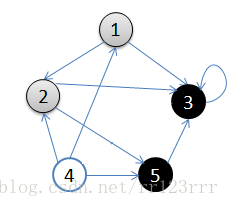
A:1.从v = 顶点1开始出发，先访问顶点1 

B:2.按深度优先搜索递归访问v的某个未被访问的邻接点2

C:顶点2结束后，应该访问3或5中的某一个

D:这里为顶点3，此时顶点3不再有出度，因此回溯到顶点2

E:再访问顶点2的另一个邻接点5，由于顶点5的唯一一条边的弧头为3，已经访问了

F:所以此时继续回溯到顶点1，找顶点1的其他邻接点。

 

举例：

上图可以用邻接矩阵来表示为：

int maze[][] = {
    { 0, 1, 1, 0, 0 },
    { 0, 0, 1, 0, 1 },
    { 0, 0, 1, 0, 0 },
    { 1, 1, 0, 0, 1 },
    { 0, 0, 1, 0, 0 }
};
1
2
3
4
5
6
7

代码实现：

具体的代码如下:

import java.util.LinkedList;
import classEnhance.EnhanceModual;
 
public class DepthFirst extends EnhanceModual {
 
    @Override
    public void internalEntrance() {
        // TODO Auto-generated method stub
        int maze[][] = { { 0, 1, 1, 0, 0 }, { 0, 0, 1, 0, 1 }, { 0, 0, 1, 0, 0 }, { 1, 1, 0, 0, 1 },
                { 0, 0, 1, 0, 0 } };
 
        dfs(maze, 1);
 
    }
 
    public void dfs(int[][] adjacentArr, int start) {
        int nodeNum = adjacentArr.length;
        if (start <= 0 || start > nodeNum || (nodeNum == 1 && start != 1)) {
            System.out.println("Wrong input ！");
            return;
        } else if (nodeNum == 1 && start == 1) {
            System.out.println(adjacentArr[0][0]);
            return;
        }
 
        int[] visited = new int[nodeNum + 1];//0表示结点尚未入栈，也未访问
        LinkedList<Integer> stack = new LinkedList<Integer>();
        stack.push(start);
        visited[start] = 1;//1表示入栈
 
        while (!stack.isEmpty()) {
            int nodeIndex = stack.peek();
            boolean flag = false;
            if(visited[nodeIndex] != 2){
                System.out.println(nodeIndex);
                visited[nodeIndex] = 2;//2表示结点被访问
            }
 
            //沿某一条路径走到无邻接点的顶点
            for (int i = 0; i < nodeNum; i++) {
                if (adjacentArr[nodeIndex - 1][i] == 1 && visited[i + 1] == 0) {
                    flag = true;
                    stack.push(i + 1);
                    visited[i + 1] = 1;
                    break;//这里的break不能掉！！！！
                }
            }
 
            //回溯
            if(!flag){
                int visitedNodeIndex = stack.pop();
            }
 
        }
    }
 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

 

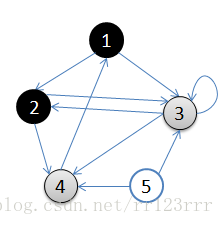
3.对于连通图

A:它从图中某个顶点 触发，访问此顶点

B:然后从  的未被访问的邻接点出发深度优先遍历图

C:直至图中所有和 有路径相通的顶点都被访问到

4.对于非连通图

只需要对它的连通分量分别进行深度优先遍历

A:即在先前一个顶点进行一次深度优先遍历后

B:若图中尚未有顶点未被访问

则另选图中一个未曾被访问的顶点作为起始点

C:重复上述过程，直至图中所有顶点都被访问到为止

5.深度优先搜索

就是选择一个顶点开始走

期间对于走过的顶点就不在访问，走其他未被访问的

一直走到无路可走

若此时还有顶点未走过，选择一个，重复上述过程

6.对无向图的深度优先遍历图解

以下"无向图"为例：

对上无向图进行深度优先遍历，从A开始：

第1步：访问A。

第2步：访问B(A的邻接点)。 在第1步访问A之后，接下来应该访问的是A的邻接点，即"B,D,F"中的一个。但在本文的实现中，顶点ABCDEFGH是按照顺序存储，B在"D和F"的前面，因此，先访问B。

第3步：访问G(B的邻接点)。 和B相连只有"G"(A已经访问过了)  

第4步：访问E(G的邻接点)。 在第3步访问了B的邻接点G之后，接下来应该访问G的邻接点，即"E和H"中一个(B已经被访问过，就不算在内)。而由于E在H之前，先访问E。

第5步：访问C(E的邻接点)。 和E相连只有"C"(G已经访问过了)。

第6步：访问D(C的邻接点)。 

第7步：访问H。因为D没有未被访问的邻接点；因此，一直回溯到访问G的另一个邻接点H。

第8步：访问(H的邻接点)F。

因此访问顺序是：A -> B -> G -> E -> C -> D -> H -> F

7.对有向图的深度优先遍历

有向图的深优先遍历图解：

对上有向图进行深度优先遍历，从A开始：

第1步：访问A。

第2步：访问(A的出度对应的字母)B。 在第1步访问A之后，接下来应该访问的是A的出度对应字母，即"B,C,F"中的一个。但在本文的实现中，顶点ABCDEFGH是按照顺序存储，B在"C和F"的前面，因此，先访问B。

第3步：访问(B的出度对应的字母)F。 B的出度对应字母只有F。 

第4步：访问H(F的出度对应的字母)。 F的出度对应字母只有H。 

第5步：访问(H的出度对应的字母)G。

第6步：访问(G的出度对应字母)E。 在第5步访问G之后，接下来应该访问的是G的出度对应字母，即"B,C,E"中的一个。但在本文的实现中，顶点B已经访问了，由于C在E前面，所以先访问C。

第7步：访问(C的出度对应的字母)D。

第8步：访问(C的出度对应字母)D。 在第7步访问C之后，接下来应该访问的是C的出度对应字母，即"B,D"中的一个。但在本文的实现中，顶点B已经访问了，所以访问D。

第9步：访问E。D无出度，所以一直回溯到G对应的另一个出度E。

因此访问顺序是：A -> B -> F -> H -> G -> C -> D -> E

 

二：广度优先遍历

1.定义 

又称为 广度优先搜索，简称 BFS

广度优先遍历(Depth First Search)的主要思想是：类似于树的层序遍历

https://www.cnblogs.com/nr-zhang/p/11236369.html
1

 

A:广度优先搜索是按层来处理顶点

B:距离开始点最近的那些顶点首先被访问

C:而最远的那些顶点则最后被访问

2.搜索步骤

A ：首先选择一个顶点作为起始顶点，并将其染成灰色，其余顶点为白色。 
B：将起始顶点放入队列中。 
C：从队列首部选出一个顶点

并找出所有与之邻接的顶点

将找到的邻接顶点放入队列尾部

将已访问过顶点涂成黑色，没访问过的顶点是白色

如果顶点的颜色是灰色，表示已经发现并且放入了队列

如果顶点的颜色是白色，表示还没有发现 
D：按照同样的方法处理队列中的下一个顶点。 
基本就是出队的顶点变成黑色，在队列里的是灰色，还没入队的是白色。  

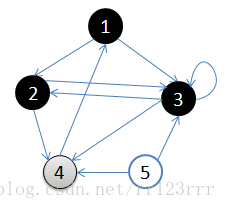
3.图表达流程

用一副图来表达这个流程如下：

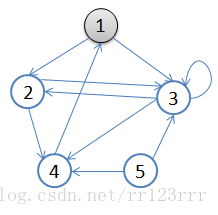
A:初始状态，从顶点1开始，队列={1} 

B:访问1的邻接顶点，1出队变黑，2,3入队，队列={2,3,} 

C:访问2的邻接顶点，2出队，4入队，队列={3,4} 

D:访问3的邻接顶点，3出队，队列={4} 

E:5.访问4的邻接顶点，4出队，队列={ 空} 

从顶点1开始进行广度优先搜索： 

 初始状态，从顶点1开始，队列={1} 
  访问1的邻接顶点，1出队变黑，2,3入队，队列={2,3,} 
  访问2的邻接顶点，2出队，4入队，队列={3,4} 
  访问3的邻接顶点，3出队，队列={4} 
  访问4的邻接顶点，4出队，队列={ 空} 
  顶点5对于1来说不可达
1
2
3
4
5
6

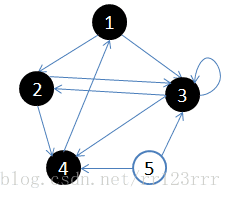
举例：

上面图可以用如下邻接矩阵来表示：

int maze[][] = {
    { 0, 1, 1, 0, 0 },
    { 0, 0, 1, 1, 0 },
    { 0, 1, 1, 1, 0 },
    { 1, 0, 0, 0, 0 },
    { 0, 0, 1, 1, 0 }
};
1
2
3
4
5
6
7

代码实现：

具体的代码如下，这段代码有两个功能，bfs（）函数求出从某顶点出发的搜索结果，minPath（）函数求从某一顶点出发到另一顶点的最短距离：

import java.util.LinkedList;
 
import classEnhance.EnhanceModual;
 
public class BreadthFirst extends EnhanceModual {
 
    @Override
    public void internalEntrance() {
        // TODO Auto-generated method stub
        int maze[][] = {
            { 0, 1, 1, 0, 0 }, 
            { 0, 0, 1, 1, 0 }, 
            { 0, 1, 1, 1, 0 },
            { 1, 0, 0, 0, 0 },
            { 0, 0, 1, 1, 0 }
        };
 
        bfs(maze, 5);//从顶点5开始搜索图
 
        int start = 5;
        int[] result = minPath(maze, start);
        for(int i = 1; i < result.length; i++){
            if(result[i] !=5 ){
                System.out.println("从顶点" + start +"到顶点" + i + "的最短距离为：" + result[i]);
            }else{
                System.out.println("从顶点" + start +"到顶点" + i + "不可达");
            }
        }
    }
 
    public void bfs(int[][] adjacentArr, int start) {
        int nodeNum = adjacentArr.length;
        if (start <= 0 || start > nodeNum || (nodeNum == 1 && start != 1)) {
            System.out.println("Wrong input ！");
            return;
        } else if (nodeNum == 1 && start == 1) {
            System.out.println(adjacentArr[0][0]);
            return;
        }
 
        int[] visited = new int[nodeNum + 1];//0表示顶点尚未入队，也未访问，注意这里位置0空出来了
        LinkedList<Integer> queue = new LinkedList<Integer>();
        queue.offer(start);
        visited[start] = 1;//1表示入队
 
        while (!queue.isEmpty()) {
            int nodeIndex = queue.poll();
            System.out.println(nodeIndex);
            visited[nodeIndex] = 2;//2表示顶点被访问
 
            for (int i = 0; i < nodeNum; i++) {
                if (adjacentArr[nodeIndex - 1][i] == 1 && visited[i + 1] == 0) {
                    queue.offer(i + 1);
                    visited[i + 1] = 1;
                }
            }
        }
    }
 
    /*
     * 从start顶点出发，到图里各个顶点的最短路径
     */
    public int[] minPath(int[][] adjacentArr, int start) {
 
        int nodeNum = adjacentArr.length;
 
        LinkedList<Integer> queue = new LinkedList<Integer>();
        queue.offer(start);
        int path = 0;
        int[] nodePath = new int[nodeNum + 1];
        for (int i = 0; i < nodePath.length; i++) {
            nodePath[i] = nodeNum;
        }
        nodePath[start] = 0;
 
        int incount = 1;
        int outcount = 0;
        int tempcount = 0;
 
        while (path < nodeNum) {
            path++;
            while (incount > outcount) {
                int nodeIndex = queue.poll();
                outcount++;
 
                for (int i = 0; i < nodeNum; i++) {
                    if (adjacentArr[nodeIndex - 1][i] == 1 && nodePath[i + 1] == nodeNum) {
                        queue.offer(i + 1);
                        tempcount++;
                        nodePath[i + 1] = path;
                    }
                }
            }
 
            incount = tempcount;
            tempcount = 0;
            outcount = 0;
        }
 
        return nodePath;
    }
 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103

运行结果：

//5
//3
//4
//2
//1
//从顶点5到顶点1的最短距离为：2
//从顶点5到顶点2的最短距离为：2
//从顶点5到顶点3的最短距离为：1
//从顶点5到顶点4的最短距离为：1
//从顶点5到顶点5的最短距离为：0
1
2
3
4
5
6
7
8
9
10

 

4.对无向图的广度优先遍历图解

A:从A开始，有4个邻接点，“B，C，D，F”，这是第二层；

B:在分别从B，C，D，F开始找他们的邻接点，为第三层。以此类推。

因此访问顺序是：A -> B -> C -> D -> F -> G -> E -> H

5.对有向图的广度优先遍历图解

因此访问顺序是：A -> B -> C -> F -> D -> H -> G -> E

 

三：异同

1.同

深度优先遍历与广度优先遍历算法在时间复杂度上是一样的

2.异

不同之处仅仅在于对顶点访问的顺序不同

A:深度优先

更适合目标比较明确，以找到目标为主要目的的情况

 

B:而广度优

先更适合在不断扩大遍历范围时找到相对最优解的情况

参考地址：

1.图的深度优先遍历(DFS)和广度优先遍历(BFS)算法分析

https://www.cnblogs.com/zxrxzw/p/11528482.html

2.图的深度优先遍历和广度优先遍历

https://www.cnblogs.com/nr-zhang/p/11236369.html

3.深度优先遍历(DFS)和广度优先遍历(BFS)

https://blog.csdn.net/gqg_guan/article/details/127637502

转载:https://liuxinlei.blog.csdn.net/article/details/104258892