一起来学自然语言处理----学习分类文本（决策树、朴素贝叶斯）_决策树文本分类csdn

  模式识别是自然语言处理的一个核心部分。以-ed 结尾的词往往是过去时态动词。频繁使用 will是新闻文本的暗示。这些可观察到的模式——词的结构和词频——恰好与特定方面的含义关联，如：时态和主题。但我们怎么知道从哪里开始寻找，形式的哪一方面关联含义的哪一方面？我们将在这一节进行讲解。

有监督分类

  分类是为给定的输入选择正确的类标签的任务。在基本的分类任务中，每个输入被认为是与所有其它输入隔离的，并且标签集是预先定义的。这里是分类任务的一些例子：
� 判断一封电子邮件是否是垃圾邮件。
� 从一个固定的主题领域列表中，如“体育”、“技术”和“政治”，决定新闻报道的主题是什么。
� 决定词 bank 给定的出现是用来指河的坡岸、一个金融机构、向一边倾斜的动作还是在金融机构里的存储行为。
  基本的分类任务有许多有趣的变种。例如：在多类分类中，每个实例可以分配多个标签；在开放性分类中，标签集是事先没有定义的；在序列分类中，一个输入链表作为一个整体分类。
  如果分类的建立基于包含每个输入的正确标签的训练语料，被称为有监督分类。流程图如下：

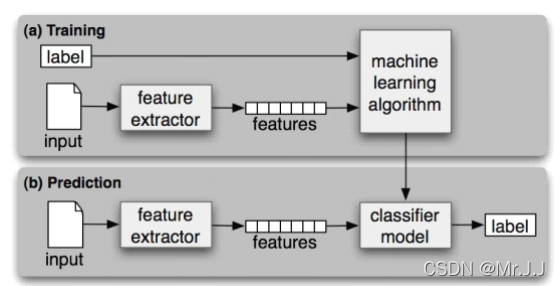
1. 性别鉴定

  通常男性和女性的名字有一些鲜明的特点。以 a，e 和 i 结尾的很可能是女性，而以 k，o，r，s 结尾的很可能是男性。让我们建立一个分类器更精确地模拟这些差异。
  创建一个分类器的第一步是决定输入的什么样的特征是相关的，以及如何为那些特征编 码。在这个例中，我们一开始只是寻找一个给定的名称的最后一个字母。以下特征提取器函数建立一个字典，包含有关给定名称的相关信息。
  接下来，我们使用特征提取器处理名称数据，并划分特征集的结果链表为一个训练集和一个测试集。训练集用于训练一个新的“朴素贝叶斯”分类器，这里并不需要了解朴素贝叶斯的内容，后面会讲解。
  接着我们测试几个新名字，检测分类器输出结果，并在测试集上计算分类器的准确度。
  最后，我们可以检查分类器，确定哪些特征对于区分名字的性别是最有效的。
示例代码：

# 构建一个特征提取器，返回最后一个字母的字典
def gender_features(word):
    return {'last_letter': word[-1]}

# 数据集分测试和训练集
from nltk.corpus import names
import random
import nltk
names = ([(name, 'male') for name in names.words('male.txt')] +
        [(name, 'female') for name in names.words('female.txt')])
# shuffle() 方法将序列的所有元素随机排序。该函数没有返回值，会直接在原容器中乱序。
random.shuffle(names)
featuresets = [(gender_features(n), g) for (n,g) in names]
train_set, test_set = featuresets[500:], featuresets[:500]
# 构建朴素贝叶斯分类器
classifier = nltk.NaiveBayesClassifier.train(train_set)
# 测试新数据
classifier.classify(gender_features('Neo'))
'male'
# 计算测试集上的评分
print (nltk.classify.accuracy(classifier, test_set))
0.764
# 确定哪些特征对于区分名字的性别是最有效的。
classifier.show_most_informative_features(5)
Most Informative Features
             last_letter = 'k'              male : female =     73.6 : 1.0
             last_letter = 'a'            female : male   =     38.5 : 1.0
             last_letter = 'v'              male : female =     17.4 : 1.0
             last_letter = 'f'              male : female =     17.2 : 1.0
             last_letter = 'p'              male : female =     11.8 : 1.0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

  在处理大型语料库时，构建一个包含每一个实例的特征的单独的链表会使用大量的内存。在这些情况下，使用函数 nltk.classify.apply_features，返回一个行为像一个链表而不会在内存存储所有特征集的对象。

from nltk.classify import apply_features
train_set = apply_features(gender_features, names[500:])
test_set = apply_features(gender_features, names[:500])
1
2
3

2. 选择正确的特征

  选择相关的特征，并决定如何为一个学习方法编码它们，这对学习方法提取一个好的模型可以产生巨大的影响。建立一个分类器的很多有趣的工作之一是找出哪些特征可能是相关的，以及我们如何能够表示它们。虽然使用相当简单而明显的特征集往往可以得到像样的性能，但是使用精心构建的基于对当前任务的透彻理解的特征，通常会显著提高收益。
  典型地，特征提取通过反复试验和错误的过程建立的，由哪些信息是与问题相关的直觉指引的。它通常以“厨房水槽”的方法开始，包括你能想到的所有特征，然后检查哪些特征是实际有用的。
  然而，你要用于一个给定的学习算法的特征的数目是有限的——如果你提供太多的特征，那么该算法将高度依赖你的训练数据的特，性而一般化到新的例子的效果不会很好。这个问题被称为过拟合，当运作在小训练集上时尤其会有问题。
  一旦初始特征集被选定，完善特征集的一个非常有成效的方法是错误分析。首先，我们增加一个验证集。训练集用于训练模型，验证集用于进行错误分析，测试集用于系统的最终评估。

3. 文档分类

  前面我们看到了语料库的几个例子，那里文档已经按类别标记。使用这些语料库，我们可以建立分类器，自动给新文档添加适当的类别标签。首先，我们构造一个标记了相应类别的文档清单。对于这个例子，我们选择电影评论语料库，将每个评论归类为正面或负面。

# 构建数据集
from nltk.corpus import movie_reviews
# 用对应标签和标签对应文档包含的单词构建数据集
documents = [(list(movie_reviews.words(fileid)), category)
	# 分类分为正面和负面
    for category in movie_reviews.categories()
    # 获取对应标签下的评论
    for fileid in movie_reviews.fileids(category)]
# 给数据集重新随机排序
random.shuffle(documents)
1
2
3
4
5
6
7
8
9
10

  接下来，我们为文档定义一个特征提取器，这样分类器就会知道哪些方面的数据应注意。对于文档主题识别，我们可以为每个词定义一个特性表示该文档是否包含这个词。为了限制分类器需要处理的特征的数目，我们一开始构建一个整个语料库中前 2000个最频繁词的链表。然后，定义一个特征提取器，简单地检查这些词是否在一个给定的文档中。

# 所有的单词的频率分布
all_words = nltk.FreqDist(w.lower() for w in movie_reviews.words())
# 获取前2000个
word_features = list(all_words.keys())[:2000]
# 自定义的特征提取器
def document_features(document):
    document_words = set(document)
    features = {}
    for word in word_features:
    # 检查一个词是否在一个集合中出现比检查它是否在一个链表中出现要快的多
        features['contains(%s)' % word] = (word in document_words)
    return features
1
2
3
4
5
6
7
8
9
10
11
12

  现在，我们已经定义了我们的特征提取器，可以用它来训练一个分类器，为新的电影评论加标签。为了检查产生的分类器可靠性如何，我们在测试集上计算其准确性。再一次的，我们可以使用 show_most_informative_features()来找出哪些特征是分类器发现最有信息量的。

# 使用特征提取器构建数据集
featuresets = [(document_features(d), c) for (d,c) in documents]
# 数据分测试、训练集
train_set, test_set = featuresets[100:], featuresets[:100]
# 构建朴素贝叶斯分类器
classifier = nltk.NaiveBayesClassifier.train(train_set)
# 输出分类器再测试集上的准确率
print (nltk.classify.accuracy(classifier, test_set))
0.82
# 输出分类器最重要的5个特征
classifier.show_most_informative_features(5)

Most Informative Features
           contains(ugh) = True              neg : pos    =      9.8 : 1.0
     contains(atrocious) = True              neg : pos    =      7.1 : 1.0
        contains(shoddy) = True              neg : pos    =      7.1 : 1.0
 contains(unimaginative) = True              neg : pos    =      7.1 : 1.0
         contains(kudos) = True              pos : neg    =      6.5 : 1.0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

评估

  为了决定一个分类模型是否准确地捕捉了模式，我们必须评估该模型。评估的结果对于决定模型是多么值得信赖以及我们如何使用它是非常重要。评估也可以是一个有效的工具，用于指导我们在未来改进模型。

1. 测试集

  大多数评估技术为模型计算一个得分，通过比较它在测试集（或评估集）中为输入生成的标签与那些输入的正确标签。该测试集通常与训练集具有相同的格式。然而，测试集与训练语料不同是非常重要的：如果我们简单地重复使用训练集作为测试集，那么一个只记住了它的输入而没有学会如何推广到新的例子的模型会得到误导人的高分。建立测试集时，往往是一个可用于测试的和可用于训练的数据量之间的权衡。对于有少量平衡的标签和一个多样化的测试集的分类任务，只要 100 个评估实例就可以进行有意义的评估。但是，如果一个分类任务有大量的标签或包括非常罕见的标签，那么选择的测试集的大小就要保证出现次数最少的标签至少出现 50 次。此外，如果测试集包含许多密切相关的实例——例如：来自一个单独文档中的实例——那么测试集的大小应增加，以确保这种多样性的缺乏不会扭曲评估结果。当有大量已标注数据可用时，只使用整体数据的 10％进行评估常常会在安全方面犯错。
  选择测试集时另一个需要考虑的是测试集中实例与验证集中的实例的相似程度。这两个数据集越相似，我们对将评估结果推广到其他数据集的信心就越小。

2. 准确度

  用于评估一个分类最简单的度量是准确度，测量测试集上分类器正确标注的输入的比
例。例如：一个名字性别分类器，在包含 80 个名字的测试集上预测正确的名字有 60 个，它有 60/80= 75％的准确度。nltk.classify.accuracy()函数会在给定的测试集上计算分类器模型的准确度。
  解释一个分类器的准确性得分，考虑测试集中单个类标签的频率是很重要的（也就是正反例的比值）。例如：考虑一个决定词 bank 每次出现的正确的词意的分类器。如果我们在金融新闻文本上评估分类器，那么我们可能会发现，金融机构的意思 20 个里面出现了 19 次。在这种情况下，95％的准确度也难以给人留下深刻印象，因为我们可以实现一个模型，它总是返回金融机构的意义。然而，如果我们在一个更加平衡的语料库上评估分类器，那里的最频繁的词意只占 40％，那么 95％的准确度得分将是一个更加积极的结果。

3. 精确度和召回率

  另一个准确度分数可能会产生误导的实例是在“搜索”任务中，如：信息检索，我们试图找出与特定任务有关的文档。由于不相关的文档的数量远远多于相关文档的数量，一个将每一个文档都标记为无关的模型的准确度分数将非常接近 100％。
  因此，对搜索任务使用不同的测量集是很常见的，下面的四个类别的每一个中的项目的数量：
• 真阳性（TP）是相关项目中我们正确识别为相关的。
• 真阴性（TN）是不相关项目中我们正确识别为不相关的。
• 假阳性（FP）（或 I 型错误）是不相关项目中我们错误识别为相关的。
• 假阴性（FN）（或 II型错误）是相关项目中我们错误识别为不相关的。
  给定上面四个定义，我们可以定义以下指标：

• 精确度（Precision），表示我们发现的项目中有多少是相关的，TP/(TP+ FP)。
• 召回率（Recall），表示相关的项目中我们发现了多少，TP/(TP+ FN)。
• F-度量值（F-Measure）（或 F-得分，F-Score），组合精确度和召回率为一个单独的得分，被定义为精确度和召回率的调和平均数(2 × Precision × Recall)/(Precision+Recall)。

4. 混淆矩阵

  在机器学习领域，混淆矩阵（Confusion Matrix），又称为可能性矩阵或错误矩阵。混淆矩阵是可视化工具，特别用于监督学习，在无监督学习一般叫做匹配矩阵。在图像精度评价中，主要用于比较分类结果和实际测得值，可以把分类结果的精度显示在一个混淆矩阵里面。

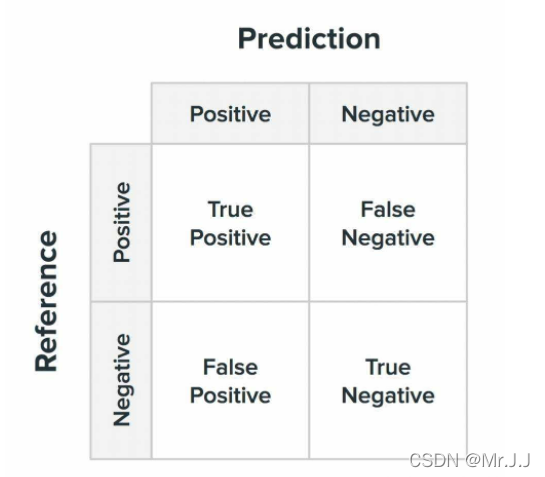
该矩阵可用于易于理解的二类分类问题，但通过向混淆矩阵添加更多行和列，可轻松应用于具有3个或更多类值的问题。
  如有150个样本数据，预测为类I，类II，类III 各为50个。分类结束后得到的混淆矩阵为：

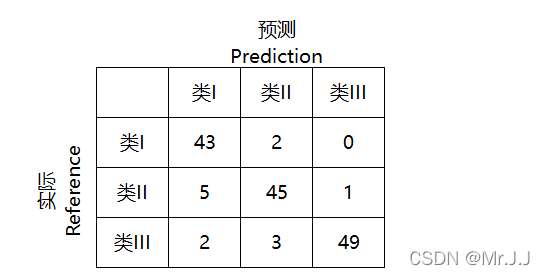
5. 交叉验证

  为了评估我们的模型，我们必须为测试集保留一部分已标注的数据。正如我们已经提到，如果测试集是太小了，我们的评价可能不准确。然而，测试集设置较大通常意味着训练集设置较小，如果已标注数据的数量有限，这样设置对性能会产生重大影响。
  这个问题的解决方案之一是在不同的测试集上执行多个评估，然后组合这些评估的得分，这种技术被称为交叉验证。特别是，我们将原始语料细分为 N 个子集称为折叠（folds）。对于每一个这些的折叠，我们使用除这个折叠中的数据外其他所有数据训练模型，然后在这个折叠上测试模型。即使个别的折叠可能是太小了而不能在其上给出准确的评价分数，综合评估得分是基于大量的数据，因此是相当可靠的。
  第二，同样重要的，采用交叉验证的优势是，它可以让我们研究不同的训练集上性能变化有多大。如果我们从所有 N 个训练集得到非常相似的分数，然后我们可以相当有信心，得分是准确的。另一方面，如果 N 个训练集上分数很大不同，那么，我们应该对评估得分的准确性持怀疑态度。

决策树

决策树
  决策树是一个简单的为输入值选择标签的流程图。这个流程图由检查特征值的决策节点和分配标签的叶节点组成。为输入值选择标签，我们以流程图的初始决策节点（称为其根节点）开始。此节点包含一个条件，检查输入值的特征之一，基于该特征的值选择一个分支。沿着这个描述我们输入值的分支，我们到达了一个新的决策节点，有一个关于输入值的特征的新的条件。我们继续沿着每个节点的条件选择的分支，直到到达叶节点，它为输入值提供了一个标签。具体流程如下图。

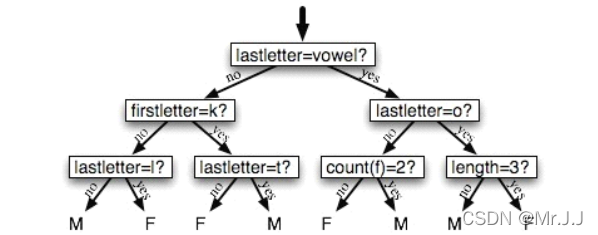
  一旦我们有了一个决策树，就可以直接用它来分配标签给新的输入值。不那么直接的是我们如何能够建立一个模拟给定的训练集的决策树。在此之前，我们看一下建立决策树的学习算法，思考一个简单的任务：为语料库选择最好的“决策树桩”。决策树桩是只有一个节点的决策树，基于一个特征决定如何为输入分类。每个可能的特征值一个叶子，为特征有那个值的输入指定类标签。要建立决策树桩，我们首先必须决定哪些特征应该使用。最简单的方法是为每个可能的特征建立一个决策树桩，看哪一个在训练数据上得到最高的准确度，也有其他的替代方案，我们将在下面讨论。一旦我们选择了一特征，就可以通过分配一个标签给每个叶子，基于在训练集中所选的例子的最频繁的标签，建立决策树桩（即选择特征具有那个值的例子）。给出了选择决策树桩的算法，生长出较大的决策树的算法就很简单了。首先，我们选择分类任务的整体最佳的决策树桩。然后，我们在训练集上检查每个叶子的准确度。没有达到足够的准确度的叶片被新的决策树桩替换，新决策树桩是在根据到叶子的路径选择的训练语料的子集上训练的。简单来说，先用哪个特征建立根节点，然后用哪个特征进行树生长，这些都会影响分类器最终的得分，所以请接着往下看。

1. 熵和信息增益

  正如之前提到的，有几种方法来为决策树桩确定最有信息量的特征。一种流行的替代方法，被称为信息增益，当我们用给定的特征分割输入值时，衡量它们变得更有序的程度。要衡量原始输入值集合如何无序，我们计算它们的标签的墒，如果输入值的标签非常不同，墒就高；如果输入值的标签都相同，墒就低。特别是，熵被定义为每个标签的概率乘以那个标签的 log 概率的总和。

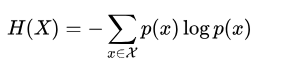
  其中x代表X可能的取值，p(x)代表其发生的概率，这里的log是指以2为底的对数。

  知道了计算公式，让我们以前面的性别例子，试着计算不同标签的熵，超级计算器。以便更好的理解公式：

1.假如标签是labels = [‘male’, ‘female’, ‘male’, ‘male’]
熵 = -(log2(0.75)*0.75+log2(0.25)*0.25)= 0.8112781244591328
2.假如标签是labels = [‘female’, ‘male’, ‘female’, ‘male’]
熵 = -(log2(0.5)*0.5+log2(0.5)*0.5)= 1

  通过上面例子你应该对计算熵有了理解，那接着编写代码计算熵。

import math 
import nltk

def entropy(labels):
    freqdist = nltk.FreqDist(labels)
    probs = [freqdist.freq(l) for l in nltk.FreqDist(labels)]
    return -sum([p * math.log(p,2) for p in probs])

# 测试
print(entropy( ['male', 'female', 'male', 'male']))
0.8112781244591328
1
2
3
4
5
6
7
8
9
10
11

  一旦我们已经计算了原始输入值的标签集的墒，就可以判断应用了决策树桩之后标签会变得多么有序。为了这样做，我们计算每个决策树桩的叶子的熵，利用这些叶子熵值的平均值（加权每片叶子的样本数量）。信息增益等于原来的熵减去这个新的减少的熵。信息增益越高，将输入值分为相关组的决策树桩就越好，于是我们可以通过选择具有最高信息增益的决策树桩来建立决策树。
  决策树的另一个考虑因素是效率。前面描述的选择决策树桩的简单算法必须为每一个可能的特征构建候选决策树桩，并且这个过程必须在构造决策树的每个节点上不断重复。已经开发了一些算法通过存储和重用先前评估的例子的信息减少训练时间。

2. 信息增益比

  为了改善单纯的信息增益算法的缺陷，引入了信息增益比。其计算逻辑如下，但我感觉不容易理解，理解这些计算逻辑，还是西瓜书讲解的清晰，各位有需要的可以去自行搜索研读。

3. 基尼系数

  采用信息增益比可以改善部分不足，但还会有缺陷，进而又有了基尼系数的概念，其计算如下：

4. 优缺点

  说了这么多，其实每个概念对应一种树算法，ID3算法对应信息增益，C4.5决策树对应信息增益比，cart决策树对应基尼系数。虽然在不断的优化，但决策树还是存在一些目前无法结局的缺陷，下面看看决策树的优缺点。
决策树的优势：

• 便于理解和解释。树的结构可视化。
• 训练需要的数据少，其他机器学习模型通常需要数据规范化，比如构建虚拟变量和移除缺失值
• 能够处理数值型数据和分类数据，其他的技术通常只能用来专门分析某一种的变量类型的数据集（但更倾向于分类）
• 使用白盒模型。如果某种给定的情况在模型中是可以观察的，那么就可以轻易的通过布尔逻辑来解释这种情况，相比之下在黑盒模型中的结果就是很难说明清楚了；
• 可以通过数值统计测试来验证该模型。这对解释验证该模型的可靠性成为可能
• 即使是该模型假设的结果越真实模型所提供的数据有些违反，其表现依旧良好

决策树的缺点：

• 决策树模型容易产生一个过于复杂的模型，也就是过拟合，所以有各种剪枝策略（预剪枝和后剪枝）
• 决策树可能是不稳定的，数据中的微小变化可能会导致完全不同的树生成（树集成可解决）
• 决策树对数据有要求，即正反比例要相对平衡
• 由于其算法的逻辑，其对分支更多的特征越友好

朴素贝叶斯分类器

  在朴素贝叶斯分类器中，每个特征都得到发言权，来确定哪个标签应该被分配到一个给定的输入值。为一个输入值选择标签，朴素贝叶斯分类器以计算每个标签的先验概率开始，它由在训练集上检查每个标签的频率来确定。之后，每个特征的贡献与它的先验概率组合，得到每个标签的似然估计。似然估计最高的标签会分配给输入值。

1、朴素贝叶斯分类器

  关于朴素贝叶斯分类器，我的理解和认识如下：


推导过程：

  了解了理论基础后，借用西瓜书的例子，代入式学习上面的理论。首先数据集如图1，最后需要预测的为图2，过程如图3：
图1：

图2：
图3：

  由于 0.038 > 6.80 x 10^-5,因此 朴素贝叶斯分类器将测试样本"测 1" 判别为"好瓜"。也就是说，在已知的条件下（图2中的各种特征），该瓜是好瓜的概率远大于坏瓜，所以预测为好瓜。

  这里要说下各种条件概率计算的逻辑：

  需注意，若某个属性值在训练集中没有与某个类同时出现过，则直接基于上面的步骤进行概率估计就会出现以下情况：

  所以上面的连乘式计算出的概率值为零，因此，无论该样本的其他属性是什么，哪怕在其他属性上明显像好瓜，分类的结果都将是"好瓜=否"这显然太合理理.。为了避免其他属性携带的信息被训练集中未出现的属性值"抹去’，在估计概率值时通常要进行"平滑" (smoothing) ，常用"拉普拉斯修正" (Laplacian correctio ）

2、拉普拉斯平滑

  法国数学家 拉普拉斯 最早提出用 加1 的方法，估计没有出现过的现象的概率。则上面例子中的条件概率计算变成如下，其中N表示训练集中可能的类别数。