（5-2）Floyd算法：Floyd算法的核心思想

Floyd算法是一种用于解决图中所有节点对之间的最短路径问题的经典算法，它通过动态规划的思想，逐步更新节点对之间的最短路径长度。

5.2.1  Floyd算法的原理和实现步骤

Floyd算法的核心思想是利用动态规划，逐步更新节点对之间的最短路径长度。具体而言，Floyd算法通过考虑所有节点作为中间节点的可能性，尝试通过中间节点来改进节点对之间的最短路径。

Floyd算法的实现步骤如下所示。

（1）初始化：将每对节点之间的距离初始化为它们之间的直接距离，如果直接连接不存在，则设置为无穷大。同时，初始化一个大小为n的二维数组dist，其中dist[i][j]表示从节点i到节点j的最短路径长度。

（2）逐步更新：对于每一对节点i和j，尝试通过中间节点k来更新i到j的最短路径长度。具体地，遍历所有节点k，如果从节点i到节点k再到节点j的路径长度小于直接连接i到j的路径长度，则更新dist[i][j]为更短的路径长度。

（3）重复更新：重复进行上述步骤，直到所有节点对之间的最短路径长度不再改变为止。

（4）输出结果：得到更新后的节点对之间的最短路径长度，以及路径上的中间节点。

例如下面是一个简单的C++例子，演示了Floyd算法的实现过程。

void floydWarshall(int graph[][V]) {
    int dist[V][V];
 
    // Initialize the distance matrix
    for (int i = 0; i < V; i++)
        for (int j = 0; j < V; j++)
            dist[i][j] = graph[i][j];
 
    // Update distance matrix using all vertices as intermediate nodes
    for (int k = 0; k < V; k++) {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j])
                    dist[i][j] = dist[i][k] + dist[k][j];
            }
        }
    }
 
    // Print the shortest distances
    // ...
}

在上述代码中，graph表示图的邻接矩阵，V表示节点的数量，INF表示正无穷大。floydWarshall函数用于计算所有节点对之间的最短路径长度，最终更新到dist矩阵中。

5.2.2  Floyd算法的计算过程

问题的提出：已知一个各边权值均大于0的带权有向图，对每一对顶点 vi ¹ vj，要求求出vi 与vj之间的最短路径和最短路径长度。

Floyd算法求最短路径步骤如下：

1. 初始时设置一个n阶方阵，令其对角线元素为0，若存在弧<Vi,Vj>，则对应元素为权值；否则为µ。
2. 逐步试着在原直接路径中增加中间顶点，若加入中间点后路径变短，则修改之；否则，维持原值。
3. 所有顶点试探完毕，算法结束。

从图的带权邻接矩阵G.arcs出发，假设求顶点vj到vj的最短路径。如果从vi到vj有弧，则从Vi到Vj存在一条长度为G.arcs[i][j]的路径，但该路径是否一定是最短路径，还需要进行n次试探，具体说明如下所示。

1. 判别（Vi, V0）和（ V0，Vj），即判别(Vi, V0 , Vj）是否存在，若存在，则比较（ Vi, Vj ）和(Vi, V0 , Vj）的长度，取长度较短的为从Vi到Vj的中间顶点序号不大于0的最短路径。
2. 再加一个顶点V1，如果(Vi, … , V1） 和(V1, … , Vj）分别是当前找到的中间顶点序号不大于0的最短路径，那么(Vi, … , V1, … , Vj ）就有可能是从Vi到Vj的中间顶点序号不大于1的最短路径。将它和已经得到的从Vi到Vj之间顶点序号不大于0的最短路径相比较，取较短者为从Vi到Vj的中间顶点序号不大于1的最短路径。
3. 再加一个顶点V2，继续进行试探。

请看下面的图5-1，D(-1)为有向网的邻接矩阵

第1步：以D(-1)为基础，以V0为中间顶点，求从Vi到Vj的最短路径。该路径或者为从Vi到Vj的边, 或者为(Vi,V0)+(V0,Vj) 。

D(0) [i][j] = min{D(-1) [i][j], D(-1) [i][0]+D(-1) [0][j]}

min{D(-1) [i][j], D(-1) [i][0]+D(-1) [0][j]}

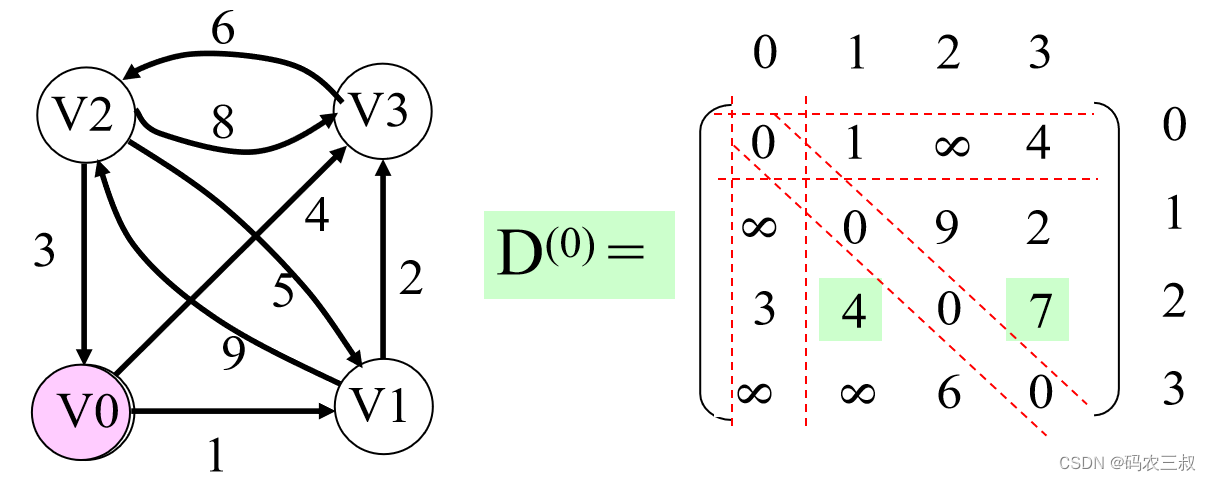
图5-1  有向网的邻接矩阵D(-1)

第2步：接下来以D(0)为基础，以V1为中间顶点，求从Vi,到Vj的最短路径，如图5-2所示。该路径或者为从Vi到Vj的边, 或者为从Vi开始通过V0或V1到达Vj的最短路径 。

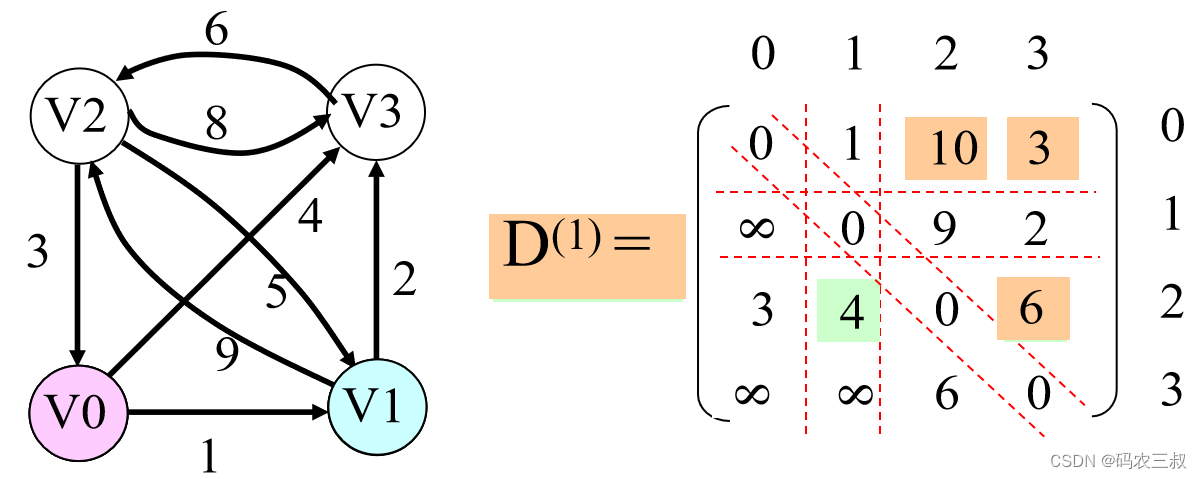
图5-2  以D(0)为基础，以V1为中间顶点

D(1) [i][j] = min{D(0) [i][j], D(0) [i][1]+D(0) [1][j]}

第3步：接下来以D(1)为基础，以V2为中间顶点，求从Vi,到Vj的最短路径，如图5-3所示。或者为从Vi到Vj的边, 或者为从Vi开始通过V0,V1, V2到达Vj的最短路径。

D(2) [i][j] =min{D(1) [i][j], D(1) [i][2]+D(1) [2][j]}

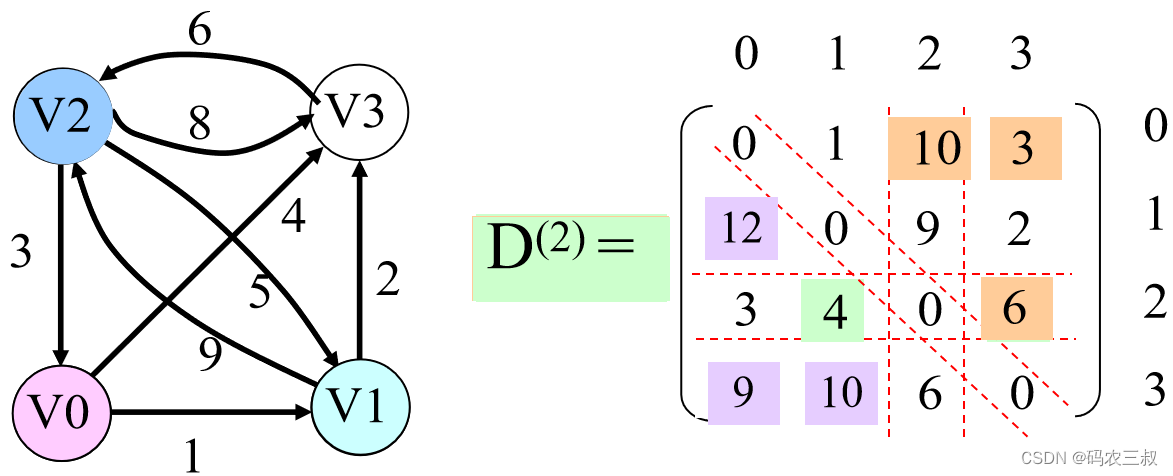
图5-3  以D(1)为基础，以V2为中间顶点

第4步：以D(2)为基础，以V3为中间顶点，求从Vi,到Vj的最短路径，如图5-4所示。或者为从Vi到Vj的边, 或者为从Vi开始通过V0,V1, V2,V3到达Vj的最短路径。

D(3) [i][j] = min{D(2) [i][j], D(2) [i][3]+D(2) [3][j]}

D(3) [i][j] 即为从Vi到Vj的最短路径长度。

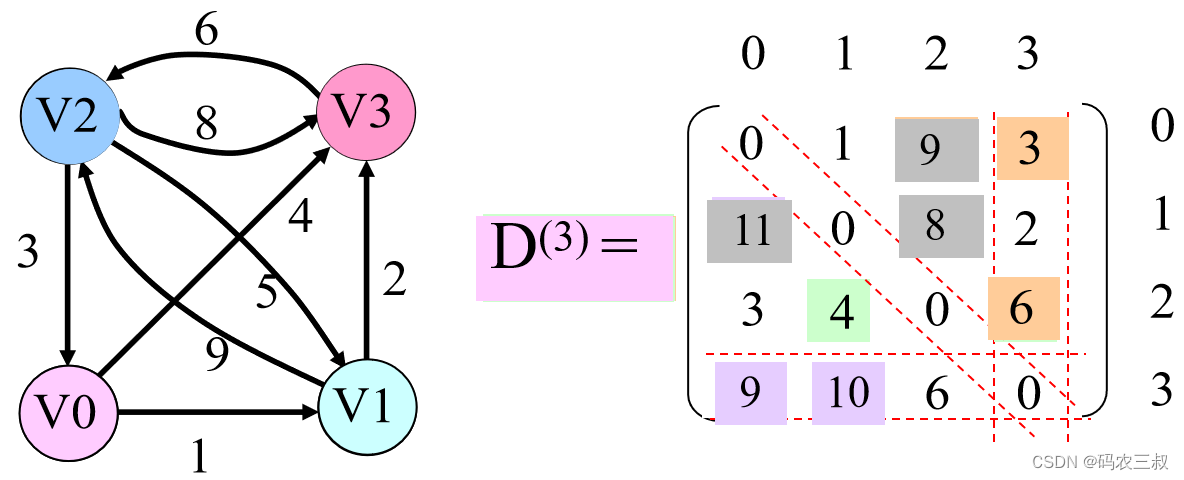
图5-4  以D(2)为基础，以V3为中间顶点

请看下面的例子，使用Floyd算法计算了给定图中所有节点对之间的最短路径，并将计算结果可视化展示出来。

实例5-1：使用Floyd算法计算了给定图中所有节点对之间的最短路径（codes/5/Floyd/Floyd.cpp）

实例文件Floyd.cpp的具体实现代码如下所示。

#include <opencv2/opencv.hpp>
#include <iostream>
#include <vector>
 
using namespace std;
using namespace cv;
 
// 输出最短路径并绘制在图中
void printShortestPath(vector<vector<int>>& graph, vector<vector<int>>& next, int start, int end) {
    cout << "从节点 " << start << " 到节点 " << end << " 的最短路径为：";
    cout << start << " ";
    while (start != end) {
        start = next[start][end];
        cout << start << " ";
    }
    cout << endl;
}
 
// Floyd算法
void floydAlgorithm(vector<vector<int>>& graph, Mat& result) {
    int V = graph.size();
 
    // 初始化结果矩阵
    result = Mat::zeros(V, V, CV_8UC1);
 
    // 初始化下一个节点矩阵
    vector<vector<int>> next(V, vector<int>(V, -1));
    for (int i = 0; i < V; ++i) {
        for (int j = 0; j < V; ++j) {
            if (graph[i][j] != INT_MAX && i != j) {
                next[i][j] = j;
            }
        }
    }
 
    // Floyd算法
    for (int k = 0; k < V; k++) {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                if (graph[i][k] != INT_MAX && graph[k][j] != INT_MAX &&
                    graph[i][k] + graph[k][j] < graph[i][j]) {
                    graph[i][j] = graph[i][k] + graph[k][j];
                    next[i][j] = next[i][k];
                    result.at<uchar>(i, j) = 255; // 设置白色像素以表示最短路径
                }
            }
        }
    }
 
    // 输出最短路径
    for (int i = 0; i < V; ++i) {
        for (int j = 0; j < V; ++j) {
            if (i != j && next[i][j] != -1) {
                printShortestPath(graph, next, i, j);
            }
        }
    }
}
 
int main() {
    // 生成随机图（邻接矩阵）
    int V = 5; // 节点数
    vector<vector<int>> graph(V, vector<int>(V, INT_MAX)); // 初始化为最大整数值
 
    // 设置一些随机路径
    graph[0][1] = 1;
    graph[1][0] = 1;
    graph[0][2] = 3;
    graph[2][0] = 3;
    graph[1][2] = 2;
    graph[2][1] = 2;
    graph[1][3] = 2;
    graph[3][1] = 2;
    graph[2][4] = 1;
    graph[4][2] = 1;
    graph[3][4] = 3;
    graph[4][3] = 3;
 
    // 应用Floyd算法
    Mat result;
    floydAlgorithm(graph, result);
 
    // 显示结果
    namedWindow("Shortest Paths", WINDOW_NORMAL);
    resizeWindow("Shortest Paths", 400, 400);
 
    // 绘制节点名
    int fontFace = FONT_HERSHEY_SIMPLEX;
    double fontScale = 0.5;
    int thickness = 1;
    for (int i = 0; i < V; ++i) {
        string text = to_string(i);
        Point textOrg(20 * i, 20 * i);
        putText(result, text, textOrg, fontFace, fontScale, Scalar::all(255), thickness, LINE_AA);
    }
 
    imshow("Shortest Paths", result);
    waitKey(0);
 
    return 0;
}

上述代码的实现流程如下所示：

（1）首先，定义了一个函数printShortestPath，用于打印输出最短路径。

（2）其次，实现了Floyd算法，该算法用于计算给定图的所有节点对之间的最短路径。具体而言，该算法会生成一个邻接矩阵来表示图的连接关系，并进行迭代计算，更新矩阵中的值以找到最短路径。

（3）接着，使用库OpenCV绘制可视化结果，以便更直观地了解图的结构。

（4）最后，显示了生成的图像，将最短路径和节点名以图形方式展现出来，使用户能够清晰地看到图的结构和最短路径信息。

执行后会打印输出计算的最短路径：

从节点 0 到节点 1 的最短路径为：0 1
从节点 0 到节点 2 的最短路径为：0 2
从节点 0 到节点 3 的最短路径为：0 1 3
从节点 0 到节点 4 的最短路径为：0 2 4
从节点 1 到节点 0 的最短路径为：1 0
从节点 1 到节点 2 的最短路径为：1 2
从节点 1 到节点 3 的最短路径为：1 3
从节点 1 到节点 4 的最短路径为：1 2 4
从节点 2 到节点 0 的最短路径为：2 0
从节点 2 到节点 1 的最短路径为：2 1
从节点 2 到节点 3 的最短路径为：2 1 3
从节点 2 到节点 4 的最短路径为：2 4
从节点 3 到节点 0 的最短路径为：3 1 0
从节点 3 到节点 1 的最短路径为：3 1
从节点 3 到节点 2 的最短路径为：3 1 2
从节点 3 到节点 4 的最短路径为：3 4
从节点 4 到节点 0 的最短路径为：4 2 0
从节点 4 到节点 1 的最短路径为：4 2 1
从节点 4 到节点 2 的最短路径为：4 2
从节点 4 到节点 3 的最短路径为：4 3

绘制的可视化图如图5-4所示。

图5-4  绘制的可视化图

未完待续