机器学习---迁移学习方法_迁移学习基础算法框架

1. 问题形式化

迁移学习的问题形式化，是进行一切研究的前提。在迁移学习中，有两个基本的概念：领域

(Domain) 和任务 (Task)。它们是最基础的概念。

1.1 领域

领域 (Domain): 是进行学习的主体。领域主要由两部分构成：数据和生成这些数据的概率分布。通

常我们用 D 来表示一个 domain，用大写 P 来表示一个概率分布。特别地，因为涉及到迁移，所以

对应于两个基本的领域：源领域 (Source Domain) 和目标领域 (Target Domain)。这两个概念很好

理解。源领域就是有知识、有大量数据标注的领域，是我们要迁移的对象；目标领域就是我们最终

要赋予知识、赋予标注的对象。知识从源领域传递到目标领域，就完成了迁移。

领域上的数据，我们通常用小写粗体 x 来表示，它也是向量的表示形式。例如，xi 就表示第 i 个样

本或特征。用大写的黑体 X 表示一个领域的数据，这是一种矩阵形式。我们用大写花体 X 来表示

数据的特征空间。通常我们用小写下标 s 和 t 来分别指代两个领域。结合领域的表示方式，则：Ds

表示源领域，Dt 表示目标领域。值得注意的是，概率分布 P 通常只是一个逻辑上的概念，即我们

认为不同领域有不同的概率分布，却一般不给出（也难以给出）P 的具体形式。

1.2 任务

任务 (Task): 是学习的目标。任务主要由两部分组成：标签和标签对应的函数。通常我们用花体 Y

来表示一个标签空间，用 f(·) 来表示一个学习函数。相应地，源领域和目标领域的类别空间就可以

分别表示为 Ys 和 Yt 。我们用小写 ys 和yt 分别表示源领域和目标领域的实际类别。

1.3 常用符号总结

迁移学习（Transfer Learning）：给定一个有标记的源域和一个无 标记的目标域

。这两个领域的数据分布P（xs）和P（x1）不同，即P（xs）≠P（xt）。迁移学

习的目的就是要借助Ds的知识，来学习目标域Dt的知识（标签）。更进一步，结合我们前面说过

的迁移学习研究领域，迁移学习的定义需要进行如下的考虑：

（1）特征空间的异同，即Xs和Xt是否相等。

（2）类别空间的异同：即ys和yt是否相等。

（3）条件概率分布的异同：即Qs（ys｜xs）和Qt（yt | xt）是否相等。

结合上述形式化，我们给出领域自适应（Domain Adaptation）这一热门研究方向的定义：

领域自适应（Domain Adaptation）：给定一个有标记的源域和一个 无标记的目标

域，假定它们的特征空间相同，即Xs＝Xt，并且它们的类别空间也相同，即ys＝yt

以及条件概率分布也相同，即Qs（ys｜xs）＝Qt（yt｜xt）。但是这两个域的边缘分布不同，即Ps

（xs）≠Pt（xt）。迁移学习的目标就是，利用有标记的数据Ds去学习一个分类器f：xt→yt来预测

目标域Dt的标签。

迁移学习的核心是，找到源领域和目标领域之间的相似性，并加以合理利用。这种相似性非常普

遍。比如，不同人的身体构造是相似的；自行车和摩托车的骑行方式是相似的；国际象棋和中国象

棋是相似的；羽毛球和网球的打球方式是相似的。这种相似性也可以理解为不变量。以不变应万

变，才能立于不败之地。 找到相似性 (不变量)，是进行迁移学习的核心。有了这种相似性后，下

一步工作就是，如何度量和利用这种相似性。度量工作的目标有两点：一是很好地度量两个领域的

相似性，不仅定性地告诉我们它们是否相似，更定量地给出相似程度。二是以度量为准则，通过我

们所要采用的学习手段，增大两个领域之间的相似性，从而完成迁移学习。

1.4 度量

定义在两个向量 (两个点) 上，这两个数据在同一个分布里。点 x 和点 y 的马氏距离为：

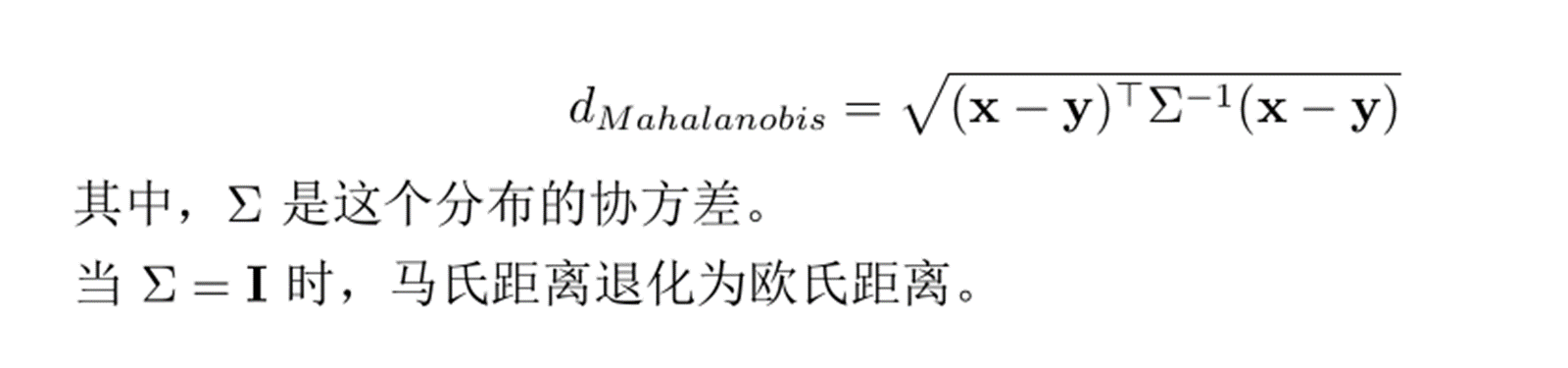
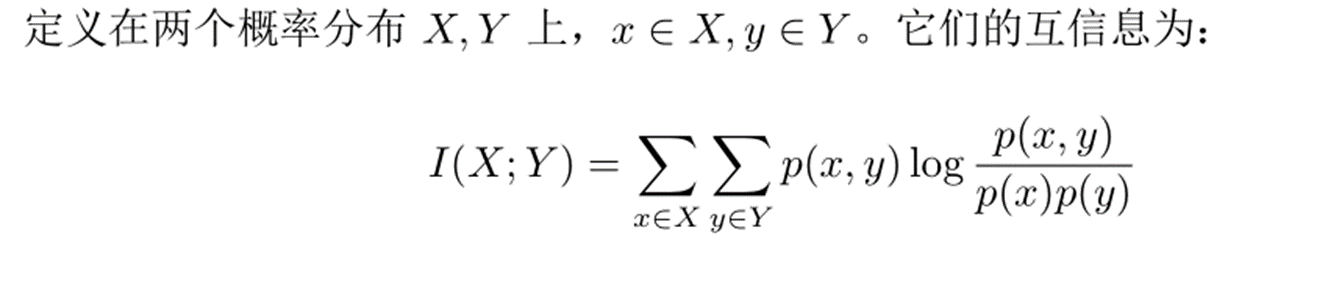
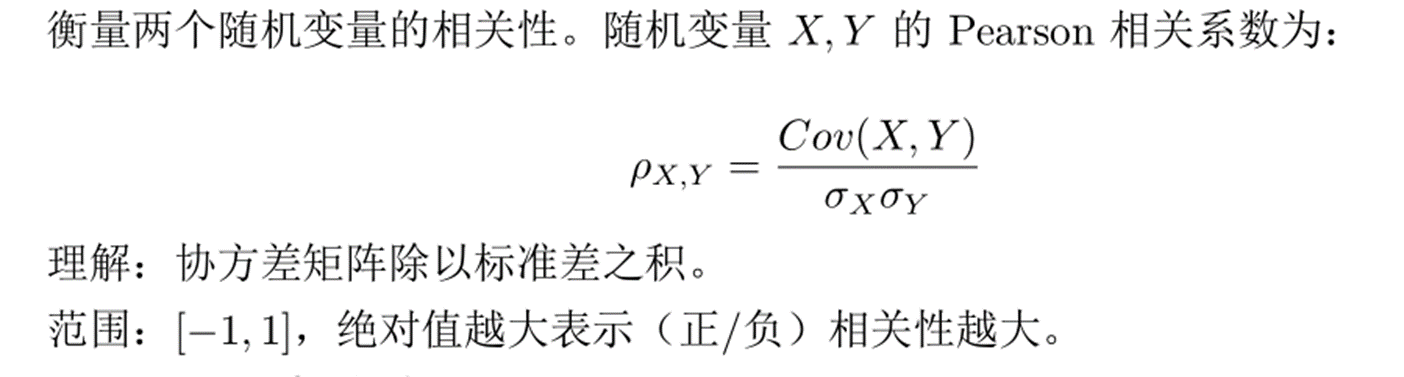
最大均值差异是迁移学习中使用频率最高的度量。Maximum mean discrepancy，它度量在再生希

尔伯特空间中两个分布的距离，是一种核学习方法。两个随机变量的 MMD 平方距离为：

其中φ（`）是映射，用于把原变量映射到再生核希尔伯特空间中。什么是RKHS？形式化定义太复

杂， 简单来说希尔伯特空间是对于函数的内积完备的，而再生核希尔伯特空间是具有再生性

的希尔伯特空间。就是比欧几里得空间更高端的。将平方展开

后，RKHS空间中的内积就可以转换成核函数，所以最终MMD可以直接通过核函数进行计算。

2. 迁移学习的基本方法

2.1 基于样本迁移

基于样本的迁移学习方法 (Instance based Transfer Learning) 根据一定的权重生成规则，对数据样

本进行重用，来进行迁移学习。图片形象地表示了基于样本迁移方法的思想。源域中存在不同种类

的动物，如狗、鸟、猫等，目标域只有狗这一种类别。在迁移时，为了最大限度地和目标域相似，

我们可以人为地提高源域中属于狗这个类别的样本权重。

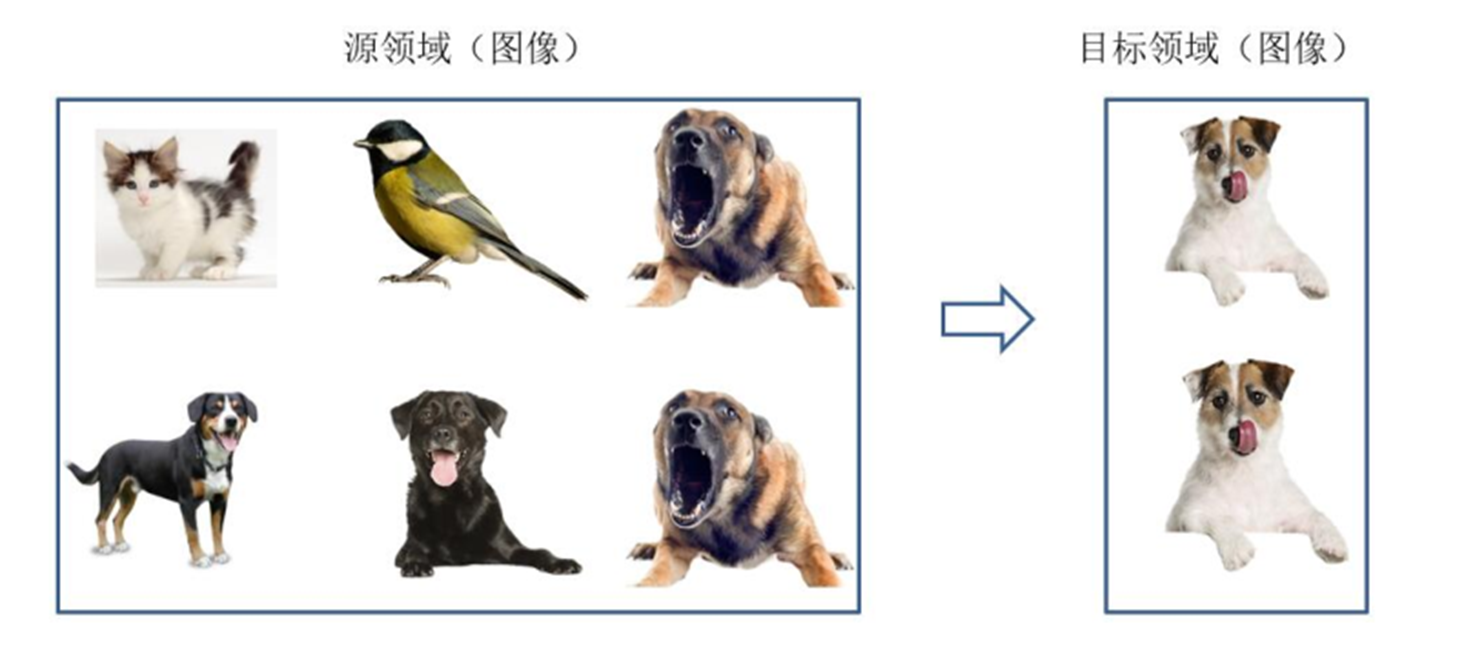
虽然实例权重法具有较好的理论支撑、容易推导泛化误差上界，但这类方法通常只在领域间分布差

异较小时有效，因此对自然语言处理、计算机视觉等任务效果并不理想。 

2.2 基于特征迁移

基于特征的迁移方法 (Feature based Transfer Learning) 是指将通过特征变换的方式互相迁移 ，来

减少源域和目标域之间的差距；或者将源域和目标域的数据特征变换到统一特征空间中，然后利用

传统的机器学习方法进行分类识别。根据特征的同构和异构性，又可以分为同构和异构迁移学习。

图片很形象地表示了两种基于特征的迁移学习方法。 

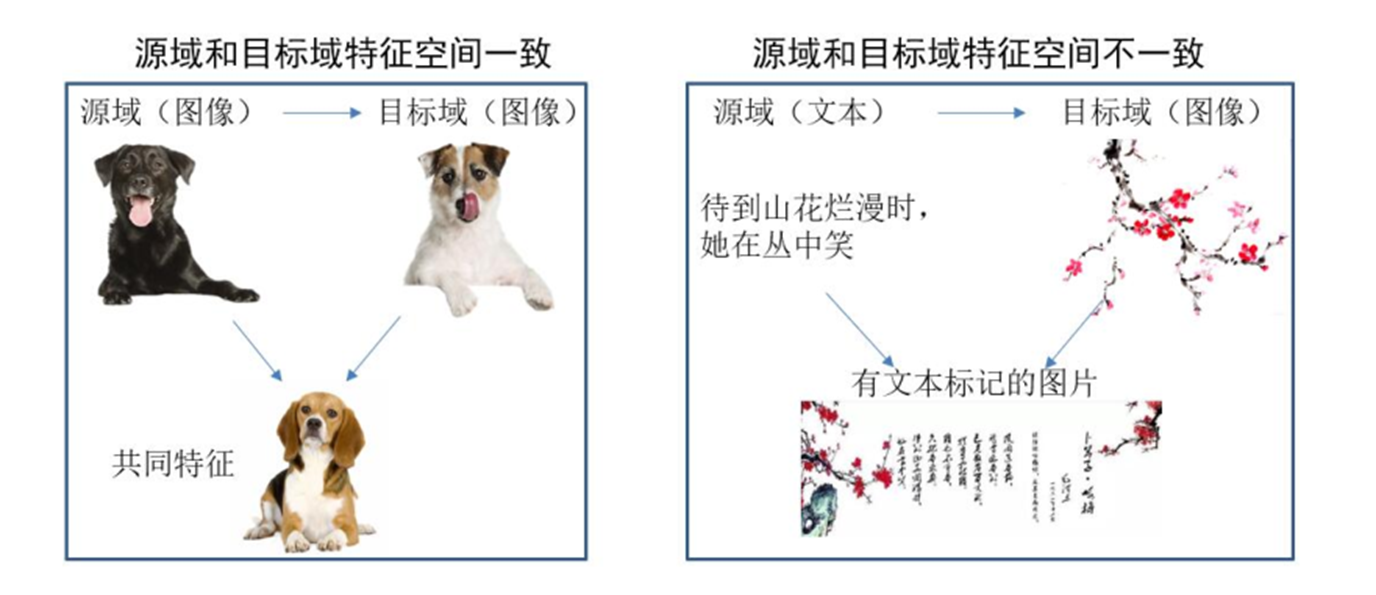
基于特征的迁移学习方法是迁移学习领域中最热门的研究方法，这类方法通常假设源域和目标域间

有一些交叉的特征。 

2.3 基于模型迁移

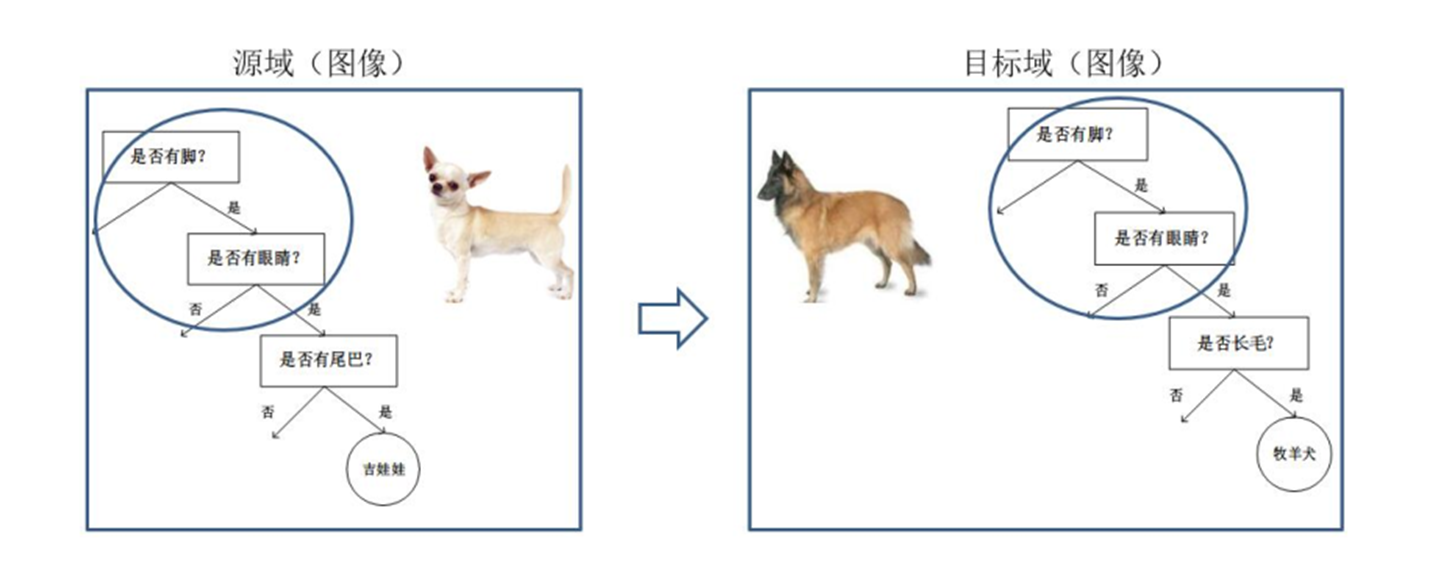
基于模型的迁移方法 (Parameter/Model based Transfer Learning) 是指从源域和目标域中找到他们

之间共享的参数信息，以实现迁移的方法。这种迁移方式要求的假设条件是：源域中的数据与目标

域中的数据可以共享一些模型的参数。

2.4 基于关系迁移 

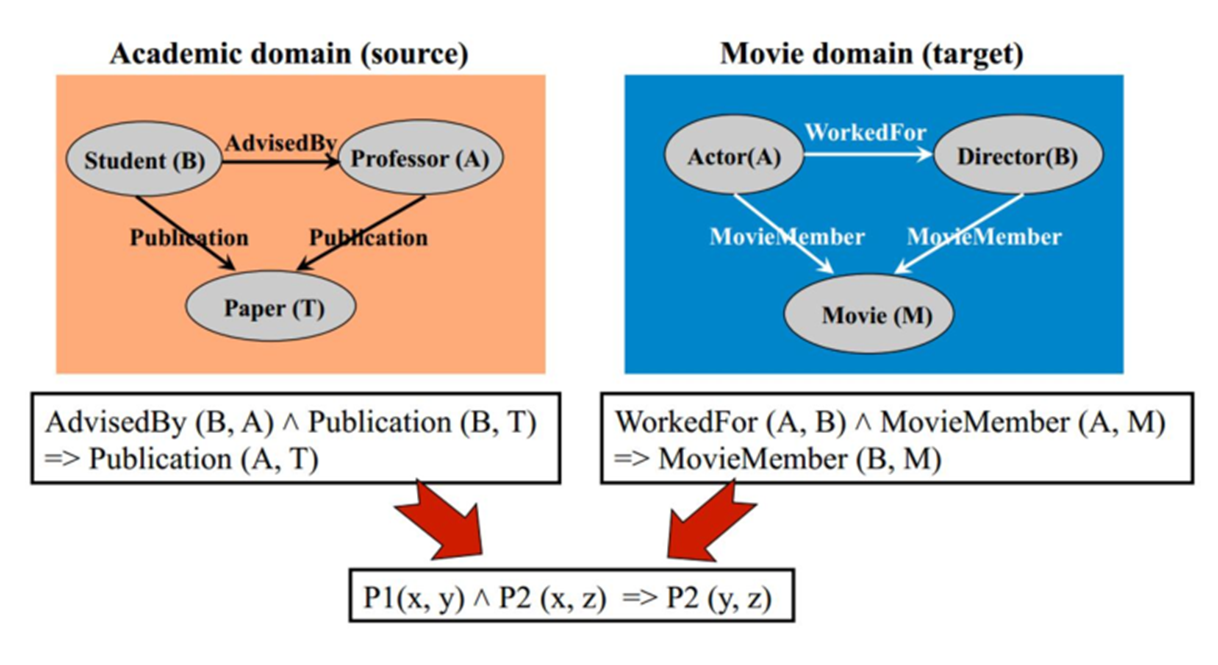
基于关系的迁移学习方法 (Relation Based Transfer Learning) 与上述三种方法具有截然不同的思

路。这种方法比较关注源域和目标域的样本之间的关系。图片形象地表示了不同领域之间相似的关

系。就目前来说，基于关系的迁移学习方法的相关研究工作非常少，大部分都借助于马尔科夫逻辑

网络 (Markov Logic Net) 来挖掘不同领域之间的关系相似性。

2.5 基于马尔科夫逻辑网的关系迁移 

3. 迁移学习算法-TCA 

3.1 数据分布自适应 

数据分布自适应 (Distribution Adaptation) 是一类最常用的迁移学习方法。这种方法的基本思想

是，由于源域和目标域的数据概率分布不同，那么最直接的方式就是通过一些变换，将不同的数据

分布的距离拉近。根据数据分布的性质，这类方法又可以分为边缘分布自适应、条件分布自适应、

以及联合分布自适应。

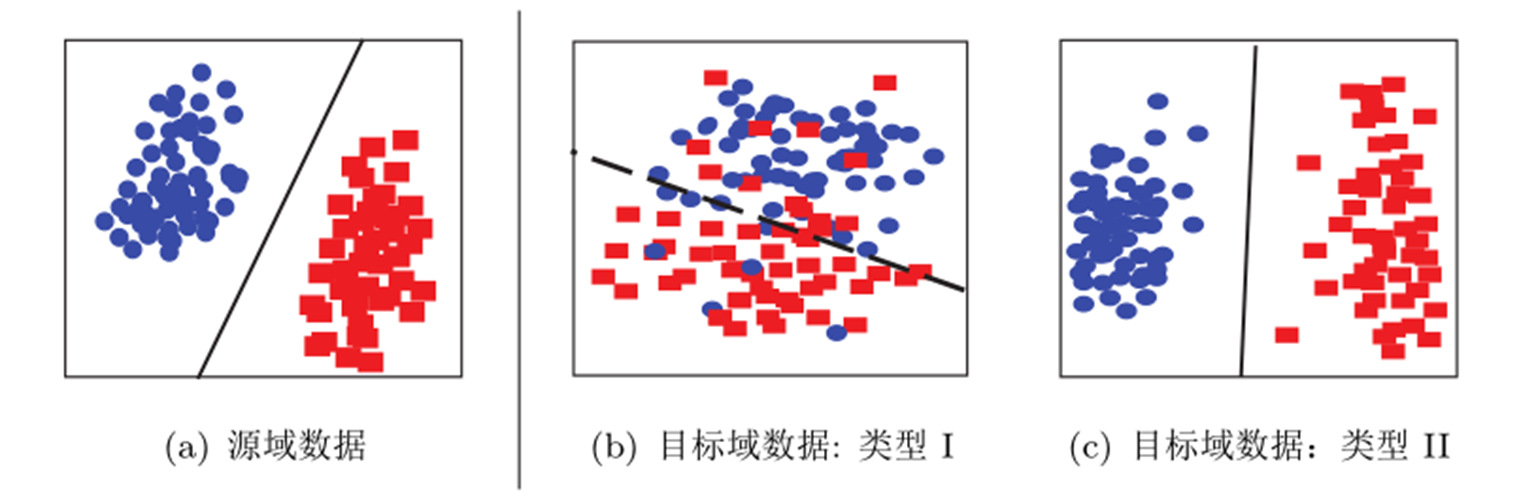
图片形象地表示了几种数据分布的情况。简单来说，数据的边缘分布不同，就是数据整体不相似。

数据的条件分布不同，就是数据整体相似，但是具体到每个类里，都不太相似。

3.2 TCA 

迁移成分分析 (Transfer Component Analysis)是一种边缘分布自适应方法 (Marginal Distribution

Adaptation) 。其目标是减小源域和目标域的边缘概率分布的距离，从而完成迁移学习。从形式上

来说，边缘分布自适应方法是用 P(xs )和 P(xt ) 之间的距离来近似两个领域之间的差异。即：

边缘分布自适应的方法最早由香港科技大学杨强教授团队提出。

边缘分布自适应的方法最早由香港科技大学杨强教授团队提出，方法名称为迁移成分分析(Transfer

Component Analysis)。由于P(xs)≠P(xt),因此，直接减小二者之间的距离是不可行的。TCA假设存

在一个特征映射Φ，使得映射后数据的分布。TCA假设如果边缘分布接近，

那么两个领域的条件分布也会接近，即条件分布。这就是TCA的全

部思想。因此，我们现在的目标是，找到这个合适的Φ。

问题：但是世界上有无穷个这样的Φ，我们肯定不能通过穷举的方法来找 Φ 的。那么怎么办

呢？ 迁移学习的本质：最小化源域和目标域的距离。能否先假设这个Φ是已知的，然后去求距离，

看看能推出什么？

更进一步，这个距离怎么算？机器学习中有很多种形式的距离，从欧氏距离到马氏距离，从曼哈顿

距离到余弦相似度，我们需要什么距离呢？TCA利用了一个经典的也算是比较“高端”的距离叫做最

大均值差异(MMD,maximum mean discrepancy)。我们令n1,n2分别表示源域和目标域的样本个

数，那么它们之间的MMD距离可以计算为：

MMD是做了一件什么事呢？简单，就是求映射后源域和目标域的均值之差。

事情到这里似乎也没什么进展：我们想求的Φ仍然没法求。TCA是怎么做的呢，这里就要感谢矩阵

了！我们发现，上面这个MMD距离平方展开后，有二次项乘积的部分！那么，联系在SVM中学过

的核函数，把一个难求的映射以核函数的形式来求，不就可以了？于是，TCA引入了一个核矩阵

K：以及一个MMD矩阵L，它的每个元素的计算方式为：

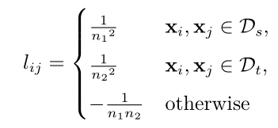
这样的好处是，直接把那个难求的距离，变换成了下面的形式：

其中，tr(`)操作表示求矩阵的迹，用人话来说就是一个矩阵对角线元素的和。这样是不是感觉离目

标又进了一步呢？ 

其实这个问题到这里就已经是可解的了，也就是说，属于计算机的部分已经做完了。只不过它是一

个数学中的半定规划(SDP,semi-definite programming)的问题，解决起来非常耗费时间。由于TCA

的第一作者Sinno Jialin Pan以前是中山大学的数学硕士，他想用更简单的方法来解决。他是怎么

做的呢？他想出了用降维的方法去构造结果。用一个更低维度的矩阵W：

这里的W矩阵是比K更低维度的矩阵。最后的W就是

问题的解答了！

好了，问题到这里，整理一下，TCA最后的优化目标是：

这里的H是一个中心矩阵，。

以上式子下面的条件是什么意思呢？那个 min 的目标就是要最小化源域和目标域的距离，加上 W

的约束让它不能太复杂。下面的条件是是要实现第二个目标：维持各自的数据特征。TCA 要维持

的特征是scatter matrix，就是数据的散度。就是说，一个矩阵散度怎么计算？对于一个矩阵 A，它

的 scatter matrix 就是AHA⊤ 。这个 H 就是上面的中心矩阵。

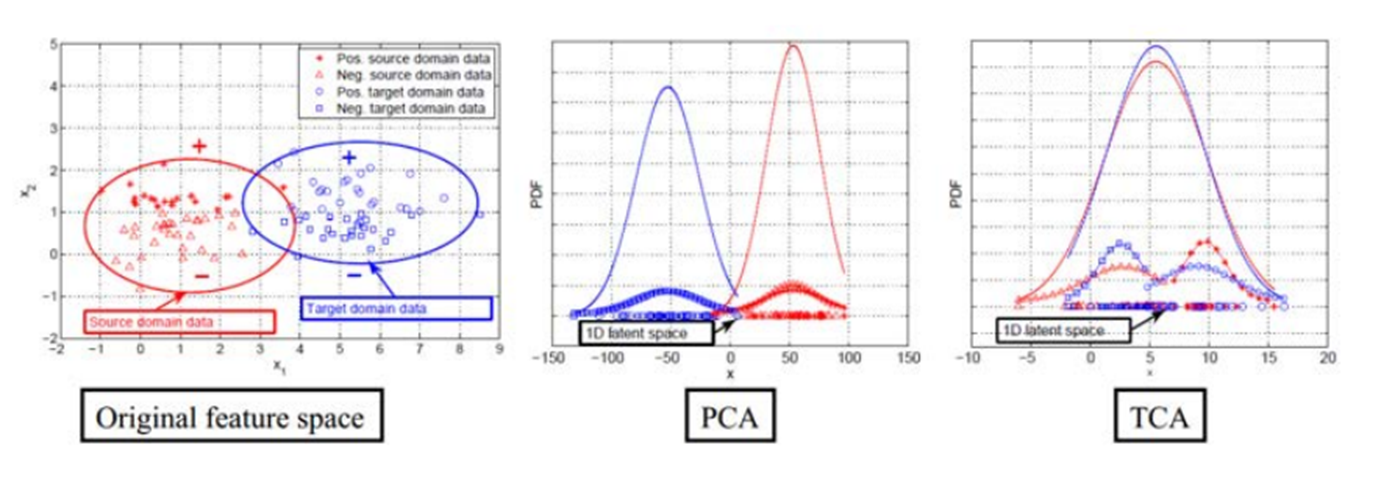
3.3 TCA 和 PCA 的效果对比

可以很明显地看出，对于概率分布不同的两部分数据，在经过 TCA处理后，概率分布更加接近。

这说明了 TCA 在拉近数据分布距离上的优势。