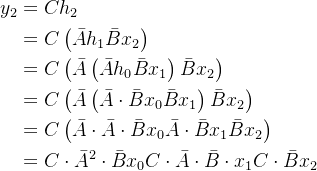- 1数据恢复与硬盘修理_pc3000 isa工具软件的组成
- 2Ubuntu系统下安装和配置Zabbix_ubuntu安装zabbix
- 319-ESP32-S3外设IIC_esp32s3 i2c
- 4当大语言模型遇到AI绘画-google gemma与stable diffusion webui融合方法-矿卡40hx的AI一体机_gemma webui
- 5def __init__(self)和def __init__(self, 参数1,参数2,···,参数n)的用法详解_definitself
- 6Flutter项目安装、调试常见问题_build service could not create build operation: un
- 7随笔-关系抽取(三) — Dependency-based Models_dependency based search
- 8word2vec使用指导_spssau使用word2vec
- 9【Rust】——项目实例:——命令行实例(一)_rust 项目例子
- 10论文总结 -论文写作注意事项(持续更)_论文的significance写些什么
【转载】解读Mamba序列模型_mamba模型
赞
踩
目录
1. SSM的起源:从Transformer复杂度、RNN到SSM
1.3.2 什么是状态空间模型SSM——RNN本质就是一个SSM
2.1 SSM到S4的三步升级:离散化SSM、循环/卷积表示、基于HiPPO处理长序列
2.1.1 离散数据的连续化:基于零阶保持技术做连续化并采样
2.2(选读) Mamba一作Albert Gu举的S4的一个应用示例
2.2.1 改进transformer不擅长处理超长的序列的问题:输入u到状态x
2.2.2 HiPPO的定义与推导:state compresses the history of input
2.3 SSM的问题:矩阵不随输入不同而变化,无法针对输入做针对性推理
2.3.1 Linear Time Invariance规定 SSM中的A、B、C不因输入不同而不同
2.3.2 如何改进S4以根据各个token重要性程度的不同而选择性聚焦的示例
3.1 Mamba = 有选择处理信息 + 硬件感知算法 + 更简单的SSM架构
3.1.1.1 mamba前身S4的4个参数的不随输入不同而不同
3.1.2 硬件感知的设计:并行扫描(parallel scan)且借鉴Flash Attention
3.2.2 三个任务的对比:coping、selective copying、induction heads
原文链接:一文通透想颠覆Transformer的Mamba:从SSM、HiPPO、S4到Mamba
1. SSM的起源:从Transformer复杂度、RNN到SSM
1.1 Transformer的二次复杂度
在transformer中,计算复杂度和序列长度的平方
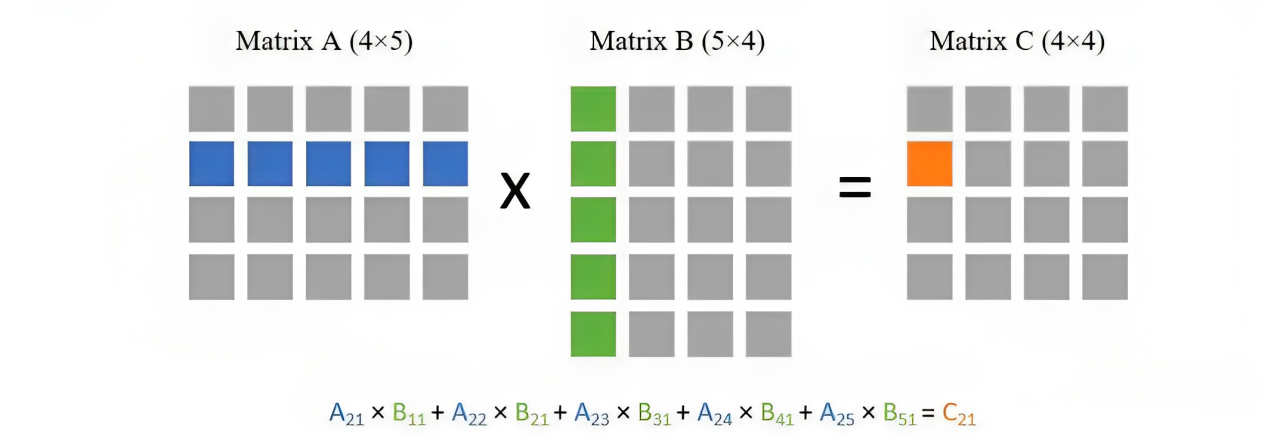
成正比,可以看一个小例子,比如两个相乘的矩阵大小分别为(
) 和(
),矩阵乘法的一种计算方式是使用第一个矩阵的每一行与第二个矩阵的每一列做点乘:
因为我们需要拿第一个矩阵的每一行去与第二个矩阵的每一列做点乘,所以总共就需要
次点乘。而每次点乘又需要
次乘法,所以总复杂度就为
精确理解的话,当输入批次大小为
,序列长度为
时,
层transformer模型的计算量为
,
则代表词向量的维度或者隐藏层的维度(隐藏层维度通常等于词向量维度);具体计算步骤可见《通透理解FlashAttention与FlashAttention2:全面降低显存读写、加快计算速度》
正因为Transformer架构中注意力机制的二次复杂度,现有的ChatGPT等大模型处理长文本算力消耗巨大,因此:
1.有了针对注意力机制的各种所谓魔改,甚至也有S4、FlashAttention及其二代等;
2.S4、FlashAttention等作者提出了新的序列模型:Mamba,在很多语言任务上击败/匹配Transformer性能,具有线性复杂度和5倍推理吞吐量。
1.2 RNN
关于RMM,详见可见《如何从RNN起步,一步一步通俗理解LSTM》。每一个时刻的隐藏状态都是基于当前的输入
和前一个时刻的隐藏状态
计算得到的,比如泛化到任一时刻,便是
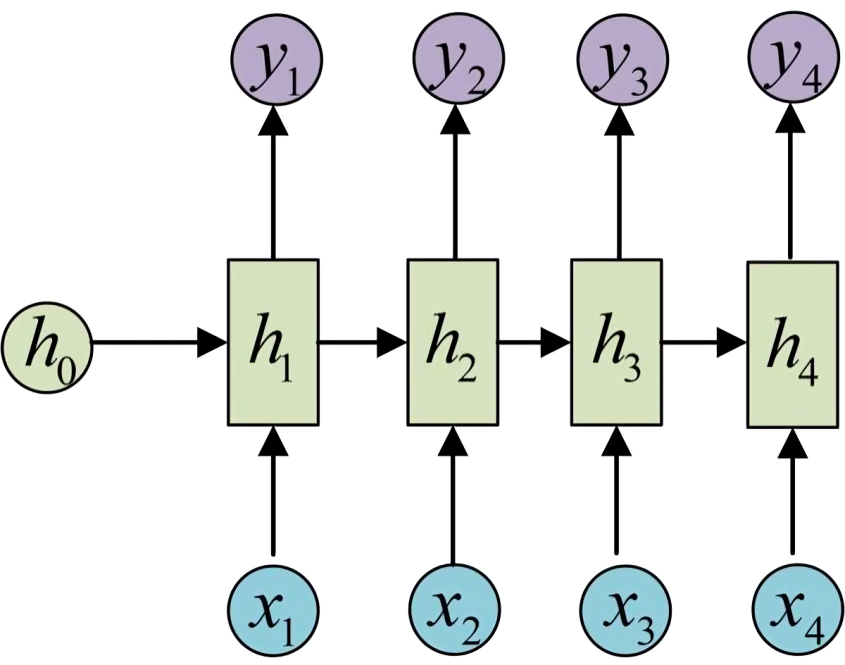
总之,RNN在序列中的每个时间步需要两个输入,即时间步的输入和前一个时间步的隐藏状态(a hidden state of the previous time step),以生成时的隐藏状态,最终预测输出(to generate the next hidden state and predict the output)。
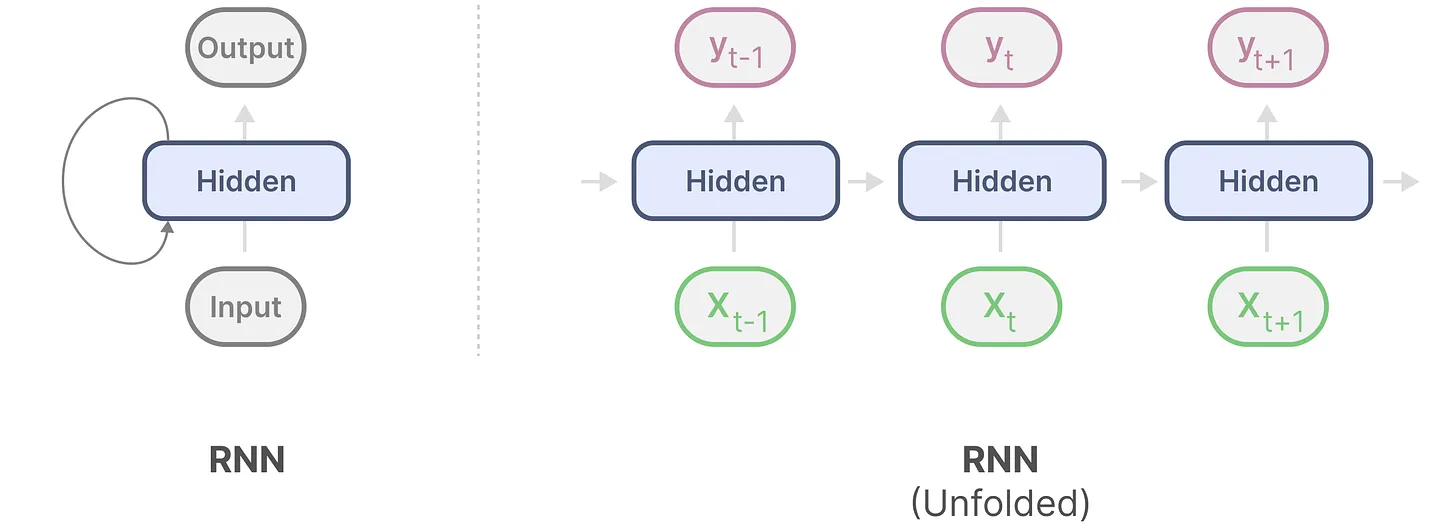
即,先根据输入
和前一时刻的隐藏状态
计算出最新的隐藏状态
,便可以根据最新的隐藏状态
预测出
了
至于为何要先介绍RNN呢,很快你就会明白了(RNN和SSM是一个本质)
RNN主要存在两个问题
- 第一个问题在于,虽然每个隐藏状态都是所有先前隐藏状态的聚合,然随着时间的推移,RNN 往往会忘记某一部分信息,比如下图最后一个隐藏状态在生成名称“ Maarten”时不再包含有关单词“Hello”的信息(说白了,就是如此文所说的,在实践中,一般只包含前面若干步而非之前所有步的隐藏状态)
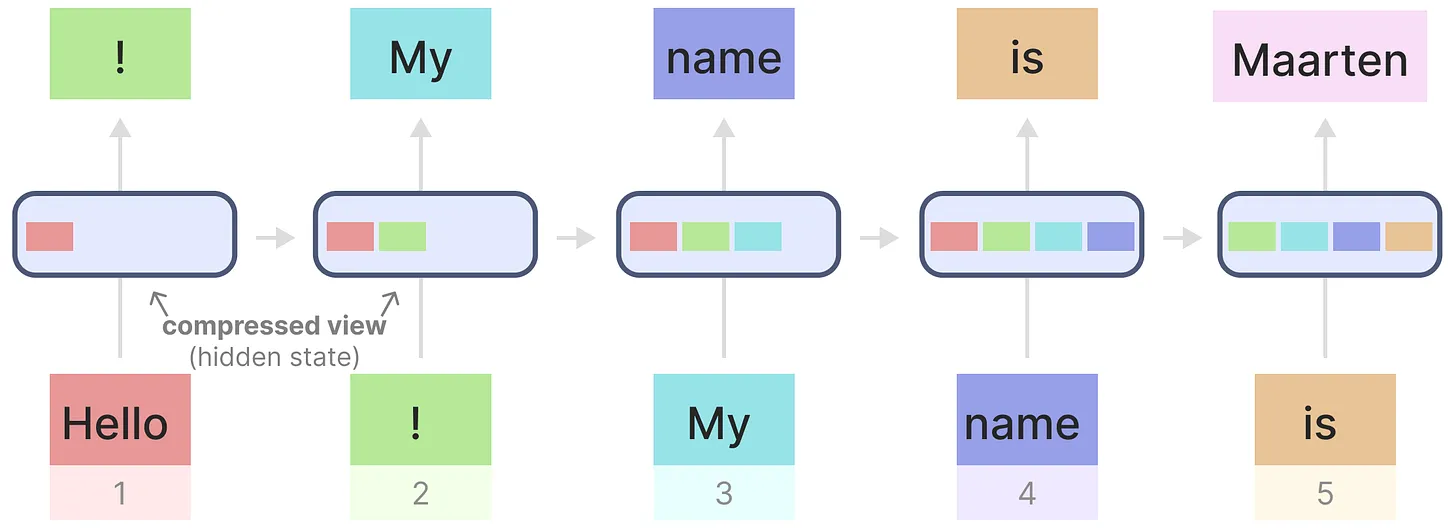
- 第二个问题在于,RNN没法并行训练,相当于推理快但训练慢。为何RNN没法并行训练?而且还写不成卷积形式(其实就是因为RNN多了一个非线性的转换函数,比如tanh)
1.3 什么是状态空间与SSM
mamba论文的一作Albert Gu多年来一直在推动SSM的发展:
- 他在SSM的基础上,通过此篇论文《Efficiently Modeling Long Sequences with Structured State Spaces》首次提出了结构化状态空间S4(这里有关于S4的更多论文),但这篇论文的可读性比较差;
- 当然,作者在YouTube上有一个关于这篇S4论文的精彩解读,比S4论文的可读性提高很多,且本文中也应用了其中的部分PPT截图,但还可以更加通俗易懂;
- 此外,Maarten Grootendorst写了一篇《A Visual Guide to Mamba and State Space Models》,可读性较强。
1.3.1 什么是状态空间
想象一下我们正在穿过一个迷宫,图中每个小框代表迷宫中的一个位置,并附有某个隐式的信息,例如你距离出口有多远
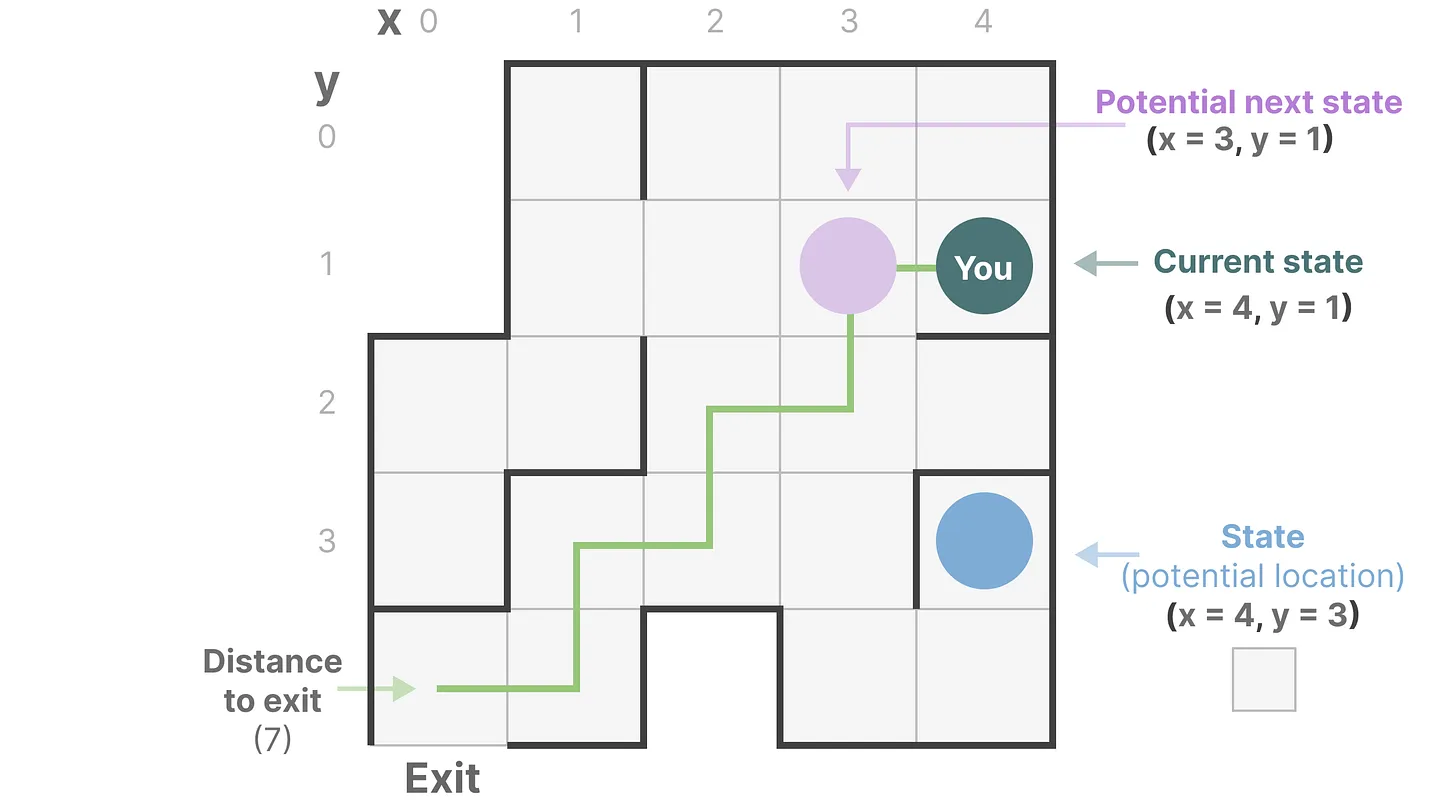
而上述迷宫可以简化建模为一个“状态空间表示state space representation”,每一个小框显示
- 你当前所在的位置(当前状态current state)
- 下一步可以去哪里(未来可能的状态possible future states)
- 以及哪些变化会将你带到下一个状态(向右或向左)
而描述状态的变量(在我们的示例中为 X 和 Y 坐标以及到出口的距离)可以表示为“状态向量state vectors”
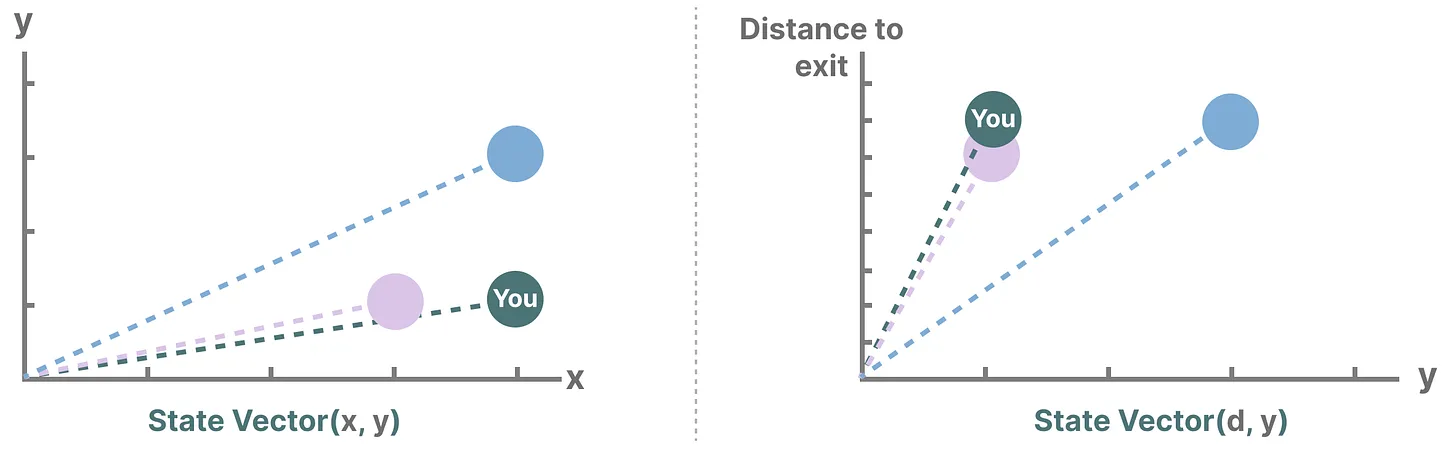
1.3.2 什么是状态空间模型SSM——RNN本质就是一个SSM
SSM 是用于描述这些状态表示并根据某些输入预测其下一个状态可能是什么的模型
一般SSMs包括以下组成
- 映射输入序列x(t),比如在迷宫中向左和向下移动
- 到潜在状态表示h(t),比如距离出口距离和 x/y 坐标
- 并导出预测输出序列y(t),比如再次向左移动以更快到达出口
然而,它不使用离散序列(如向左移动一次),而是将连续序列作为输入并预测输出序列

SSM 假设系统(例如在 3D 空间中移动的物体)可以通过两个方程从其在时间 时的状态进行预测「 当然,其实下面第一个方程表示成这样可能更好:
,不然容易引发歧义 」
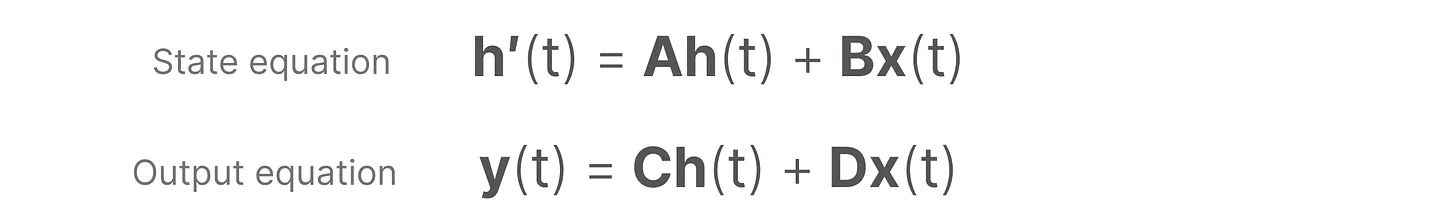
然后,请你再细品一下
- 上面的第一个方程是不和RNN循环结构:
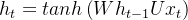 非常类似:通过上一个隐藏状态和当前输入综合得到当前的隐藏状态,只是两个权重W、U换成了A、B两个系数,且去掉了非线性的激活函数tanh
非常类似:通过上一个隐藏状态和当前输入综合得到当前的隐藏状态,只是两个权重W、U换成了A、B两个系数,且去掉了非线性的激活函数tanh - 但系数A代表着什么,这点其实非常关键,然我看过的几乎所有讲解SSM/S4/mamba的文章都没有一针见血的指出来,其实A就是存储着之前所有历史信息的浓缩精华(可以通过一系列系数组成的矩阵表示之),以基于A更新下一个时刻的空间状态hidden state
总之,通过求解这些方程,可以根据观察到的数据:输入序列和先前状态,去预测系统的未来状态
1.3.3 SSM的两个方程:状态方程与输出方程
总之,SSM的关键是找到:状态表示(state representation)—— ,以便结合「其与输入序列」预测输出序列

而这两个方程也是状态空间模型的核心( 此时在SSM中,即便是在不同的输入之下,矩阵A、B、C、D都还是固定不变的,但到了后续的改进版本mamba中则这4个矩阵都是随着输入不同而可变的参数)
- 第一个方程:状态方程,矩阵B与输入x(t)相乘之后,再加上矩阵A与前一个状态h(t)相乘的结果
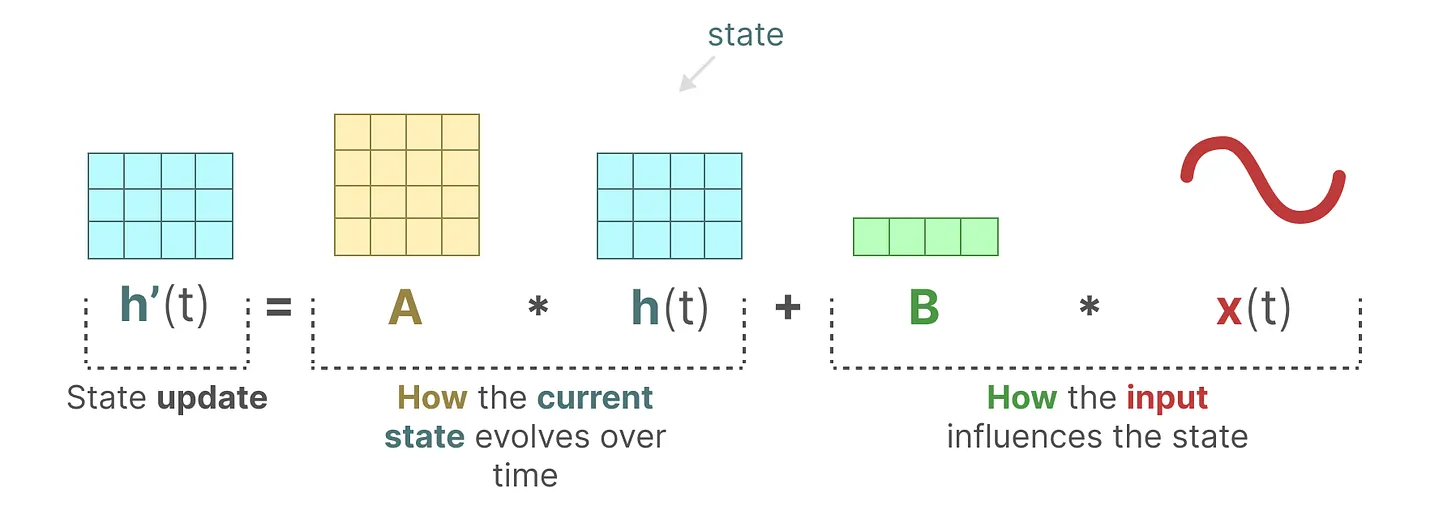
换言之,矩阵影响输入
,
矩阵影响前一个状态
,而
指的是任何给定时间
的潜在状态表示(latent state representation),而
指的是某个输入「当然,还是上面那句话,表示成这样更好:
」
- 第二个方程:输出方程,描述了状态如何转换为输出(通过矩阵
),以及输入如何影响输出(通过矩阵
)
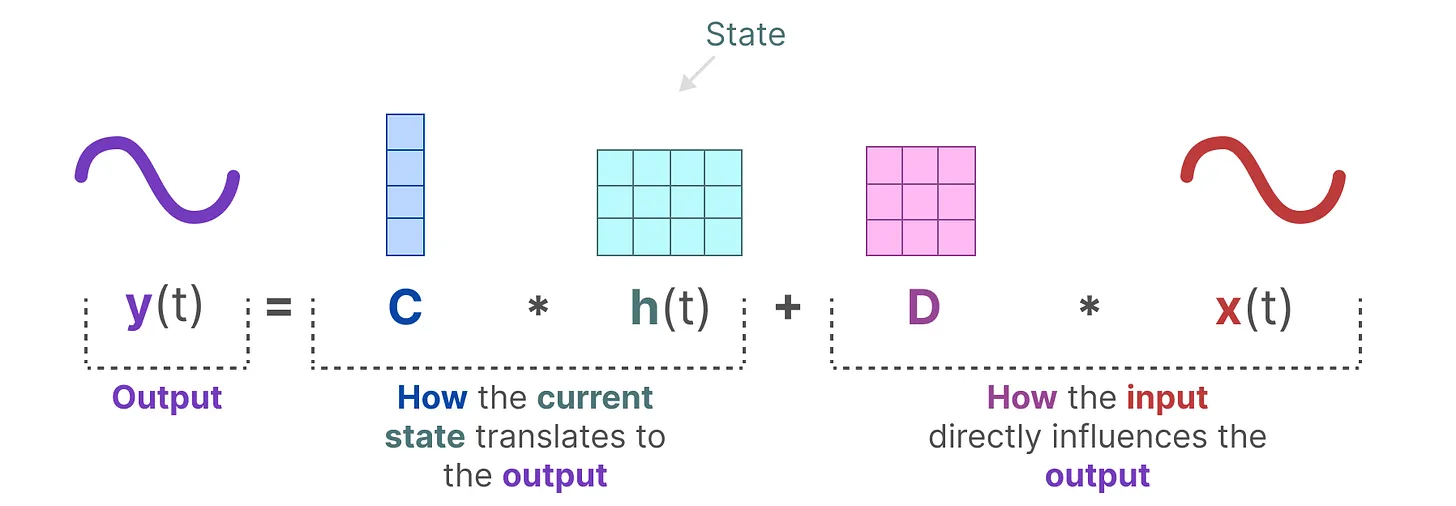
1.3.4 建立对SSM中两个核心方程的统一视角
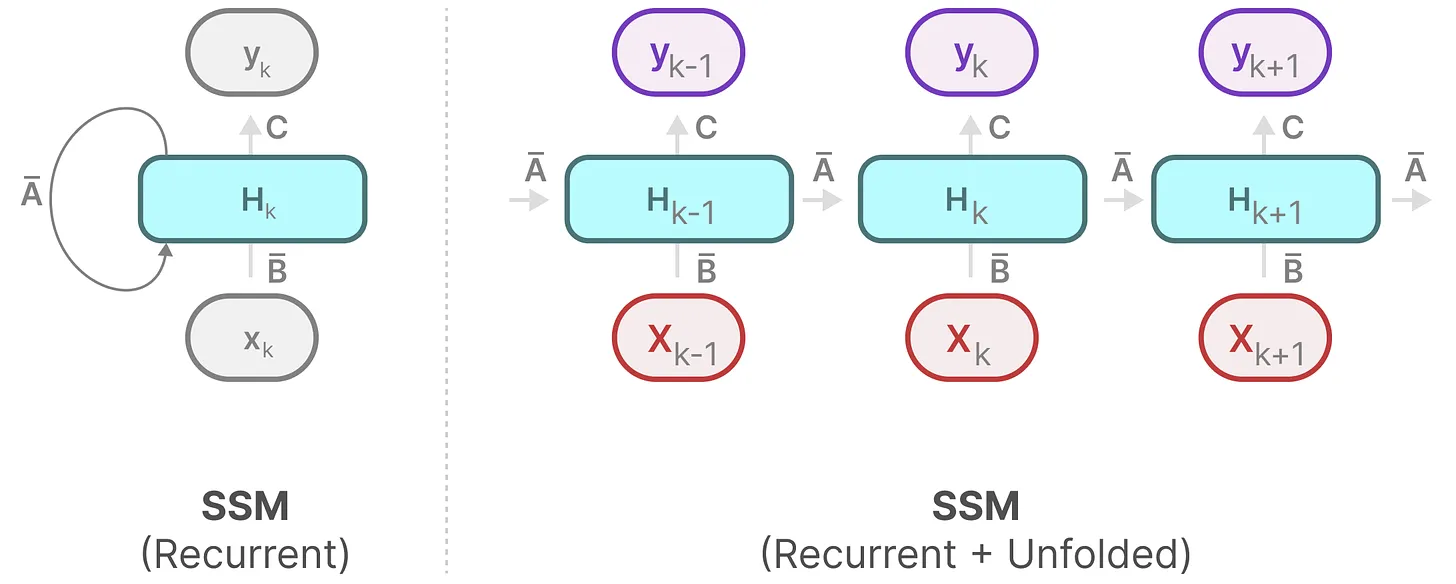
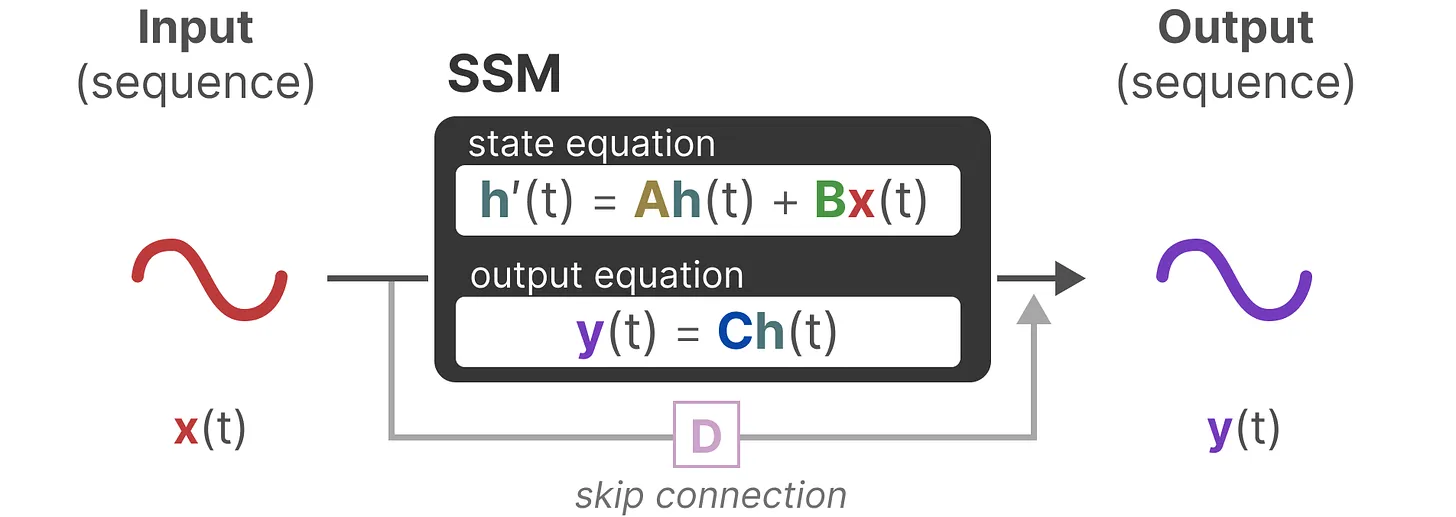
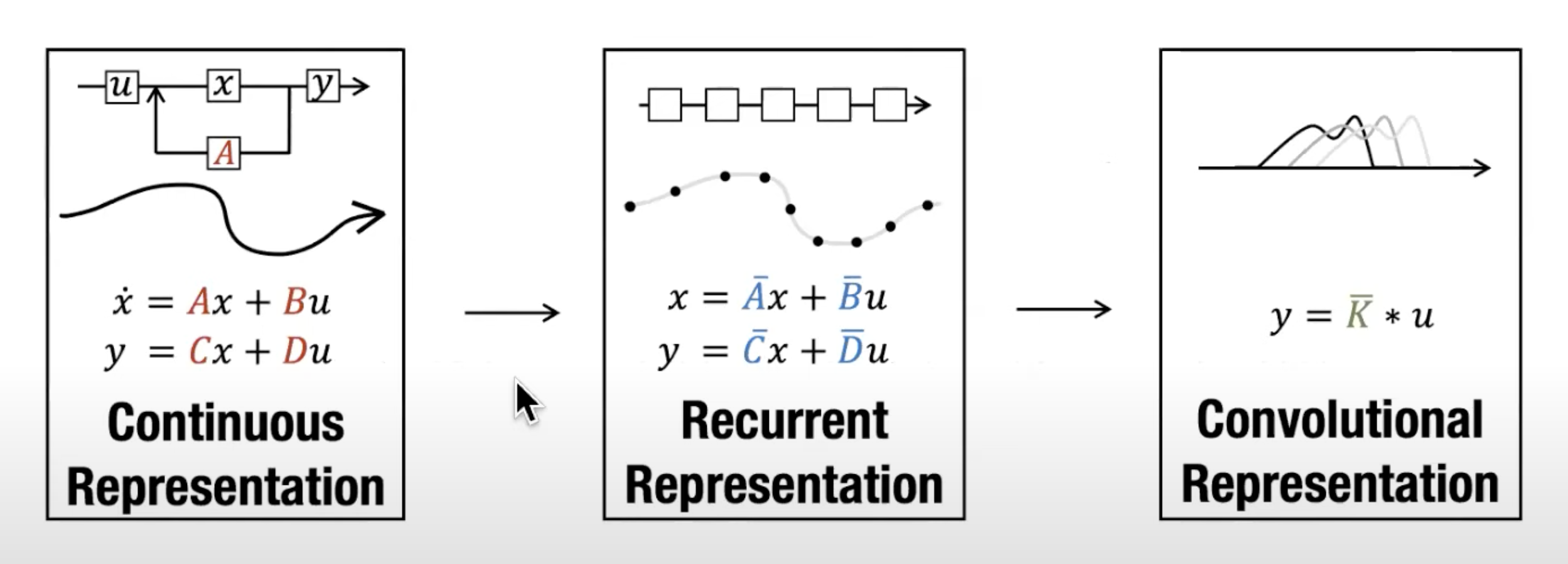
最终,我们可以通过下图统一这两个方程
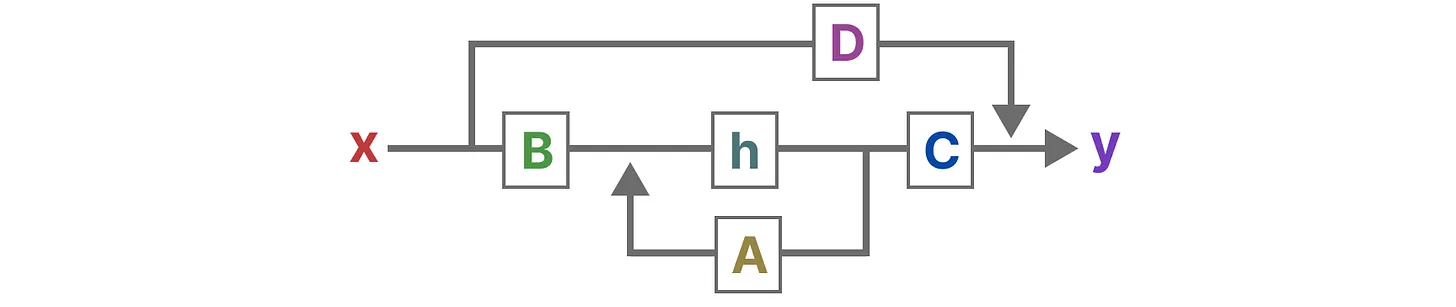
为了进一步加深对该图的理解,我们一步一步拆解下
1.假设我们有一些输入信号,该信号首先乘以矩阵

2.上面第一步的结果,加上:上一个状态与矩阵相乘(矩阵
描述了所有内部状态如何连接)的结果,用来更新状态state
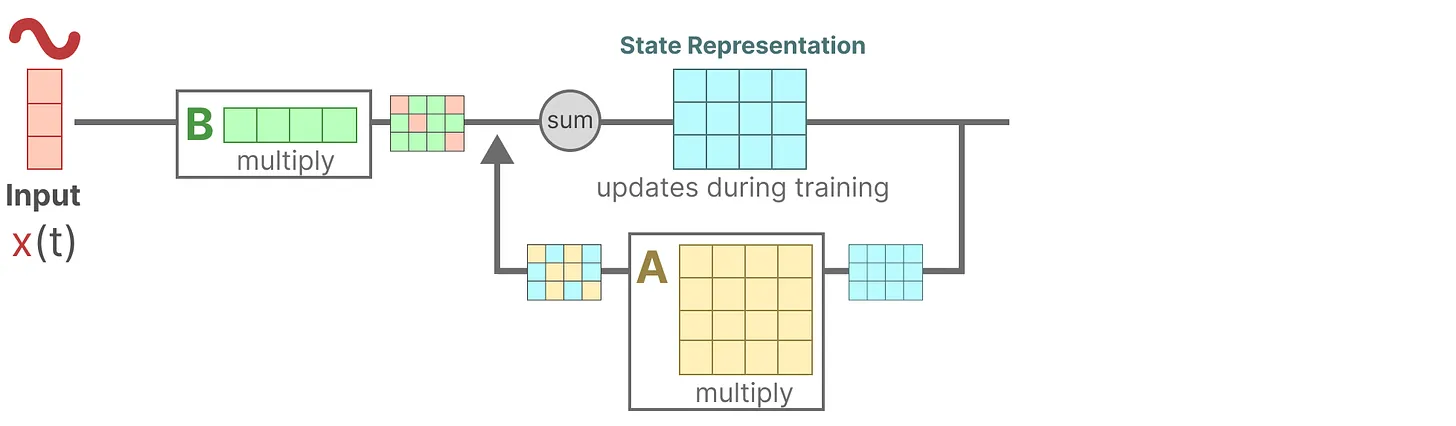
3.然后,使用矩阵来将状态转换为输出
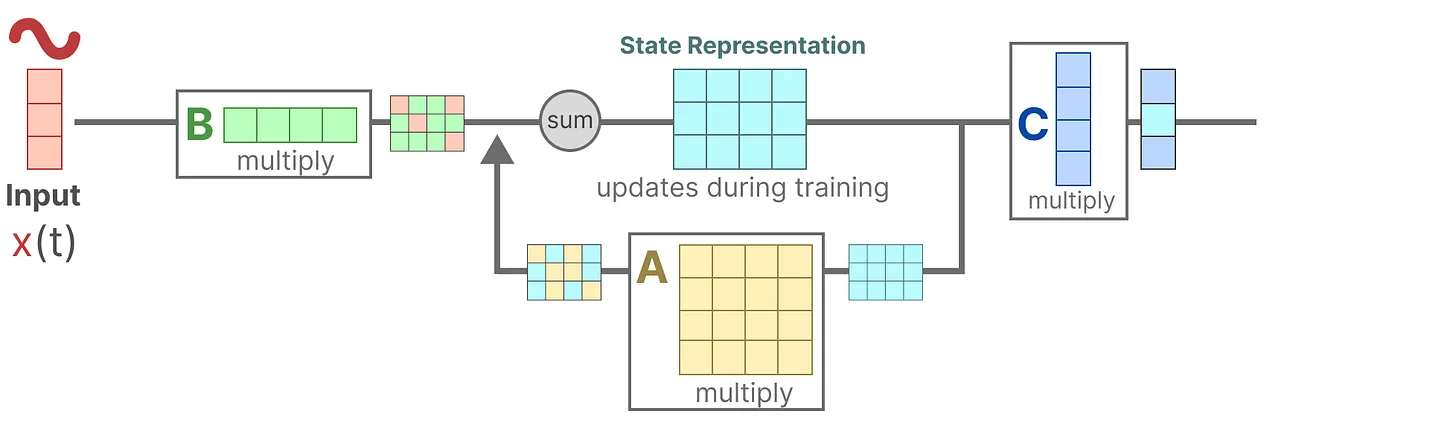
4.最后,再利用矩阵提供从输入到输出的直接信号,这通常也称为跳跃连接skip-connection
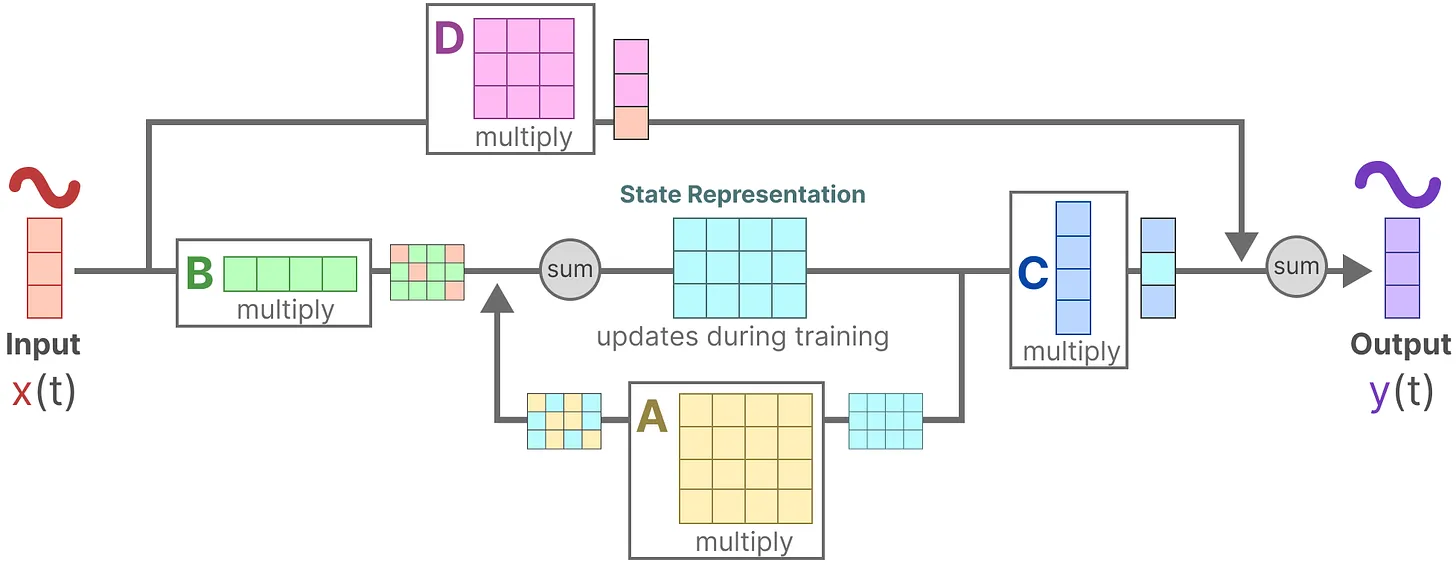
5.由于矩阵类似于跳跃连接,因此在没有跳跃连接的情况下,SSM 通常被视为如下
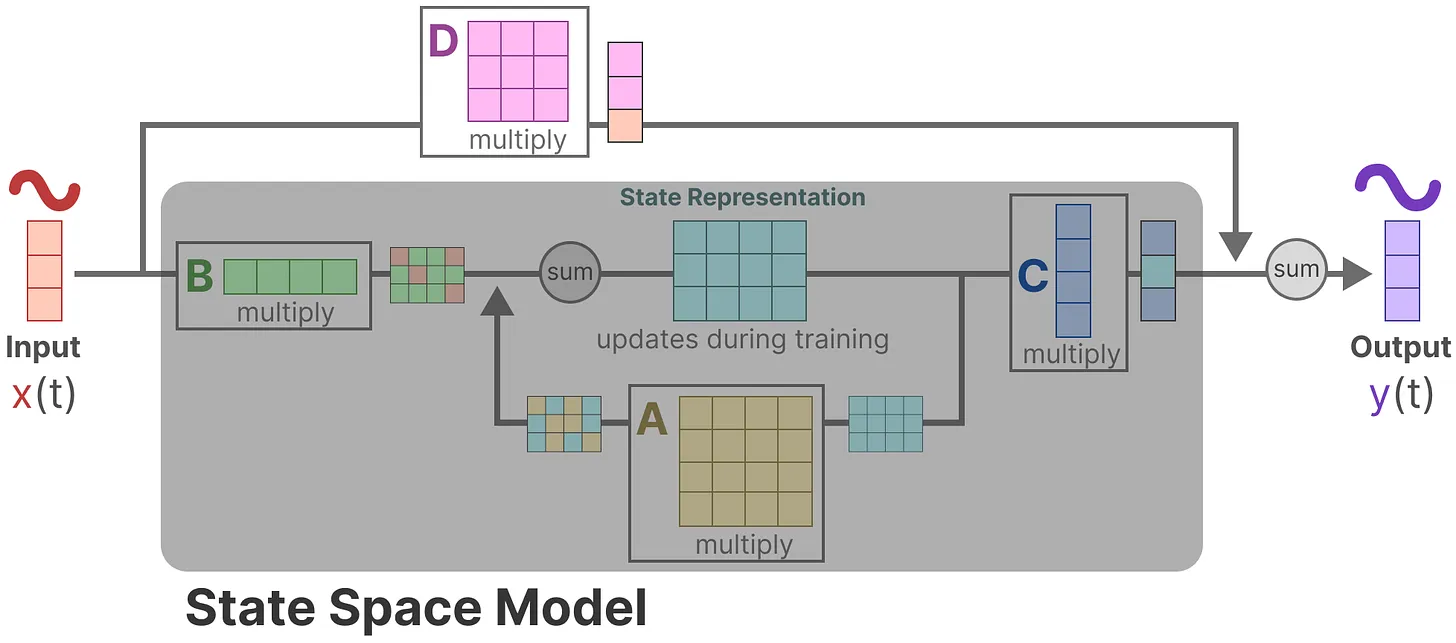
回到我们的简化视角,现在可以关注只矩阵构建的SSM核心
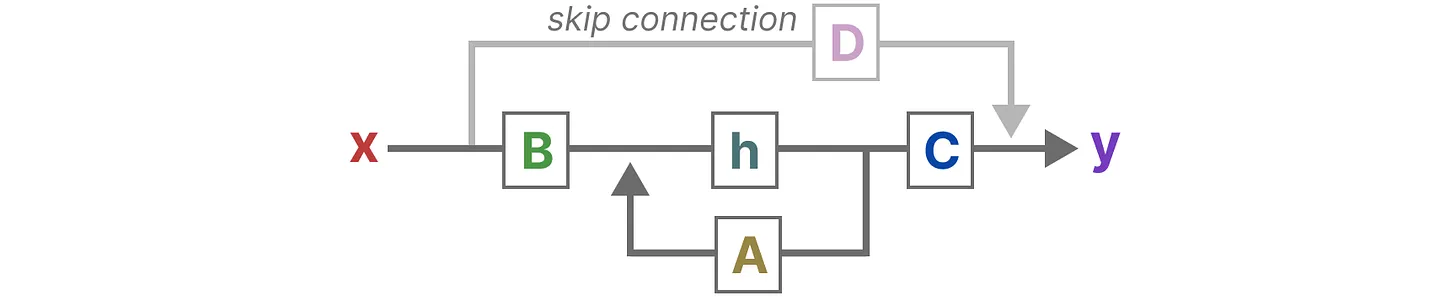
总之,这两个方程共同旨在根据观测数据预测系统的状态,且考虑到输入一般都是连续的,因此SSM的主要表示是连续时间表示( continuous-time representation )
2. 从 SSM到S4的升级之路
2.1 SSM到S4的三步升级:离散化SSM、循环/卷积表示、基于HiPPO处理长序列
2.1.1 离散数据的连续化:基于零阶保持技术做连续化并采样
由于除了连续的输入之外,还会通常碰到离散的输入(如文本序列),不过,就算SSM在离散数据上训练,它仍能学习到底层蕴含的连续信息,因为在SSM眼里,sequence不过是连续信号signal的采样,或者说连续的信号模型是离散的序列模型的概括
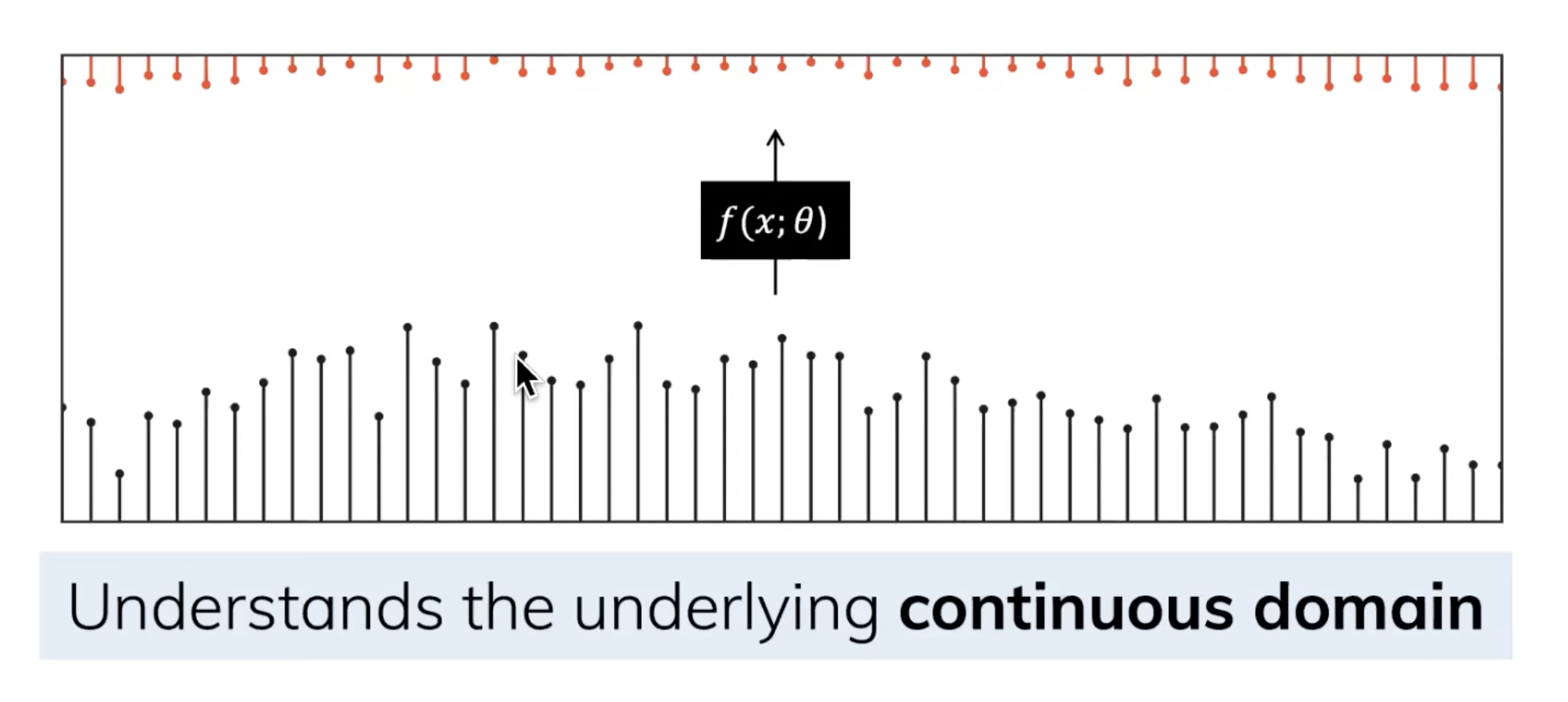
那模型如何处理离散化数据呢?答案是可以利用零阶保持技术(Zero-order hold technique)
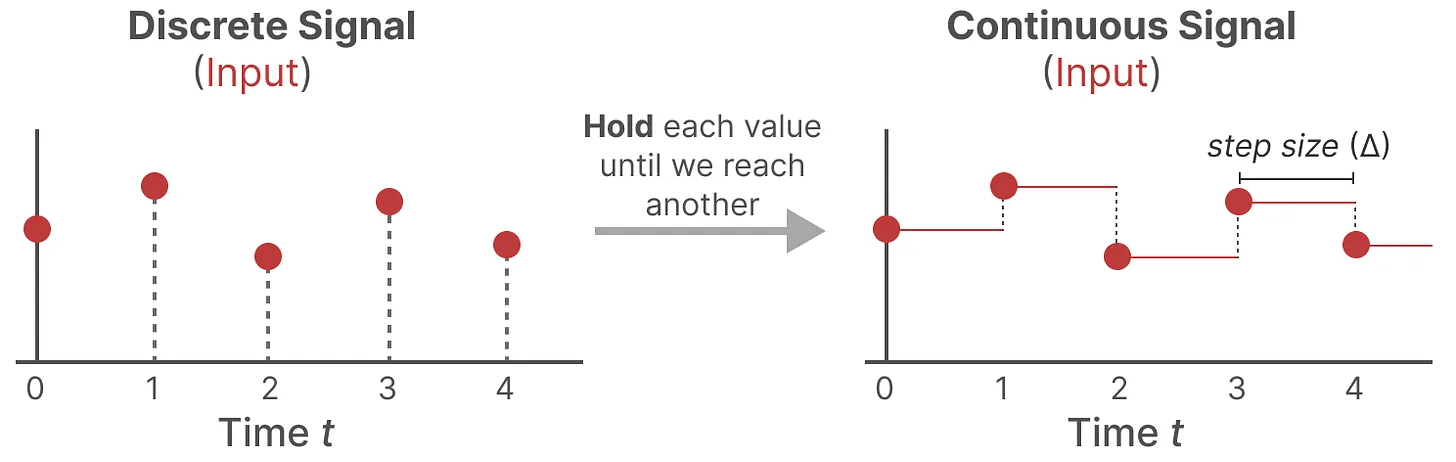
- 首先,每次收到离散信号时,我们都会保留其值,直到收到新的离散信号,如此操作导致的结果就是创建了 SSM 可以使用的连续信号
- 保持该值的时间由一个新的可学习参数表示,称为步长(siz)——
,它代表输入的阶段性保持(resolution)
- 有了连续的输入信号后,便可以生成连续的输出,并且仅根据输入的时间步长对值进行采样
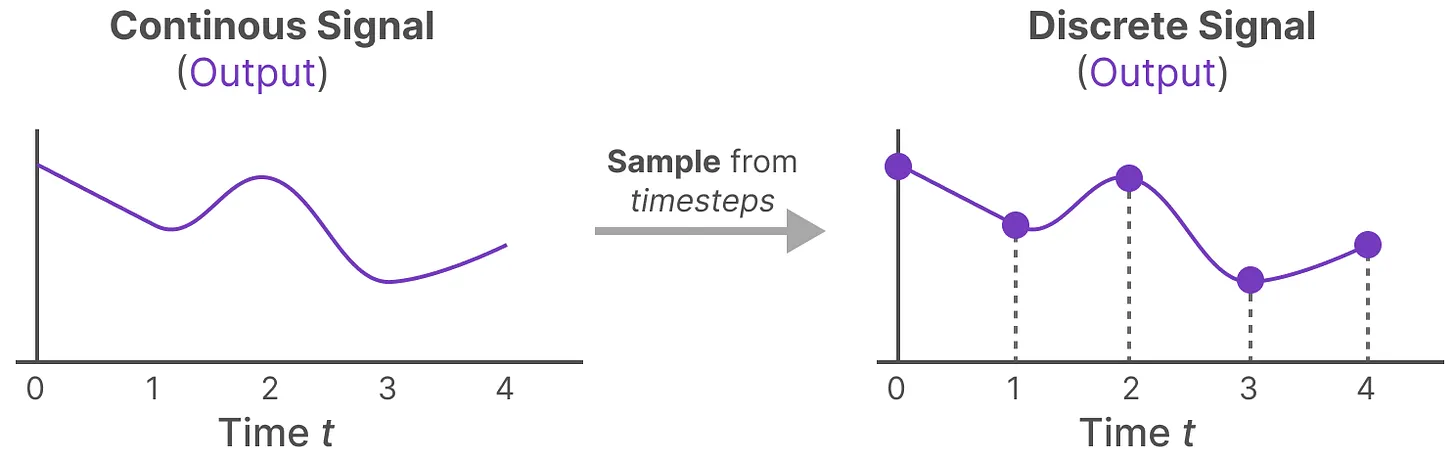
这些采样值就是我们的离散输出,且可以针对A、B按如下方式做零阶保持(做了零阶保持的在对应变量上面加了个横杠)
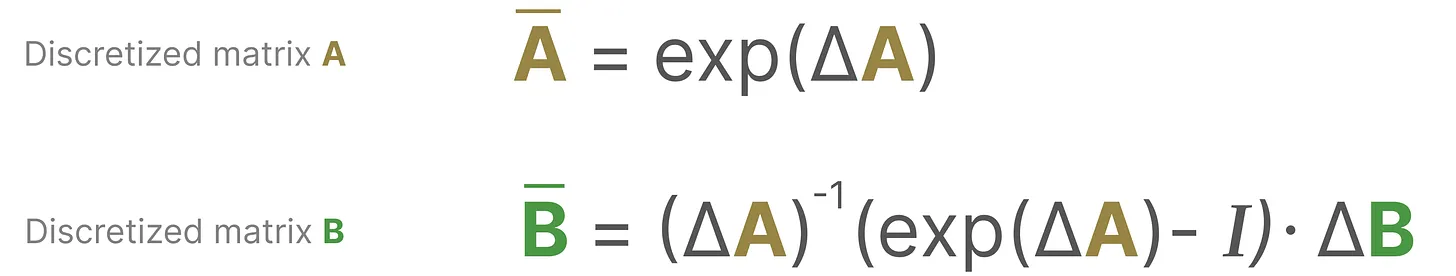
最终使我们能够从连续 SSM 转变为离散SSM,使得不再是函数到函数x(t) → y(t),而是序列到序列xₖ → yₖ,所以你看到,矩阵和
现在表示模型的离散参数,且这里使用
,而不是
来表示离散的时间步长
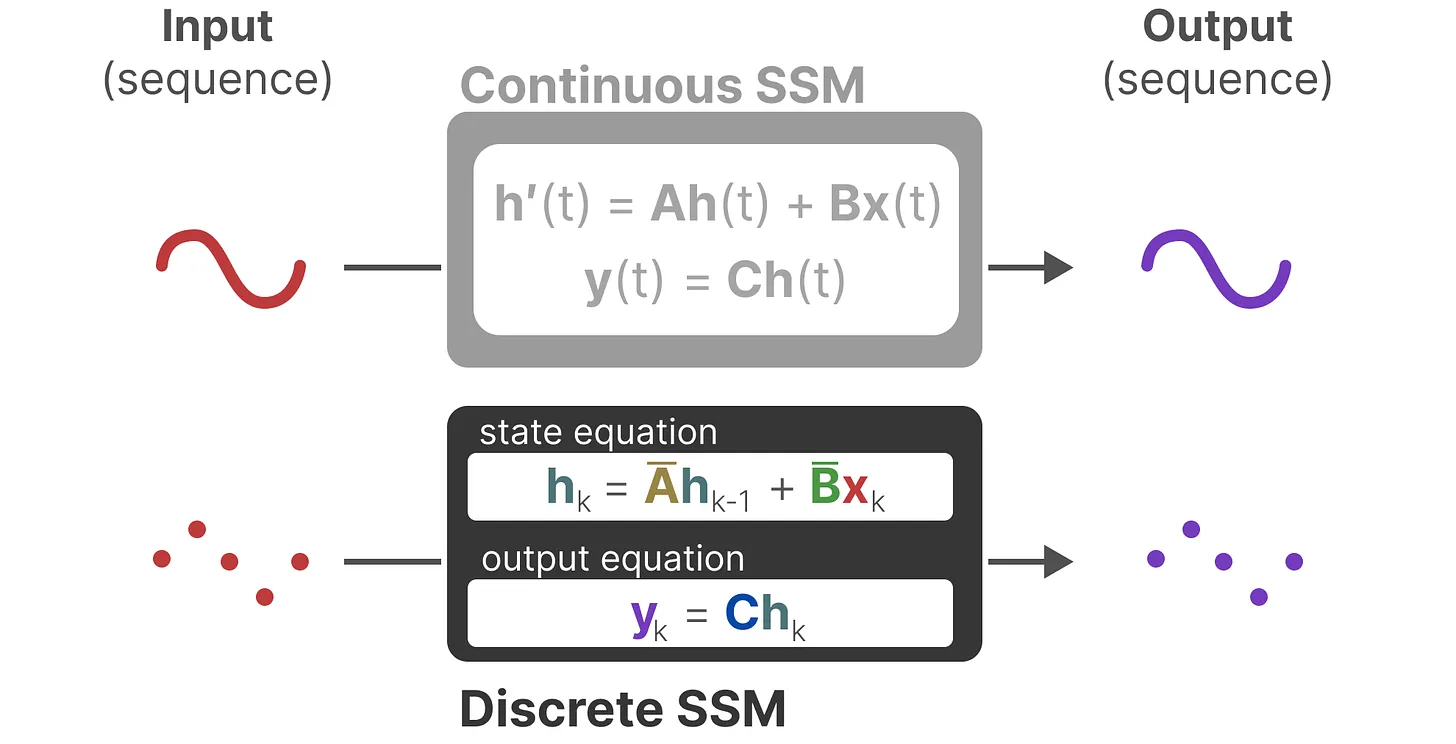
注意:我们在保存时,仍然保存矩阵的连续形式(而非离散化版本),只是在训练过程中,连续表示被离散化(During training, the continuous representation is discretized)
2.1.2 循环结构表示:方便快速推理
总之,离散 SSM 允许可以用离散时间步长重新表述问题
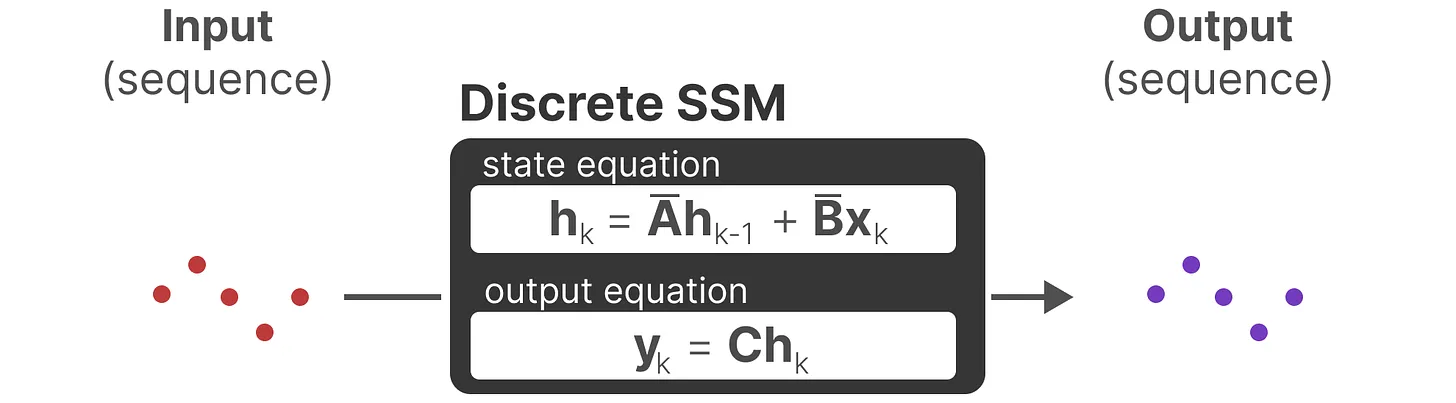
在每个时间步,都会涉及到隐藏状态的更新(比如取决于
和
的共同作用结果,然后通过
预测输出
)
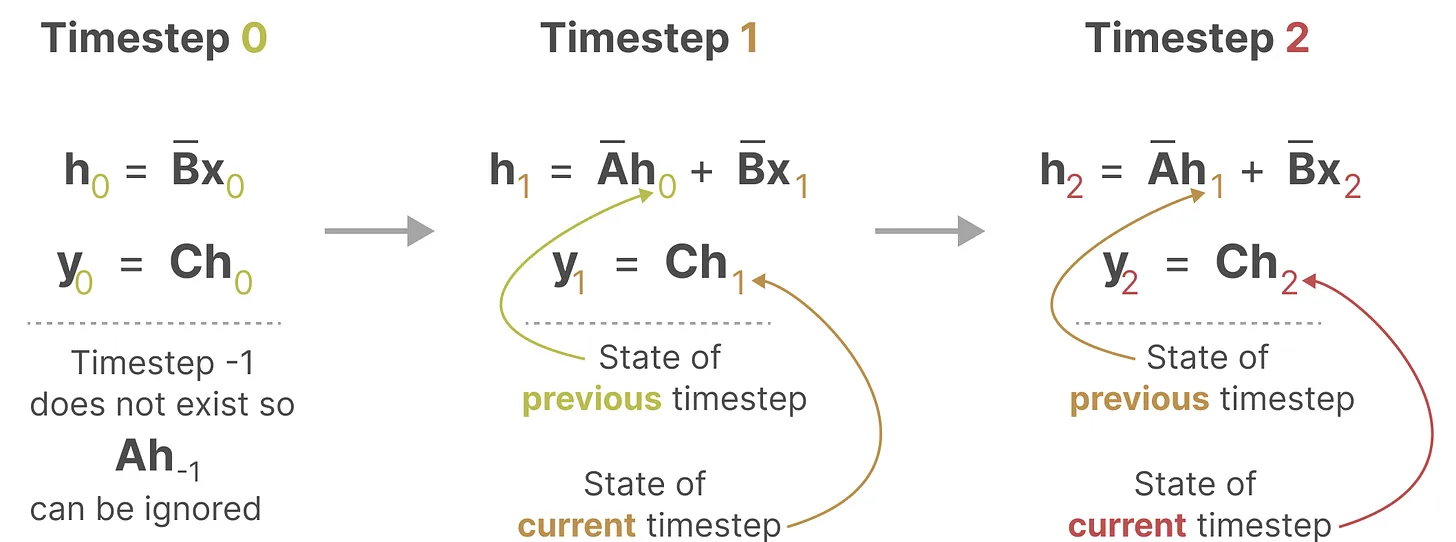
为方便理解其中的细节,再展开一下
如此,便可以RNN的结构来处理
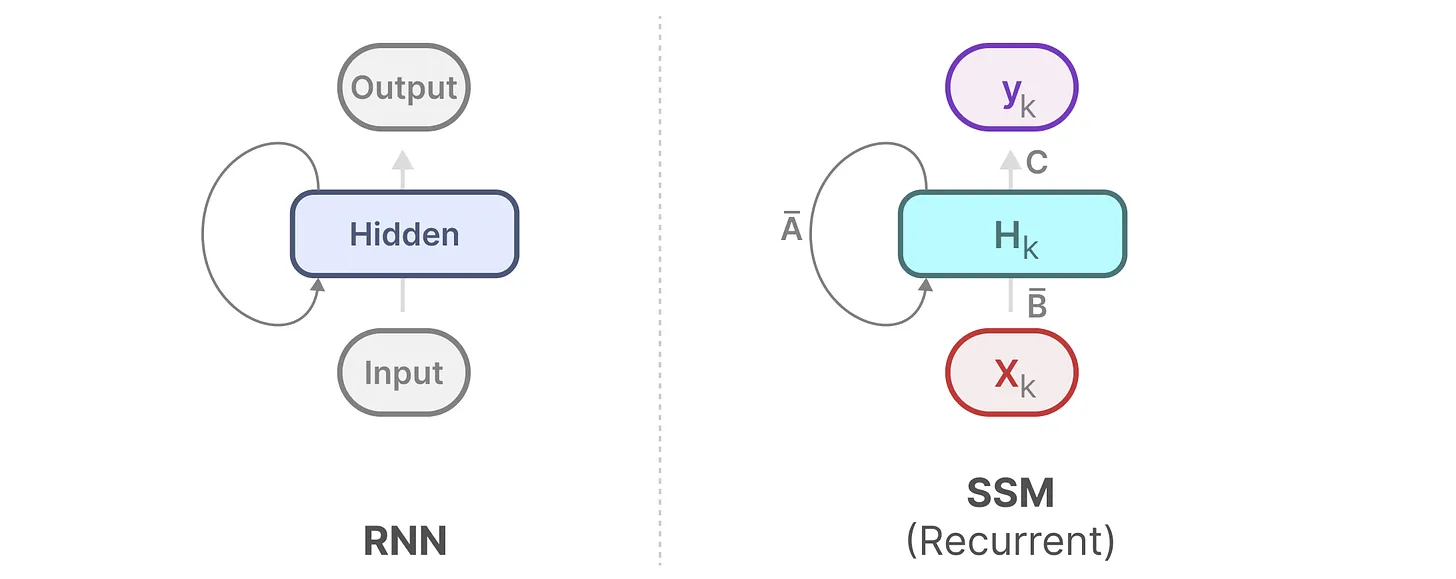
然后可以这样展开(其中,始终是
和
的共同作用之下更新的)
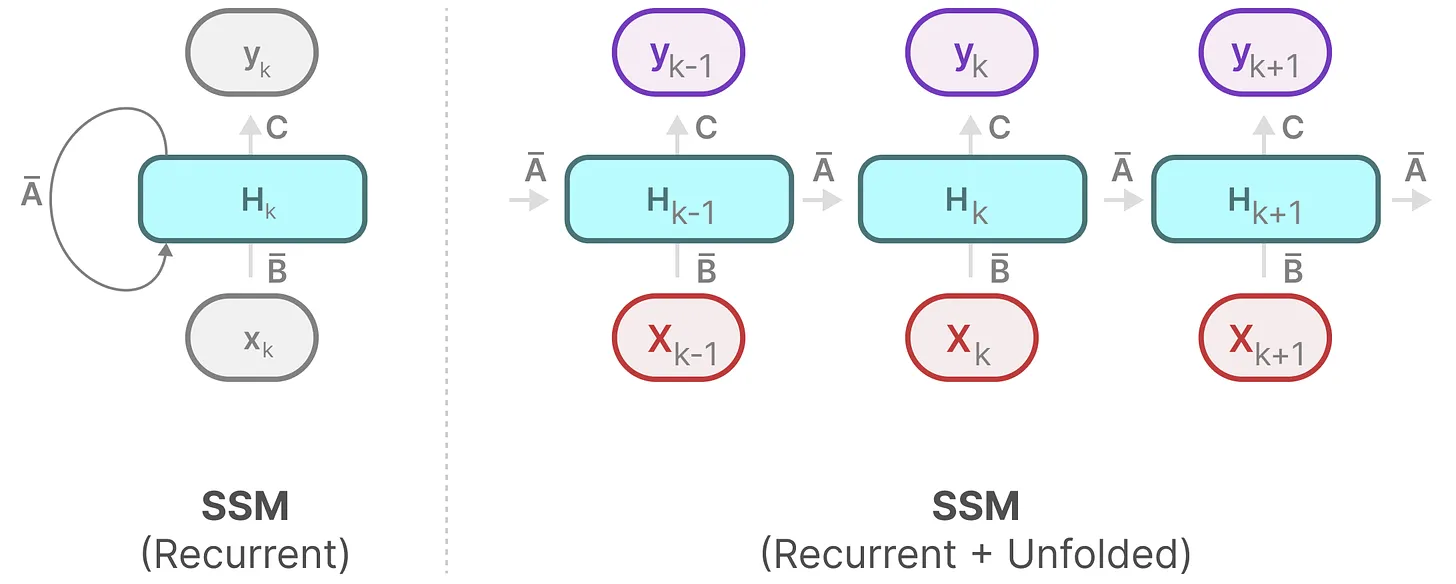
2.1.3 卷积结构表示:方便并行训练
在经典的图像识别任务中,我们用过滤器(即卷积核kernels)来导出聚合特征,而SSM也可以表示成卷积的形式
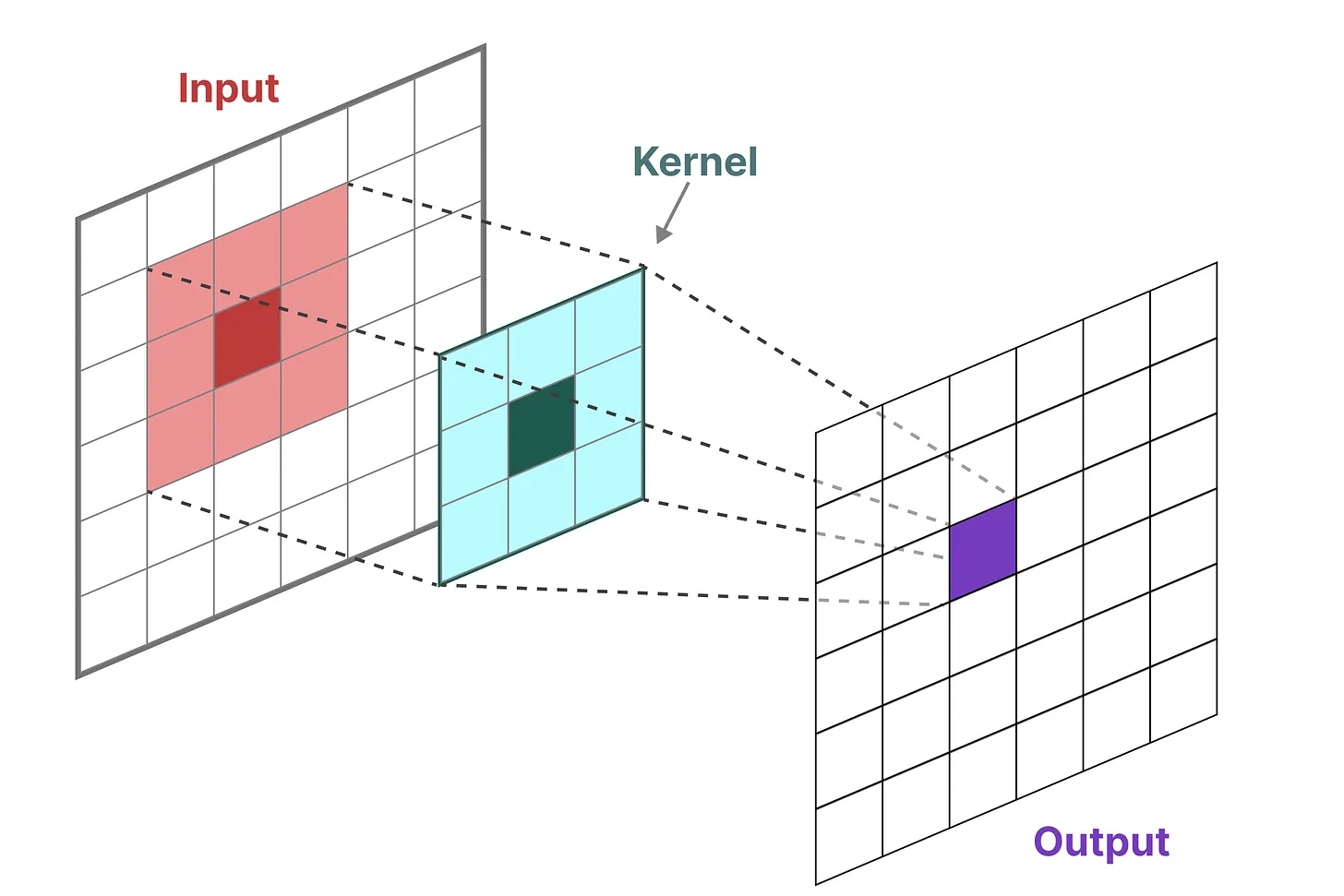
由于我们处理的是文本而不是图像,因此我们需要一维视角
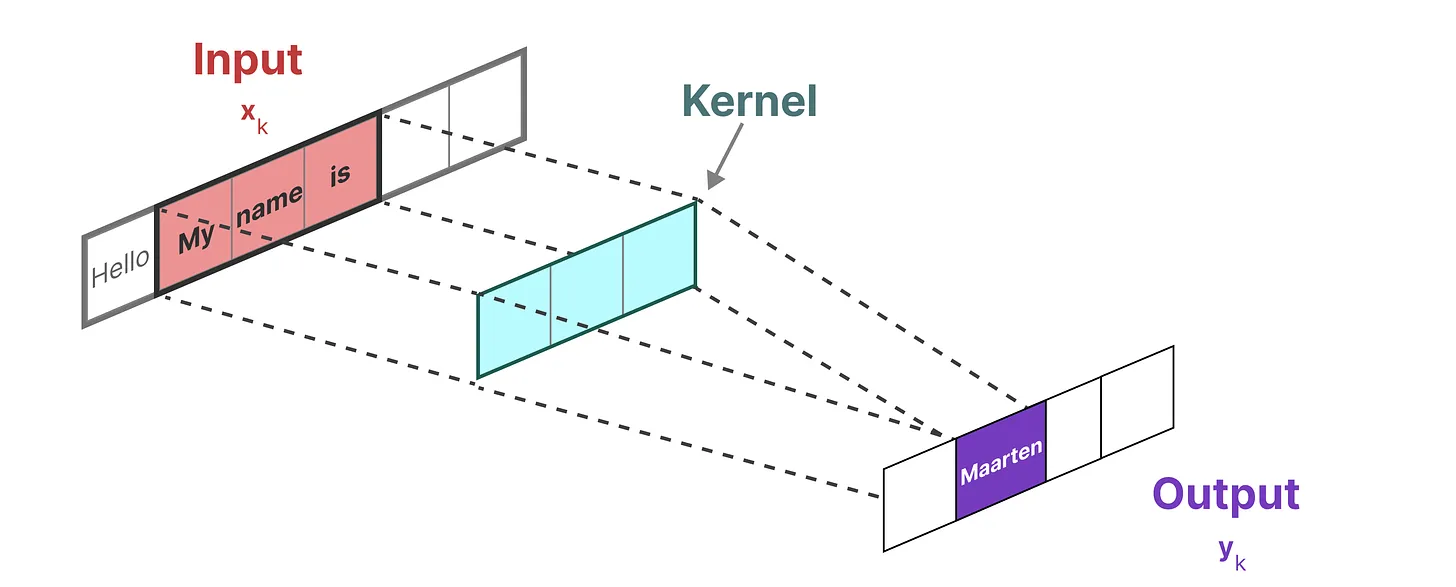
而用来表示这个“过滤器”的内核源自 SSM 公式
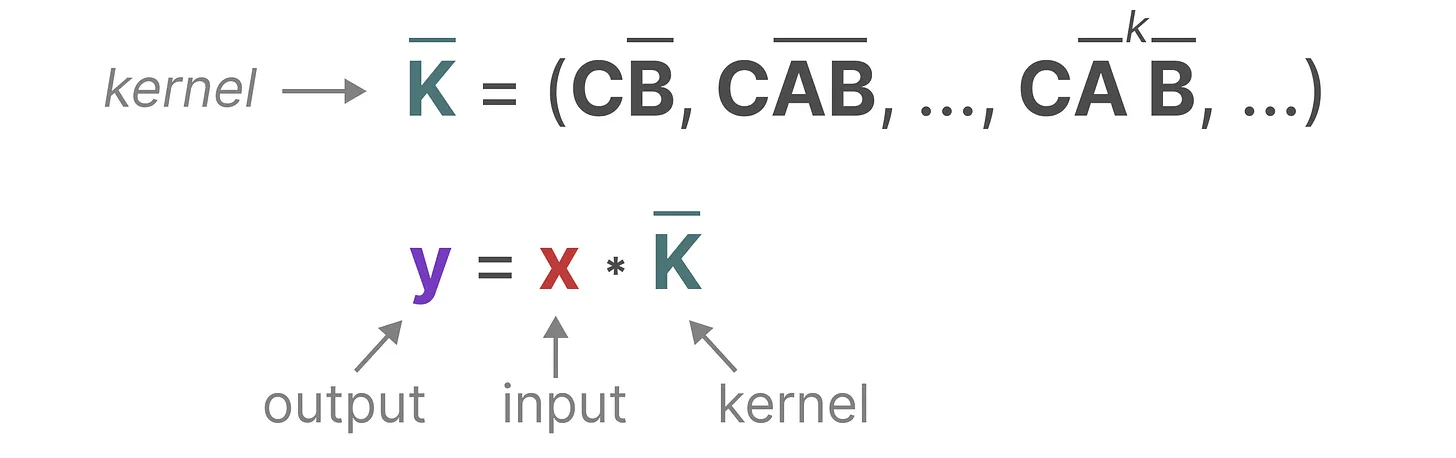
但怎么理解这个公式呢?一般的文章可能一带而过,但本文咱们还是通过一个例子一步一步理解
1.与卷积一样,我们可以使用 SSM 内核来检查每组token并计算输出
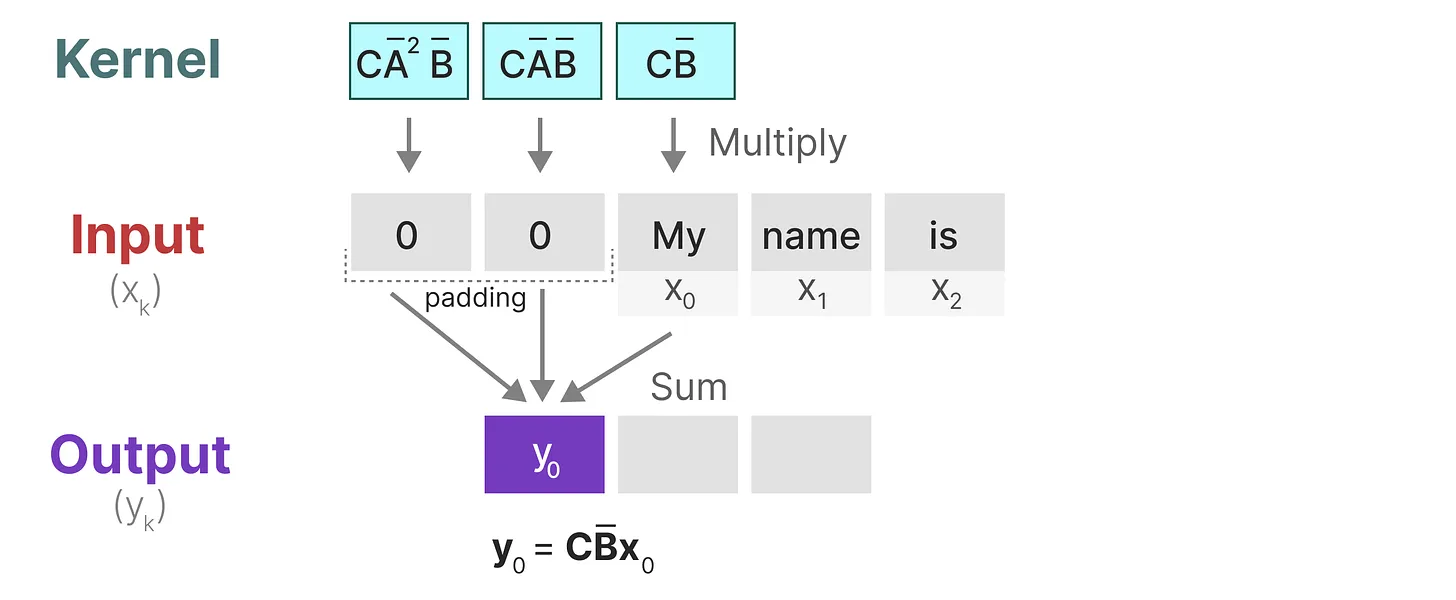
2.内核将移动一次以执行下一步的计算
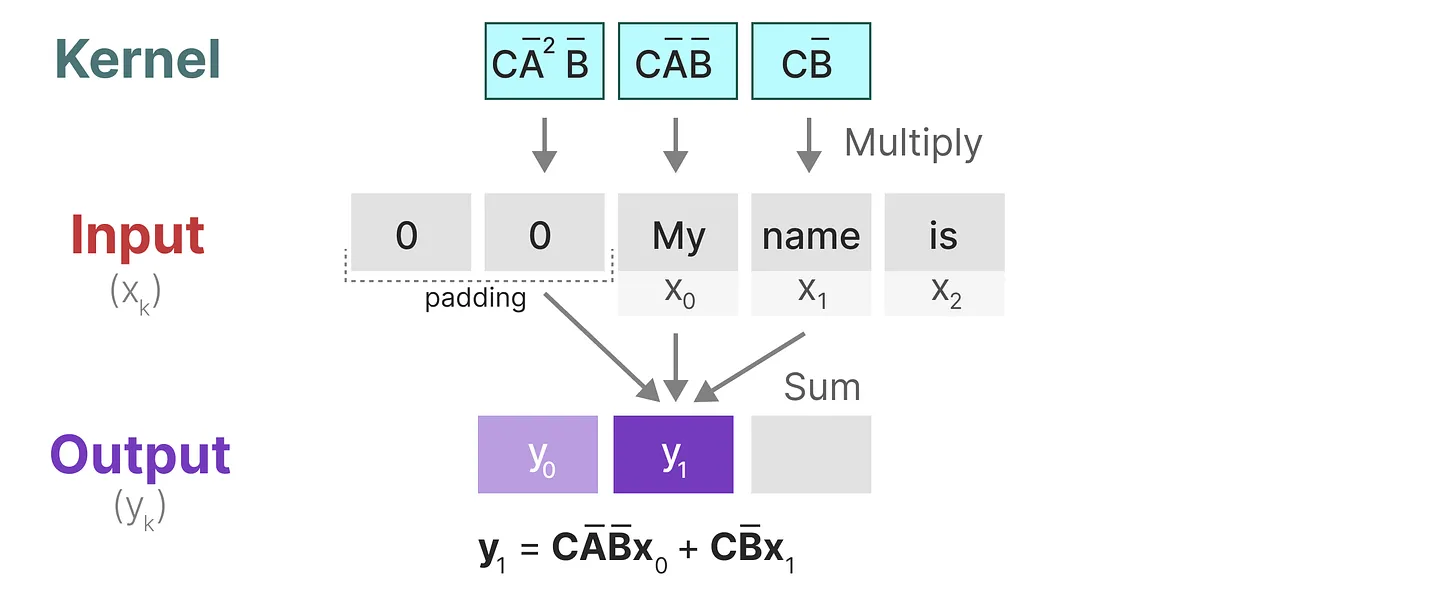
3.最后一步,我们可以看到内核的完整效果:
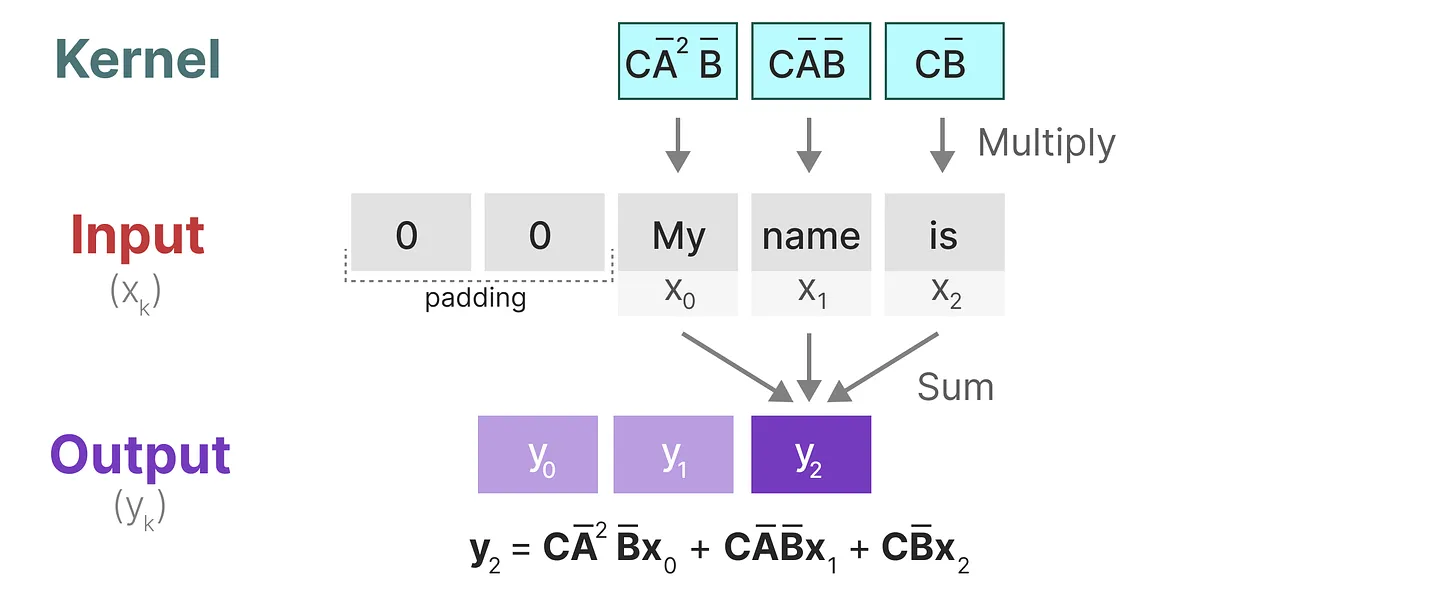
至于上图中的是咋计算得到的,别忘了我上面推导出来的
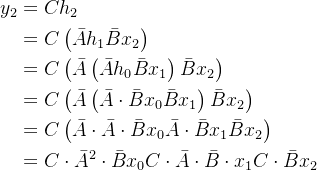
以此内推,可得
![]()
换个形式看,是不意味着实际上可以计算为点积,其中右侧向量是我们的输入
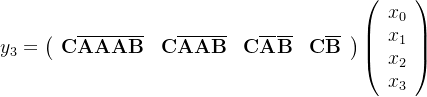
由于其中三个离散参数A、B、C都是常数,因此我们可以预先计算左侧向量并将其保存为卷积核,这为我们提供了一种使用卷积超高速计算的简单方法,如以下两个方程所示
![]()
至此,总结一下,将 SSM 表示为卷积的一个主要好处是它可以像卷积神经网络CNN一样进行并行训练。然而,由于内核大小固定,它们的推理不如 RNN 那样快速
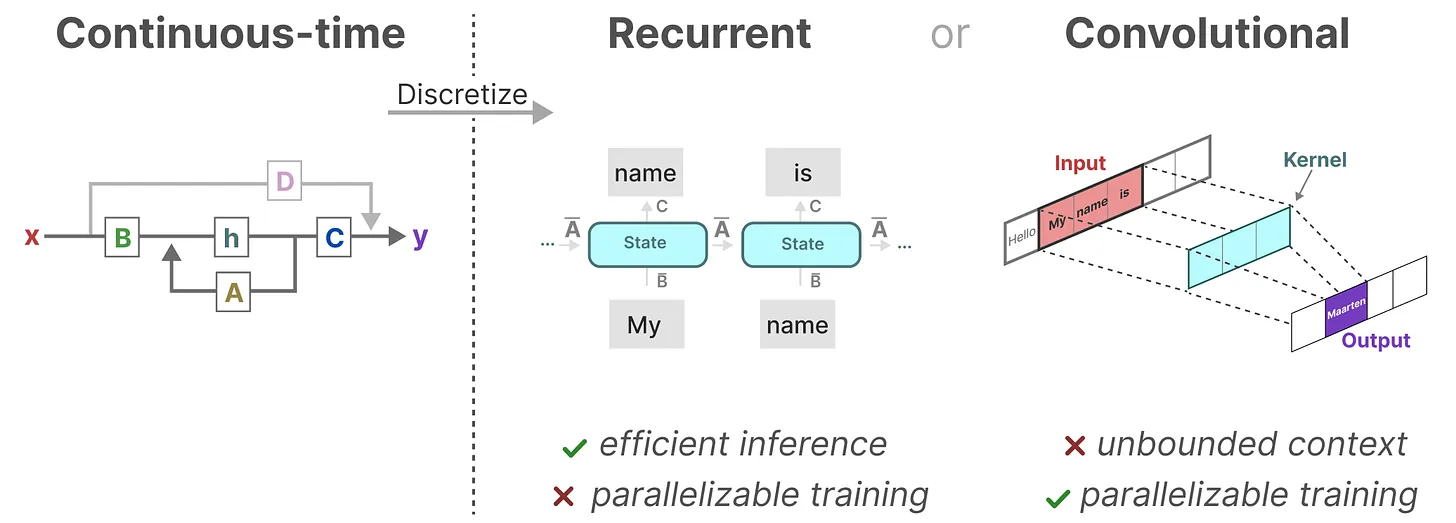
那有没两全其美的办法呢?最终是有的
1.作为从输入信号到输出信号的参数化映射,SSMs可以当做是RNN与CNN的结合「These models can be interpreted as acombination of recurrent neural networks (RNNs) and convolutional neural networks (CNNs)」,即推理用RNN结构,训练用CNN结构
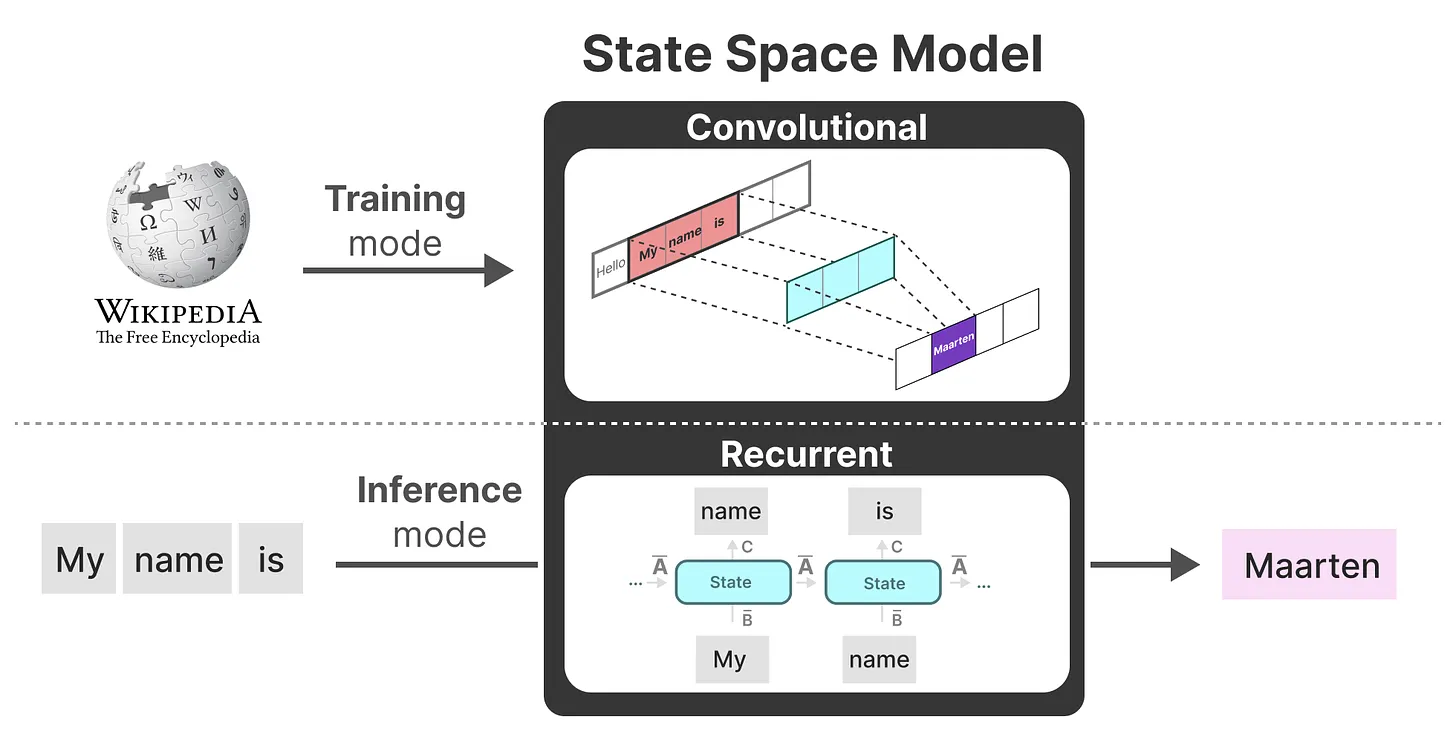
2.总之,这类模型可以非常高效地计算为递归或卷积,在序列长度上具有线性或近线性缩放(This class of models can be computed very efficiently as either arecurrence or convolution, with linear or near-linear scaling in sequence length)
2.1.4 长距离依赖问题的解决之道——HiPPO
如我们之前在循环表示中看到的那样,矩阵捕获先前previous状态的信息来构建新状态(
,当k = 5时,则有
)
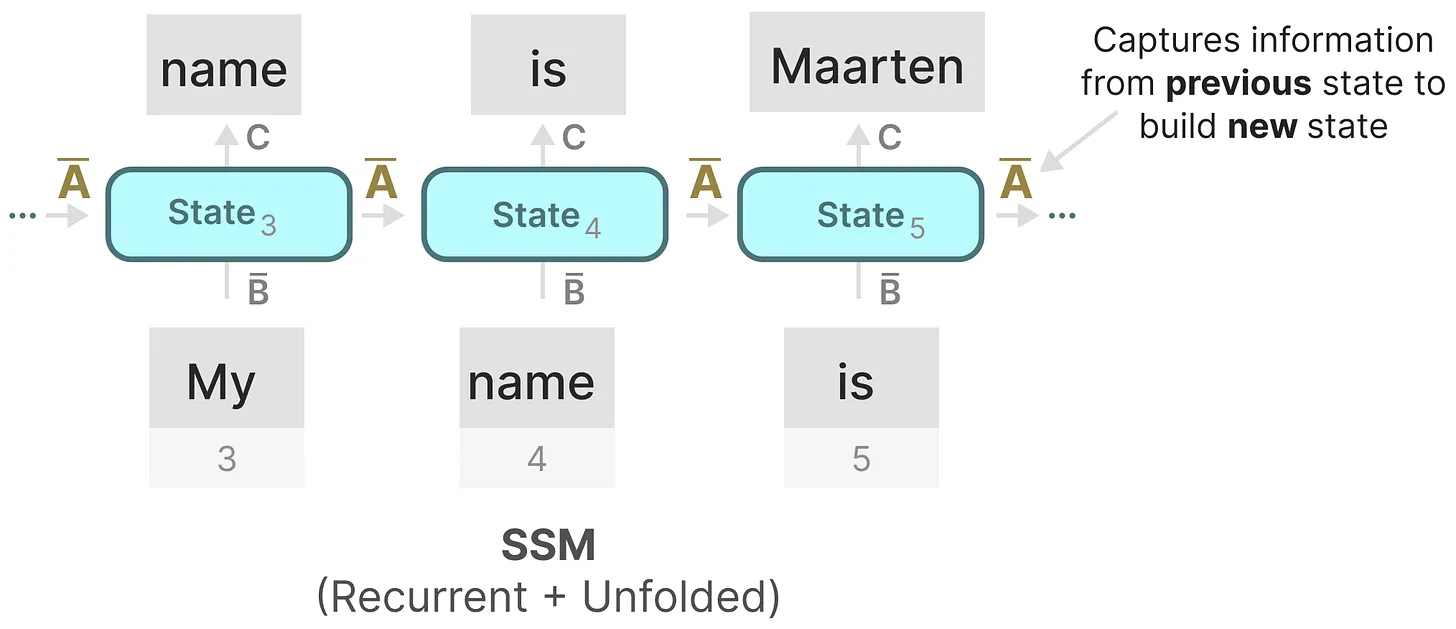
其实,某种意义上,算是矩阵A产生了隐藏状态(matrix A produces the hidden state)
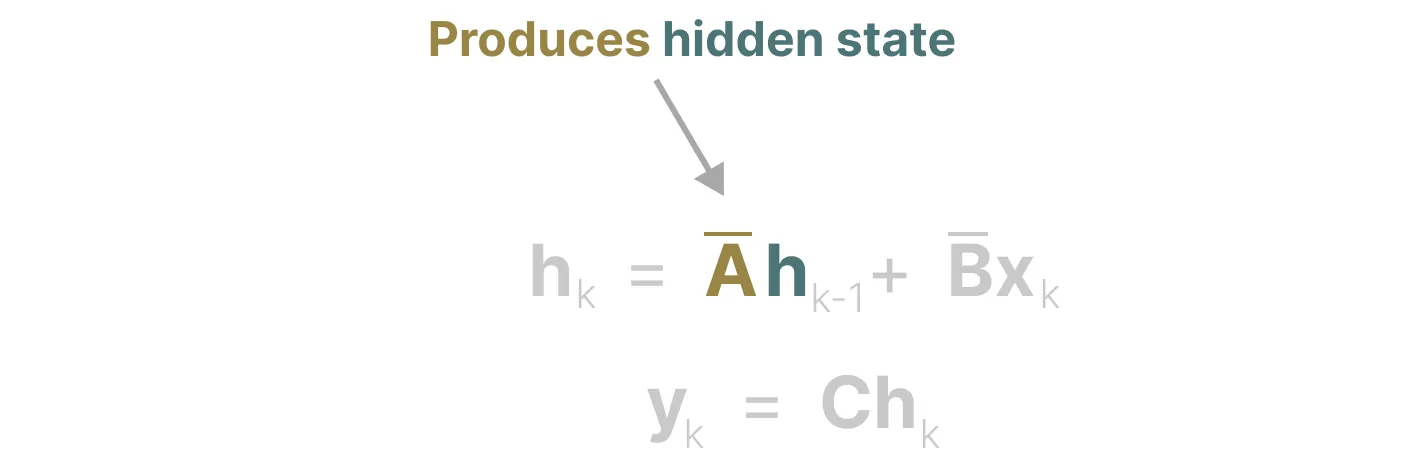
由于矩阵A只记住之前的几个token和捕获迄今为止看到的每个token之间的区别,特别是在循环表示的上下文中,因为它只回顾以前的状态
那么我们怎样才能以保留比较长的memory的方式创建矩阵A呢?
- 答案是可以使用Hippo(Hippo的全称是High-order Polynomial Projection Operator,其对应的论文为:HiPPO: Recurrent Memory with Optimal Polynomial Projections),解决如何在有限的存储空间中有效地解决序列建模的长距离依赖问题
- HiPPO尝试将当前看到的所有输入信号压缩为系数向量(HiPPO attempts to compress all input signals it has seen thus far into a vector of coefficients)
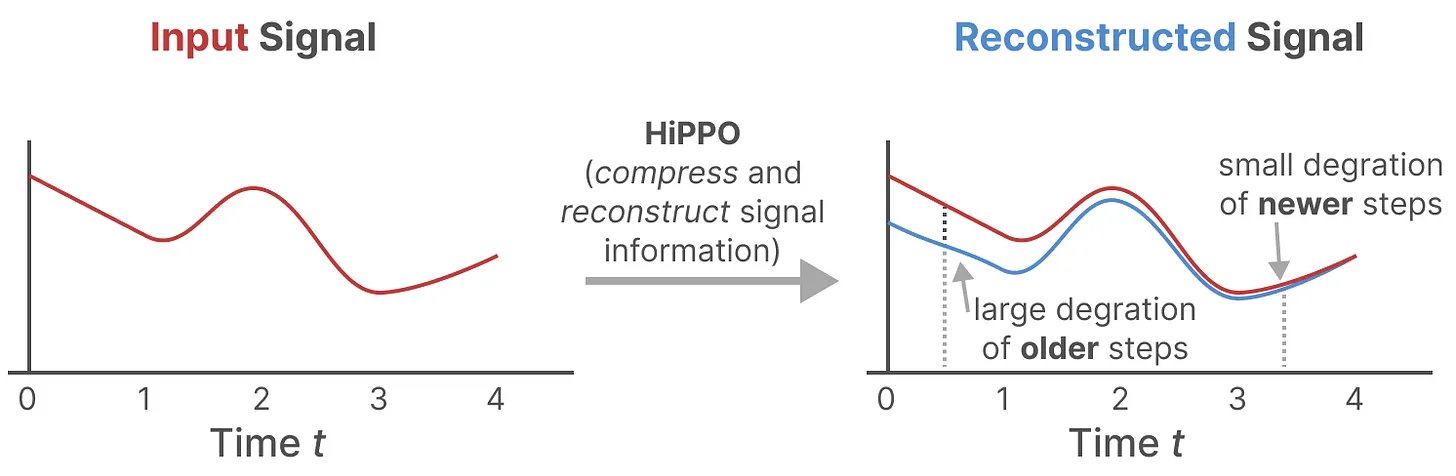
它使用矩阵构建一个“可以很好地捕获最近的token并衰减旧的token”状态表示(to build a state representation that captures recent tokens well and decays older tokens),说白了, 通过函数逼近产生状态矩阵 A 的最优解,其公式可以表示如下
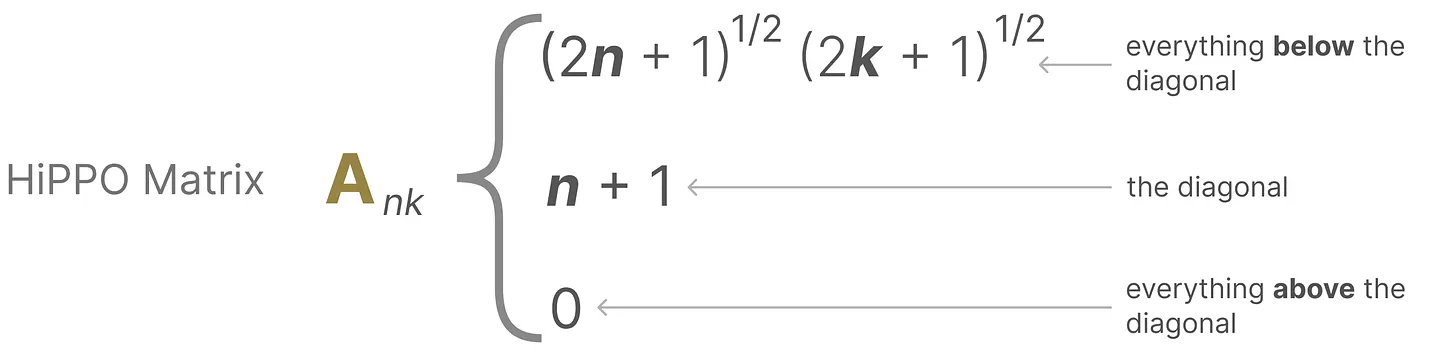
具体表示可以如下图所示
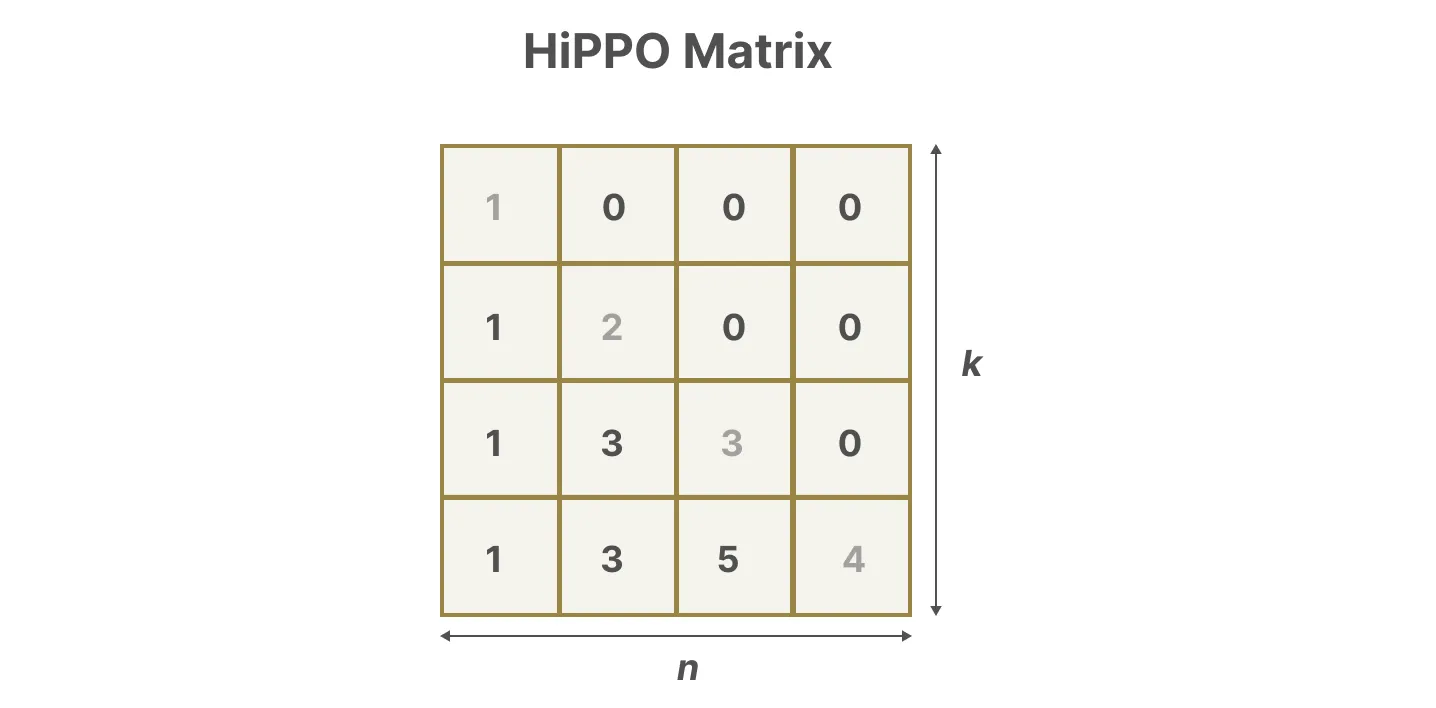
正由于HiPPO 矩阵可以产生一个隐藏状态来记住其历史(从数学上讲,它是通过跟踪Legendre polynomial的系数来实现的,这使得它能够逼近所有以前的历史),使得在被应用于循环表示和卷积表示中时,可以处理远程依赖性
如此,S4的定义就出来了:序列的结构化状态空间——Structured State Space for Sequences,一类可以有效处理长序列的 SSM(S4所对应的论文为:Efficiently Modeling Long Sequences with Structured State Spaces)
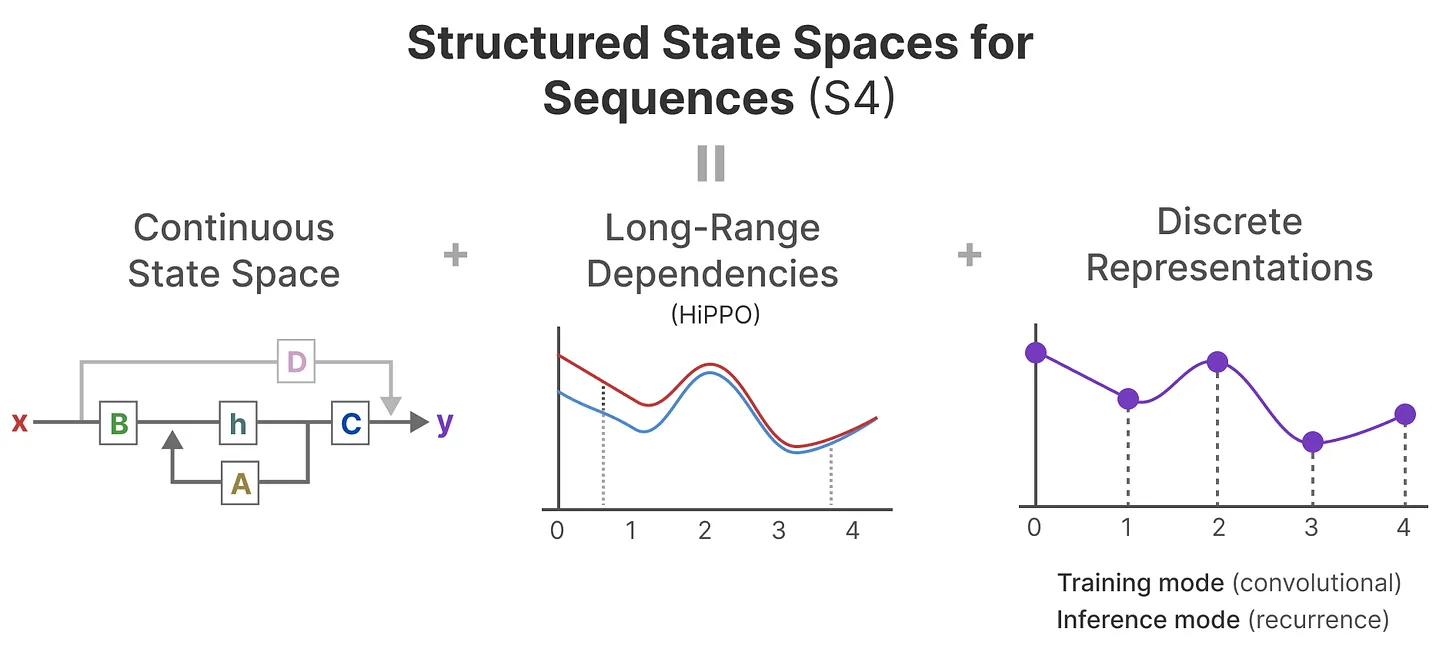
且对矩阵A 做了改进
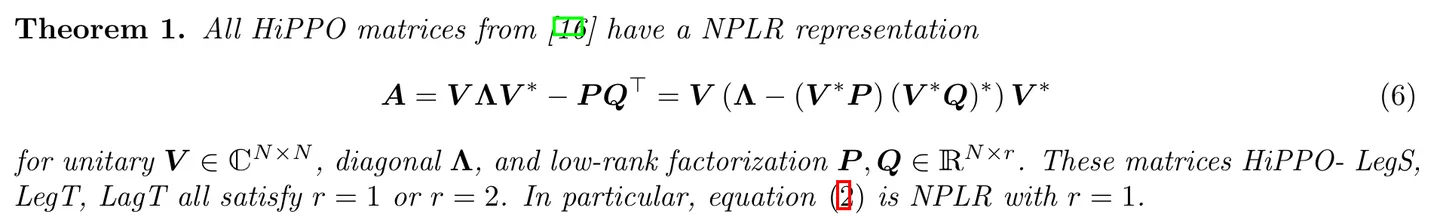
2.2(选读) Mamba一作Albert Gu举的S4的一个应用示例
注,本部分只作为选读,因为本部分要介绍的重点 上文已经介绍过了,但为何还是要增加这个选读部分呢,一者 本部分来自mamba论文的一作Albert Gu的解读,虽然其公式表达不如上文第一部分的表达顺眼(比如状态被他改写成x,输入被他改写成u),但有些论文的表达还是用的Albert Gu的这个表述,故权衡利弊,还是增加本部分
2.2.1 改进transformer不擅长处理超长的序列的问题:输入u到状态x
序列数据一般都是离散的数据 比如文本、图、DNA
- 但现实生活中还有很多连续的数据,比如音频、视频,对于音视频这种信号而言,其一个重要特点就是有极长的context window
- 而在transformer长context上往往会失败,或者注意力机制在有着超长上下文长度的任务上并不擅长(所以你才看到各种对注意力机制的改进,比如flashattention等等,即便如此一般也就32K的上下文长度,在面对100w的序列长度则无能为力),而S4擅长这类任务
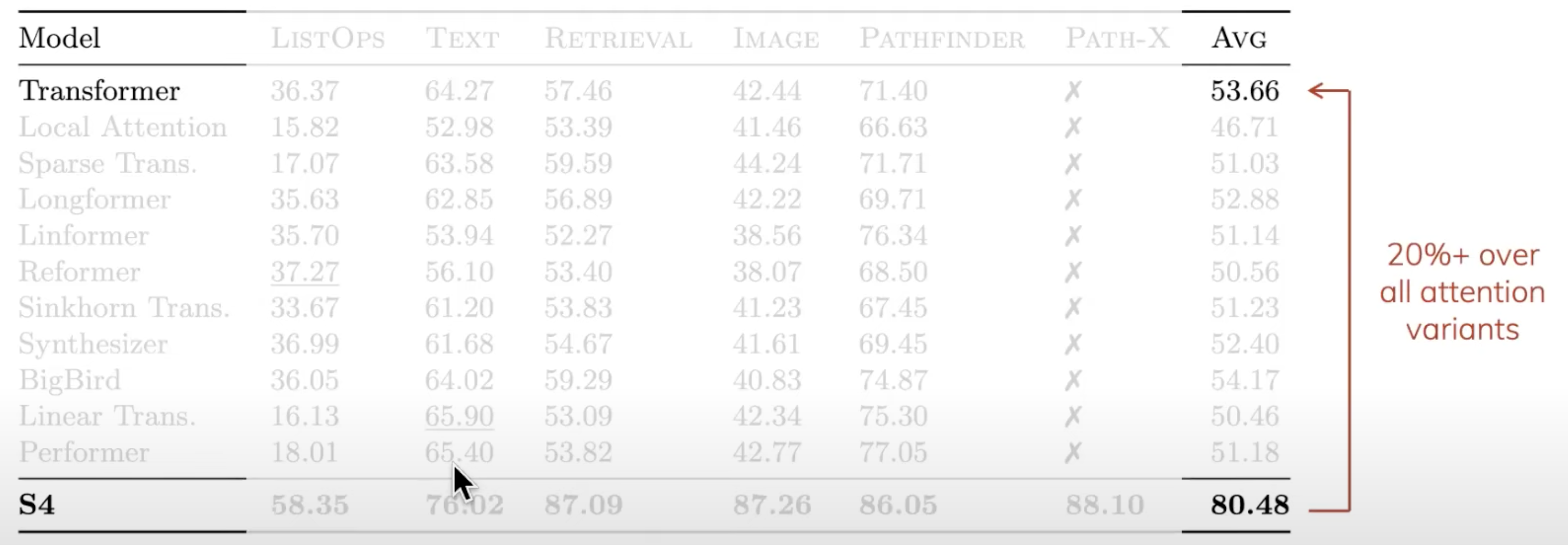
为了方便大家更好的理解,Albert Gu举了一个金融领域的例子
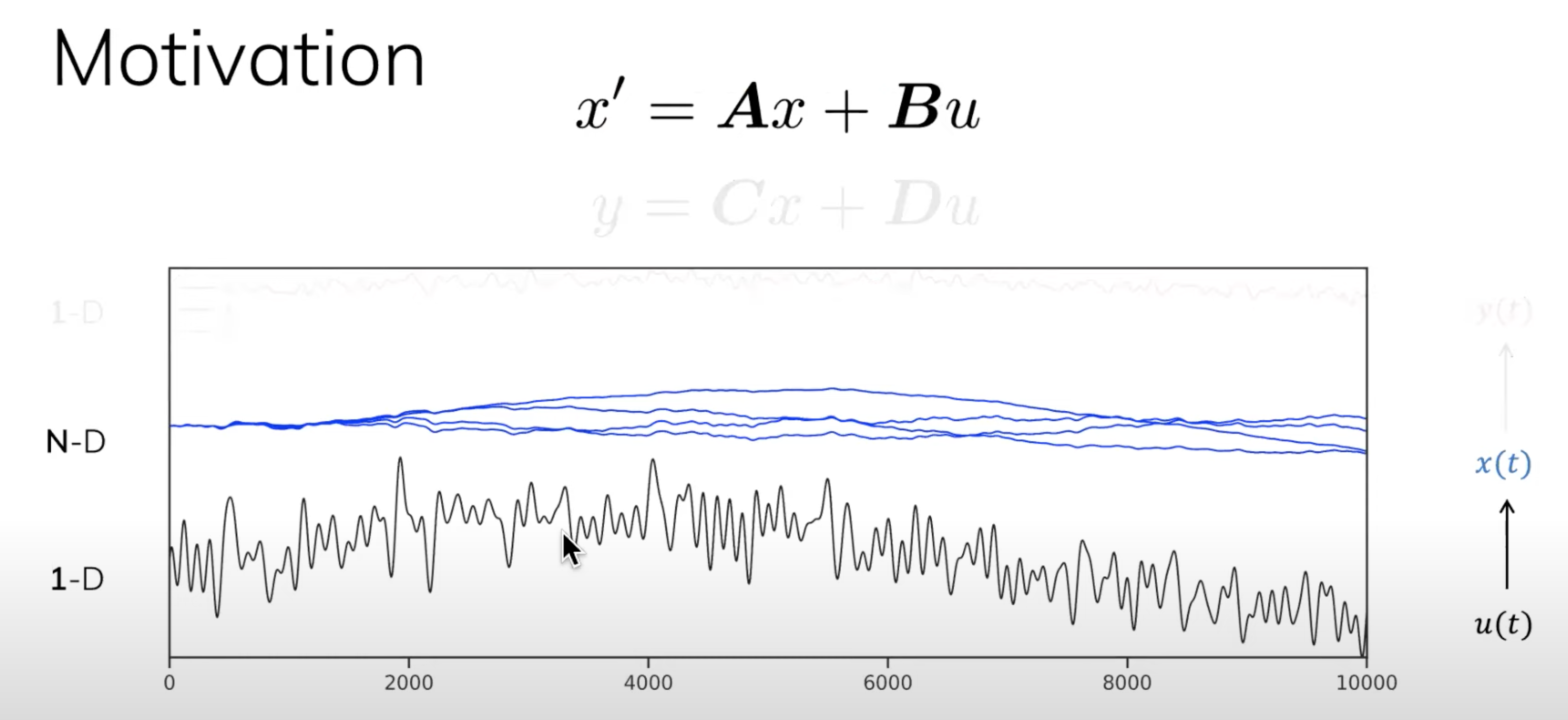
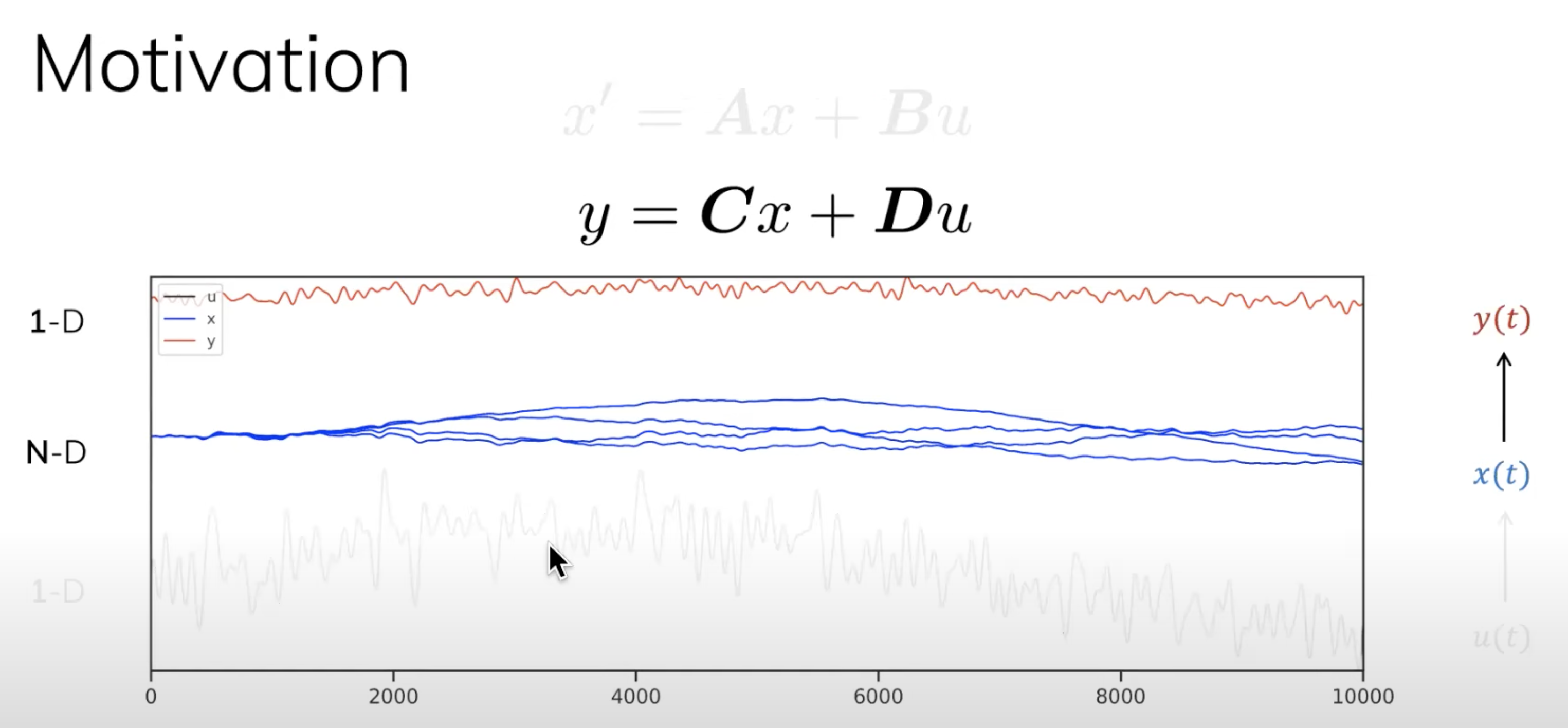
1.即根据输入,计算其EMA(如下图所示,黑色的一直在跳跃着的曲线是输入x,输出y是蓝色的线)
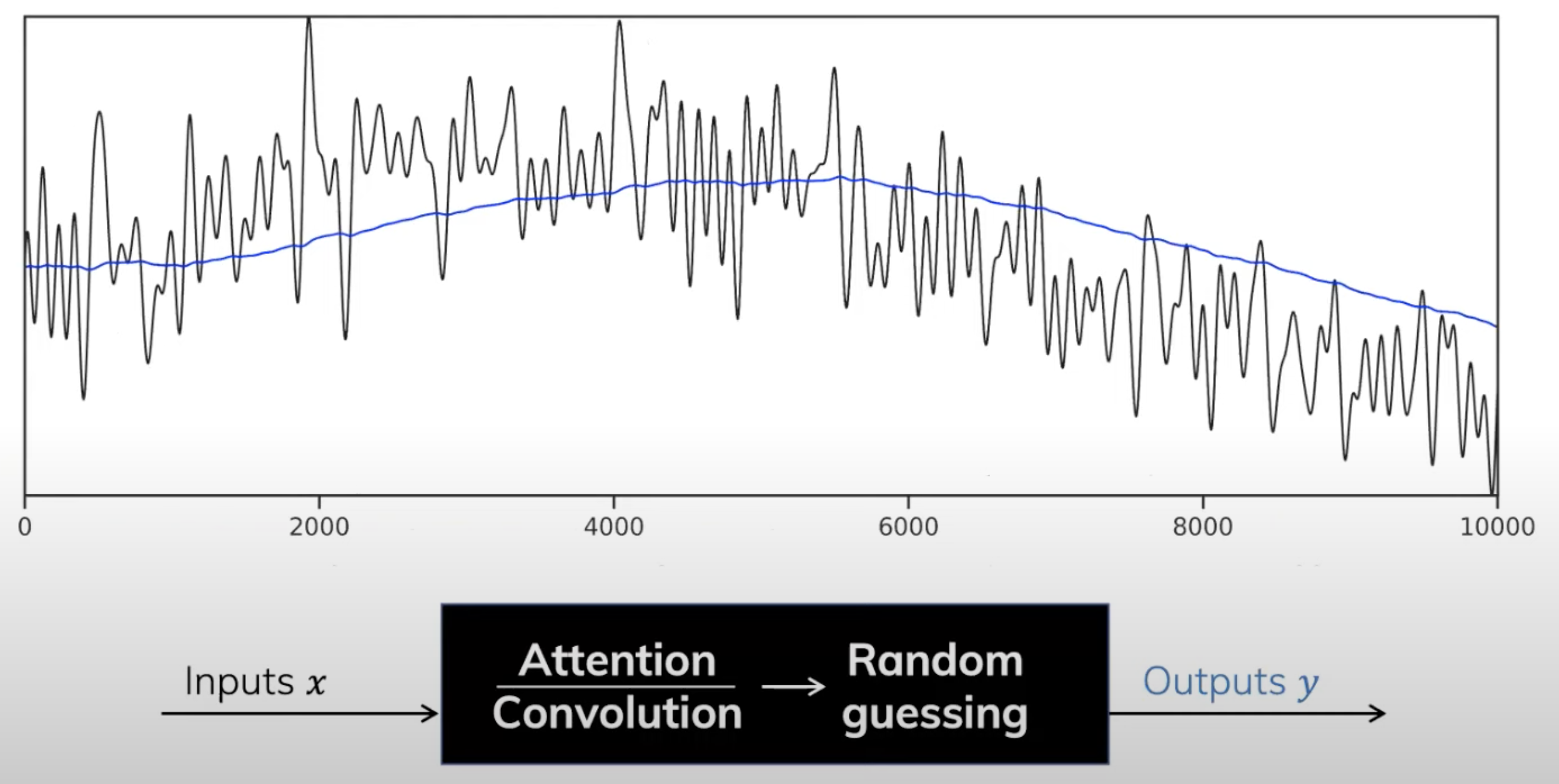
由于EMA(Exponential Decaying Measure)有着unbounded context(无限长度),Transformers和Convolution因为都只有着有限的上下文窗口而不好计算
2.Albert Gu发现EMA其实是整个signal的一个summary,相当于是过往所有信号历史的加权平均值,其权重呈指数衰减之势(下图中绿色的线即相当于投影到的指数衰减)
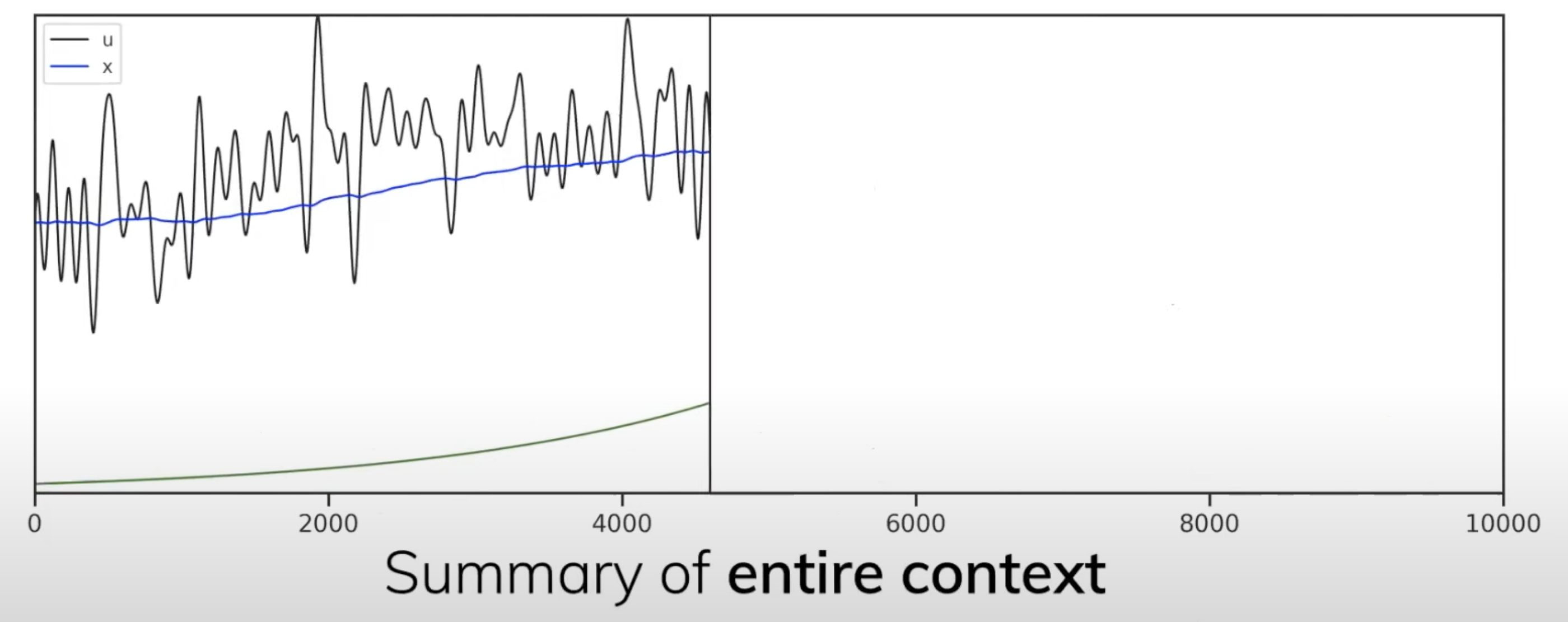
3.如果用u表示input,且表示对应的summary(可能你看到这里 觉得表示有点乱,包括很快你还会看到:输入u、状态x、输出y,其实刚好就是和上文第一部分的表述反过来了,上文第一部分是用的h(t)表示的summary,x表示原始输入)
那么该summary可以在常数时间内快速计算得到(即summary of entire context update in constant time):
![]()
这个summary作为对之前信息的一个总结,也可以认为是对“当前事物所处在一个什么样的状态”的建模,而随着新信息的不断输入,那么当前事物所处的状态也会不断更新
注:总之,相比用x 表示对应的summary,其实如果用h表示对应的summary,会更清晰,如此,也和上文的第一部分的表达统一起来了
2.2.2 HiPPO的定义与推导:state compresses the history of input
我们已经知道 RNN 被诟病的一个点恰恰是 hidden state 的记忆能力有限(毕竟hidden state 的大小是固定的, 但是需要记忆的内容是随着 sequence length 增加的,用一个有限的容器去装源源不断的水流, 自然要有溢出)
那怎么改善这个问题呢?或者怎么定义一个好的 hidden state 的记忆
假设时刻我们看到了原始输入信号
的之前部分:
1.我们希望在一个memory budget来压缩前面这一段的原始input来学习特征,一个很容易想到的方法是用多项式去近似这段input
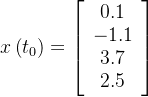
2.在我们接收到更多signal的时候,我们希望仍然在这个memory budget内对整段signal进行压缩,自然,你得更新你的多项式的各项系数(总之,注意,不管输入怎么变,这些系数一开始都不用因为输入变化而变化,甚至一开始都可以随时初始化,然后随着为了预测越发准确而对历史数据的不断更好压缩,在训练过程中调整系数的具体数值),如下图底部所示
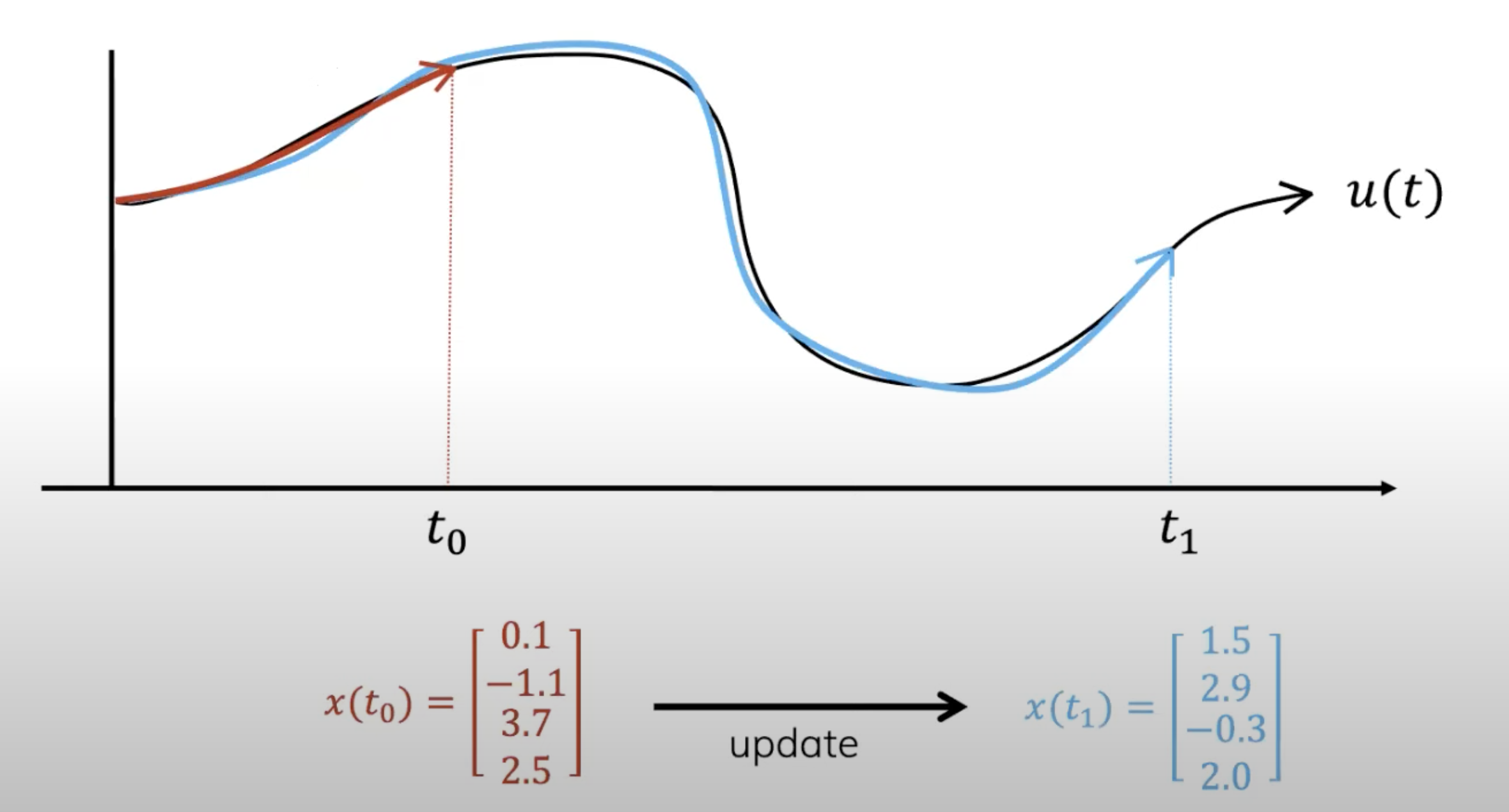
3.以上,会涌现出两个问题:
1. 如何找到这些最优的近似?
2. 如何快速地更新多项式的参数?
为了解决这两个问题,我们需要一个measure去定义一个近似的好坏程度。例如,可以使用EDM
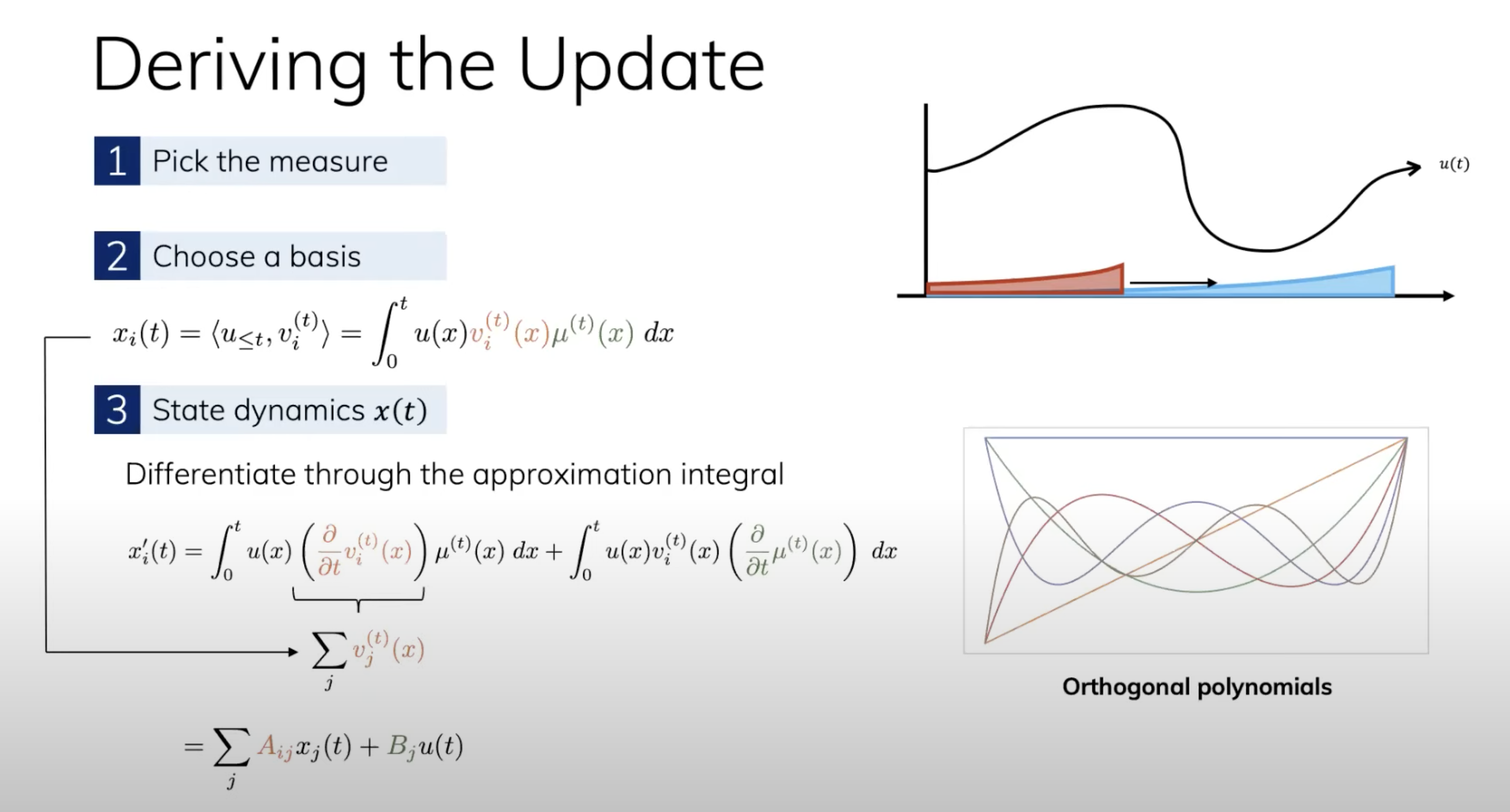
4.这就引出了HiPPO的正式定义,其为两个信号和两个矩阵的组合:
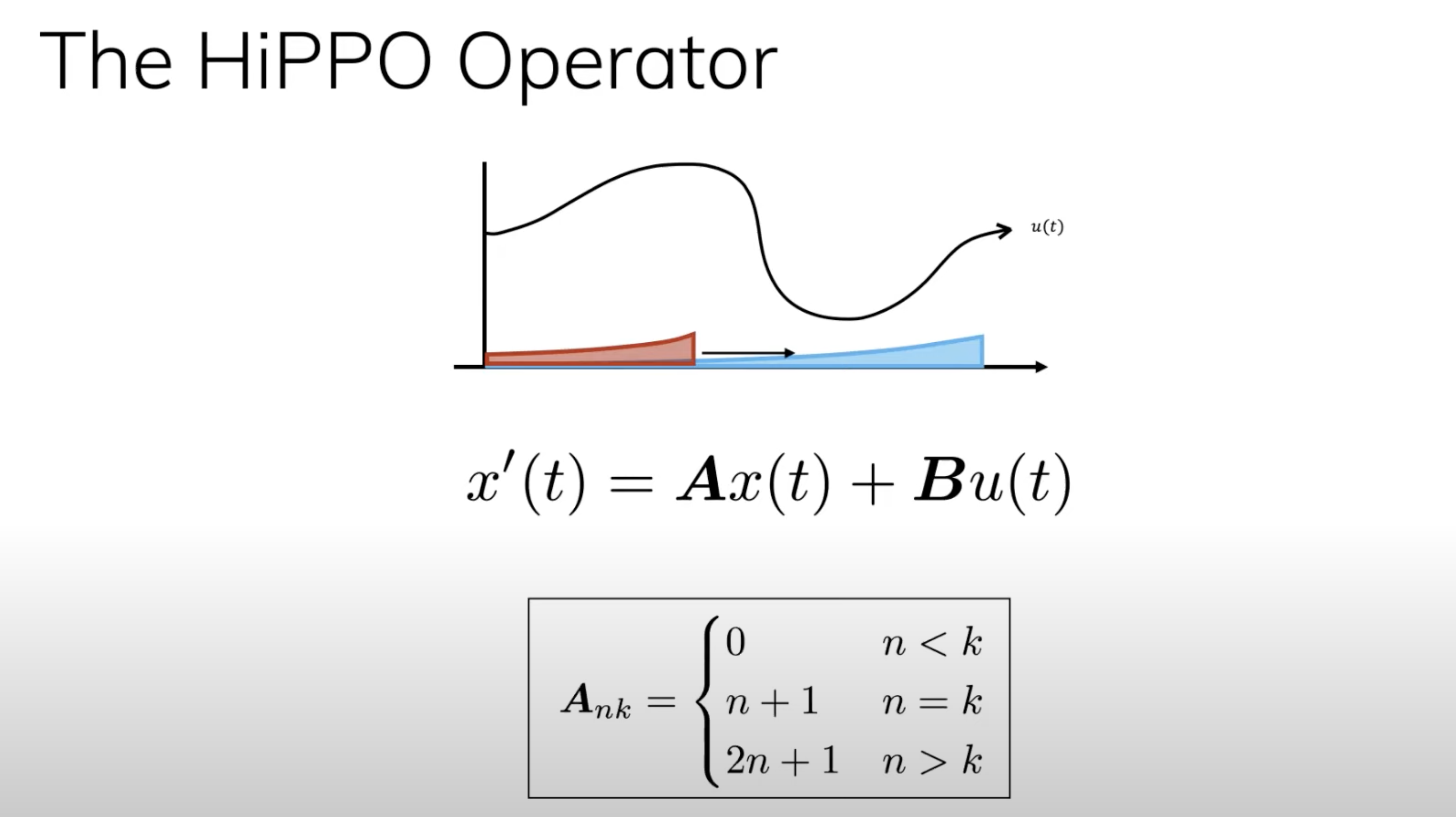
注:如果把上图的、
改由
、
表示,原始输入
改由
表示,就是上文介绍过的下图这个表达式。
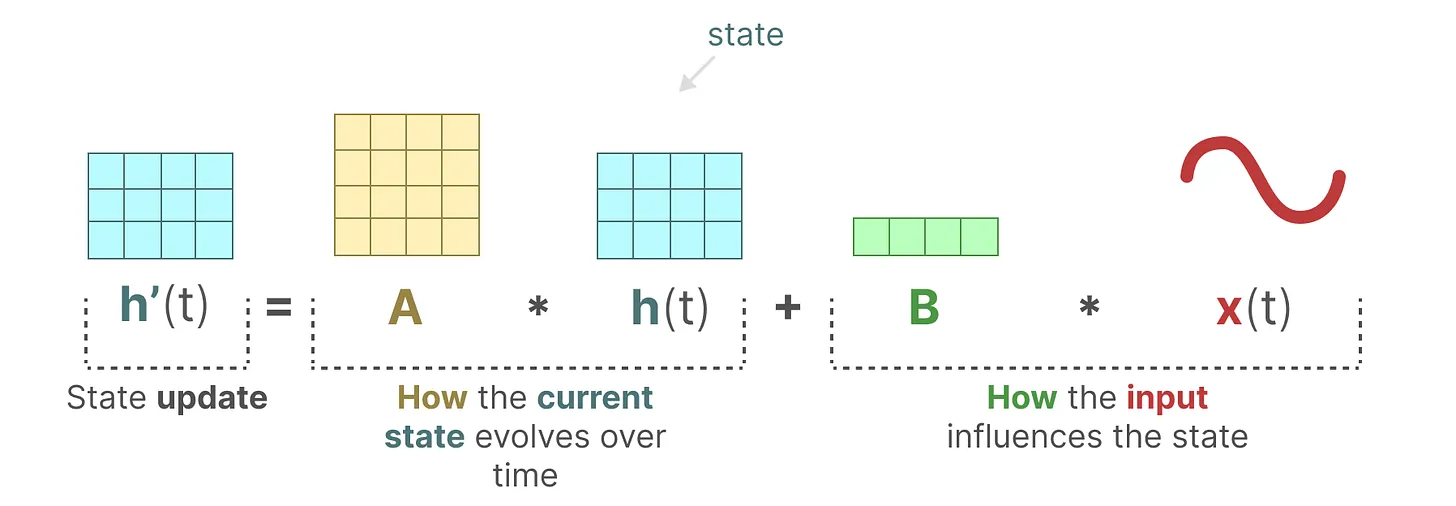
而这个矩阵A就是HiPPO矩阵,比如可以是这样:

5.HiPPO相当于将函数映射到函数,这里给个通俗的例子解释一下,如下图所示,这里的是原始输入信号,
是压缩后的信号(对应上文第一部分的状态hidden state
)
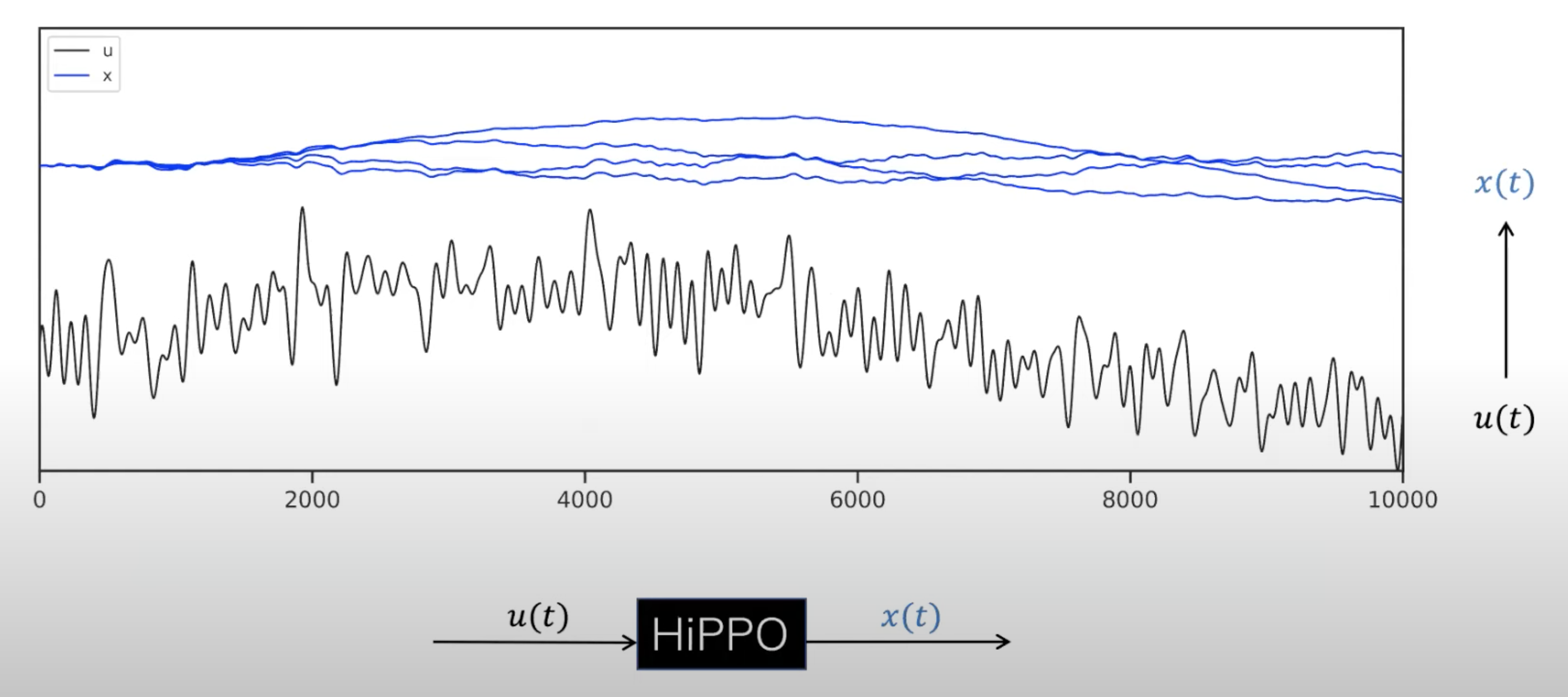
现给定一个持续增长的,HiPPO允许online update压缩的
,如下图所示
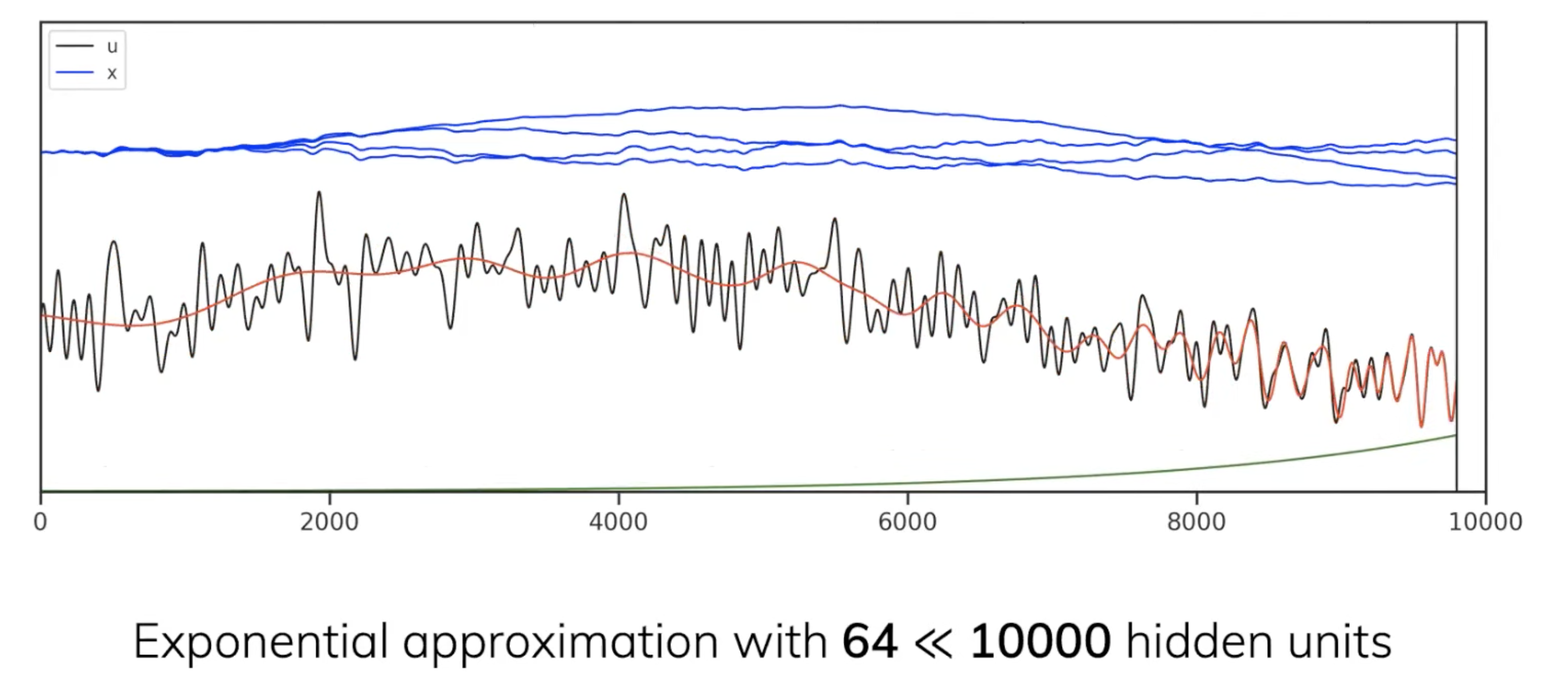
如果一条序列的长度为10000(横轴 sequence length=10000),则代表有1万个1维的数字,那想完全表示这个序列,则需要10000unit
很明显不现实,我们考虑使用一个64unit的polynomial压缩器(相当于64个不同的hidden state,即N=64,对应矩阵的大小为
,当然 下图为了画图方便只画了4个),去表示10000unit(相当于拿 一个 64 维的向量 去记 一万个1 维的数字),所以是非常高度的压缩
最终,发现EDM很不错,保留了大量之前的信息,其中红色的线相当于对输入的重建(可以看出来,离当下最近时刻的 其刻画最准确,至于离当下最远的时刻 则其刻画的不那么准确 )
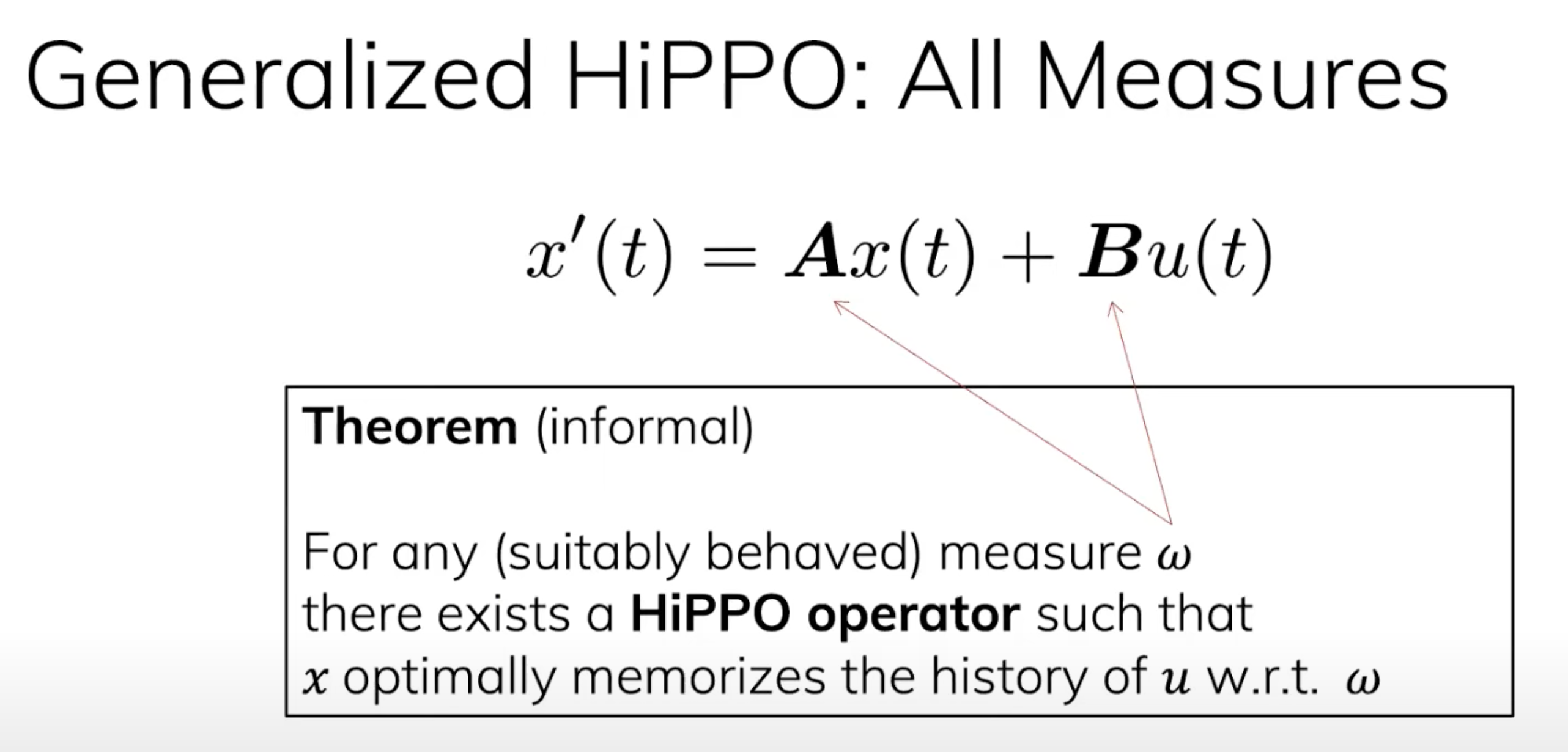
6.上面都是用EDM这个measure的,但是我们在学习过程中用的往往不只一个measure(例如一个time-varying measure can change over time),这个时候如何去建模?
最终,作者得到了一个结论:HiPPO可以在各种measure上面成立
2.2.3 HiPPO的高阶化(输入u到状态x最后输出y)
发现HiPPO在低阶信号上work后,我们希望将它扩展到高阶信号上。阶数越高,与LLM越相似,工作的价值就越大
1.但是我们不能直接堆叠HiPPO算子,因为不断增加维度会引起维数爆炸:
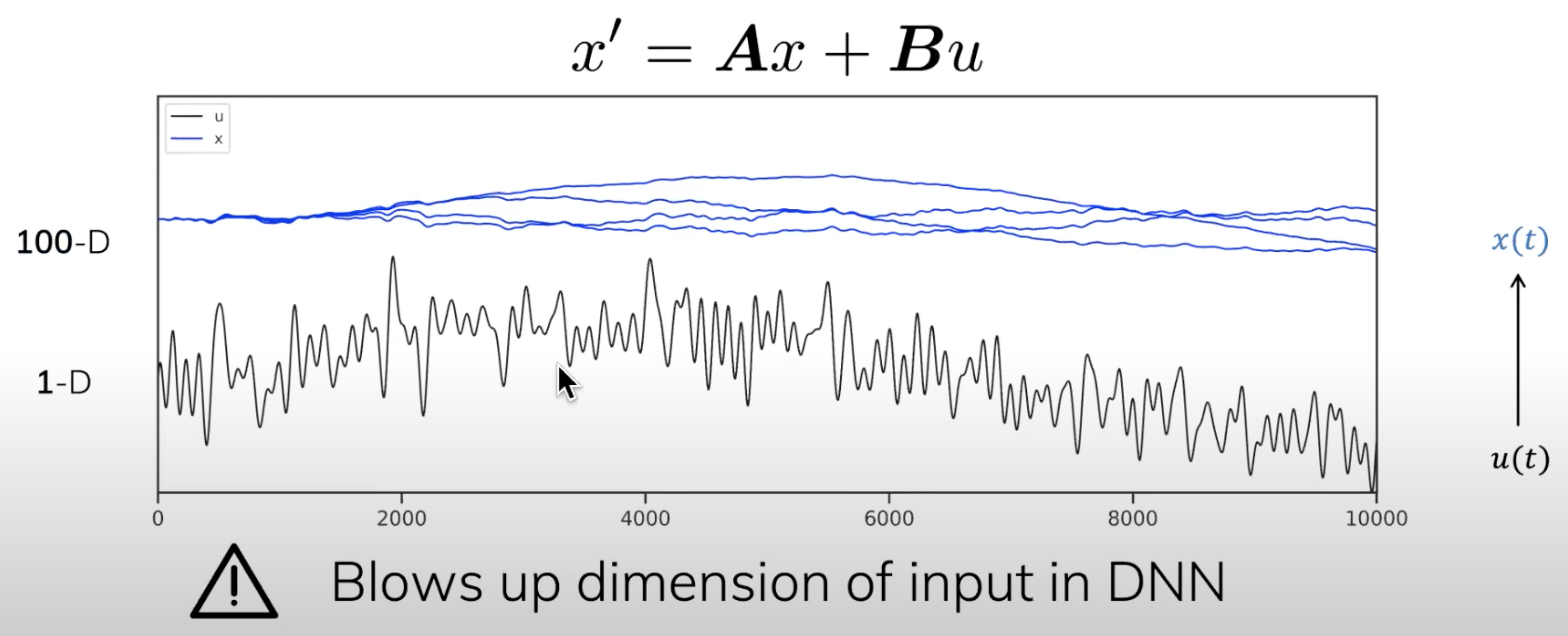
2.作者想到了非常精妙的一个方法,如下图所示,通过蓝色state 的线性组合
得到最终的输出红色
,至于
是skip connection,是绕开state
直接从input
到输出
的一个连接
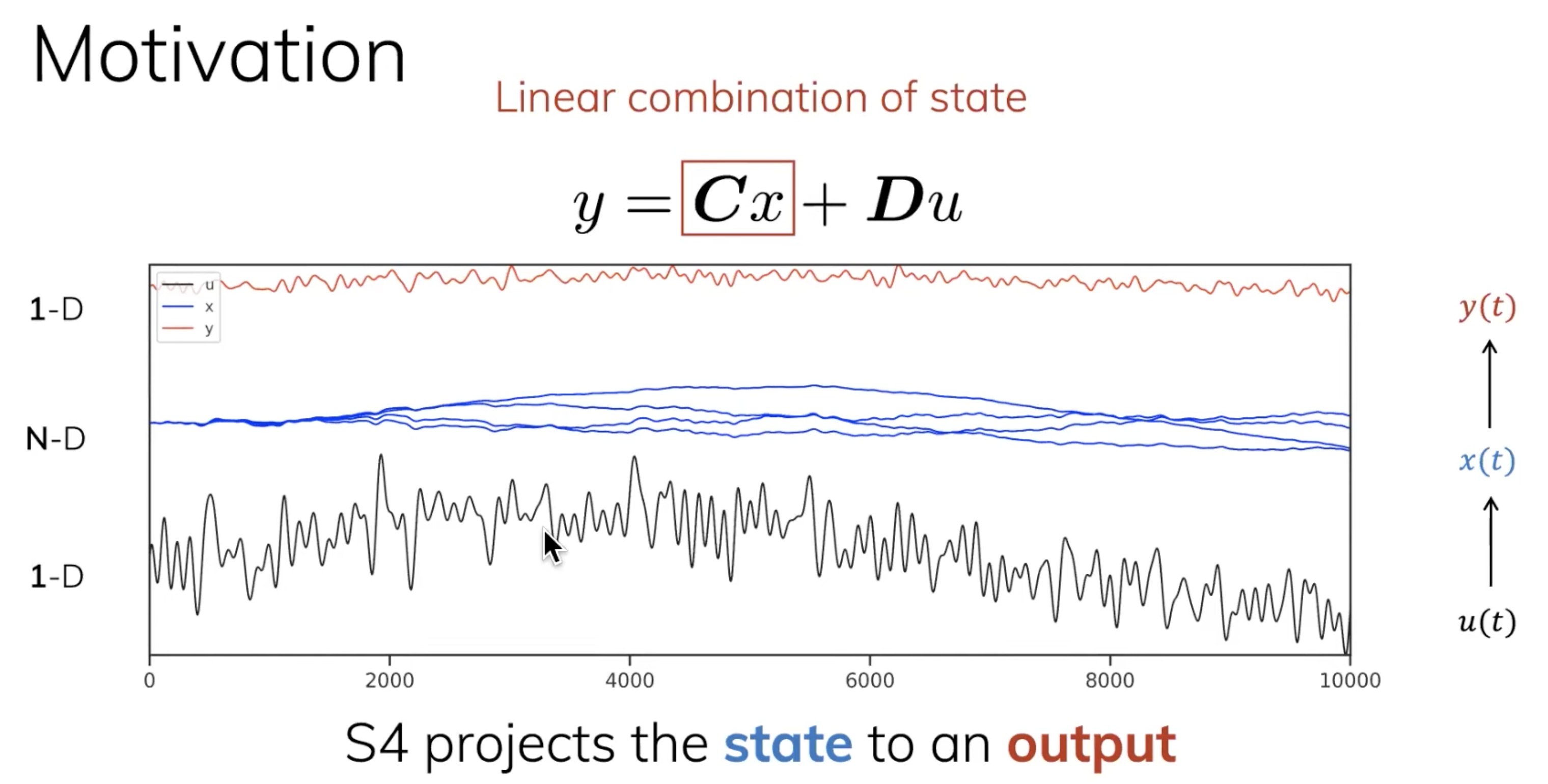
注:如果改用上文第一部分的表达,则如下图所示(state 改由
表达,input
改由
表达)
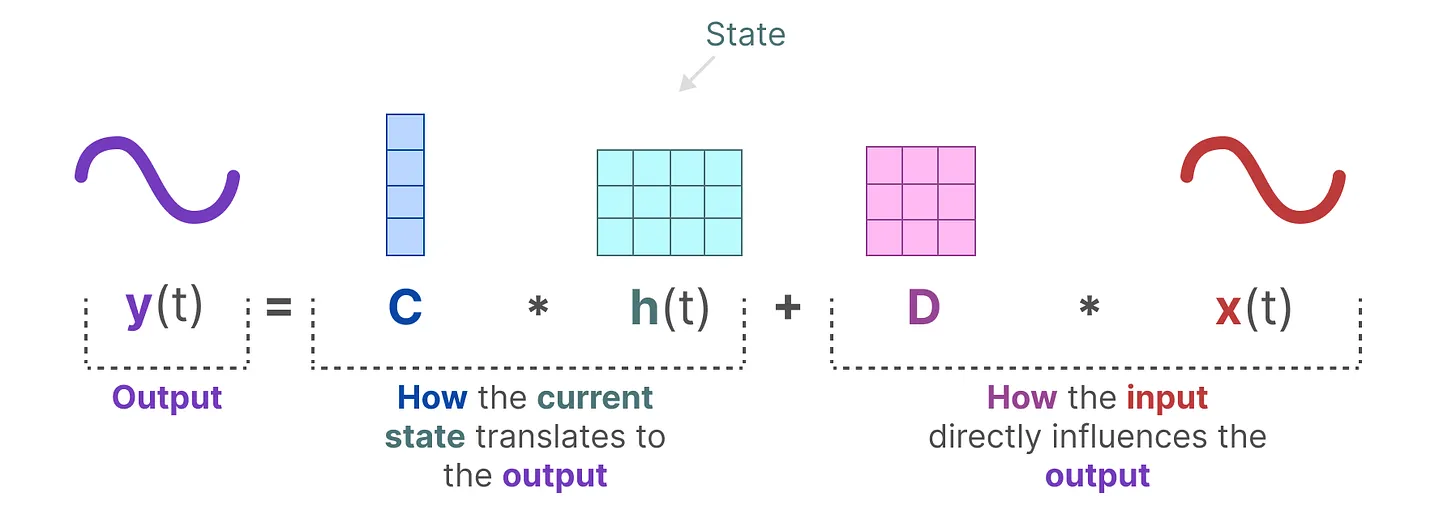
最终把这两个方程统一放到一块,便是上文第一部分所述的这个图
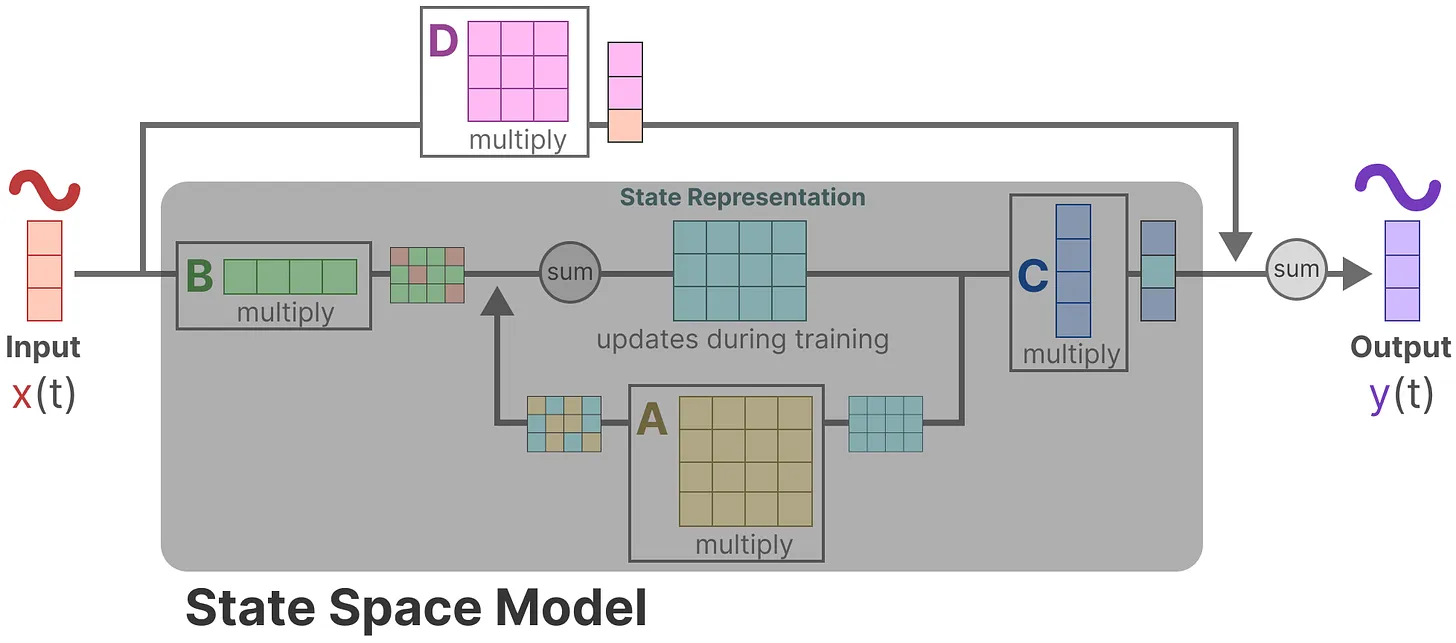
3.这样,我们通过两个方程定义S4
一个是之前定义的
(下一时刻的
) 来将input
记忆成state,如下图左侧所示
现在又定义了
来将state
线性组合成一个输出,如下图右侧所示
4.有意思的是,推出来的这些公式组成了一个1960年在ASME会议上提出的State Space Machine! SSM由Kalman提出,原文在这:A New Approach to Linear Filtering and Prediction Problems
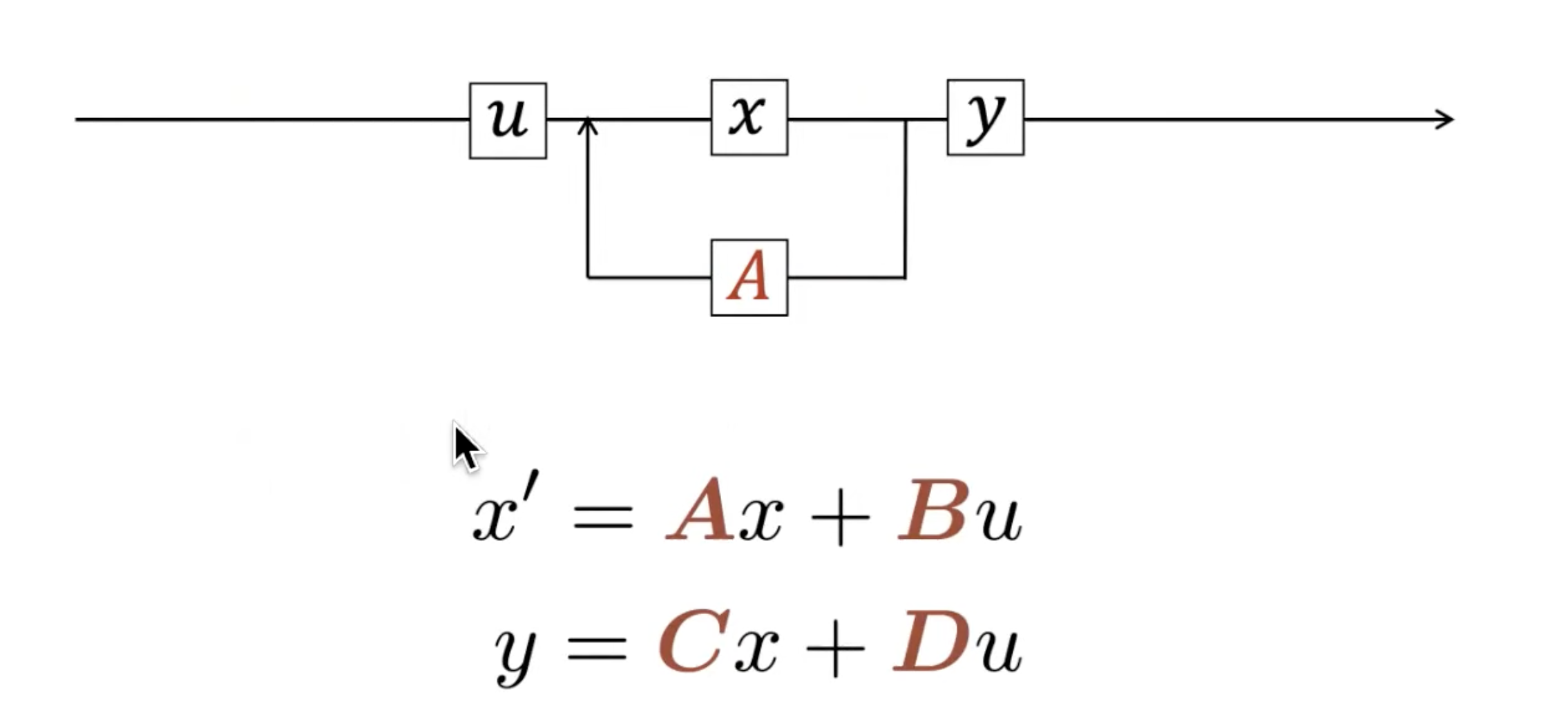
而我们关注的S4不就是基于「上图 + A B C D这4个矩阵」而发展出来的么(当然,下图是用的上文第一部分的表达)
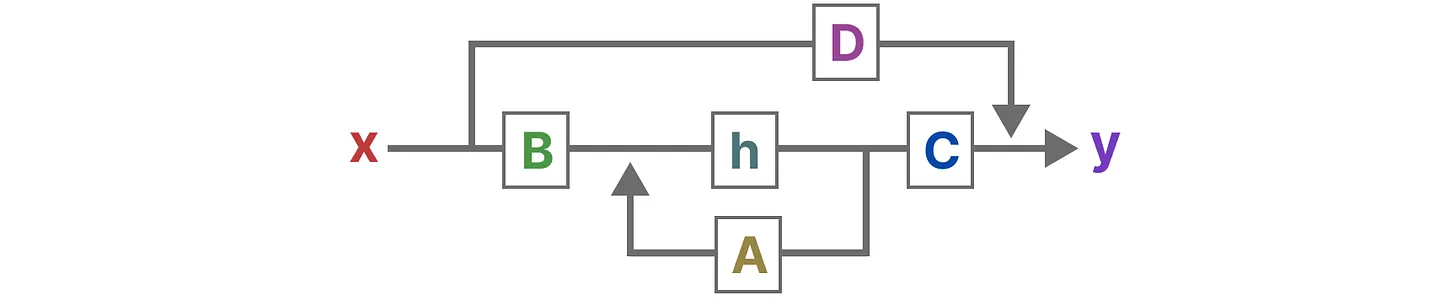
我们正式定义下S4
1.首先,有一个state space model,简称为SSM
2.其次,在下图所示的两个方程中插入特定的矩阵值

3.接着,学习对应的参数
下图所示的便是S4的三个性质
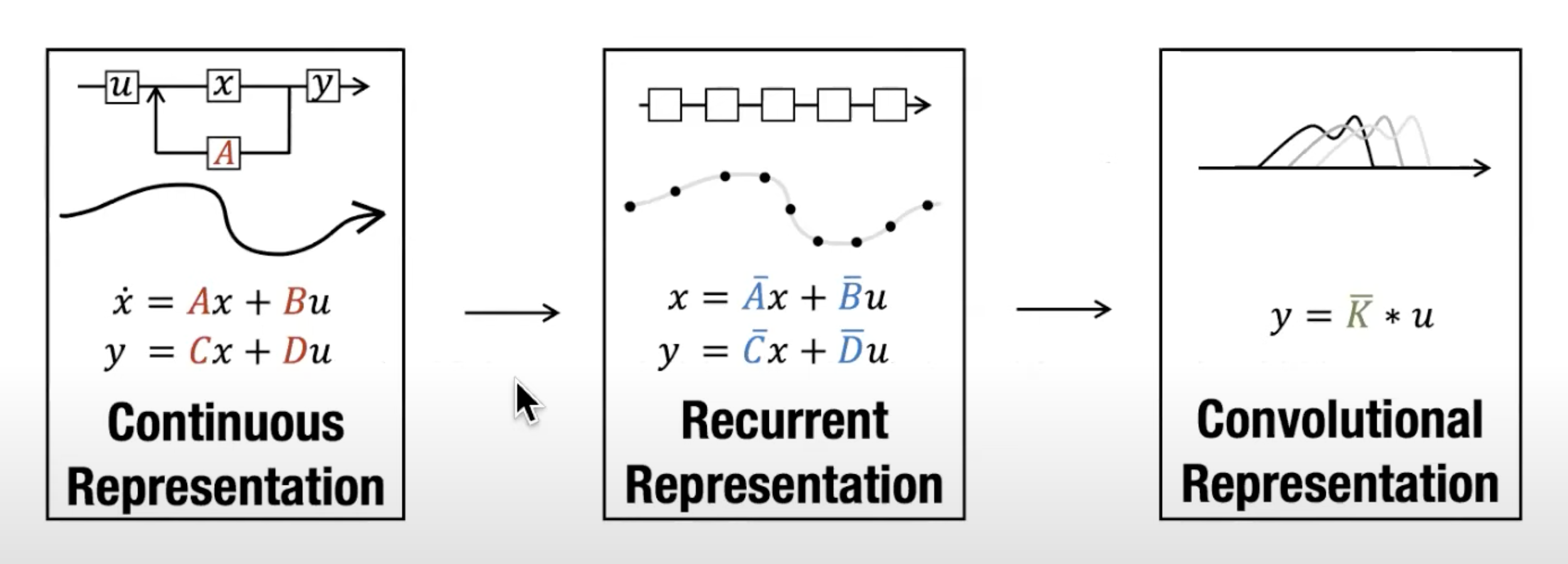
最终,状态空间模型(SSM)将这些表示作为深度学习管道中的一层(A state-space model (SSM) uses these representations as a layer in a deep learning pipeline),并且矩阵是根据数据进行学习得到的(例如 如之前所说,基于梯度优化),通常有
个这样的SSM并行存在,每个对应一个隐藏维度(具体见下文的3.1.1.2 S4中三个矩阵的维度表示、维度变化)
- 为了保留序列历史信息,在HiPPO中采用正交多项式投影历史数据,并转换成具有特殊初始化矩阵A和B的SSM形式(To preserve the sequence history, HiPPO [24] projects the history on a basis of orthogonal polynomials, which translates to having SSMs whose A, B matrices are initialized to some special matrices)
- SSM以循环方式允许高效推断(即生成):为了生成下一个时间步的输出,只需要当前时间步的状态而不是整个输入历史记录(This recurrent form of SSMs allows efficient inference (i.e., generation): to generate the output of the next time-step, one only needs the state of the current time-step, not the entire input history)
2.2.4 用Recurrent表示进行快速的infer
第二个性质是有效的online计算,这点之前在HiPPO提到了,就是计算下一时刻的state 只需要当前时刻的state
和全局输入
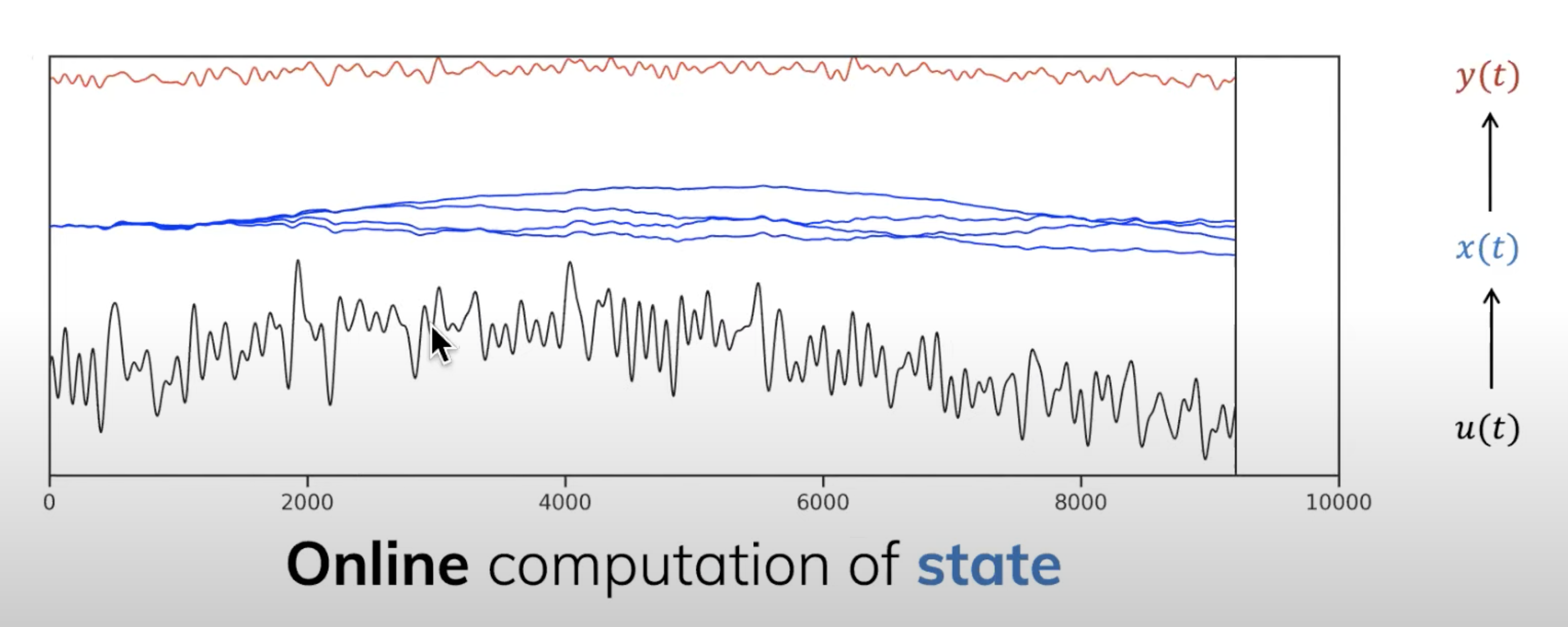
虽然需要全局输入,但是这个全局的计算是常数时间的,这与RNN相同,而与Transformer/CNN不同
之所以是常数时间,也与RNN相同,因为有state(中间这条蓝线),这导致下一个state的计算只需要当前的state + 随时间而变化的全局的输入(类似
)
2.2.5 用Convolutional表示进行快速的训练
SSM的一个问题是,当知道未来的signal的时候,训练是低效的。有没有办法并行化SSM?作者提出了使用一个卷积核 ,绕过状态
,直接从输入
到输出
(而非先输入到状态、状态再到输出)

输入怎么到输出
呢?相当于通过特定的卷积滤波器K对输入进行卷积(即you can involve the input by an exponentially decaying convolution kernel),该滤波器在上图中用绿色线表示
问题好像解决了,但SSM还是存在两个问题
1.一个是计算复杂度的问题,最终通过给SSM做结构化(比如使用HiPPO矩阵,相当于变成了S4),即structured state space can be computed faster
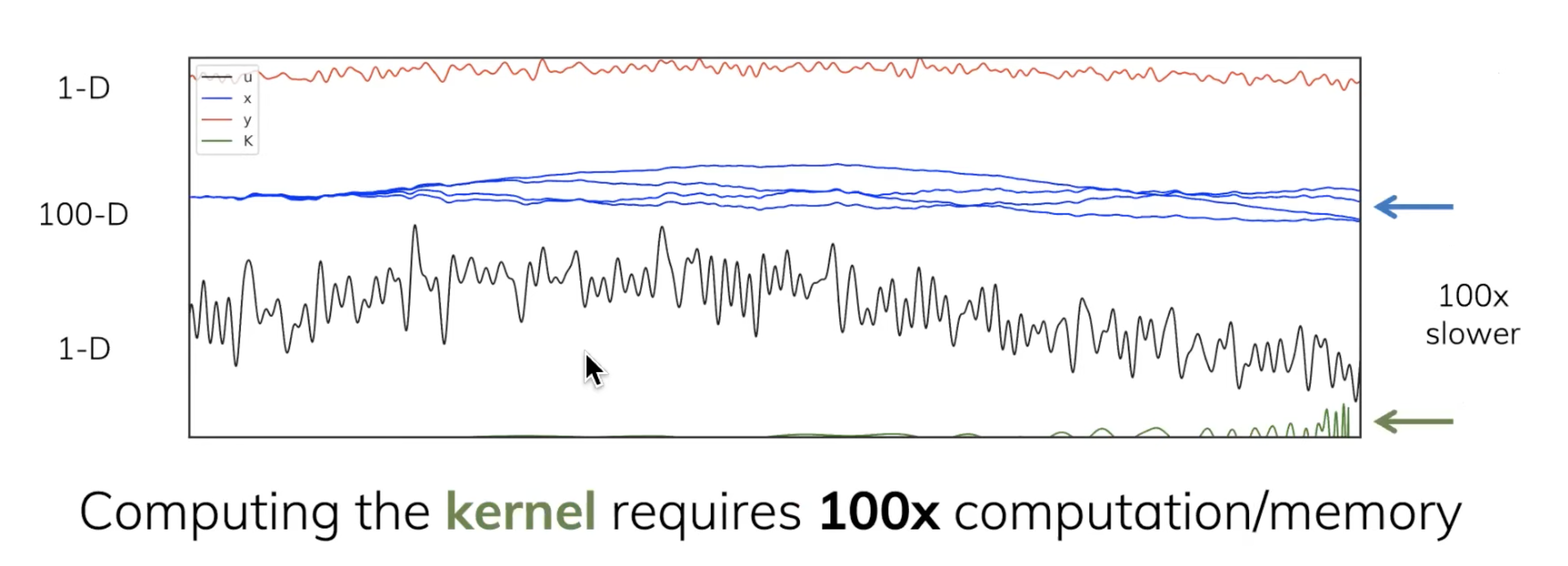
2.另一个是,作者意识到这个S4某种意义上就是一个很fancy的CNN(包括可以以不同的方式参数化卷积内核),但是context window有时是无限长的
而刚好convolutional kernel可以无限长(至于单纯的CNN则是有限长的窗口),那其如何设计以适应有时无限长的context window呢?如下图所示

2.3 SSM的问题:矩阵不随输入不同而变化,无法针对输入做针对性推理
2.3.1 Linear Time Invariance规定 SSM中的A、B、C不因输入不同而不同
首先,Linear Time Invariance(LTI)规定 SSM中的A、B、C不随输入不同而不同。这意味着
- 对于 SSM 生成的每个token,矩阵A 、B、C都是相同的(regardless of what sequence you give the SSM, the values of A,B,and C remain the same. We have a static representation that is not content-aware)
- 使得SSM无法针对输入做针对性的推理「since it treats each token equally as a result of the fixed A, B, and C matrices. This is a problem as we want the SSM to reason about the input (prompt)」
此外,如下图所示,无论输入x 是什么,矩阵 B都保持完全相同,因此与x无关
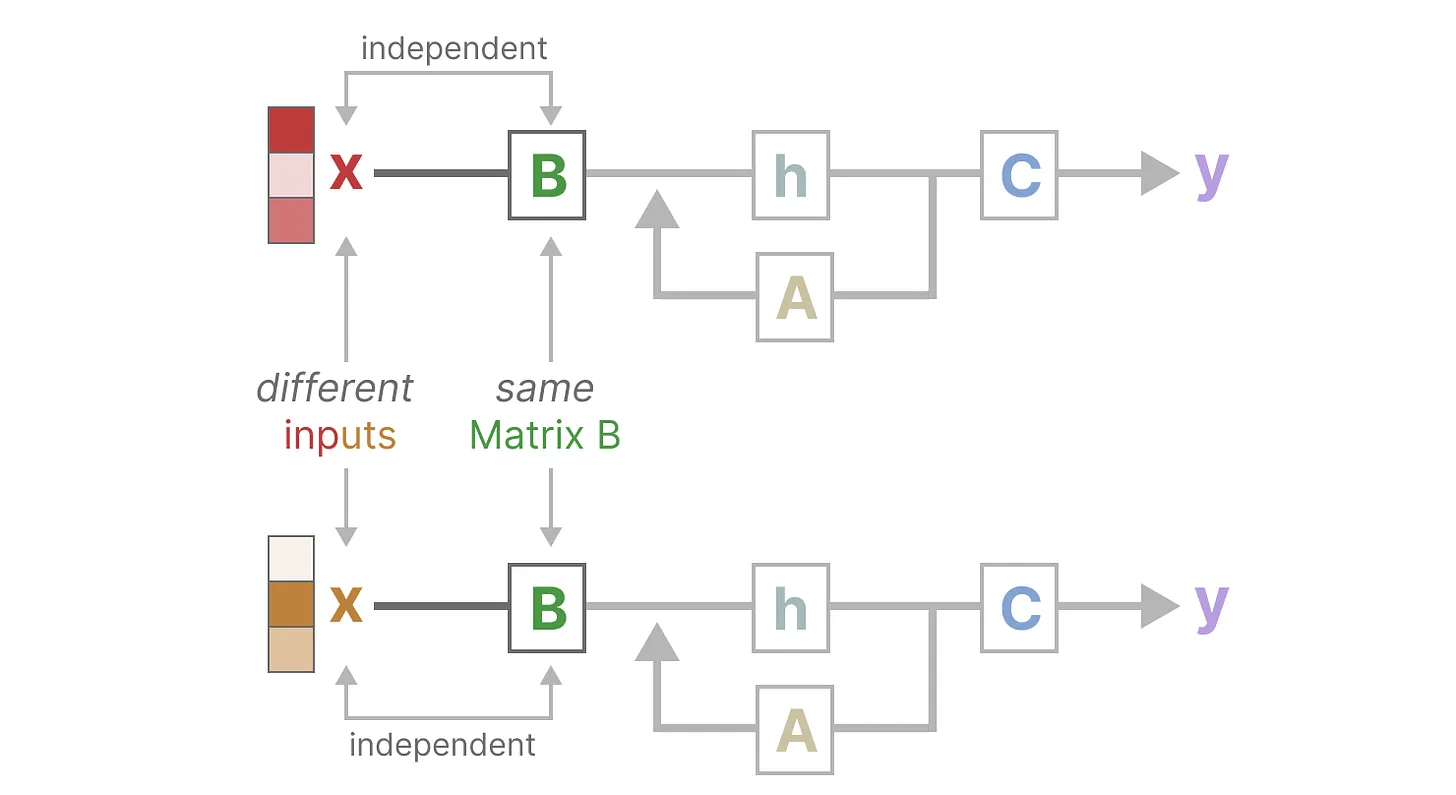
同样,无论输入如何,A和C也保持固定
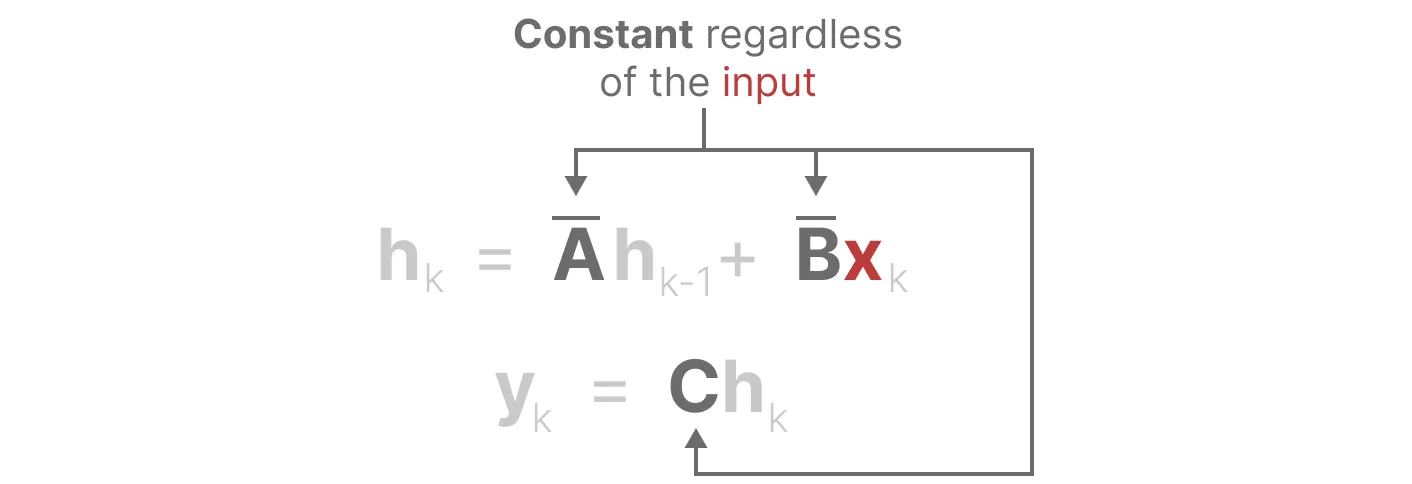
注意,可能有的文章不会给你强调,但从负责任且清晰明确的角度上还是要重点说下
即这里的不变性特指不随输入变化而变化,但是输入确定之后,在训练过程中,矩阵是可以根据需要去做梯度下降而变化的
2.3.2 如何改进S4以根据各个token重要性程度的不同而选择性聚焦的示例
比如 “I want to order a hamburger.”这句
- 如果没有选择性,S4会花费相同的“精力”来处理每个单词:
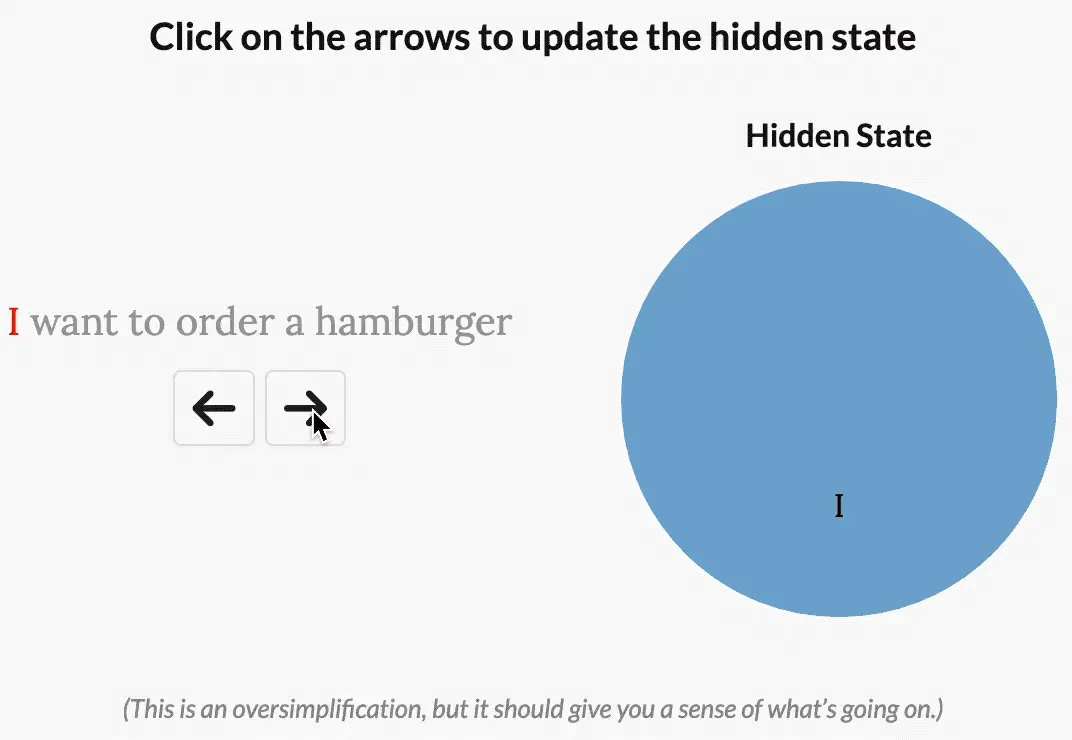
- 但如果是一个试图对这句话的意图进行分类的模型,它可能会想更多地“关注”order、hamburger,而不是want、to
如下图所示,而通过使模型参数成为输入的函数,模型就可以做到“专注于”输入中对于当前任务更重要的部分,而这正是mamba的创新点之一
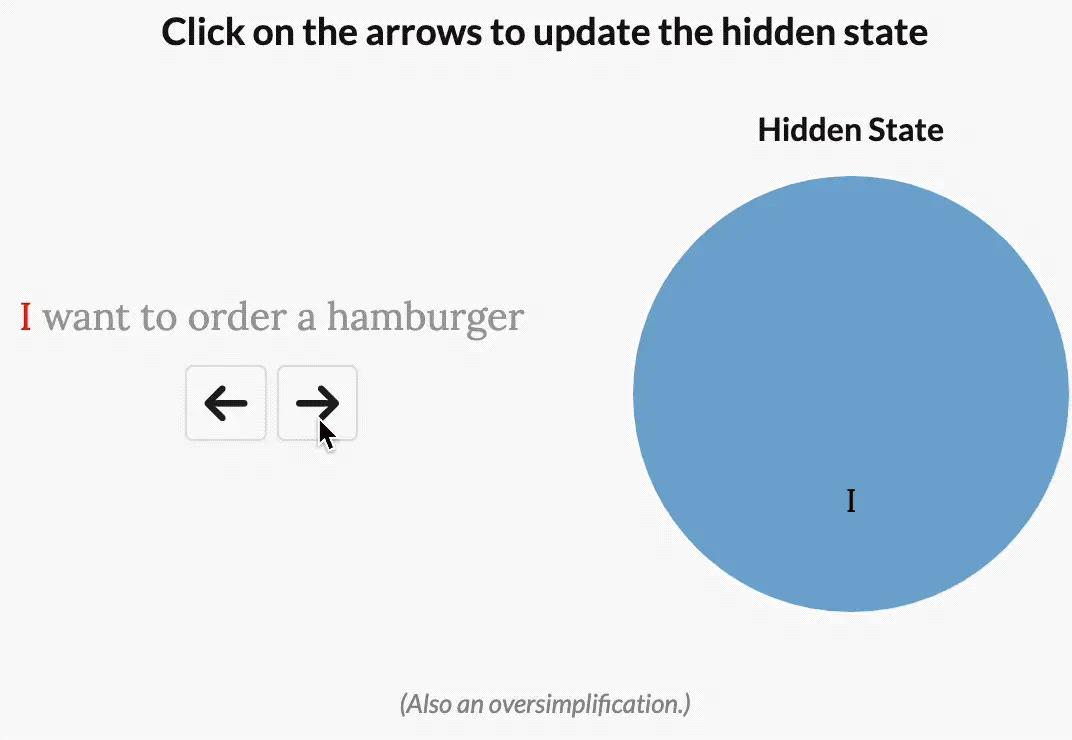
凡事也有利有弊,虽然mamba可以“专注于”输入中对于当前任务更重要的部分,但坏处是没法再通过CNN做并行训练了,原因在于:
1.让我们回想一下之前计算的卷积核
![]()
在S4中,我们可以预先计算该内核、保存,并将其与输入相乘,因为离散参数、
、
是恒定的(In S4, we could pre compute this kernel, save it, and multiply it with the input . And this was fine, because
、
、
were constant)
2.但在Mamba中,这些矩阵会根据输入而变化!因此,我们无法预计算,也无法使用CNN模式来训练我们的模型(But again, in Mamba, these matrices change depending on the input! As a result, we can’t precompute , and we can’t use CNN mode to train our model)
从而下面这个式子用不上了

说白了,如果我们想要选择性,得用RNN模式进行训练(If we want selectivity, we’ll need to train with RNN mode),然偏偏RNN的训练速度非常慢,emmm,所以我们需要找到一种无需卷积的并行训练方式(详见下文的3.1.2节)
3. Mamba的三大创新
mamba(其对应论文为:Mamba: Linear-Time Sequence Modeling with Selective State Spaces,这是其对应的GitHub代码地址),在语言、音频、DNA序列模态上都实现SOTA,在最受关注的语言任务上,Mamba-3B超越同等规模的Transformer,与两倍大的Transformer匹敌,并且相关代码、预训练模型checkpoint都已开源
简言之,Mamba是一种状态空间模型(SSM),建立在更现代的适用于深度学习的结构化SSM (简称S6)基础上,与经典架构RNN有相似之处
3.1 Mamba = 有选择处理信息 + 硬件感知算法 + 更简单的SSM架构
与先前的研究相比,Mamba主要有三点创新:
1.对输入信息有选择性处理(Selection Mechanism)
2.硬件感知的算法(Hardware-aware Algorithm)
该算法采用“并行扫描算法”而非“卷积”来进行模型的循环计算(使得不用CNN也能并行训练),但为了减少GPU内存层次结构中不同级别之间的IO访问,它没有具体化扩展状态
当然,这点也是受到了S5(Simplified State Space Layers for Sequence Modeling)的启发
3.更简单的架构
将SSM架构的设计与transformer的MLP块合并为一个块(combining the design of prior SSM architectures with the MLP block of Transformers into a single block),来简化过去的深度序列模型架构,从而得到一个包含selective state space的架构设计
3.1.1 选择性状态空间模型:从S4到S6
作者认为,序列建模的一个基础问题是把上下文压缩成更小的状态(We argue that a fundamental problem of sequence modeling is compressing context into a smaller state),从这个角度来看
- transformer的注意力机制虽然有效果但效率不算很高,毕竟其需要显式地存储整个上下文(storing the entire context,也就是KV缓存),直接导致训练和推理消耗算力大。好比,Transformer就像人类每写一个字之前,都把前面的所有字+输入都复习一遍,所以写的慢
- RNN的推理和训练效率高,但性能容易受到对上下文压缩程度的限制(On the other hand, recurrent models are efficient because they have a finite state, implying constant-time inference and linear-time training. However, their effectiveness is limited by how well this state has compressed the context.)。好比,RNN每次只参考前面固定的字数(仔细体会这句话:When generating the output, the RNN only needs to consider the previous hidden state and current input. It prevents recalculating all previous hidden states which is what a Transformer would do),写的快是快,但容易忘掉更前面的内容
- 而SSM的问题在于其中的矩阵A B C不随输入不同而不同,即无法针对不同的输入针对性的推理,详见上文的2.4节
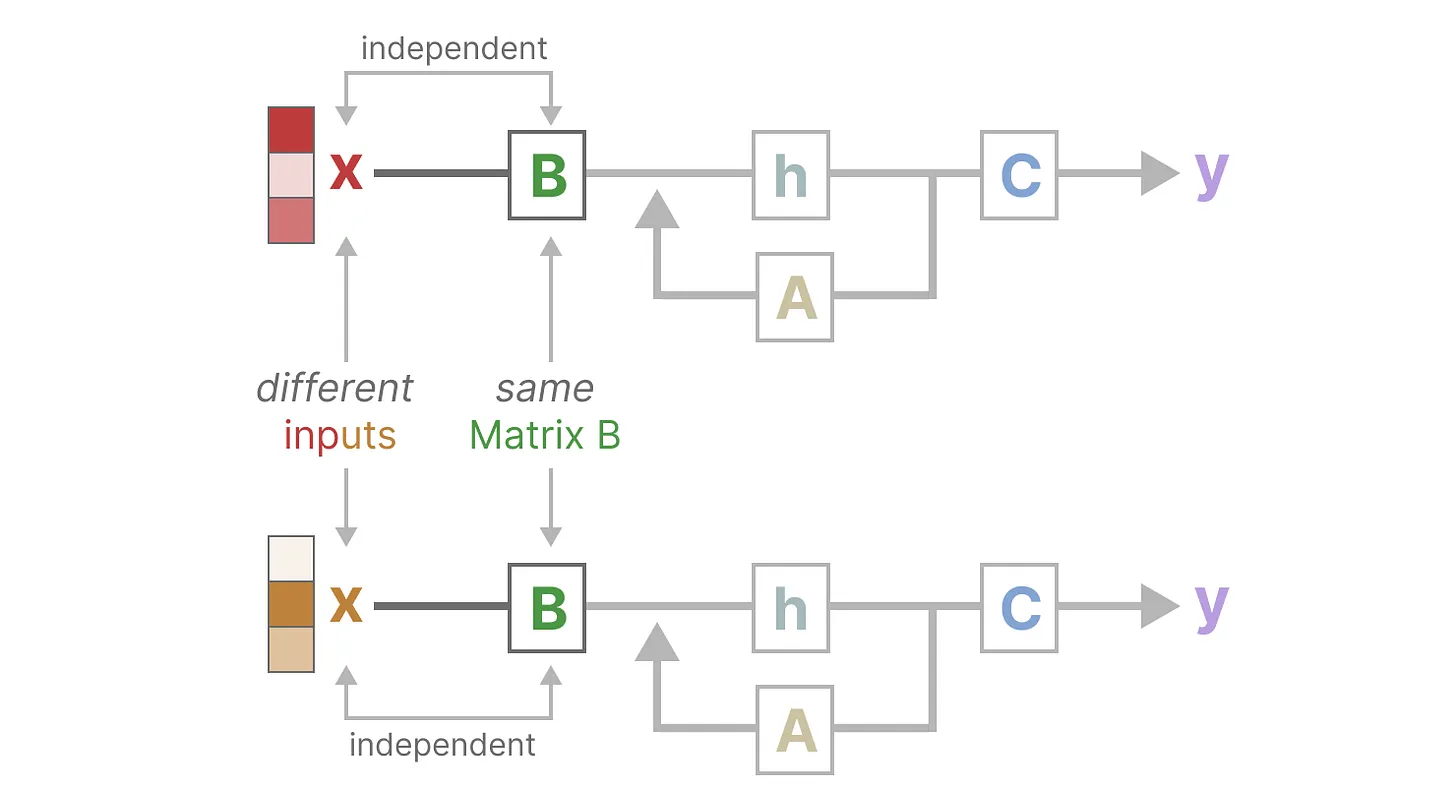
- 最终,Mamba的解决办法是,相比SSM压缩所有历史记录,mamba设计了一个简单的选择机制,通过“参数化SSM的输入”,让模型对信息有选择性处理,以便关注或忽略特定的输入。这样一来,模型能够过滤掉与问题无关的信息,并且可以长期记住与问题相关的信息。好比,Mamba每次参考前面所有内容的一个概括,越往后写对前面内容概括得越狠,丢掉细节、保留大意
为方便大家对比,我再用如下表格总结下各个模型的核心特点
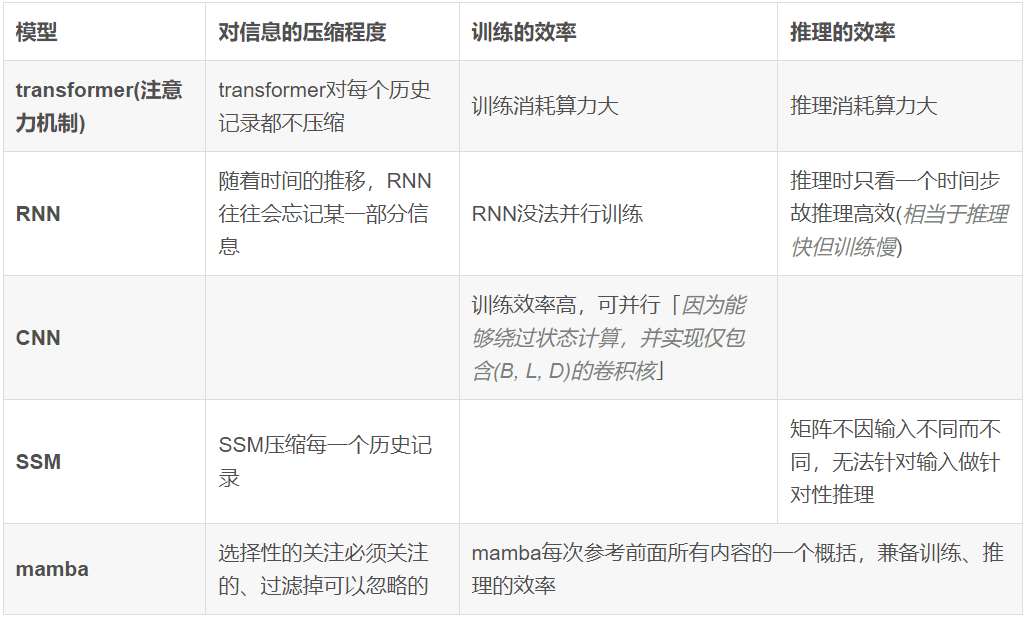
总之,序列模型的效率与效果的权衡点在于它们对状态的压缩程度:
- 高效的模型必须有一个小的状态(比如RNN或S4)
- 而有效的模型必须有一个包含来自上下文的所有必要信息的状态(比如transformer)
而mamba为了兼顾效率和效果,选择性的关注必须关注的、过滤掉可以忽略的
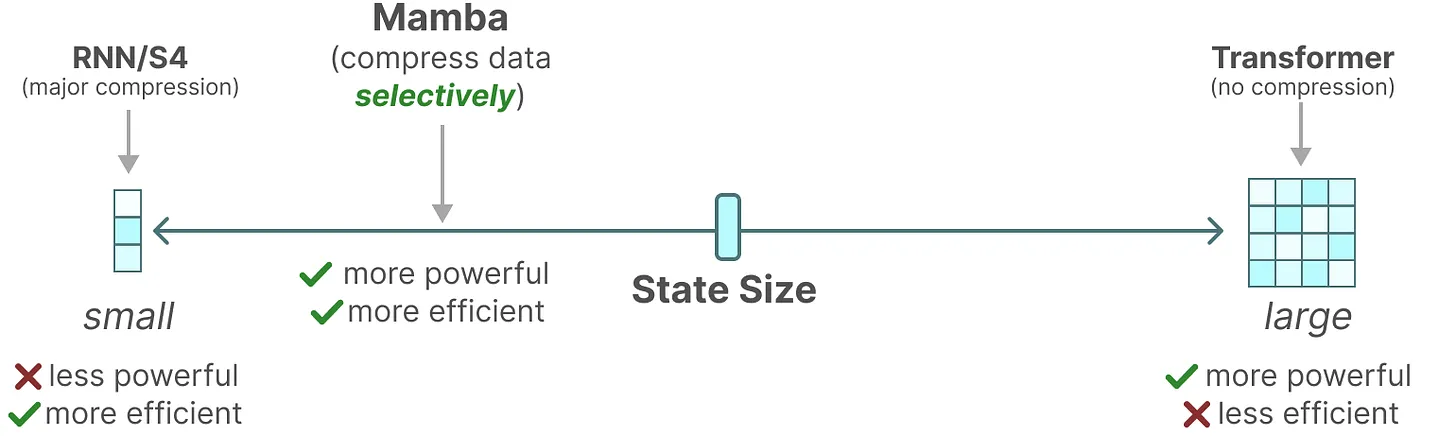
为方便大家理解,再进一步阐述mamba与其前身结构化空间模型S4的优势
3.1.1.1 mamba前身S4的4个参数的不随输入不同而不同
首先,在其前身S4中,其有4个参数(∆, A, B, C)
且它们不随输入变化(即与输入无关),这些参数控制了以下两个阶段
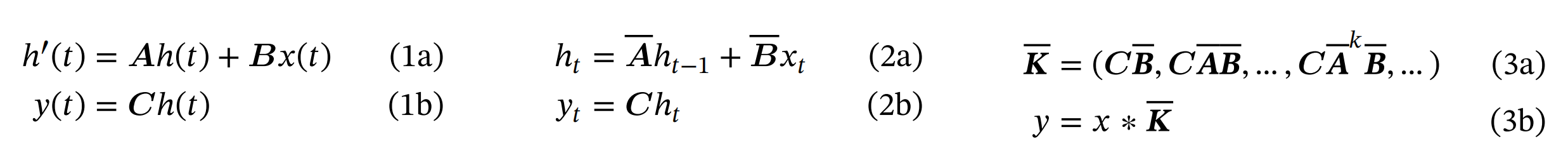
第一阶段(1a 1b),通常采用固定公式和
,将“连续参数”
转化为“离散参数”
,其中
称为离散化规则,且可以使用多种规则来实现这一转换
The first stage transforms the “continuous parameters” (∆, A, B) to “discrete parameters” (A, B) through fixed formulas A =
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。