归并排序详解（思想及C++代码实现）_c++归并排序

小伙伴们大家好，今天我们简单介绍一下归并排序。

【归并排序】类似于快速排序（快排），时间复杂度为O(nlogn)，是一种高效的排序算法，应用场景十分广阔。

归并排序的主要思想是分治和递归。

主要操作是划分和合并（同时进行排序）

【分治】字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

下面我们以一个简单的例子介绍归并排序的原理。

假设有一组数 1，5，4，8，7，我们要对其进行排序。

我们对其进行划分和合并（同时进行排序）的操作，图示如下：

注意：红色标注表示的是最小划分（即区间长度为1，无法继续划分的情况，否则以二分的方式继续划分）

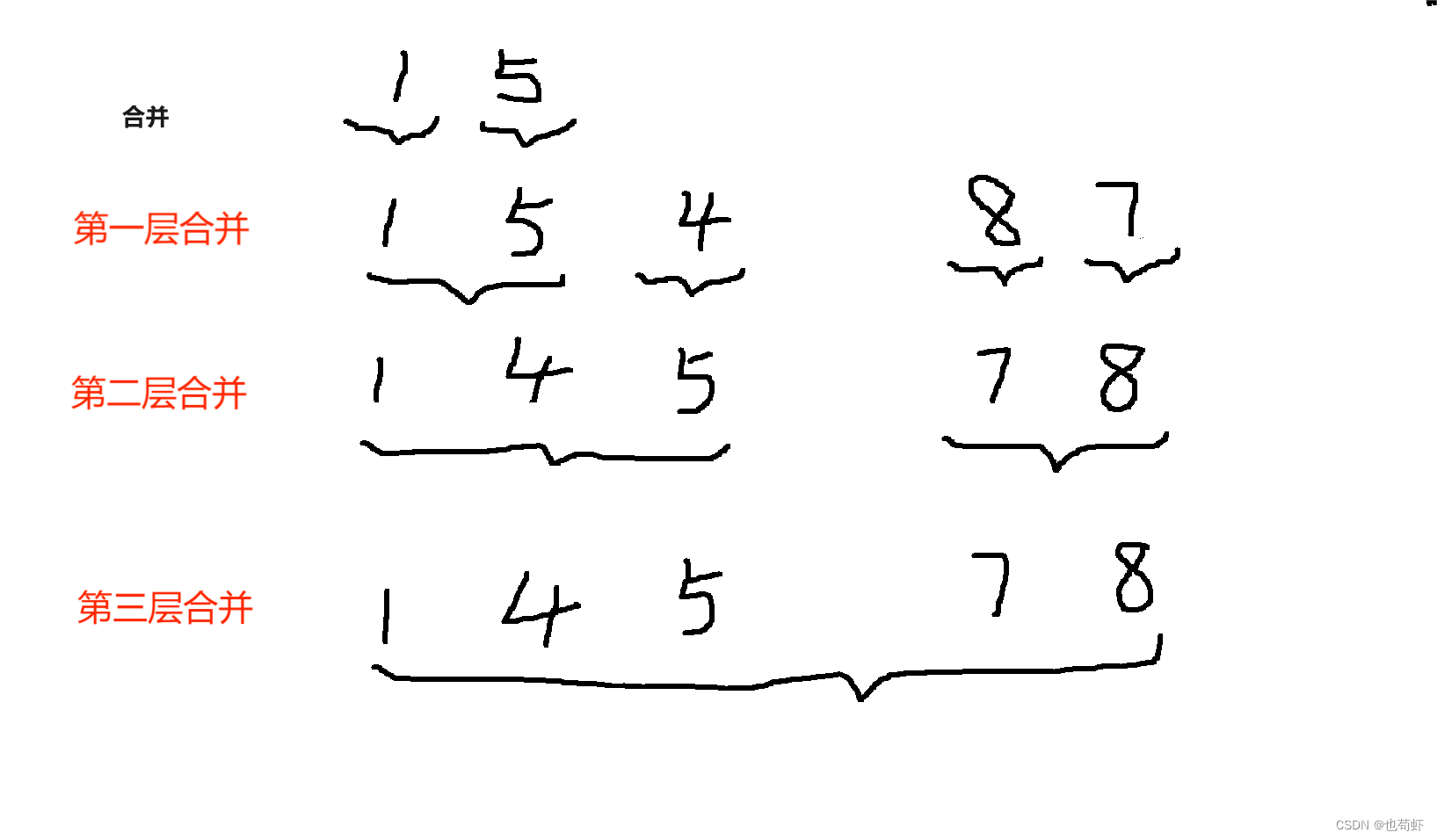
有了上面对归并排序的理解，编写代码就不难了。

关于具体操作，代码上有详细注释，我就不在这赘述了。

C++代码如下：

#include <iostream>
using namespace std;
const int N = 5e5 + 10;
int a[N], t[N], n;//t[]是辅助数组，暂存局部排序的结果
void mergesort(int s,int d)//下标 s到d 进行归并排序
{
	if (s == d)return;//如果区间长度为1，停止划分
	//否则以二分的方式继续划分
	int mid = (s + d) / 2;
	mergesort(s, mid);//递归划分左半区
	mergesort(mid+1, d);//递归划分右半区
	int i = s, j = mid+1, k = s;
	while (i <= mid && j <= d)//排序
	{
		//局部排序结果暂存到t[]中
		if (a[i] <= a[j])t[k++] = a[i++];
		else t[k++] = a[j++];
	}
	//将剩余部分接入
	while (i <= mid)t[k++] = a[i++];
	while (j <= d)t[k++] = a[j++];
	//数组赋回
	for (int g = s;g <= d;g++)
		a[g] = t[g];
}
int main()
{
	cin >> n;
	for (int i = 1;i <= n;i++)
		cin >> a[i];
	mergesort(1, n);//将数组下标 1到n 进行归并排序
	for (int i = 1;i <= n;i++)
		cout << a[i] << ' ';
	cout << endl;
	system("pause");
	return 0;
}

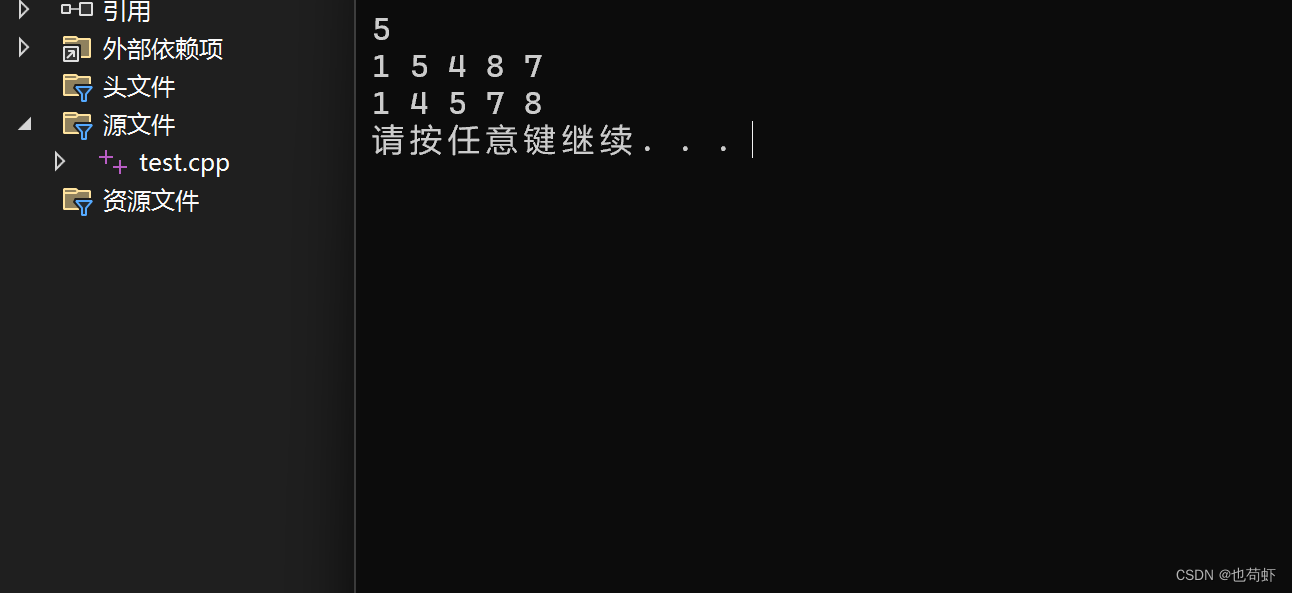
输入及运行结果如下：

好了，今天的分享就到这里，感谢观看，如果喜欢，记得关注哦！