机器学习笔记02--决策树算法(手把手教你看懂)---信息熵，信息增益，增益率，基尼系数_决策树增益系数

目录

1、什么是决策树

2、如何计算信息熵和信息增益

 2.1信息熵：

 2.2信息增益：

 2.3增益率：

 2.4基尼系数

---

        引言：抛开概念，由这个算法的名字我们可以推测一下字面意思，决策树，决策就是有决策能力，树可以理解为我们所学的数据结构中的树，由一个根节点不断往下拓展分支，直到叶子节点为止，叶子节点对应决策结果。那么决策树就是从根节点出发按照当前给定的条件，判断往哪一个分支走，直到遇到叶子节点，说明我们这轮决策结束了。

1、什么是决策树

       引入概念，正如我们引言中所说的那样，当我们引入样本，以及样本的属性（特征），样本的类别，再结合到树中，就可以完美的定义决策树了。假如我们现在有一个数据集，其数据集中有三个样本A，B，C；每个样本对应四个特征F(1), F(2),F(3),F(4)，其样本A对应的特征为F(A1), F(A2),F(A3),F(A4)，样本B对应的特征为F(B1), F(B2),F(B3),F(B4)，样本C对应的特征为F(C1), F(C2),F(C3),F(C4)；数据集对应了两个类别，也就是这三个样本属于两个类别。假设我们根据特征F(1)为根节点来构造决策树，则我们可以以F(1)特征的不同取值为根据，将三个样本进行划分。划分之后，每一个子集在该特征上的取值是一样的，但是他们所属的类别不一定一样，那我们就可以以其他的特征为结点进行划分，直到划分之后的子集所属的类别是一样的，或者是样本的所有特征都用完了但划分之后的子集的类别仍然不相同，那么我们就将该子集中出现的最多的类别作为该叶子节点的类别。

       我们可以以机器学习西瓜书上的西瓜数据集如下图所示，为例说明，有助于更好的理解我上面的叙述。

       首先我们要知道一个决策树是有一个根节点，若干个叶子节点，若干个非叶子节点，也就是不是开始也不是结束的中间节点。

       我们先来分析一下图中西瓜数据集的结构。该数据集有17个样本，每一个样本占一行；首先第一行{色泽，根蒂，敲声，纹理，脐部，触感}是我们每一个样本对应的6个不同的特征(属性)；每一个特征(属性)又有若干个不同的取值。比如色泽这个特征(属性)有{青绿，乌黑，浅白}三个不同的特征取值。

       假设我们构造决策树以色泽这个特征为根节点，那么我们可以把这个数据集D的17个样本划分为三个子数据集，其中第一个子数据集为特征取值为青绿D1={1，4，6，10，13，17}；第二个子数据集为特征取值为乌黑D2={2，3，7，8，9，15}，第三个子数据集为特征取值为浅白D3={5，11，12，14，16}，如下图所示。

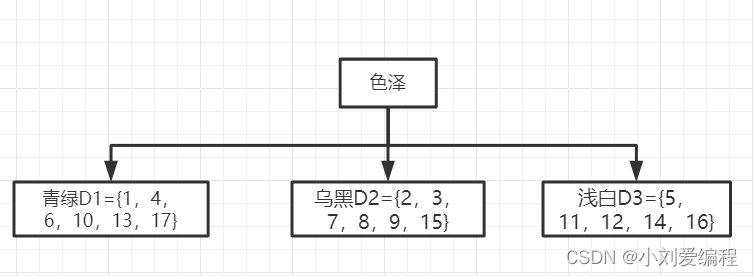
        划分之后，其D1，D2，D3又是独立的三个子数据集，我们对D1数据集进行分析。当前数据集D1如下图所示。其所属的类别有三个是好瓜，有三个不是好瓜，即当前数据集D1中所有样本所属的类别不一样，所以我们可对数据集D1再次进行划分。

        假设我们对数据集D1按照特征(属性)纹理进行划分，则可将数据集D1划分为两个子数据集，分别是特征取值为清晰的子数据集D11={1，4，6，10}，和特征取值为稍糊的子数据集D12={13， 17}。如下图所示。

        划分之后分析数据集D11和D12，如下图所示。我们可以得到数据集D12所属的类别都为不是好瓜；数据集D11，有三个是好瓜，一个不是好瓜。

数据集D11

 数据集D12

       所以对于数据集D12我们可以不需要再进一步的划分数据集，因为他们所属的类别是一样的。可将当前节点标记为叶子节点，其对应的样本类别为：不是好瓜。如下图所示。

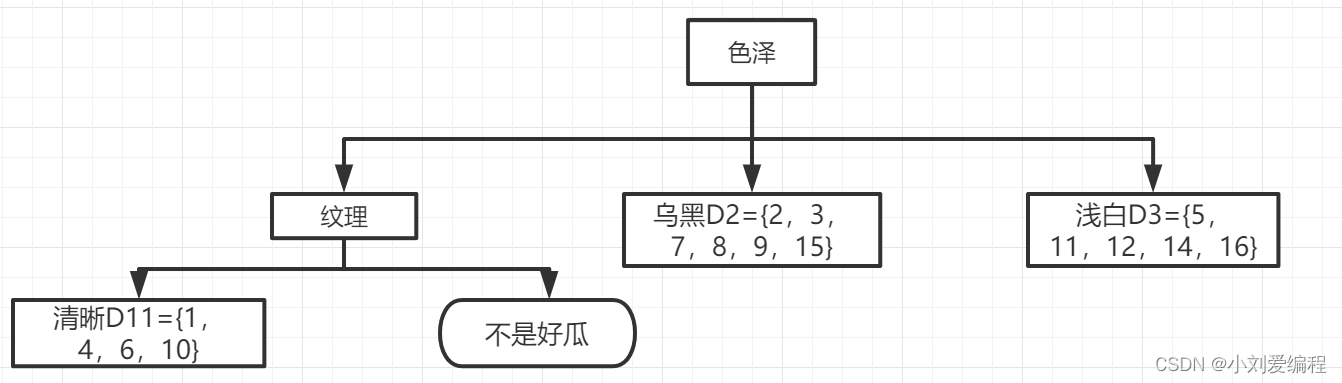
       我们再继续进行分析，其数据集D11按照特征(属性)根蒂进行划分。由于根蒂这个特征的不同取值有三个，所以可将数据集D11划分为三个子数据集Da，Db，Dc；其中特征取值为蜷缩的子数据集Da={1，4}；特征取值为稍蜷的子数据集Db={6}；特征取值为硬挺的子数据集Dc={10}；如下图所示。

         对当前的数据集Da，Db，Dc进行分析，如下图所示。其数据集Da，Db的类别都是一致的都为好瓜，数据集Dc的类别也是全部都一致为不是好瓜。所以我们可以将其数据集Da，Db，Dc所在的节点都标记为叶子节点，即对应一个类别结果。

 Da数据集

 Db数据集

 Dc数据集

注：上面的红色标记的序号是我们在选择特征时候的顺序，标记出来能够更好的看到我们选择特征的顺序。

       由于本次按照特征(属性)根蒂划分之后的数据集Da，Db，Dc其所属的类别都是相同的，所以不需要对这些数据集进行划分，其决策树如下图所示。这里我们只对从原始根结点出发的一个分支D1进行了决策树的构建，其D2，D3和D1分支的构建过程是一样的，可以将其决策树的构建过程看作是递归的。

---

        可能有人在看上面的构建过程会提出疑问。即为什么根节点的特征用色泽，第二个特征用纹理，第三个特征用根蒂？我在使用这些特征时我使用了假设，那肯定会有同学问假设终归是假设，没有说服力。那么我们如何选取某一特征作为我们当前数据集的划分条件呢？

这就引出了我们下面的几个概念----信息熵（熵），信息增益。

2、如何计算信息熵和信息增益

        2.1信息熵：

        用来衡量数据集合纯度的一种方法。纯度就是数据集合中所含样本的类别趋向于一致的程度。在进行决策树构建的过程中，我们当然是希望划分之后的数据集合纯度越高越好。

      假定当前样本集合D中有y个类别，其中第k类的样本在整个集合中所占的比例为pk，那么集合D的信息熵公式如下：

                                                

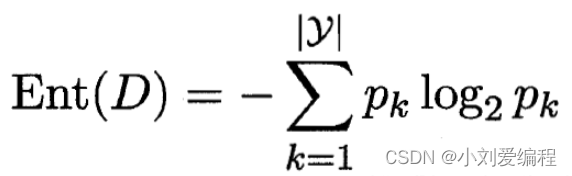
        其公式的意思就是对当前集合D，把每一类的样本数量所占集合D的总数量的比值pk乘以pk的对数，然后对每个类别进行相加，最后取复数。我们可以思考一下，如果当前第k类样本在集合D中所占的比例pk很大，以使得pk接近于1，则该类利用上面公式计算接近于0，该公式计算出来的最小值为0。所以，信息熵Ent(D)的值越小，其纯度越高。

        2.2信息增益：

        由第一部分对西瓜数据集D的分析，我们可以看到一个特征(属性)有若干个不同的取值。比如色泽这个特征(属性)有{青绿，乌黑，浅白}三个不同的特征取值。

        假设当前数据集有若干个不同的特征(属性)，其中一个特征(属性)a有V个不同的取值{a1,a2,...,aV}；如果我们用特征(属性)a对数据集D进行划分，那么我们会产生V个分支，就像是我们第一部分以色泽为特征(属性)进行划分得到了三个分支；其中，第v(小写)个分支节点包含了在数据集D上取特征值为av的样本Dv；在当前分支节点中我们可以以当前数据集Dv计算其信息熵Ent(dv)，用上面的公式；又因为每个分支节点所含的样本的数量不一定相同，所以我们可以计算一个权重分配给各个节点，其权重等于按照当前特征(属性)a取值为av的数据集Dv所含的样本数量与划分前的数据集D所含的样本数量的比值，这样的话可以保证分支节点占有的样本数量越多，则权重就越大。此时，我们就可以计算基于特征(属性)a划分所获得的信息增益。其信息增益计算公式如下。

                             

 信息增益越大，则意味着使用特征(属性)a划分之后的数据集的纯度越大。依据本结论，对于当前节点应该使用哪个特征(属性)划分数据集，我们就可以把每个特征(属性)的信息增益给算一遍，然后挑选出信息增益最大的那个作为该节点数据集划分的特征(属性)。

以上就是著名的ID3决策树学习算法。

如果想要以例子为主，大家可以参考机器学习西瓜书第75页的例子，由于涉及到的运算符号比较麻烦，这里就不过多赘述了，大家可以根据上面的理论进一步的理解体会。

 2.3增益率：

        为什么有了信息增益之后，还有一个增益率呢。假如我们把西瓜数据集的编号也当作样本的特征(属性)，那么按照编号进行划分，可得出其信息增益为0.998，很明显高于其它候选划分属性。因为如果我们按照编号进行划分的话，其编号有几个，那么分支就有几个，而且每个分支都只包含一个样本。但是这样构建出来的决策树并不具有泛化能力，没法对新的样本进行预测。

        信息增益对取值多的特征(属性)具有偏好，为了减少这种偏好带来的不利影响，我们就引入了增益率，其增益率又可称之为著名的C4.5决策树算法。

计算公式如下：

                                                  

其中，属性a的可能取值数目越多，则IV(a)越大。

需要注意的是，增益率准则对可取数目较少的属性有所偏好，因此C4.5算法并不直接选择增益率最大的特征进行划分。而是采用了启发式：先从候选划分特征中找出信息增益高于平均水平的属性。再从中选出增益率最高的。

2.4基尼系数

        引入了基尼系数也就有了新的算法CART决策树。

        在这里数据集D的纯度不再用信息熵来衡量，而是用基尼值来度量，其公式为：

                                             

        由这个公式我们可以看出：Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率。其值越小，则纯度越高。

        而属性a的基尼指数可以定义为如下公式：

                                      

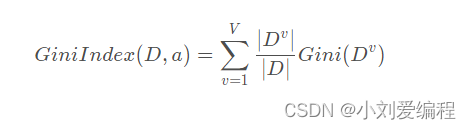
        所以，我们可以对每个特征(属性)计算其基尼指数，把值最小的那个对应的特征(属性)作为我们当前划分的依据。

        这些是关于我们构造决策树时选择属性的一些理论依据，在实际中还会遇到决策树过拟合的问题，那就涉及到了决策树的剪枝处理。即我们要把哪些分支去掉，哪些分支保留。

这是花费了一天的时间写的总结，若转载请注明出处，觉得有用可以分享给需要的人哈，一起学习。