- 1CVSS4.0将于2023年底正式发布_cvss4.0 3.1
- 2数据结构(4.1)——树的性质
- 3OpenssH 漏洞修复_openssh漏洞
- 4深度学习论文导航 | 11 LaneNet:基于实例分割方法的车道线检测网络_基于实例分割的车道线检测算法
- 5c++编码规范(五)_禁止使用rand生成伪随机数
- 6GitHub十大Python项目推荐,Star最高26_github 排行 python
- 7vs code配置MySQL,实现连接、查询等功能
- 8Element UI 消息提示 Message_element-ui message
- 9每天一个数据分析题(四百二十九)- 假设检验
- 10小程序消息推送(含源码)java实现小程序推送,springboot实现微信消息推送_微信小程序发送消息通知 java代码
【目标检测】32、让你一文看懂且看全 NMS 及其变体_nms变体
赞
踩
本博客还有多个超详细综述,感兴趣的朋友可以移步:
目标检测:目标检测超详细介绍
语义分割:语义分割超详细介绍
数据增强:一文看懂计算机视觉中的数据增强
损失函数:分类检测分割中的损失函数和评价指标
Transformer:A Survey of Visual Transformers
机器学习实战系列:决策树
YOLO 系列:v1、v2、v3、v4、scaled-v4、v5、v6、v7、yolof、yolox、yolos、yolop
一、NMS
1.1 背景
NMS 及其变体在边缘检测、关键点检测和目标检测等视觉任务上都有广泛的使用。主要用于剔除和极大值重叠率过大的检测结果。
使用场景:
- 测试
- 推理
分类:
- 类内 NMS
- 类间 NMS
1.2 方法
- 对单张图中的所有检出框按照得分排序(此处说的是类间 NMS,类内的则在每个类内进行操作)
- 以最高得分的框为基准,计算所有框和其 IoU 得分
- 如果某个框和最高得分框的 IoU > 阈值,则将该框类别得分置为 0,即直接剔除该框
- 在剩下的框中再选择得分最高的框,重复进行这种剔除,直到全部结束

1.3 代码
import numpy as np
def nms(dets, Nt):
x1 = dets[:,0]
y1 = dets[:,1]
x2 = dets[:,2]
y2 = dets[:,3]
scores = dets[:,4]
order = scores.argsort()[::-1]
#计算面积
areas = (x2 - x1 + 1)*(y2 - y1 + 1)
#保留最后需要保留的边框的索引
keep = []
while order.size > 0:
# order[0]是目前置信度最大的,肯定保留
i = order[0]
keep.append(i)
#计算窗口i与其他窗口的交叠的面积
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
#计算相交框的面积,不相交时用0代替
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
#计算IOU:相交的面积/相并的面积
ovr = inter / (areas[i] + areas[order[1:]] - inter)
inds = np.where(ovr < thresh)[0]
order = order[inds + 1]
return keep
# test
if __name__ == "__main__":
dets = np.array([[30, 20, 230, 200, 1],
[50, 50, 260, 220, 0.9],
[210, 30, 420, 5, 0.8],
[430, 280, 460, 360, 0.7]])
thresh = 0.35
keep_dets = nms(dets, thresh)
print(keep_dets)
print(dets[keep_dets])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
1.4 不足
1、稠密场景会出现漏检:因为稠密场景的目标本身重合就比较大,会把置信度较小但为真实目标的框筛掉
2、实际效果容易被阈值影响:NMS 的阈值是人为设定的,阈值过大会出现误删,阈值过小会出现误检,对 mAP 有很大影响。
3、分类得分和 IoU 的割裂使用,盲目认为得分最大的框的定位也是最准确的,忽略了得分低的框的定位也可能是准确的
二、Soft NMS
论文:Soft-NMS:Improving Object Detection With One Line of Code
出处:ICCV2017
2.1 背景
由于 NMS 的剔除方法过于暴力,可能剔除掉真正定位准确的框,导致保留的框不准确或漏检的问题,如图 1 所示。故此,作者提出了 soft-NMS,不直接删除 IoU 大于阈值的框,而是降低其分类得分,用以缓解漏检的情况。

2.2 方法
NMS 的处理方法:
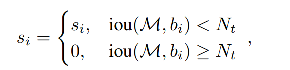
Soft NMS 的处理方法:
首先选择得分最大的框 M,并计算所有框和 M 的 IoU,对于 IoU>阈值的框,将其分类得分适当降低,而非直接剔除,来避免漏检的情况。
具体是如何降低得分的呢(只降低 IoU > 阈值的框的得分):
- 对于 IoU 越大的框,得分降低的越多
- 对于 IoU 越小的框,得分降低的越少
为什么这样降低:
- 当一个框和 M 的 IoU 越大的时候(如0.9),那么它们越有可能属于同一目标,越应该被剔除,而 soft NMS 是狠狠的降低其分类得分
- 当一个框和 M 的 IoU 不是很大的时候(如0.7),那么它们越有可能不属于同一目标,可能是相邻很近的互相遮挡的不同目标,越不应该将其剔除,所以 soft NMS 稍微降低了其分类得分
从下面的公式来分析:
- 当 IoU 越大,(1-IoU) 越小,则和 s i s_i si 相乘后越小,修正后的分类得分越小
- 反之亦然
第一种加权方式:线性加权
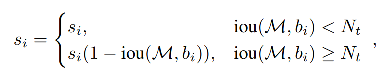
但上面的公式在阈值 N t N_t Nt 处是不连续的,所以作者使用高斯惩罚函数,为什么是不连续的:
- 其实 IoU 可以看做是一个惩罚项,当 IoU 阈值很小,且 IoU 很小甚至没有重叠的时候,惩罚项很小。但当 IoU 很大的时候,惩罚项也就会很大。
- 所以,需要一个可以缓冲的函数,让 M 对其他框的得分的影响是逐步变化的,对 IoU 很小的框影响很小。
所以作者使用高斯的方式来对得分进行修正:
第二种加权方式:高斯加权:
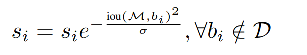
- iou 越大,加权值越小,修正后的得分降低的越多
- iou 越小,加权值越大,修正后的得分降低的越少
作者经过实验证明,高斯加权的方式更优,所以使用了高斯加权的方式。
Soft NMS 的过程如下:
其中, f ( i o u ( M , b i ) ) f(iou(M, b_i)) f(iou(M,bi)) 是基于重叠率的加权函数。

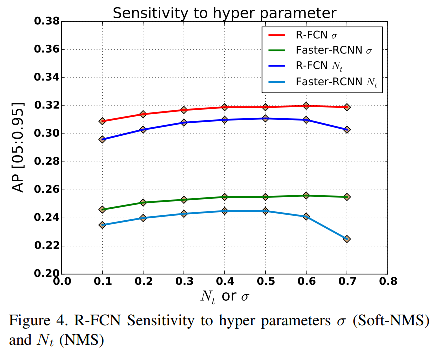
2.3 效果
Soft-NMS 的超参数设置:
- 在使用线性加权时,设定 IoU 阈值 N t = 0.3 N_t=0.3 Nt=0.3
- 在使用高斯加权时,设定高斯函数的 δ = 0.5 \delta=0.5 δ=0.5, δ \delta δ 越大,开口越大, δ \delta δ 越小,开口越小
2.4 代码
# -*- coding:utf-8 -*-
import numpy as np
def py_cpu_softnms(dets, Nt=0.3, sigma=0.5, thresh=0.5, method=2):
"""
py_cpu_softnms
:param dets: boexs 坐标矩阵 format [x1, y1, x2, y2, score]
:param Nt: iou 交叠阈值
:param sigma: 使用 gaussian 函数的方差
:param thresh: 最后的分数阈值
:param method: 使用的方法,1:线性惩罚;2:高斯惩罚;3:原始 NMS
:return: 留下的 boxes 的 index
"""
N = dets.shape[0]
# the order of boxes coordinate is [x1,y1,x2,y2]
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
for i in range(N):
# intermediate parameters for later parameters exchange
tB = dets[i, :4]
ts = dets[i, 4]
ta = areas[i]
pos = i + 1
if i != N-1:
maxscore = np.max(dets[:, 4][pos:])
maxpos = np.argmax(dets[:, 4][pos:])
else:
maxscore = dets[:, 4][-1]
maxpos = -1
if ts < maxscore:
dets[i, :] = dets[maxpos + i + 1, :]
dets[maxpos + i + 1, :4] = tB
dets[:, 4][i] = dets[:, 4][maxpos + i + 1]
dets[:, 4][maxpos + i + 1] = ts
areas[i] = areas[maxpos + i + 1]
areas[maxpos + i + 1] = ta
# IoU calculate
xx1 = np.maximum(dets[i, 0], dets[pos:, 0])
yy1 = np.maximum(dets[i, 1], dets[pos:, 1])
xx2 = np.minimum(dets[i, 2], dets[pos:, 2])
yy2 = np.minimum(dets[i, 3], dets[pos:, 3])
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
ovr = inter / (areas[i] + areas[pos:] - inter)
# Three methods: 1.linear 2.gaussian 3.original NMS
if method == 1: # linear
weight = np.ones(ovr.shape)
weight[ovr > Nt] = weight[ovr > Nt] - ovr[ovr > Nt]
elif method == 2: # gaussian
weight = np.exp(-(ovr * ovr) / sigma)
else: # original NMS
weight = np.ones(ovr.shape)
weight[ovr > Nt] = 0
dets[:, 4][pos:] = weight * dets[:, 4][pos:]
# select the boxes and keep the corresponding indexes
inds = np.argwhere(dets[:, 4] > thresh)
keep = inds.astype(int).T[0]
return keep
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
2.5 不足
优势:
- 相比 NMS,提升了 recall
- 缓解了重叠目标的漏检情况
不足:
- 仍然需要手工选取的阈值/高斯方差
三、Softer NMS
论文:Bounding Box Regression with Uncertainty for Accurate Object Detection
代码:https://github.com/yihui-he/KL-Loss
出处:CVPR2019
3.1 背景
由于 NMS 的三个问题:
- 密集场景漏检多
- 使用分类得分来判定一个框的定位效果,原理上是未对齐的
- 标注框并非总是准确的
soft NMS 通过降低距离近的框的得分,而非直接剔除该框的方法,缓解了第一个问题,所以 Softer NMS 被提出,以 “标注框并非准确,会有一定不确定性” 为前提,来通过定位的方差投票来进行位置修正。
3.2 方法
Softer NMS = soft NMS + variance voting
1、针对边分布不确定性问题:使用高斯分布来表示框的每个边的位置,使用 KL-Loss 来学习位置的分布(这个分布就包括位置可不确定性——即方差)
为了通过位置来估计出位置得分,本文的网络会预测一个概率分布,而非 bbox 的位置。
预测的概率分布简化为一个高斯分布:
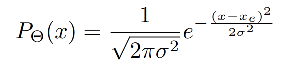
其中:
- Θ \Theta Θ 是可学习的参数
- x e x_e xe 是估计的 bbox 位置
- σ \sigma σ 为标准差,也表示了不确定性, σ → 0 \sigma \to 0 σ→0,说明网络预测的位置越准确,置信度越高。
真实的位置也可以被建模为一个特殊的高斯分布, σ → 0 \sigma \to 0 σ→0, 就是 Dirac delta 分布:
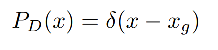
其中: x g x_g xg 是 bbox 的真实位置
Dirac delta 分布: 在 0 处无限大,在其他位置为 0
特性: ∫ δ ( x ) d x = 1 \int \delta(x)dx=1 ∫δ(x)dx=1
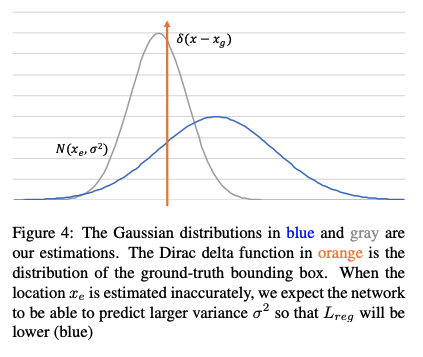
- 橘色为真值
- 灰色预测较准,方差较小,位置距离真值的位置较近
- 蓝色预测较差,方差较大,位置距离真值的位置较远
KL Loss 如何计算:
上面将预测结果和真实label建模后,就可以使用 N 个采样点来估计出参数 Θ ^ \hat{\Theta} Θ^,最小化预测和真实分布的 KL 距离:
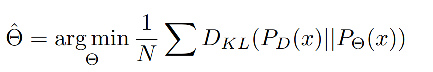
KL 散度是用于框位置的回归的:
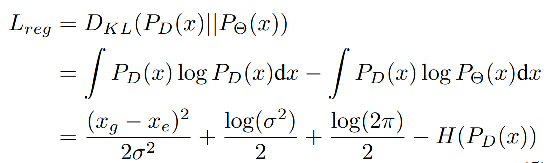
当网络预测一个较大的方差 σ 2 \sigma^2 σ2 时, L r e g L_{reg} Lreg 会很小,位置 x e x_e xe 的估计会更准确。如上图 4 所示。
由于 L r e g L_{reg} Lreg 不依赖于后两项,则有如下规律:
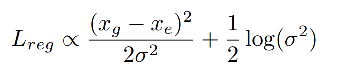
当 σ = 1 \sigma=1 σ=1 时,KL loss 演变成一个规范的 Euclidean loss:
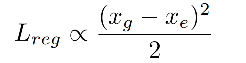
该 loss 函数是和估计的位置和位置标准差相关的:
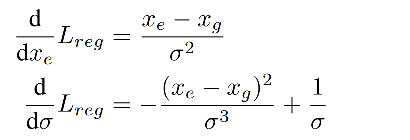
由于 σ \sigma σ 是分母,所以在刚开始训练的时候可能会梯度爆炸,为了避免,作者使用 α = l o g ( σ 2 ) \alpha = log(\sigma^2) α=log(σ2) 而非 α = σ \alpha=\sigma α=σ:
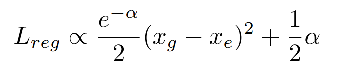
当 ∥ x g − x e ∥ > 1 \|x_g-x_e\|>1 ∥xg−xe∥>1 时,使用的函数类似于 smooth L1 loss:
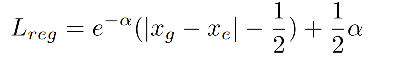
在开始训练的时候,使用随机高斯来初始化 FC 层参数,标准差设置为 0.0001,均值设置为 0,此时 KL loss 和 smooth L1 loss 类似。
KL loss 的三个优势:
- 能够很好的捕捉数据集中的不确定性: bbox 回归器能从不确定的 bbox 中拿到很小的 loss
- 学习到的方差在后处理中很有用:作者提出了方差投票(variance voting),在 NMS 的时候,使用该预测出来的方差来给其邻域的位置加权,来给候选框投票
- 学习到的概率分布是可解释的:因为其反应了预测框的不确定程度,对很多下游任务(自动加速、机器人)很有必要
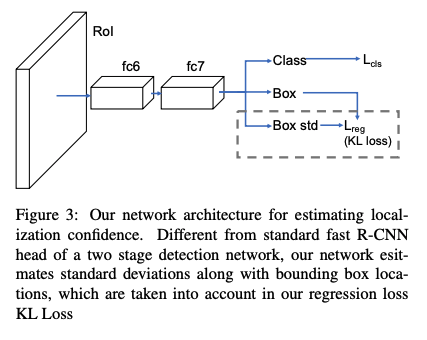
2、针对分类得分和定位得分使用未对齐的问题:使用方差投票
Var voting:得分修正(soft NMS )+ 位置修正(给距离候选框近的框分配更高的权重,其不确定性更小)
第一步:首先进行 soft NMS:
Soft NMS:对大于 IoU 阈值的框得分抑制(线性和高斯两种方式,高斯更优),小于 IoU 阈值的框得分不变
soft NMS 认为和候选框距离越近的框,越有可能是”假正”,对应分数的衰减应该更严重,所以对得分进行衰减。
-
衰减方式 1:使用1-IoU与得分的乘积作为衰减后的值:参数为 N t = 0.3 N_t=0.3 Nt=0.3
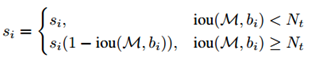
当相邻检测框与候选框重叠超过阈值 N t N_t Nt 时,得分线性衰减,但该函数并非线性函数,容易产生突变,所以需要找到一个连续的函数,对没有重叠的框的得分不衰减,对高度重叠的框进行较大的衰减,即高IoU的有高的惩罚,低IoU的有低的惩罚,且是逐渐过渡的,所以就有了第二种。
-
衰减方式 2:高斯惩罚函数:参数为 δ = 0.5 \delta=0.5 δ=0.5
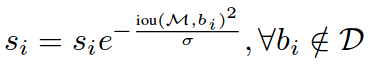
第二步:完成了 soft-NMS 后,对得到的边框 b m b_m bm 进行基于网络学习到的方差进行修正。
预测结果为:
( x 1 , y 1 , x 2 , y 2 , s , σ x 1 , σ y 1 , σ x 2 , σ y 2 ) (x_1, y_1, x_2, y_2, s, \sigma_{x_1}, \sigma_{y_1}, \sigma_{x_2}, \sigma_{y_2}) (x1,y1,x2,y2,s,σx1,σy1,σx2,σy2)
新的坐标计算如下, x i x_i xi 是第 i i i 个框的坐标( σ t \sigma_t σt 是可调节参数):
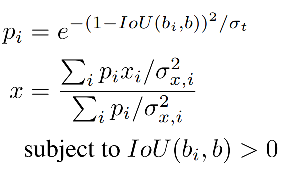
-
首先,选择出分类得分最大的框 b b b
-
然后,对所有和 b b b 存在 IoU 交集的框 ( I o U ( b i , b ) IoU(b_i, b) IoU(bi,b) >0),计算权值 p i p_i pi
- I o U ( b i , b ) IoU(b_i, b) IoU(bi,b) 越大,则 p i p_i pi 越大,即距离越近的两个框产生的 p i p_i pi 值越大,权重越大,也就是说距离越近的框,对 b b b 的最终位置影响更大。
- 方差 σ x , i \sigma_{x,i} σx,i 越大,则权重越小,也就是会对 b b b 的最终位置影响更小。
-
最后,根据权值,来更新 b b b 的坐标(四个坐标分别更新)
作者给距离真值更近但分类得分低的框权重更高。
有两种邻域框会被降权重:
- 有高方差的框
- 和候选框的 IoU 更小的框
分类得分不参与投票,因为低分类得分可能有高位置得分。

四、IoU-Net:IoU-Guided NMS
论文:Acquisition of Localization Confidence for Accurate Object Detection
出处:ECCV2018
4.1 背景
首先,由于一般的 NMS 是用分类分数来主导一个框的去留,想当然的选择得分高的框作为最优的框,忽略了得分高并不一定定位准的现象,如下图 1a 所示。
其次,在整个重复去留的过程中,没有一个定位质量的衡量标准,所以最终回归得到的框可解释性较差,如图 1b 所示,可能经过多次迭代反而得到了更不好的框。

4.2 方法
基于上述背景,研究者提出了 IoU-Net,让网络和关系分类得分一样关心定位得分。
1、原理分析:
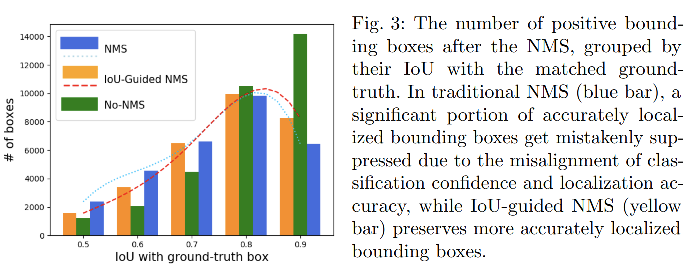
作者首先分析了 IoU-Classification 的关系和 IoU-Localization 的关系:
如图 2a 所示,是在进行 NMS 之前的框的统计结果,Person 相关系数展示出定位的准确性和分类得分是没有强关联的,因为选择两阶段检测器选择正负样本是根据一个 IoU 阈值来确定的,并非定位准确性来确定的,所以这样的效果很容易理解。
如图 2b 所示,作者提出了 IoU-Net 来预测每个框的定位得分(也就是预测 IoU),低 IoU 的框对应的定位得分一般也比较低。
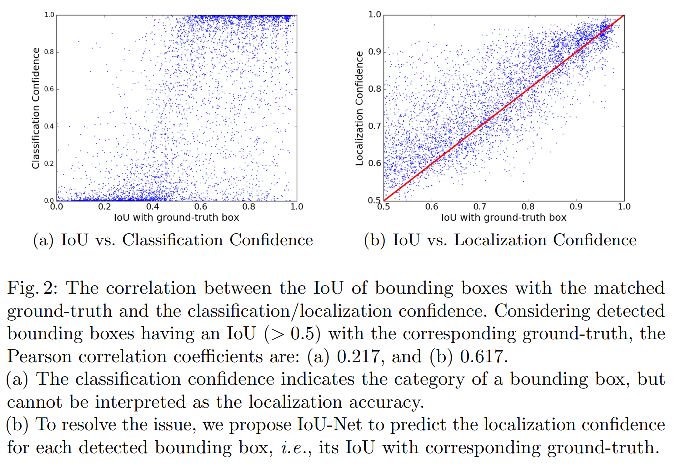
图 3 展示了在 NMS 前后保留的 positive 框的数量,横轴是预测框和 gt 框的 IoU.
这些框是依据 IoU 聚拢的,当多个框对应一个真值框的时候,只将 IoU 最大的那个框认为是 positive 的。
从图中可以看出,有很多 IoU>0.9 的框被 NMS 滤掉了(这些其实是定位优质的框,但却被滤掉了),这会严重损害最终的定位效果。
2、IoU-Net
① 使用 class-aware IoU 预测器来预测 IoU
class-aware IoU 预测器:两层的网络
- 输入: FPN 特征
- 输出:对每个框的定位准确性预测(IoU)
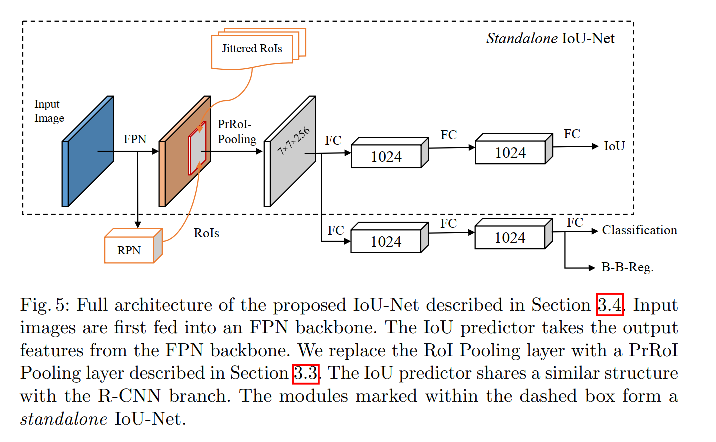

② IoU-Guided NMS
为了解决分类得分和定位准确率没对齐的问题,IoU-Guided NMS,将分类得分和定位得分(IoU 预测结果)进行了解耦,使用预测的定位得分作为框排序的标准。
方法:
- 选择预测的 IoU 最大的框 M 作为基准框
- 将和 M 的 IoU 大于阈值的框,消除,当框 i 把框 j 消除后,将框 i 的分类得分更新为 m a x ( s i , s j ) max(s_i, s_j) max(si,sj),即这两个框中的最大得分,这种操作可以看出得分聚合:当多个框都对应一个真值时,使用最大的得分作为最终得分。
优势: 对分类得分和定位得分解耦,避免了两者不对齐的问题,提升了效果
五、FCOS:Centerness-NMS
论文:FCOS: Fully Convolutional One-Stage Object Detection
代码:https://github.com/aim-uofa/AdelaiDet/tree/master/configs/FCOS-Detection
出处:ICCV2019
5.1 背景
FCOS 是单阶段检测器,在只有分类和回归 loss 时,和两阶段检测器效果还有一定的差距,主要原因在于预测产生了很多距离目标中心点很远的低质量 bbox。
所以作者就提出了 centerness 分支,来预测每个预测框和真实框的 centerness 特征,即预测框和真实目标中心点的位置。
5.2 方法
centerness 如何在 NMS 中使用
使用方法: 在测试时,和分类得分相乘,然后对框进行排序,距离越远的框得分会被很大程度地抑制下去,可以看做 centerness-NMS。
centerness 公式如下:
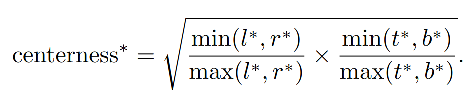
- 为了减缓衰落,使用了根号
- centerness 的范围是 (0,1),使用二值交叉熵损失来训练(添加到公式 2 的 loss 函数)
- 在测试时,final score(用于 NMS 框排序)是 centerness × classification score 得到的,所以可以降低远离中心点的位置(即 low-quality 位置)的权重,可以通过 NMS 过滤掉很大一部分 low-quality 位置,提升检测效果。
极端情况下:
- 如果某一个点在box边界,那么centerness就是0
- 如果刚好在box中心,这个值就是1。centerness的值在0-1之间
- 测试的时候,作者将 centerness 乘以类别 score 作为新的 score,这样就降低了远离中心点的 location 的分数,在NMS阶段将会大概率过滤掉它们。
从 anchor-based 检测器的角度来看,anchor-based 方法使用两个 IoU 阈值来将 anchor 分为 negative、ignore、positive,centerness 可以被看做一个 soft threshold。

使用 centerness 参与 NMS 的效果分析:
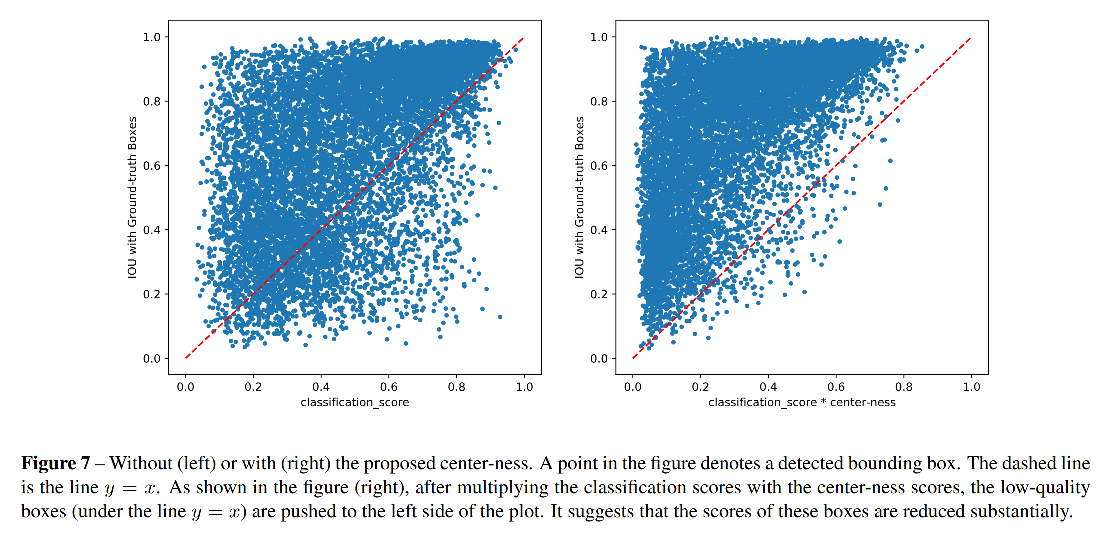
如图 7 所示:
- 使用 centerness 前,有很多 low-quality bbox 的类别得分很高,很难被 NMS 消除
- 使用 centerness 后,这些点都被推到了左上角,即降低类别得分置信度,更容易被消除
六、GFLV1:Classification-IoU-NMS
论文: Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
代码:https://github.com/open-mmlab/mmdetection/tree/master/configs/gfl
出处:NIPS2020
6.1 背景
单阶段目标检测器是将目标检测建模为了一个密集的分类和定位任务,分类使用 Focal loss,定位可以看做学习 Dirac 分布。
很多单阶段检测器由于没有预设的 anchor,导致定位效果较差,所有很多方法都引入了单独的预测分支来衡量定位的效果,如FCOS 中使用 centerness 来评估定位质量,然后在 NMS 排序时,将 centerness 和 分类 得分相乘,用于排序。
所以,主流单阶段检测方法有三个基础的元素:
- 检测框的定位质量(如 IoU-Score 或 centerness score)
- 分类
- 定位
6.2 方法
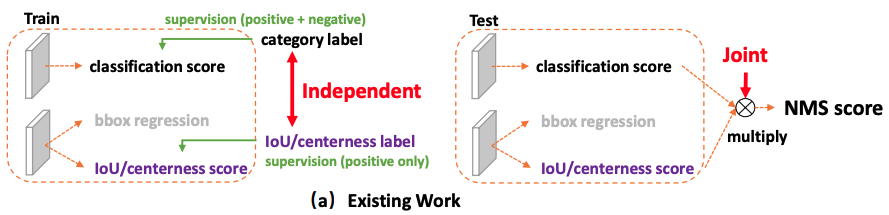
针对主流算法问题 1:训练和测试不一致性
虽然 FCOS 中使用了 centerness × \times × score 的形式,为 NMS 引入了位置的质量信息,但测试和训练过程还是存在一定的不一致性:
1、用法不一致:
- 训练时:分类得分用于训练分类分支,定位得分和centerness得分用于训练回归分支
- 测试时:分类得分和定位得分相乘,来对框进行排序
2、对象不一致:
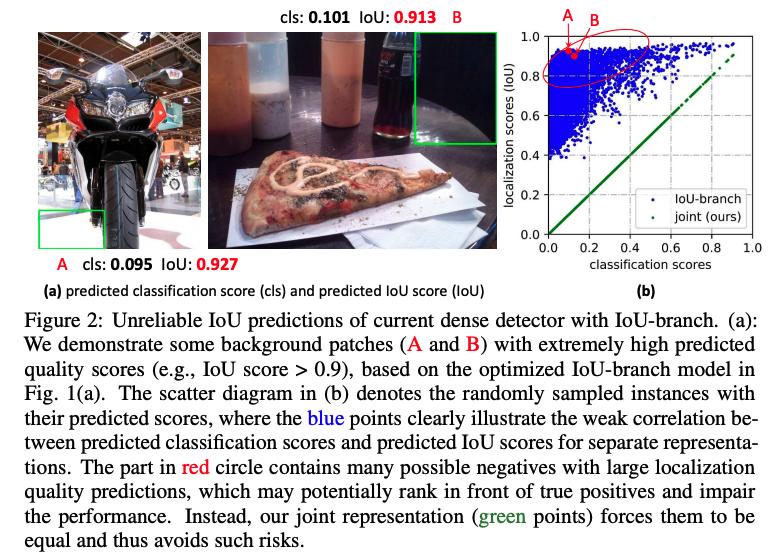
- Focal loss 能够使得分类分支上,少量正样本和大量负样本一起训练,但框的质量估计是只针对正样本的。而在 NMS 排序的时候,是分类得分和定位得分联合使用的,会导致必然存在一部分分数很低的负样本的定位质量在训练过程中没有监督信号,即大量负样本没有定位质量的度量,这就会导致一个分类得分很低的负样本,由于预测了一个高定位得分,被导致预测为一个正样本。
问题 1 解决方法:
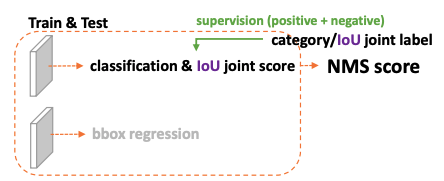
建立一个 classification-IoU joint representation
对于第一个训练和测试不一致的问题,为了保证训练和测试一致,同时还能兼顾分类和框质量预测都能训练到所有的正负样本,作者提出将框的表达和分类得分结合起来使用。
当预测的类别为 ground-truth 类别的时候,使用位置质量的 score 作为置信度,本文的位置质量得分就是使用 IoU 得分来衡量。
针对主流算法问题 2:对框回归建模不够灵活(如 softer-NMS 使用高斯分布建模框的边的位置),没办法建模复杂场景的不确定性
解决方法:直接回归一个任意分布来建模框的表示
方法:使用 softmax 来实现,涉及到从狄拉克分布的积分形式推导到一般分布的积分形式来表示框
这样一来,就消除了训练和测试的不一致性,而且建立了如图 2b 的分类和定位的强相关性。
此外,负样本可以使用 0 quality scores 来监督。
Generalized Focal Loss 的构成:
QFL:Quality Focal Loss,学习分类得分和位置得分的联合表达,可以用于 NMS 中辅助框排序
DFL:Distribution Focal Loss,将框的位置建模成一个 general distribution,让网络快速的聚焦于和目标位置距离近的位置的分布
为什么 IoU-branch 比 centerness-branch 效果更好?
- IoU 本身就更适合衡量定位效果
- Centerness label 过小导致正样本漏检
centerness 是 FCOS 中提出的用于衡量预测框中心点和 gt 框中心点距离的指标,GFLv1 中 的 预测IoU 是对预测框定位质量的预测,上面的实验的证明了 IoU 效果更好一些,这是为什么呢?
本文作者通过分析后发现,主要原因在于对于极小的物体,centerness 的 label 非常小,难以被优化,如图 11 所示。
为什么 label 小的时候难以被优化,或者说会降低网络的查全率呢,因为如果一些正样本的 centerness label 本来就很小,那么在 NMS 的时候,乘到 classification score 上,会拉低排序的得分,导致这些正样本被排到后面,就会漏检。
七、GFLV2:DGQP-NMS
代码:https://github.com/implus/GFocalV2
出处:CVPR2021
7.1 背景
GFLV1 中提出的 generalized 分布,用于将位置分布建模为一个更通用的分布,且发现了边界模糊与否和位置分布的关系(越模糊,分布越平缓),但没有好好用这个分布。GFLV2 使用了这个分布的统计信息,来提取位置得分,指导模型训练。
7.2 方法
GFLV 1 的 NMS 排序方式:
GFLV1 是使用了 classification-IoU 的联合表达方式,来缓解训练和测试的不一致性,方式如下,当预测类别是真实类别时,联合表示特征 J = I o U J=IoU J=IoU,否则为 0。
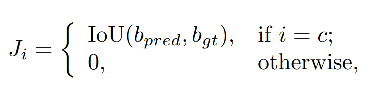
V1 这种方式虽然进行了联合使用,但还是有局限性的
GFLV2 的 NMS 排序方式:
V2 同时使用分类得分(C)和由 Distribution-Guided Quality Predictor (DGQP) 得到的位置质量得分(I)作为联合表达,且同时用于训练和测试,不会有不一致性。
J = C × I J=C \times I J=C×I
- C C C 是分类得分
- I I I 是由 DGQP 得到的定位质量估计,如下图红框里边所示即为 DGQP
- 在进行 NMS 排序时,同时考虑分类得分和定位质量,分类得分大但定位质量低的框会被拍到后面,分类得分略低但定位质量高的框会被提到前面来,避免了使用分类来判断位置的问题。
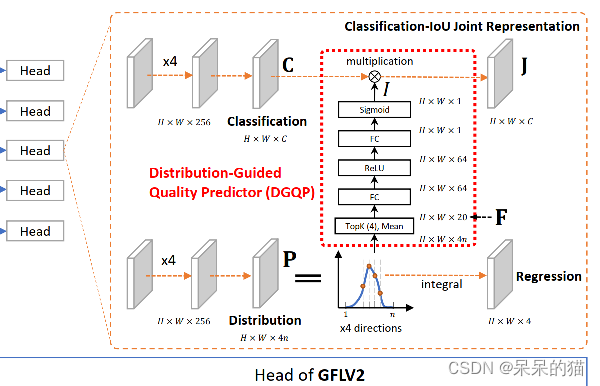
DGQP 的原理:
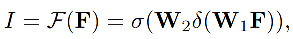
- 输入:位置的统计信息
- 输出:定位质量估计
- 原理:将输入分布的 Top-k 值和均值 concat 起来,作为分布的特征,然后经过两个全连接层+Relu+Sigmoid,得到输出。
为什么使用 Top-k 值和均值:
能很好的反应分布的形态(如大小缓陡等),且对偏移不敏感,对尺度有更好的鲁棒性。
DGQP-NMS 的优势:
- 相比 V1 来说,能够降低学习难度,加速模型训练
- 发现了输入和输出之间的强联系,能够很好的使用输入分布,来指导得到定位质量,且定位质量相比使用单一的 IoU 或 centerness 等更可靠



