【概率论与统计学】最常用常考的6种概率计算 经验分享_统计学中计算概率

本文介绍在概率论与数理统计，统计学这两门课中，以及平时的作业中最常用的两种需要加以应用的六种概率。按照数据的类型可以分为两类，一类是针对连续型变量（均匀分布、指数分布、正态分布），另一类则针对离散型变量（0-1分布、二项分布、泊松分布）。

一、离散型变量

1、二项分布

在每次试验中只有两种可能的结果，而且两种结果发生与否互相独立互斥，每次的实验结果都互不影响无关，事件发生与否的概率在每一次独立试验中都保持不变。
期望E（X） = np 方差D（X） = np（1-p）；

2、0-1分布

已知随机变量X，其中P{X=1} = p，P{X=0} = 1-p，其中 0 < p < 1，则成X服从参数为p的0-1分布。是一种特殊的二项分布，当试验次数为1时，二项分布服从0-1分布。
期望为E（X） = p 方差D（X） = p（1-p）；

3、泊松分布

设随机变量Xn~B(n,pn)(n=1,2,3…),（其中pn为与n相关的概率，并满足当n趋向于无穷大时n*pn的极限等于k的条件），则有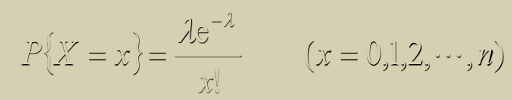
其中方差和期望均为k。

二项分布只有在n很大，p很小时，才能用泊松分布来进行近似，而越趋于这种情况近似程度越明显。也即可以通过“二项分布在n和p满足一定条件时可以进化为泊松分布”来联系起来。

要区别的是：二项分布和泊松分布是离散型分布,正态分布是连续分布，不能说二项分布和泊松分布是一种正态分布。

二、离散型变量

4、均匀分布

若连续型随机变量X具有概率密度

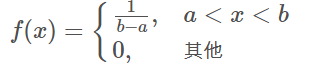
则称X在（a，b）上服从均匀分布

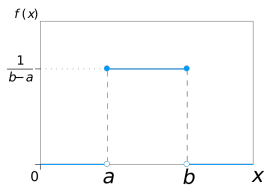
f(x)的“均匀”可以理解为，一个变量落在[a,b]内任何等长度的区间内概率都是相等的。此外，因为概率密度函数与x轴围成的区域面积一定是1，长度是b-a，那么高度即f(x)的值就是1/(b-a)了。

其中期望E（X） = （a+b）/ 2 ，方差D（X） = （b-a）^2 / 12。

5、指数分布
若某随机变量X具有概率密度如下

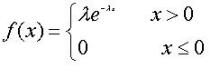
其中λ>0，就称X~exp(λ)。期望值E(x)=1/λ， D(x)=1/λ^2。推导如下：

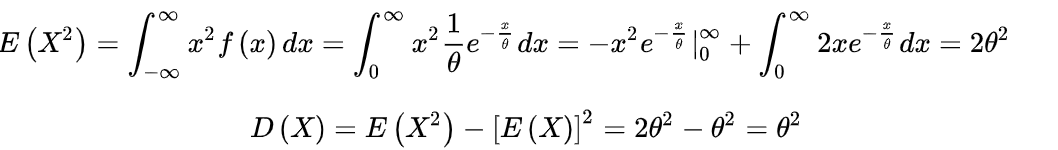指数分布最重要的特征就是服从这一分布的随机变量会具有无记忆性，即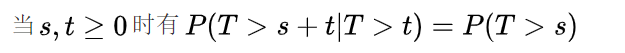
无记忆性推导如下：

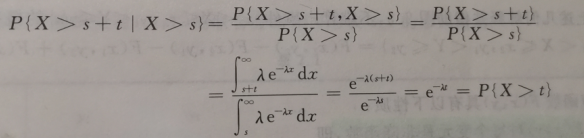
可以理解为X>s的条件不影响X>s+t的概率；进一步举例：若已知某个人活了S岁，那么这个人还能再活t年的概率与其任何时候还能活t年的概率是一样的；假设你和某人约会，你已经等了某个人30分钟，那么它再让你等t分钟与刚开始时让你等t分钟的概率是相同的。可以与“沉没成本”的概念进行联系。

6、正态分布
若随机变量概率密度函数为: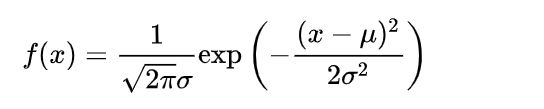

则（此为以为正态分布下的情况）

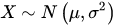
标准正态分布曲线中，面积与方差有如下关系
横轴区间（μ-σ,μ+σ）内的面积为 68.268949%。
P{|X-μ|<σ}=2Φ（1）-1=0.6826
横轴区间（μ-2.58σ,μ+2.58σ）内的面积为 95.449974%。
P{|X-μ|<2σ}=2Φ（2）-1=0.9544
横轴区间（μ-3σ,μ+3σ）内的面积为 99.730020%。
P{|X-μ|<3σ}=2Φ（3）-1=0.9974

常用的F(x<=1)=0.8413

以上公式的推导过程可以参考：
概率论各种基础分布期望和方差推导过程汇总