商汤科技python实习生面试经验_商汤科技python面试

电话面试。
自我介绍不说了（985丢人高校成绩前50%）
在校项目经历和主要在做什么，比较关注你在项目中主要用了哪些东西，什么技术？
（我只在一家小公司实习做了一个torando项目，在校有做一个比较水的机器学习项目和一个推荐算法）
会的技术（java,c,python中间表示会做爬虫和web、数据库用过mysql和mongodb）
自我评价（这个随便答得哈哈）
1.浏览器输入网址访问时，发生了什么？
答：先通过dns服务器访问到ip地址（他这里追问dns可以只访问本地吗，其实有个坑，就是通过本地缓存代理的方式，当时没想到，就直接答了要访问供应商的dns数据库查ip）
然后浏览器发送报文，建立TCP连接，3次握手
然后胡说了一堆wsgi网关的一些东西，服务器端回调函数什么的啊
之后交给浏览器渲染
2.一个算法题，不递减数组的二分查找，找到一个给定数字（有重复）index，找出首位index和末尾index，时间复杂度Logn，找不到返回-1,-1
之前只了解一般的二分查找算法，没有太多研究，陷入纠结。
这个时间复杂度比较低，一开始想到的是分治递归，将查找结果递归到前一半，后一般，或者首部在前，末尾在后，但是编码比较困难。
面试小哥提示了一下。可以考虑先找首位，如果为logn，则找末尾也是logn。
根据提示，大概写了下算法，就是先找到一位符合的数字，再线性倒推后者前推过去，代码有点bug，但是小哥似乎不太在意，认为大致满足要求。
然后面试官本来准备再问一道题的，看时间12点，就溜了吃饭了。

我的解法是有bug，如果线性前推和倒推，在某些极端条件下，是不满足logn时间复杂度的。
正确解法：（转自知乎）
作者：labuladong
链接：https://www.zhihu.com/question/36132386/answer/712269942
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

零、二分查找框架

'''c
int binarySearch(int[] nums, int target) {
int left = 0, right = ...;
while(...) {
    int mid = (right + left) / 2;
    if (nums[mid] == target) {
        ...
    } else if (nums[mid] < target) {
        left = ...
    } else if (nums[mid] > target) {
        right = ...
    }
}
return ...;
1
2
3
4
5
6
7
8
9
10
11
12
13
14

}分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。本文都会使用 else if，旨在讲清楚，读者理解后可自行简化。其中 … 标记的部分，就是可能出现细节问题的地方，当你见到一个二分查找的代码时，首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。另外声明一下，计算 mid 时需要技巧防止溢出，可以「参见前文」，本文暂时忽略这个问题。
一、寻找一个数（基本的二分搜索）这个场景是最简单的，肯能也是大家最熟悉的，即搜索一个数，如果存在，返回其索引，否则返回 -1。

   '''c
int binarySearch(int[] nums, int target) {
int left = 0; 
int right = nums.length - 1; // 注意
   while(left <= right) { // 注意
    int mid = (right + left) / 2;
    if(nums[mid] == target)
        return mid; 
    else if (nums[mid] < target)
        left = mid + 1; // 注意
    else if (nums[mid] > target)
        right = mid - 1; // 注意
    }
return -1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14

}为什么 while 循环的条件中是 <=，而不是 < ？
答：因为初始化 right 的赋值是 nums.length - 1，即最后一个元素的索引，而不是 nums.length。这二者可能出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间 [left, right]，后者相当于左闭右开区间 [left, right)，因为索引大小为 nums.length 是越界的。我们这个算法中使用的是前者 [left, right] 两端都闭的区间。这个区间其实就是每次进行搜索的区间。什么时候应该停止搜索呢？当然，找到了目标值的时候可以终止：if(nums[mid] == target)
return mid;但如果没找到，就需要 while 循环终止，然后返回 -1。那 while 循环什么时候应该终止？搜索区间为空的时候应该终止，意味着你没得找了，就等于没找到嘛。while(left <= right) 的终止条件是 left == right + 1，写成区间的形式就是 [right + 1, right]，或者带个具体的数字进去 [3, 2]，可见这时候区间为空，因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的，直接返回 -1 即可。while(left < right) 的终止条件是 left == right，写成区间的形式就是 [left, right]，或者带个具体的数字进去 [2, 2]，这时候区间非空，还有一个数 2，但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。当然，如果你非要用 while(left < right) 也可以，我们已经知道了出错的原因，就打个补丁好了：//…
while(left < right) {
// …
}
return nums[left] == target ? left : -1;为什么 left = mid + 1，right = mid - 1？我看有的代码是 right = mid 或者 left = mid，没有这些加加减减，到底怎么回事，怎么判断？
答：这也是二分查找的一个难点，不过只要你能理解前面的内容，就能够很容易判断。刚才明确了「搜索区间」这个概念，而且本算法的搜索区间是两端都闭的，即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时，如何确定下一步的搜索区间呢？
当然是 [left, mid - 1] 或者 [mid + 1, right] 对不对？因为 mid 已经搜索过，应该从搜索区间中去除。此算法有什么缺陷？答：至此，你应该已经掌握了该算法的所有细节，以及这样处理的原因。但是，这个算法存在局限性。比如说给你有序数组 nums = [1,2,2,2,3]，target = 2，此算法返回的索引是
2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引
3，这样的话此算法是无法处理的。这样的需求很常见。
你也许会说，找到一个 target，然后向左或向右线性搜索不行吗？可以，但是不好，因为这样难以保证二分查找对数级的复杂度了。我们后续的算法就来讨论这两种二分查找的算法。
二、寻找左侧边界的二分搜索直接看代码，其中的标记是需要注意的细节：

   '''c
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0;
int right = nums.length; // 注意
   while (left < right) { // 注意
    int mid = (left + right) / 2;
    if (nums[mid] == target) {
        right = mid;
    } else if (nums[mid] < target) {
        left = mid + 1;
    } else if (nums[mid] > target) {
        right = mid; // 注意
    }
}
return left;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

}为什么 while(left < right) 而不是 <= ?
答：用相同的方法分析，因为 right = nums.length 而不是 nums.length - 1 。因此每次循环的「搜索区间」是 [left, right) 左闭右开。while(left < right) 终止的条件是 left == right，此时搜索区间 [left, left) 为空，所以可以正确终止
2. 为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？
答：因为要一步一步来，先理解一下这个「左侧边界」有什么特殊含义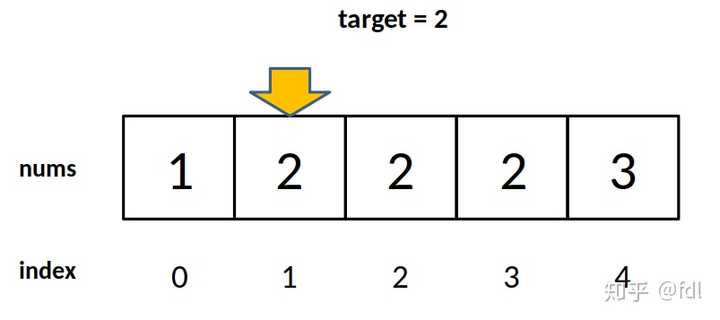：对于这个数组，算法会返回 1。这个 1 的含义可以这样解读：nums 中小于 2 的元素有 1 个。比如对于有序数组 nums = [2,3,5,7], target = 1，算法会返回 0，含义是：nums 中小于 1 的元素有 0 个。再比如说 nums 不变，target = 8，算法会返回 4，含义是：nums 中小于 8 的元素有 4 个。综上可以看出，函数的返回值（即 left 变量的值）取值区间是闭区间 [0, nums.length]，所以我们简单添加两行代码就能在正确的时候 return -1：while (left < right) {
//…
}
// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;
3. 为什么 left = mid + 1，right = mid ？和之前的算法不一样？答：这个很好解释，因为我们的「搜索区间」是 [left, right) 左闭右开，所以当 nums[mid] 被检测之后，下一步的搜索区间应该去掉 mid 分割成两个区间，即 [left, mid) 或 [mid + 1, right)。
4. 为什么该算法能够搜索左侧边界？
答：关键在于对于 nums[mid] == target 这种情况的处理：if (nums[mid] == target)
right = mid;可见，找到 target 时不要立即返回，而是缩小「搜索区间」的上界 right，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。
5. 为什么返回 left 而不是 right？答：都是一样的，因为 while 终止的条件是 left == right。三、寻找右侧边界的二分查找寻找右侧边界和寻找左侧边界的代码差不多，只有两处不同，已标注：

   '''c
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
   while (left < right) {
    int mid = (left + right) / 2;
    if (nums[mid] == target) {
        left = mid + 1; // 注意
    } else if (nums[mid] < target) {
        left = mid + 1;
    } else if (nums[mid] > target) {
        right = mid;
    }
}
return left - 1; // 注意
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

}为什么这个算法能够找到右侧边界？答：类似地，关键点还是这里：if (nums[mid] == target) {
left = mid + 1;当 nums[mid] == target 时，不要立即返回，而是增大「搜索区间」的下界 left，使得区间不断向右收缩，达到锁定右侧边界的目的。2. 为什么最后返回 left - 1 而不像左侧边界的函数，返回 left？而且我觉得这里既然是搜索右侧边界，应该返回 right 才对。答：首先，while 循环的终止条件是 left == right，所以 left 和 right 是一样的，你非要体现右侧的特点，返回 right - 1 好了。至于为什么要减一，这是搜索右侧边界的一个特殊点，关键在这个条件判断：if (nums[mid] == target) {
left = mid + 1;
// 这样想: mid = left - 1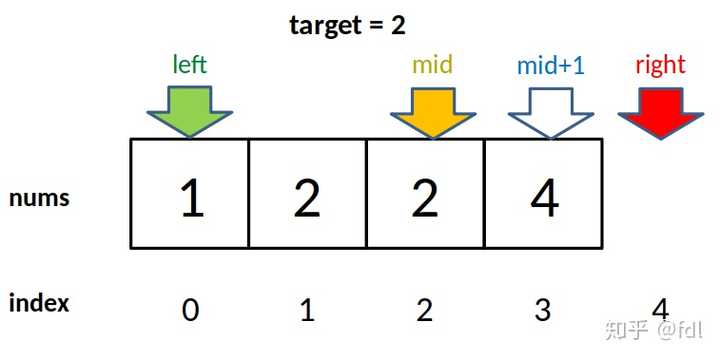因为我们对 left 的更新必须是 left = mid + 1，就是说 while 循环结束时，nums[left] 一定不等于 target 了，而 nums[left-1] 可能是 target。至于为什么 left 的更新必须是 left = mid + 1，同左侧边界搜索，就不再赘述。3. 为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？答：类似之前的左侧边界搜索，因为 while 的终止条件是 left == right，就是说 left 的取值范围是 [0, nums.length]，所以可以添加两行代码，正确地返回 -1：while (left < right) {
// …
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;四、最后总结来梳理一下这些细节差异的因果逻辑：第一个，最基本的二分查找算法：因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1

因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回第二个，寻找左侧边界的二分查找：因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid

因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界第三个，寻找右侧边界的二分查找：因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid

因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界

又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right，必须减一如果以上内容你都能理解，那么恭喜你，二分查找算法的细节不过如此。通过本文，你学会了： 分析二分查找代码时，不要出现 else，全部展开成 else if 方便理解。 注意「搜索区间」和 while 的终止条件，如果存在漏掉的元素，记得在最后检查。 如需要搜索左右边界，只要在 nums[mid] == target 时做修改即可。搜索右侧时需要减一。就算遇到其他的二分查找变形，运用这几点技巧，也能保证你写出正确的代码。LeetCode Explore 中有二分查找的专项练习，其中提供了三种不同的代码模板，现在你再去看看，很容易就知道这几个模板的实现原理了。欢迎关注我的公众号 labuladong，致力于把算法问题讲清楚～