归并排序详解（递归与非递归）

归并排序是建立在归并操作上的一种有效算法。该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列间断有序。若将两个有序表合并成一个有序表，成为二路归并。

一、递归实现归并排序

1.算法描述

● 把长度为n的输入序列分成两个长度近似为n/2（[begin,mid]  [mid + 1,end] ）的子序列

● 对这两个子序列再分别进行归并排序，将区间分解到不可在分为止

● 依次将两个排序好的子序列合并成一个最终的排序序列 

方法： 开辟新数组，用双指针选出两个子序列中的较小元素尾插在新数组中

 2.动图演示

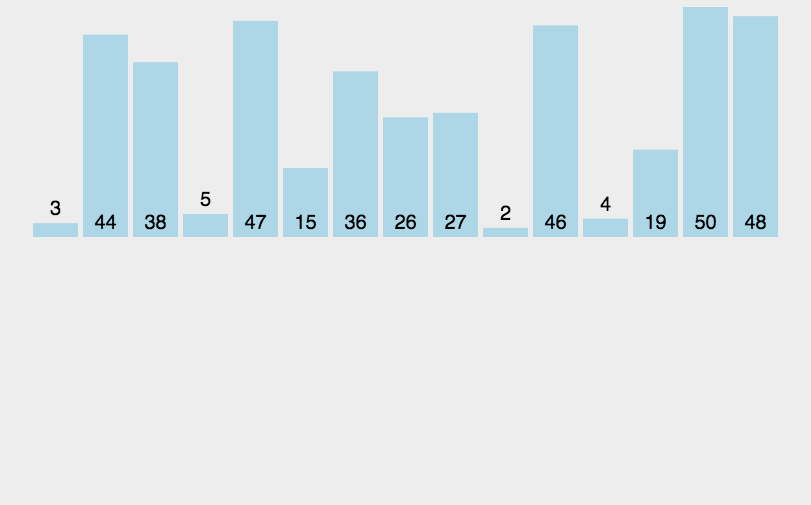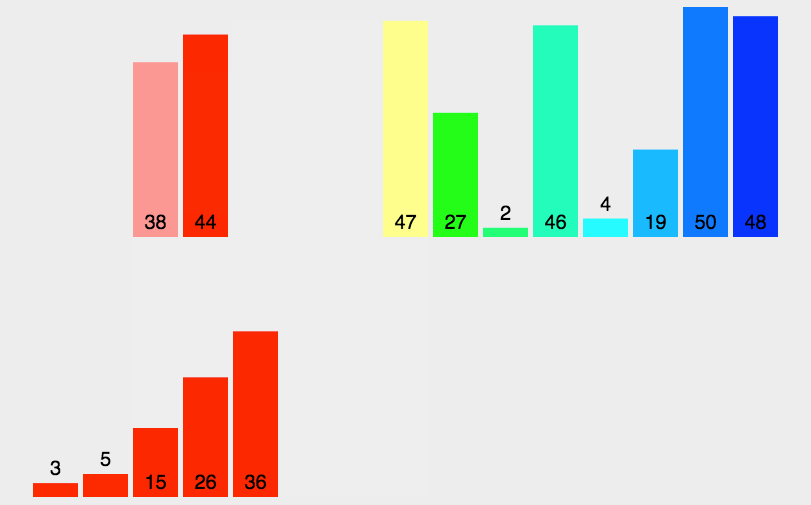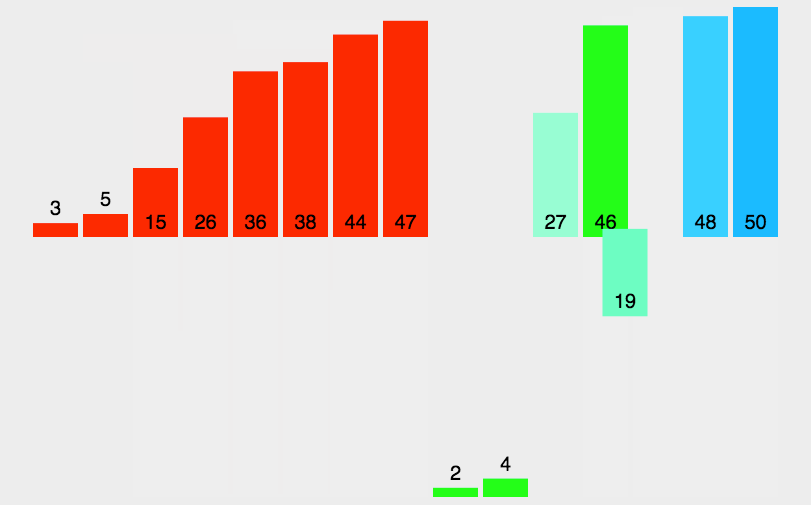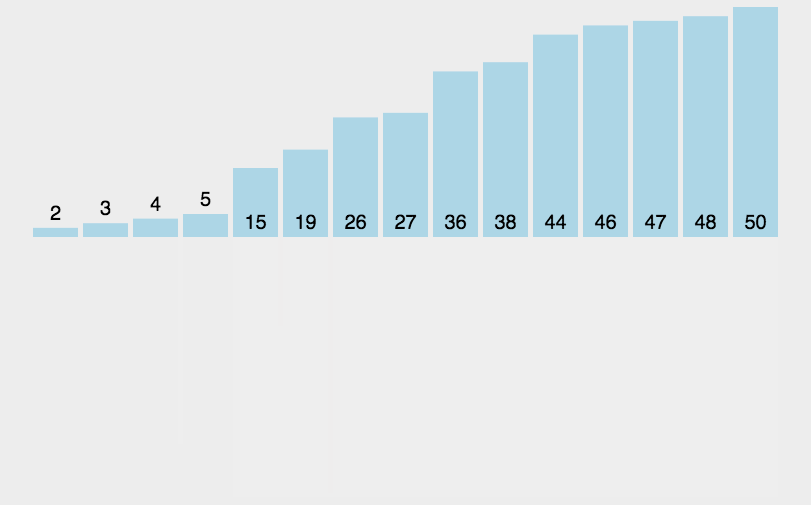
3.核心步骤 

(1)图示

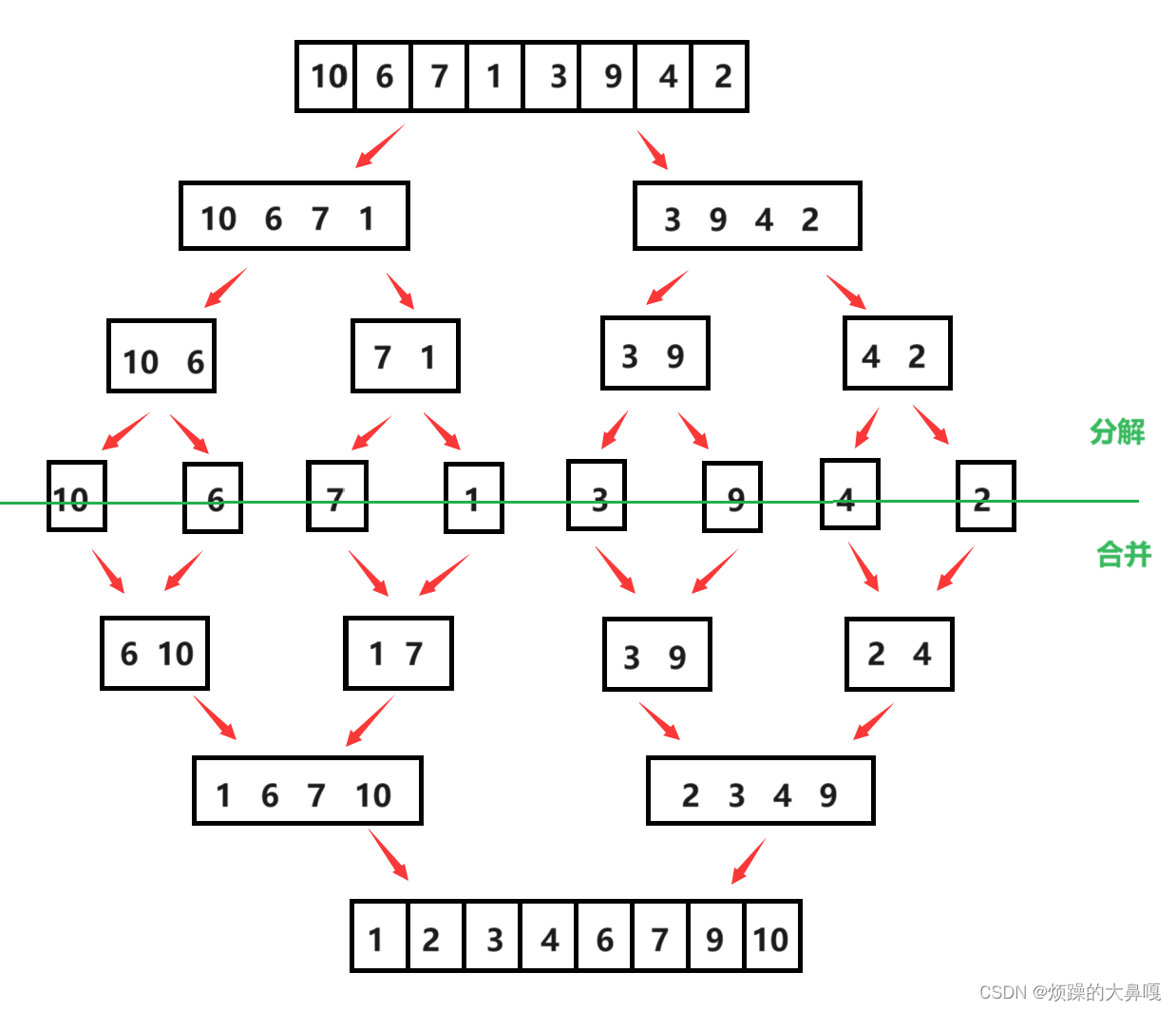
(2)思考

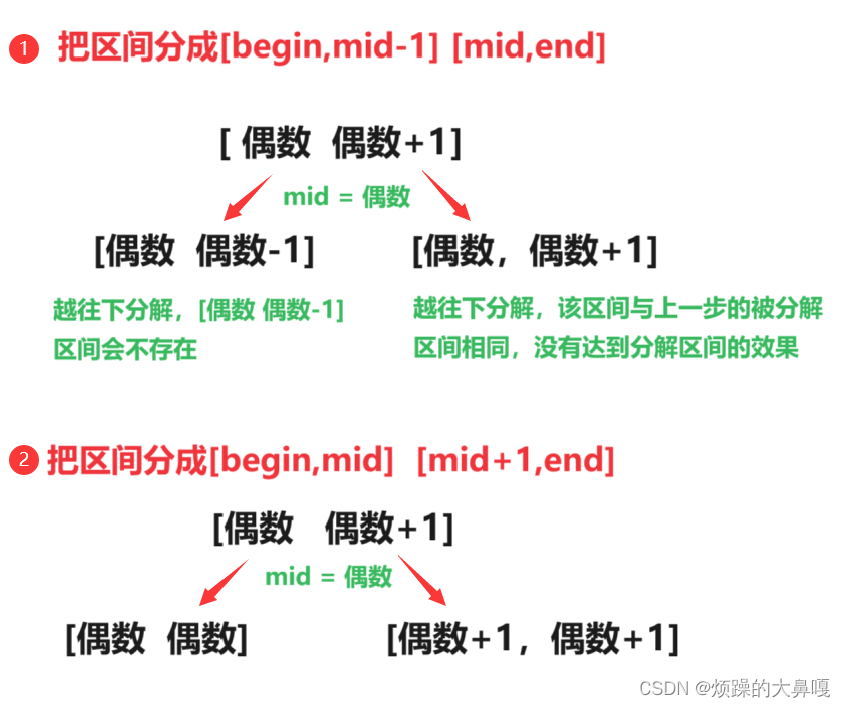
为什么要将区间拆分成[begin,mid]  [mid + 1,end] ?

上面介绍过我们的算法步骤是把长度为 n 的输入序列分成两个长度近似为 n/2 的子序列，在此前提下，除了分成[begin,mid]  [mid + 1,end]外，还有一种分法：[begin,mid-1] [mid,end]，为什么不用这种分法？

mid = (begin + end)/2，所以mid是偶数

示例：用两种不同的分法分解区间[0,9]

当所要分解的区间是 [偶数，偶数]，上述的两种分法都行得通，但是当区间是[偶数，偶数+1]的情况，[begin,mid-1] [mid,end]这种分法就行不通。

5.参考代码

void _MergeSort(int* arr, int* tmp, int begin, int end)
{
	if (begin >= end)
		return;
 
	int mid = (begin + end) / 2;//偶数
	//[begin,mid]  [mid+1,end] ——>[偶数，偶数] [偶数+1，偶数+1]
	_MergeSort(arr,tmp, begin, mid);
	_MergeSort(arr, tmp, mid + 1, end);
	
	//左右区间有序就可以归并了
	//归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] < arr[begin2])
		{
			tmp[i++] = arr[begin1++];
		}
		else
		{
			tmp[i++] = arr[begin2++];
		}
	}
	//剩下的尾插在tmp数组
	while (begin1 <= end1)
	{
		tmp[i++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = arr[begin2++];
	}
	//将一定长度的tmp复制到arr中
	memcpy(arr + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
//归并
void MergeSort(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail!");
		return;
	}
	_MergeSort(arr,tmp, 0, n - 1);
 
	free(tmp);
	tmp = NULL;
}

不同排序对一百万个随机数进行排序的效率： （毫秒）

二、非递归实现归并排序

1.算法描述

● gap表示每组归并的数据个数

● i 表示每组归并的起始位置

● 两层循环，一层循环用来归并数组中的数据，另一层扩大归并的数据个数

2.核心步骤

(1)图示

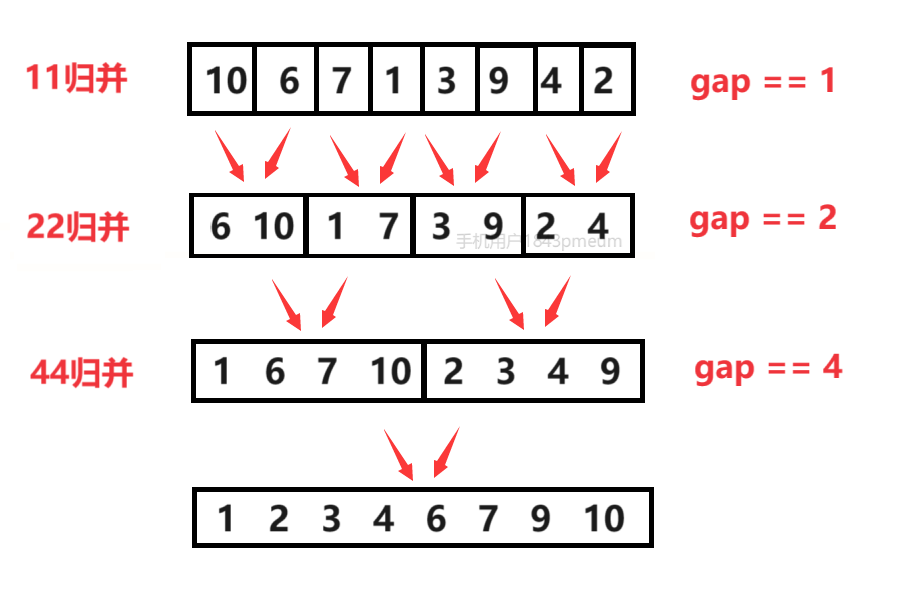
 (2)思考

为什么要归并一次拷贝一次？

● 如果整体拷贝，在上述的“第二组的都越界不存在”的情况下，虽然跳出循环,但在整体拷贝的时候还会把越界的部分拷贝回去

● 但如果归并一次拷贝一次，在“第二组的都越界不存在”的情况下，直接跳出循环，不会将越界的部分拷贝到数组中

3.参考代码 

//归并（非递归）
void MergeSortNonR(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail!");
		return;
	}
	//gap表示每组要归并数据的个数
	int gap = 1;
	while (gap  < n)
	{    //i表示每组归并的起始位置
		for (int i = 0; i < n; i += 2 * gap)//个数于区间的转化关系
		{//[bagin1,end1] [bagin2,end2]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
 
			//第二组的都越界不存在，那么第二组不用归并了，跳出循环
			if (begin2 > n)
				break;
 
			//第二组的begin2没越界，end2越界了，需要修正区间，再归并
			if (end2 > n)
				end2 = n - 1;
 
			//归并
			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (arr[begin1] < arr[begin2])
				{
					tmp[j++] = arr[begin1++];
				}
				else
				{
					tmp[j++] = arr[begin2++];
				}
			}
			//剩下的尾插在tmp数组
			while (begin1 <= end1)
			{
				tmp[j++] = arr[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = arr[begin2++];
			}
			//将一定长度的tmp复制到arr中
            //归并一次拷贝一次
			memcpy(arr + i, tmp + i, (end2 - i + 1) * sizeof(int));
		}
		gap *= 2;
	}
	free(tmp);
	tmp = NULL;
}

三、算法分析 

归并排序是一种稳定的排序方法。和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是，代价是需要额外的内存空间。

特性总结：

(1) 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在此版中的外排序问题

(2) 时间复杂度：O(N*logN)  相当于一个满二叉树

(3) 空间复杂度：O(N)  开辟了一个额外的数组

(4) 稳定性：稳定