devbox
盐析白兔
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

三维重建-单目相机标定_单目相机三维重建代码

作者：盐析白兔 | 2024-02-22 01:05:28

赞

踩

单目相机三维重建代码

文章目录

文章目录

前言

一、代码讲解

1、SingleCamera

2、SingleCamera::compose()

3、SingleCamera::svdP()

4、SingleCamera::workIntrinsicAndExtrinsic()

5、SingleCamera::selfcheck

二、完整代码

三、 Cmake配置

总结

前言

        理论知识可以看北邮鲁鹏老师的课程，哔哩哔哩上有。

一、代码讲解

1、SingleCamera

  1. class SingleCamera {
  2. public:
  3.     // 构造函数，初始化成员变量
  4.     SingleCamera(Eigen::MatrixXf world_coor, Eigen::MatrixXf pixel_coor, int n)
  5.             : world_coor(world_coor), pixel_coor(pixel_coor), point_num(n),
  6.               P(Eigen::MatrixXf::Zero(2 * n, 12)), M(Eigen::MatrixXf::Zero(3, 4)),
  7.               A(Eigen::MatrixXf::Zero(3, 3)), b(Eigen::MatrixXf::Zero(3, 1)),
  8.               K(Eigen::MatrixXf::Zero(3, 3)), R(Eigen::MatrixXf::Zero(3, 3)),
  9.               t(Eigen::MatrixXf::Zero(3, 1)) {}
  10.  
  11.     // 用像素坐标和世界坐标计算相机矩阵 P
  12.     void composeP();
  13.  
  14.     // 对相机矩阵 P 进行奇异值分解，计算相机内部矩阵 A 和外部矩阵 M
  15.     void svdP();
  16.  
  17.     // 计算相机的内部和外部参数
  18.     void workIntrinsicAndExtrinsic();
  19.  
  20.     // 对标定结果进行自检
  21.     void selfcheck(const Eigen::MatrixXf &w_check, const Eigen::MatrixXf &c_check);
  22.  
  23. private:
  24.     // 成员变量，存储世界坐标和像素坐标以及相关矩阵
  25.     Eigen::MatrixXf world_coor;
  26.     Eigen::MatrixXf pixel_coor;
  27.     int point_num;
  28.     Eigen::MatrixXf P;
  29.     Eigen::MatrixXf M;
  30.     Eigen::MatrixXf A;
  31.     Eigen::MatrixXf b;
  32.     Eigen::MatrixXf K;
  33.     Eigen::MatrixXf R;
  34.     Eigen::MatrixXf t;
  35. };

        类SingleCamera实现了与相机标定和 3D 重建相关的功能。该类具有几个成员变量和函数：

成员变量：

  • world_coor：一个 Eigen::MatrixXf 矩阵，表示世界坐标系中点的 3D 坐标。

  • pixel_coor：一个 Eigen::MatrixXf 矩阵，表示相应点在相机图像平面上的 2D 坐标。

  • point_num：一个整数，表示点的数量。

  • P：一个大小为 2n x 12 的 Eigen::MatrixXf 矩阵，其中 n 是点的数量。该矩阵用于表示相机矩阵。

  • M：一个大小为 3 x 4 的 Eigen::MatrixXf 矩阵，表示相机矩阵形式为 [R|t]。

  • A：一个大小为 3 x 3 的 Eigen::MatrixXf 矩阵，表示相机的内部矩阵。

  • b：一个大小为 3 x 1 的 Eigen::MatrixXf 矩阵，表示相机的平移向量。

  • K：一个大小为 3 x 3 的 Eigen::MatrixXf 矩阵，表示相机的校准矩阵。

2、SingleCamera::compose()

  1.  
  2. void SingleCamera::compose() {
  3.  根据输入的二维点和三维点，构造P矩阵
  4. Eigen::RowVectorXf row(12), p(4);
  5. float u, v;
  6. int p_idx = 0;
  7. for (int i = 0; i < point_num; i++) {
  8. // 一次生成两个方程系数，用于构造P矩阵
  9. p = world_coor.row(i);
  10. u = pixel_coor(i, 0);
  11. v = pixel_coor(i, 1);
  12. row << p, // 第一行：三维点
  13. Eigen::RowVectorXf::Zero(1, 4), // 第一行：第二个四维0向量
  14. -u * p; // 第一行：负的像素坐标x值乘以三维点坐标
  15. P.row(p_idx++) = row; // 将该行加入P矩阵中，并将行索引值加1
  16. row << Eigen::RowVectorXf::Zero(1, 4), // 第二行：第一个四维0向量
  17. p, // 第二行：三维点
  18. -v * p; // 第二行：负的像素坐标y值乘以三维点坐标
  19. P.row(p_idx++) = row; // 将该行加入P矩阵中，并将行索引值加1
  20. }
  21.  
  22. std::cout << "P:\n" << P << std::endl;
  23.  
  24. }

        其中的 composeP 函数用于生成 P 矩阵。在计算机视觉中，P 矩阵是一个 3x4 的矩阵，它包含了相机的内参、外参以及相机的位置和姿态等信息，可以用于将三维世界坐标系中的点映射到二维像素坐标系中。

        具体地，该函数根据输入的二维点 pixel_coor 和三维点 world_coor，构造 P 矩阵。在生成 P 矩阵的过程中，对于每一个三维点，通过将其与对应的二维点组合构造两个方程式，从而构成一个 2x12 的子矩阵，最后将所有子矩阵组合成一个 2n x 12 的 P 矩阵。其中，n 表示输入的点的数量。

        具体实现过程是，在 for 循环中，首先从 world_coor 中取出当前点的三维坐标，然后将其与对应的二维点 pixel_coor(i, 0) 和 pixel_coor(i, 1) 组合，构造出一个 2x1 的向量。接着，在构造 2x12 的子矩阵时，将该向量与一些零元素组合成一个 1x12 的行向量，然后再将该行向量作为子矩阵的第一行，构造出一个 2x12 的子矩阵。具体地，子矩阵的第一行为 [X, Y, Z, 1, 0, 0, 0, 0, -uX, -uY, -uZ, -u]，其中 X、Y、Z 分别表示当前点的三维坐标，u 表示当前点的横坐标 pixel_coor(i, 0)。接下来，将该子矩阵加入到 P 矩阵中。然后，再以类似的方式构造出一个第二行为 [0, 0, 0, 0, X, Y, Z, 1, -vX, -vY, -vZ, -v] 的子矩阵，并将其也加入到 P 矩阵中。最终生成的 P 矩阵的大小为 2n x 12。

        需要注意的是，该函数并没有对 P 矩阵进行求解，它只是将输入的点转化为 P 矩阵的形式。P 矩阵的求解需要使用其他方法，例如使用 SVD 分解或者直接进行线性求解等。

3、SingleCamera::svdP()

  1. void SingleCamera::svdP() {
  2.     // homework2: 根据P矩阵求解M矩阵和A、b矩阵
  3.  
  4.     // 使用JacobiSVD求解P矩阵的奇异值分解
  5.     Eigen::JacobiSVD<Eigen::MatrixXf> svd;
  6.     svd.compute(P, Eigen::ComputeThinU | Eigen::ComputeThinV);
  7.  
  8.     // 取出V矩阵的最后一列并重构成4x3矩阵，得到M矩阵
  9.     M = svd.matrixV().col(svd.matrixV().cols() - 1);
  10.     M.resize(4, 3);
  11.     M.transposeInPlace();
  12.  
  13.     // 将M矩阵分解为A和b矩阵
  14.     A = M.leftCols(3);   // 3x3的A矩阵
  15.     b = M.rightCols(1);  // 3x1的b矩阵
  16. }

      通过输入的二维像素点和对应的三维世界坐标点，求解相机的姿态矩阵。通过对之前构造的P矩阵进行奇异值分解（SVD），得到M矩阵，并将其拆分成A矩阵和b向量的形式。其中M矩阵的最后一列是一个齐次坐标，所以取矩阵V中的最后一列作为M矩阵，并将其resize为4x3的形式。最后通过对M矩阵的拆分得到A矩阵和b向量，A矩阵是一个3x3的矩阵，代表了相机内参，b向量是一个3x1的向量，代表了相机的平移向量。

4、SingleCamera::workIntrinsicAndExtrinsic()

  1. void SingleCamera::workIntrinsicAndExtrinsic() {
  2.     // homework3: 求解相机的内参和外参
  3.     Eigen::RowVector3f a1(A.row(0)), a2(A.row(1)), a3(A.row(2));  // 将A矩阵的前三行分别作为a1, a2, a3
  4.  
  5.     auto roh = -1 / a3.norm();  // 计算rho，为a3的模长的倒数的相反数
  6.  
  7.     auto cx = roh * roh * (a1.dot(a3));  // 计算cx
  8.     auto cy = roh * roh * (a2.dot(a3));  // 计算cy
  9.  
  10.     auto a1xa3 = a1.cross(a3);  // 计算向量a1和a3的叉积
  11.     auto a2xa3 = a2.cross(a3);  // 计算向量a2和a3的叉积
  12.     auto cos_theta = -1 * a1xa3.dot(a2xa3) / (a1xa3.norm() * a2xa3.norm());  // 计算cos(theta)，即向量a1xa3和a2xa3的点积除以模长的积的相反数
  13.     auto sin_theta = sqrt(1 - cos_theta * cos_theta);  // 计算sin(theta)
  14.  
  15.     auto alpha = roh * roh * a1xa3.norm() * sin_theta;  // 计算alpha
  16.     auto beta = roh * roh * a2xa3.norm() * sin_theta;   // 计算beta
  17.  
  18.     auto r1 = 1 * a2xa3 / a2xa3.norm();  // 计算向量r1
  19.     auto r2 = -r1 * cos_theta / sin_theta - (roh * roh) / alpha * a1xa3;  // 计算向量r2
  20.     auto r3 = r1.cross(r2);  // 计算向量r3
  21.  
  22.     // calculate the sign of roh
  23.     auto rohs = r3.array() / a3.array();  // 将r3的每个元素都除以a3对应的元素
  24.     if (rohs[0] > 0) {  // 如果r3的第一个元素大于0
  25.         roh *= -1;  // 取rho的相反数
  26.     }
  27.  
  28.     K(0, 0) = alpha;  // 将alpha赋值给K矩阵的(0,0)位置
  29.     K(0, 1) = -alpha * cos_theta / sin_theta;  // 将alpha, cos(theta), sin(theta)计算出的值赋给K矩阵的(0,1)位置
  30.     K(0, 2) = cx;  // 将cx赋值给K矩阵的(0,2)位置
  31.     K(1, 1) = beta / sin_theta;  // 将beta, sin(theta)计算出的值赋给K矩阵的(1,1)位置
  32.     K(1, 2) = cy;  // 将cy赋值给K矩阵的(1,2)位置
  33.     K(2, 2) = 1;
  34.     R.row(0) = r1;
  35.     R.row(1) = r2;
  36.     R.row(2) = r3;
  37.     t = roh * K.inverse() * b;
  38.  
  39.     std::cout << "K is " << std::endl << K << std::endl;
  40.     std::cout << "R is " << std::endl << R << std::endl;
  41.     std::cout << "t is " << std::endl << t.transpose() << std::endl;
  42. }

        在 workIntrinsicAndExtrinsic() 函数中，首先提取矩阵 A 的三行，并根据 A 矩阵的特征推导相机内参，包括焦距（alpha 和 beta）、图像中心的位置（cx 和 cy）和像素间距的尺度因子（roh）。

接下来，根据 A 矩阵推导出的旋转矩阵的第一列 r1，使用旋转矩阵的正交性质推导出 r2 和 r3。

最后，根据推导出的相机内参和外参，计算相机的平移向量 t。

代码的最后，输出相机内参矩阵 K、旋转矩阵 R 和平移向量 t。

5、SingleCamera::selfcheck

  1. // 传入测试点w_check和对应的像素坐标c_check，计算误差
  2. void SingleCamera::selfcheck(const Eigen::MatrixXf &w_check, const Eigen::MatrixXf &c_check) {
  3. float average_err = DBL_MAX;// 将R、t拼接成M矩阵，再用相机内参矩阵K相乘得到投影矩阵P，然后将测试点w_check通过投影矩阵P投影到像素坐标系下
  4. Eigen::MatrixXf m(3, 4);
  5. m << R, t;
  6. auto trans_xyz = w_check * (K * m).transpose();
  7.  
  8. // 逐个计算每个像素坐标的误差
  9. for (int i = 0; i < c_check.rows(); ++i) {
  10.     if (i == 0) average_err = 0;
  11.  
  12.     // 计算投影后的点在像素坐标系下的坐标值
  13.     auto trans_z = trans_xyz(i, 2);
  14.     auto trans_x = trans_xyz(i, 0) / trans_z;
  15.     auto trans_y = trans_xyz(i, 1) / trans_z;
  16.  
  17.     // 计算投影后的点和对应测试点的误差，并将误差累加
  18.     average_err += abs(trans_x - c_check(i, 0));
  19.     average_err += abs(trans_y - c_check(i, 1));
  20. }
  21.  
  22. // 计算平均误差
  23. average_err /= c_check.size();
  24.  
  25. // 输出结果
  26. std::cout << "The average error is " << average_err << "," << std::endl;
  27. if (average_err > 0.1) {
  28.     std::cout << "which is more than 0.1" << std::endl;
  29. } else {
  30.     std::cout << "which is smaller than 0.1, the M is acceptable" << std::endl;
  31. }

        用于对相机参数进行自检。输入是两个矩阵w_check和c_check，分别表示世界坐标系下的点和相机图像平面上对应的点。函数的作用是利用之前通过作业3求解得到的相机参数，计算这些参数对给定的测试点的投影误差，判断相机参数的有效性。具体实现过程如下：

首先，通过将旋转和平移向量组合成一个3x4的矩阵，构造一个包含所有相机参数的矩阵m。然后，将这个矩阵与内部矩阵K相乘，得到一个3x3的投影矩阵P，再将其与世界坐标系下的点w_check相乘，得到一个3xN的齐次坐标矩阵trans_xyz，其中N表示测试点的数量。

接下来，对于每一个测试点，通过齐次坐标矩阵中对应的第i行，计算出点的三维坐标。具体来说，先将trans_xyz中第i行的第三个元素作为点的Z坐标，然后将其它两个元素分别除以这个Z坐标，得到点在相机坐标系下的X和Y坐标。这些坐标可以通过在内部矩阵K中乘以它们来得到对应的像素坐标。

最后，通过计算每个测试点的投影误差，得到所有测试点的平均误差。如果这个平均误差大于0.1，则认为相机参数不够精确，否则认为参数有效。函数将输出平均误差以及相机参数是否有效的信息。

二、完整代码

  1. #include <iostream>
  2. #include <vector>
  3. #include <cmath>
  4. #include <cfloat>
  5. #include <eigen3/Eigen/Dense>
  6. #include <eigen3/Eigen/SVD>
  7.  
  8. class SingleCamera {
  9. public:
  10.     SingleCamera(Eigen::MatrixXf world_coor, Eigen::MatrixXf pixel_coor, int n)
  11.             : world_coor(world_coor), pixel_coor(pixel_coor), point_num(n),
  12.               P(Eigen::MatrixXf::Zero(2 * n, 12)), M(Eigen::MatrixXf::Zero(3, 4)),
  13.               A(Eigen::MatrixXf::Zero(3, 3)), b(Eigen::MatrixXf::Zero(3, 1)),
  14.               K(Eigen::MatrixXf::Zero(3, 3)), R(Eigen::MatrixXf::Zero(3, 3)),
  15.               t(Eigen::MatrixXf::Zero(3, 1)) {}
  16.  
  17.     void composeP();
  18.  
  19.     void svdP();
  20.  
  21.     void workIntrinsicAndExtrinsic();
  22.  
  23.     void selfcheck(const Eigen::MatrixXf &w_check, const Eigen::MatrixXf &c_check);
  24.  
  25. private:
  26.     Eigen::MatrixXf world_coor;
  27.     Eigen::MatrixXf pixel_coor;
  28.     int point_num;
  29.  
  30.     // 变量都是与课程PPT相对应的
  31.     Eigen::MatrixXf P;
  32.     Eigen::MatrixXf M;
  33.     Eigen::MatrixXf A;
  34.     Eigen::MatrixXf b;
  35.     Eigen::MatrixXf K;
  36.     Eigen::MatrixXf R;
  37.     Eigen::MatrixXf t;
  38. };
  39.  
  40. void SingleCamera::composeP() {
  41.     // homework1: 根据输入的二维点和三维点，构造P矩阵
  42.     Eigen::RowVectorXf row(12), p(4);
  43.     float u, v;
  44.     int p_idx = 0;
  45.     for (int i = 0; i < point_num; i++) {
  46.         // 一次生成两个方程系数
  47.         p = world_coor.row(i);
  48.         u = pixel_coor(i, 0);
  49.         v = pixel_coor(i, 1);
  50.         row << p,
  51.                 Eigen::RowVectorXf::Zero(1, 4),
  52.                 -u * p;
  53.         P.row(p_idx++) = row;
  54.         row << Eigen::RowVectorXf::Zero(1, 4),
  55.                 p,
  56.                 -v * p;
  57.         P.row(p_idx++) = row;
  58.     }
  59.  
  60. //    std::cout << "P:\n" << P << std::endl;
  61.  
  62. }
  63.  
  64. void SingleCamera::svdP() {
  65.     // homework2: 根据P矩阵求解M矩阵和A、b矩阵
  66.     Eigen::JacobiSVD<Eigen::MatrixXf> svd;
  67.     svd.compute(P, Eigen::ComputeThinU | Eigen::ComputeThinV);
  68.     M = svd.matrixV().col(svd.matrixV().cols() - 1);
  69.     M.resize(4, 3);
  70.     M.transposeInPlace();
  71.     A = M.leftCols(3);   //[3, 3]
  72.     b = M.rightCols(1);  //[3, 1]
  73. }
  74.  
  75. void SingleCamera::workIntrinsicAndExtrinsic() {
  76.     // homework3: 求解相机的内参和外参
  77.     Eigen::RowVector3f a1(A.row(0)), a2(A.row(1)), a3(A.row(2));
  78.  
  79.     auto roh = -1 / a3.norm();
  80.  
  81.     auto cx = roh * roh * (a1.dot(a3));
  82.     auto cy = roh * roh * (a2.dot(a3));
  83.  
  84.     auto a1xa3 = a1.cross(a3);
  85.     auto a2xa3 = a2.cross(a3);
  86.     auto cos_theta = -1 * a1xa3.dot(a2xa3) / (a1xa3.norm() * a2xa3.norm());
  87.     auto sin_theta = sqrt(1 - cos_theta * cos_theta);
  88.  
  89.     auto alpha = roh * roh * a1xa3.norm() * sin_theta;
  90.     auto beta = roh * roh * a2xa3.norm() * sin_theta;
  91.  
  92. //    auto r1 = a2xa3 / a2xa3.norm();
  93. //    auto r3 = a3 / a3.norm();
  94. //    auto r2 = r3.cross(r1);
  95.     auto r1 = 1 * a2xa3 / a2xa3.norm();
  96.     auto r2 = -r1 * cos_theta / sin_theta - (roh * roh) / alpha * a1xa3;
  97.     auto r3 = r1.cross(r2);
  98.     // calculate the sign of roh
  99.     auto rohs = r3.array() / a3.array();
  100.     if (rohs[0] > 0) {
  101.         roh *= -1;
  102.     }
  103.  
  104.     K(0, 0) = alpha;
  105.     K(0, 1) = -alpha * cos_theta / sin_theta;
  106.     K(0, 2) = cx;
  107.     K(1, 1) = beta / sin_theta;
  108.     K(1, 2) = cy;
  109.     K(2, 2) = 1;
  110.     R.row(0) = r1;
  111.     R.row(1) = r2;
  112.     R.row(2) = r3;
  113.     t = roh * K.inverse() * b;
  114.  
  115.     std::cout << "K is " << std::endl << K << std::endl;
  116.     std::cout << "R is " << std::endl << R << std::endl;
  117.     std::cout << "t is " << std::endl << t.transpose() << std::endl;
  118. }
  119.  
  120. void SingleCamera::selfcheck(const Eigen::MatrixXf &w_check, const Eigen::MatrixXf &c_check) {
  121.     float average_err = DBL_MAX;
  122.     // homework4: 根据homework3求解得到的相机的参数，使用测试点进行验证，计算误差
  123.     Eigen::MatrixXf m(3, 4);
  124.     m << R, t;
  125.  
  126.     auto trans_xyz = w_check * (K * m).transpose();
  127.  
  128.     for (int i = 0; i < c_check.rows(); ++i) {
  129.         if (i == 0) average_err = 0;
  130.         auto trans_z = trans_xyz(i, 2);
  131.         auto trans_x = trans_xyz(i, 0) / trans_z;
  132.         auto trans_y = trans_xyz(i, 1) / trans_z;
  133.         average_err += abs(trans_x - c_check(i, 0));
  134.         average_err += abs(trans_y - c_check(i, 1));
  135.     }
  136.     average_err /= c_check.size();
  137.  
  138.     std::cout << "The average error is " << average_err << "," << std::endl;
  139.     if (average_err > 0.1) {
  140.         std::cout << "which is more than 0.1" << std::endl;
  141.     } else {
  142.         std::cout << "which is smaller than 0.1, the M is acceptable" << std::endl;
  143.     }
  144. }
  145.  
  146. int main(int argc, char **argv) {
  147. // 三维世界坐标系中的点
  148. Eigen::MatrixXf w_xz(4, 4);
  149. w_xz << 8, 0, 9, 1,
  150.         8, 0, 1, 1,
  151.         6, 0, 1, 1,
  152.         6, 0, 9, 1;
  153.  
  154. Eigen::MatrixXf w_xy(4, 4);
  155. w_xy << 5, 1, 0, 1,
  156.         5, 9, 0, 1,
  157.         4, 9, 0, 1,
  158.         4, 1, 0, 1;
  159.  
  160. Eigen::MatrixXf w_yz(4, 4);
  161. w_yz << 0, 4, 7, 1,
  162.         0, 4, 3, 1,
  163.         0, 8, 3, 1,
  164.         0, 8, 7, 1;
  165.  
  166. // 三维世界坐标系中的所有点
  167. Eigen::MatrixXf w_coor(12, 4);
  168. w_coor << w_xz,
  169.         w_xy,
  170.         w_yz;
  171.  
  172. // 对应的图像坐标系中的点
  173. Eigen::MatrixXf c_xz(4, 2);
  174. c_xz << 275, 142,
  175.         312, 454,
  176.         382, 436,
  177.         357, 134;
  178.  
  179. Eigen::MatrixXf c_xy(4, 2);
  180. c_xy << 432, 473,
  181.         612, 623,
  182.         647, 606,
  183.         464, 465;
  184.  
  185. Eigen::MatrixXf c_yz(4, 2);
  186. c_yz << 654, 216,
  187.         644, 368,
  188.         761, 420,
  189.         781, 246;
  190.  
  191. // 对应的图像坐标系中的所有点
  192. Eigen::MatrixXf c_coor(12, 2);
  193. c_coor << c_xz,
  194.         c_xy,
  195.         c_yz;
  196.  
  197. // 定义SingleCamera对象，传入三维世界坐标系中所有点和对应的图像坐标系中的点，共使用12个点
  198. SingleCamera aCamera = SingleCamera(w_coor, c_coor, 12);
  199.  
  200. aCamera.composeP();  // 用所有点求解P矩阵
  201. aCamera.svdP();      // 对P矩阵进行奇异值分解
  202. aCamera.workIntrinsicAndExtrinsic();  // 求解相机的内外参数
  203.  
  204. // 使用测试点进行验证，计算误差
  205. Eigen::MatrixXf w_check(5, 4);
  206. w_check << 6, 0, 5, 1,
  207.         3, 3, 0, 1,
  208.         0, 4, 0, 1,
  209.         0, 4, 4, 1,
  210.         0, 0, 7, 1;
  211.  
  212. Eigen::MatrixXf c_check(5, 2);
  213. c_check << 369, 297,
  214.             531, 484,
  215.             640, 468,
  216.             646, 333,
  217.             556, 194;
  218.  
  219.     SingleCamera aCamera = SingleCamera(w_coor, c_coor, 12);  // 12 points in total are used
  220.     aCamera.composeP();
  221.     aCamera.svdP();
  222.     aCamera.workIntrinsicAndExtrinsic();
  223.     aCamera.selfcheck(w_check, c_check);  // test 5 points and verify M
  224.  
  225.  
  226.     return 0;
  227. }

三、 Cmake配置

  1. cmake_minimum_required(VERSION 3.10)
  2.  
  3.  
  4. set(CMAKE_BUILD_TYPE release)
  5. set(CMAKE_CXX_FLAGS_RELEASE "-O3 -fPIC")
  6. set(CMAKE_MODULE_PATH ${CMAKE_MODULE_PATH} "${CMAKE_SOURCE_DIR}/cmake")
  7.  
  8. find_package(Eigen 3.0 REQUIRED)
  9.  
  10. add_executable(camera_calib main.cpp )
  11.

总结

 

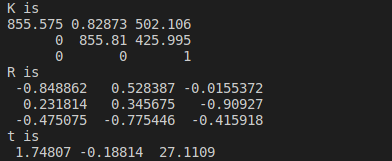
工程编译和运行：

编译：  
cd calibration_algorithm  
mkdir build  
cd build  
cmake ..  
make   

运行：

./camera_calib

运行的结果将在命令行中显示出来

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/盐析白兔/article/detail/127781
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号