羊村懒王

这个屌丝很懒，什么也没留下！

热门标签

2022美赛A题自行车到底怎么骑_22年美赛自行车

作者：羊村懒王 | 2024-02-28 21:07:47

踩

22年美赛自行车

今年美赛A题就是2021年东京奥运会奥地利女博士后Anna Kiesenhofer单枪匹马勇夺女子公路自行车比赛金牌故事的翻版，主题问题就是求解自行车运动员在近40km的赛程中应该如何分配功率以获得更好的成绩。

1.运动员功率模型

首先思考运动员的功率模型。运动员不可能长时间维持高功率输出，那么运动员的功率输出到底受什么限制呢？题目给出了一种“功率曲线”理论，这种理论指出运动员的功率（Power）与能维持该功率的最长时间（Duration）呈函数关系D=D(P)。

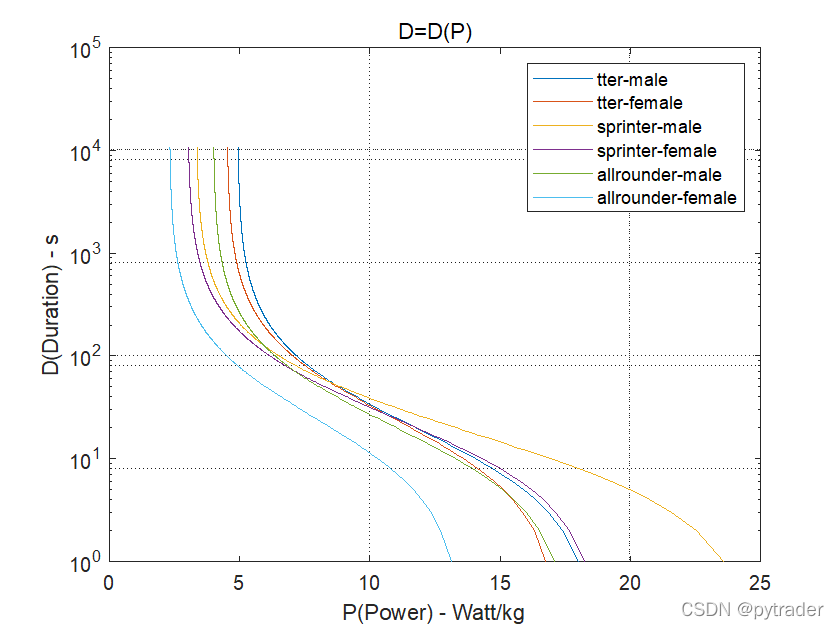
假设运动员以常功率P运行时间t，则约束方程

$t<D(P)$

那么问题是，如果运动员是以变功率P=P(t)运行呢？
当时我们为了简单起见，就将常功率P换成平均功率 $\bar{P}$ ，建立功率模型

$t<D(\bar{P})$

即

$t < D(\frac{1}{t}\int_{0}^{t}P(t')dt')$

这个公式就决定了运动过程中运动员功率输出P(t)满足的约束，不同选手的功率曲线不同，就决定了他们的冲刺能力、耐力。

2.动力学模型

有了运动员的功率P=P(t)，我们就可以求解自行车速度V=V(t)，进而求解比赛成绩T。
由功率P(t)得到速度V(t)的过程就是建立自行车动力学模型，最简单地，

$\left\{\begin{matrix} P(t)=\frac{\mathrm{d} }{\mathrm{d} t}E_{k}\\ \\ E_k=\frac{1}{2}MV^{2} \end{matrix}\right.$

功率完全作用给动能，即

$P(t)=\frac{\mathrm{d} }{\mathrm{d} t}(\frac{1}{2}MV^2)$

但实际上环境的阻力会分走很大一部分功率，首先考虑风阻

$f_{wind}=\alpha V^2$

以及滚阻

$f_{Rolling}=C_{rr}Mgcos\theta$

其中坡度

$\theta=sin^{-1}(\frac{\mathrm{d} H}{\mathrm{d} s})$

H为海拔，s为路程。
还要考虑重力势能

$E_p=MgH$

最终得到动力学方程

$\left\{\begin{matrix} P(t)=\frac{\mathrm{d} }{\mathrm{d} t}(\frac{1}{2}MV^2)+\alpha V^3+C_{rr}Mgcos(sin^{-1}(\frac{\mathrm{d} H}{\mathrm{d} s}))V+Mg\frac{\mathrm{d} H}{\mathrm{d} t}\\ \\ V=\frac{\mathrm{d} s}{\mathrm{d} t} \end{matrix}\right.$

3.赛道模型

题目要求对东京奥运会和比利时世锦赛两个赛道进行模型求解，就需要考虑赛道特征，其实主要就考虑两个特征：

（1）海拔

赛道海拔变化

$H=H(s)$

很简单。

（2）弯道

根据比赛地图算出各个点的曲率半径

$\rho =\rho (s)$

假设地面摩擦系数 $\mu$ ，需要运动员速度满足

$V<\sqrt{\mu g\rho}$

否则会被离心力甩出弯道，推导很简单，就不展开了。

最终，我们需要得到运动员在赛道不同位置的功率策略，即P=P(s)，所以还要把动力学方程中的P写成路程s的函数，得到完整的赛道模型：

$\left\{\begin{matrix} P(s)=\frac{\mathrm{d} }{\mathrm{d} t}(\frac{1}{2}MV^2)+\alpha V^3+C_{rr}Mgcos(sin^{-1}(\frac{\mathrm{d} H(s)}{\mathrm{d} s}))V+Mg\frac{\mathrm{d} H(s)}{\mathrm{d} t}\\ \\ t<D(\int_{0}^{t}P(s)dt'))\\ \\ V=\frac{\mathrm{d} s}{\mathrm{d} t} \\ \\ V<\sqrt{\mu g\rho(s)}\\ \\ S=\int_{0}^{T}Vdt \end{matrix}\right.$

4.模型求解

赛道模型求解就是求功率策略P=P(s)使得完赛时间T最短，即优化函数T=T{P(s)}的优化问题，由于赛道模型的方程组显然无法求解析解，我们不妨先将其离散化：

$\left\{\begin{matrix} P(s)\Delta t=\frac{1}{2}MV(t)^2+\alpha V(t)^3\Delta t+C_{rr}Mgcos(sin^{-1}(\frac{\mathrm{\Delta } H(s)}{\mathrm{\Delta } s}))V(t)\Delta t+Mg\Delta H(s)\\ \\ t<D(\sum_{0}^{t}P(s)\Delta t'))\\ \\ \Delta S=V(t)\Delta t\\ \\ V(t)<\sqrt{\mu g\rho(s)}\\ \\ S=\sum_{0}^{T}V(t)\Delta t \end{matrix}\right.$

只要有功率策略P(s)和初值V(0)=0，我们就可以递推地计算速度V(t)，最后得到T。
于是，我们可以在多项式时间内求得优化函数T{P(s)}，却无法在多项式时间内求出最优的P(s)，NP-hard理论限制我们只能用启发式的思维进行解的搜索，如模拟退火、蚁群算法、遗传算法等，当时我们用的是模拟退火。

模拟退火原理就不说了，主要就三步：

（1）产生初始解

初始解的产生很自由，我们当时是直接令功率曲线满载

$t=D(\int_{0}^{t}P(t')dt'))$

得到了一个解析式P(t)，将P(t)带入赛道方程得到时间-路程关系t=t(s)，再反向线性插值P(s)=P(t(s))作为初始解。

（2）产生随机解

利用当前解产生随机解的办法很多，我们当时是令

$P_{new}(s)=P(s)*A_{rand}*hanning(S_{rand},S_{rand}+L_{rand})$

$A_{rand}$ 是一个[-0.01,0.01]区间的随机幅度

$S_{rand}$ 是[0,S]区间的随机位置

$L_{rand}$ 是[0,L]区间的随机长度（L是个参数，决定了随机化的尺度）

hanning(x,y)是[x,y]区间的汉宁窗

（3）计算优化函数

假设一个虚拟骑手使用 $P_{new}(s)$ 作为功率策略参加比赛，用之前提到的方法，将 $P_{new}(s)$ 代入赛道模型就可以求出完赛时间T{ $P_{new}(s)$ }，比较 T{ $P_{new}(s)$ }和T{P(s)}以决定是否接受 $P_{new}(s)$ 作为一个新解，然后降低退火温度Tem，重复(2)(3)步骤。

退火过程中使用一个小技巧，就是令随机化尺度L随着退火温度Tem的降低而降低，即L=L(Tem)，这样虚拟骑手就会先尝试大范围的策略调整，再逐渐缩小调整范围，最终适应赛道，可以节省不少程序运行时间。

5.求解结果

（1）东奥会赛道

用灰色曲线表示赛道海拔，红色曲线表示功率策略，首先虚拟骑手以初始解为策略完成比赛，用时4139秒。

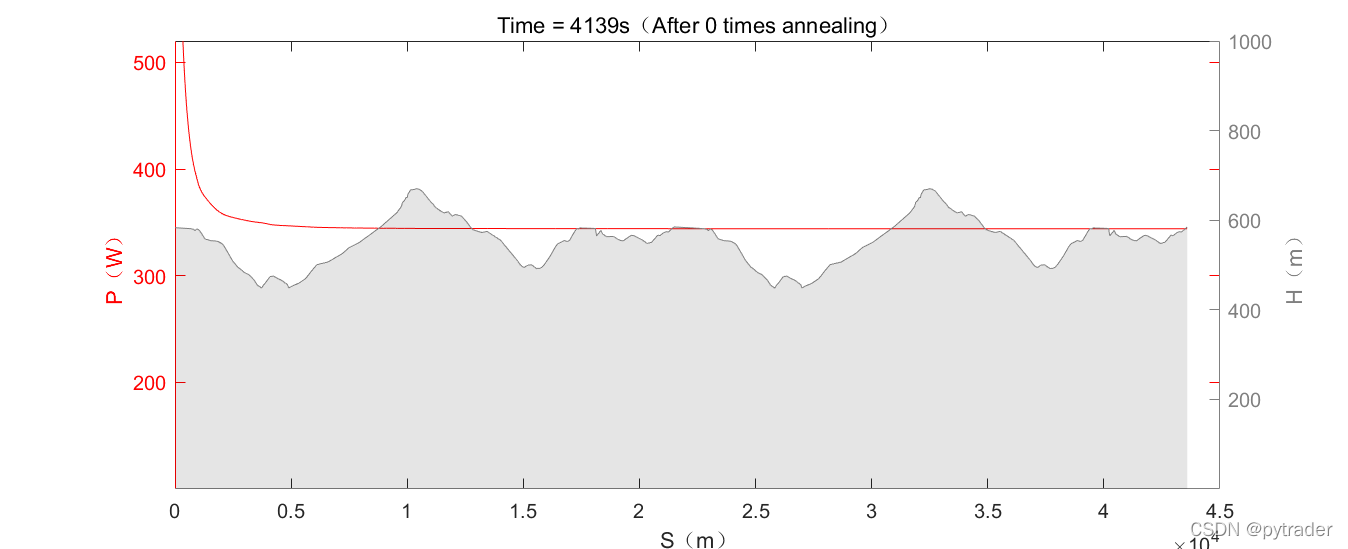
经过5000次模拟退火后，虚拟骑手完赛时间降到了4102秒。可以观察到在这个过程中，骑手尝试从整体上调整功率策略，在上坡时增加功率，下坡时降低功率，最后成功节省完赛时间。

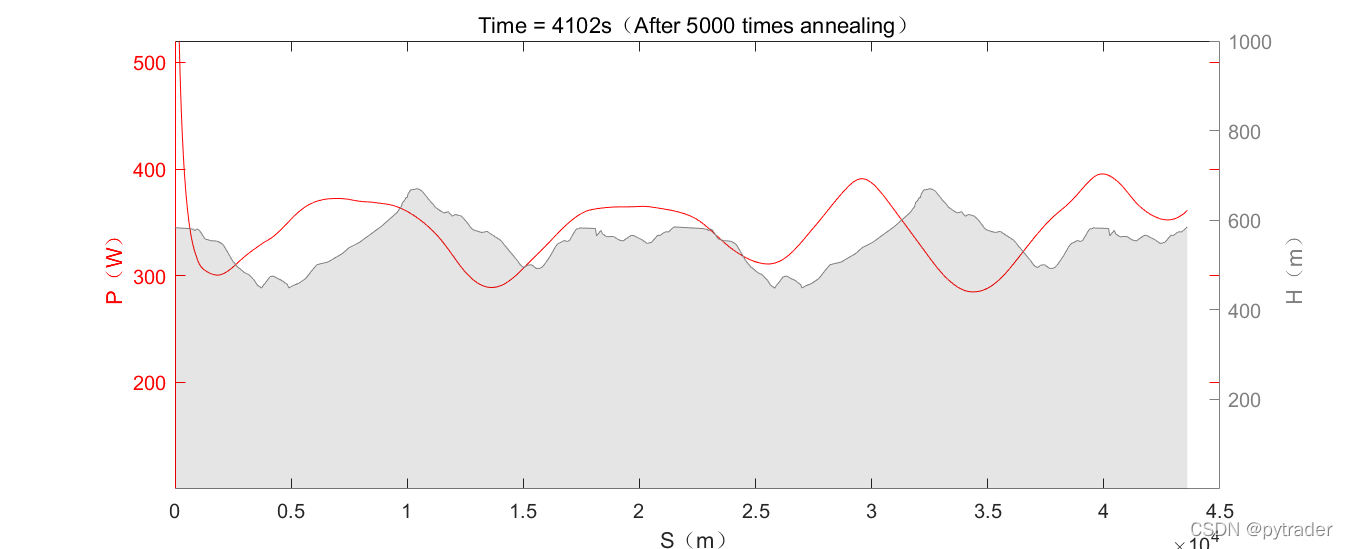
在接下来的20000次退火中，随着退火温度降低，随机化尺度L也跟着下降，意味着虚拟骑手会尝试在更小的尺度上优化功率策略，以适应崎岖不平的地形，最后将完赛时间降到了4046秒。

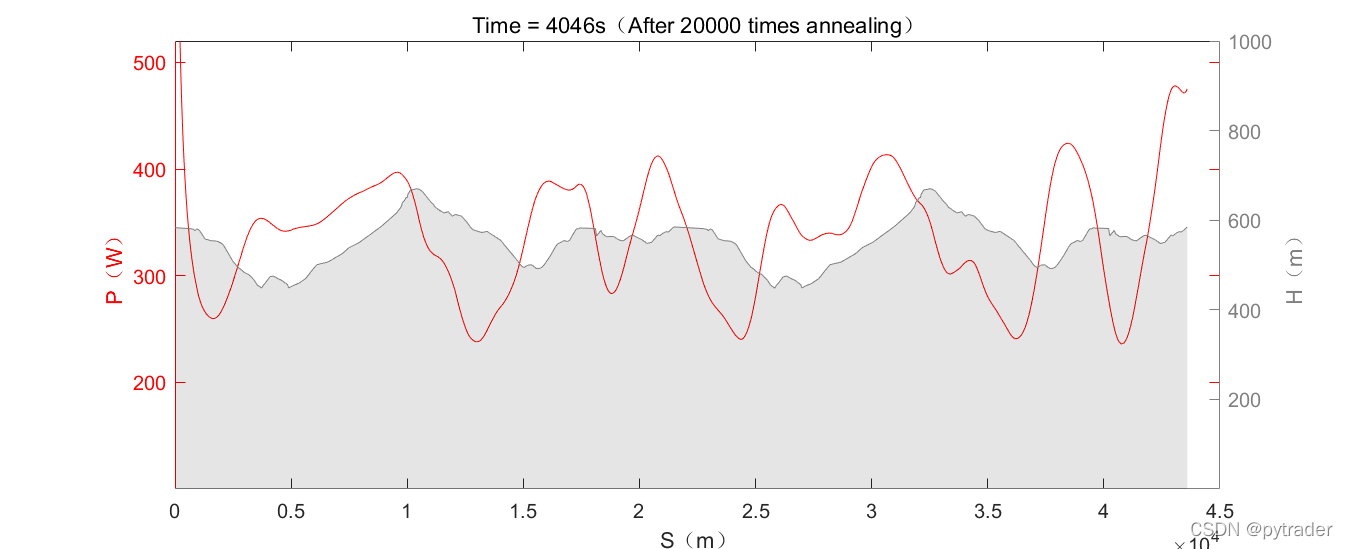
在40000次退火之后，虚拟骑手的功率策略已经达到了非常细致的程度，完赛时间也降到了4023秒。

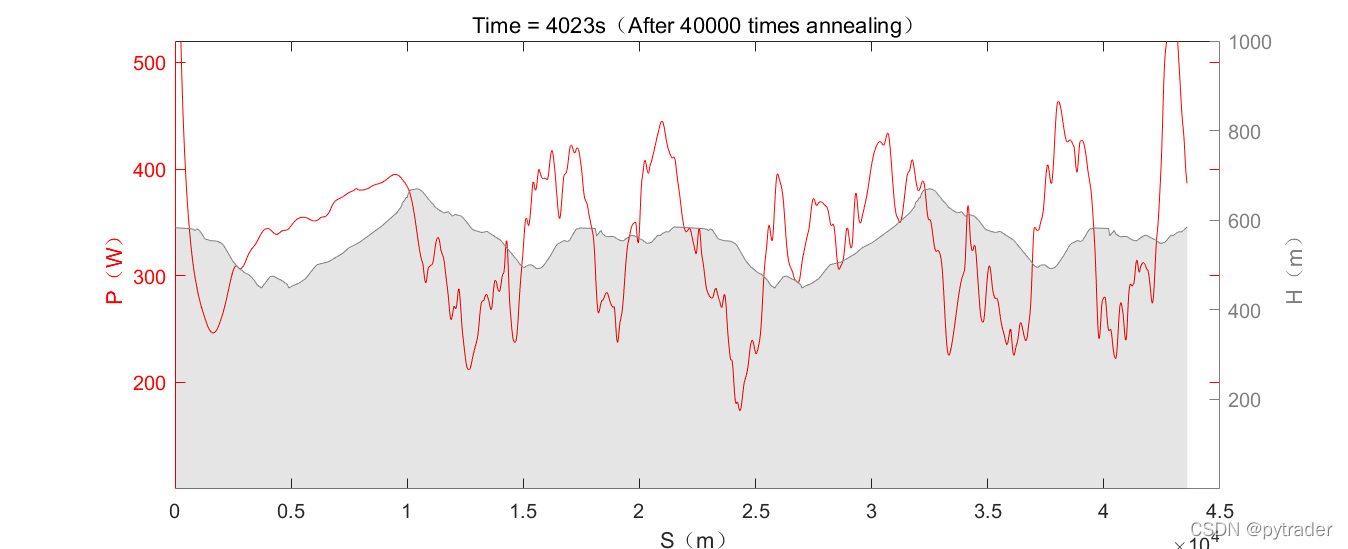
完赛时间随退火次数增加而缩短：

我们再观察退火过程中速度曲线的变化：

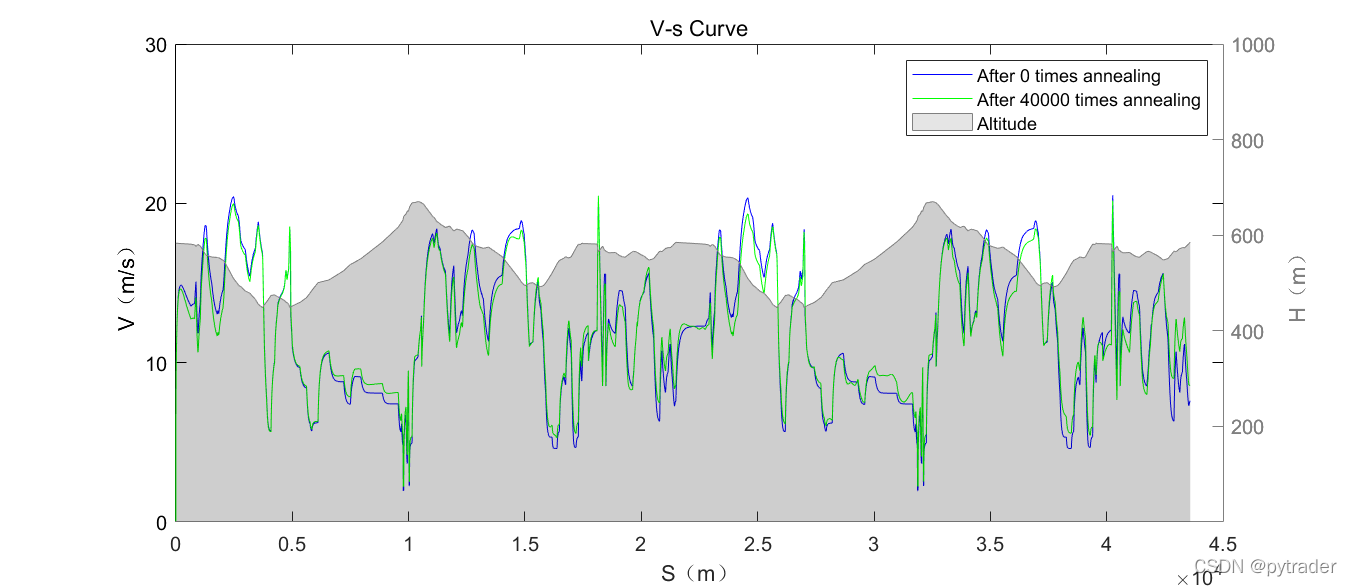
似乎经过退火，速度曲线变得平稳了。我们对速度曲线做一个方差分析：

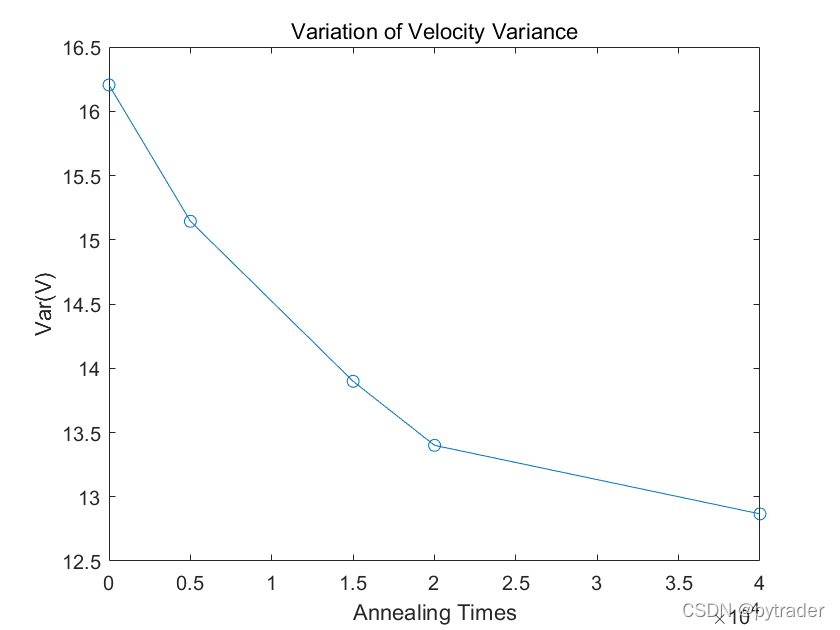
可以发现速度的方差确实随着功率策略的优化而降低，所以骑手在比赛过程中应该尽量保持速度平稳。而且Var(V)和T随退火次数的变化趋势几乎相同，说明在功率曲线的约束下ΔT和Var(V)是有某种确定的正相关关系的，当时我们认为可以通过泛函分析的方法进行研究，可惜时间不允许，故作罢。
那么虚拟骑手是如果保持速度平稳的呢？通过观察P-s曲线可以发现，主要策略是根据地面坡度调整功率输出，为了验证这一点，我们画40000次退火后功率P在坡度 $\theta$ 空间的分布：

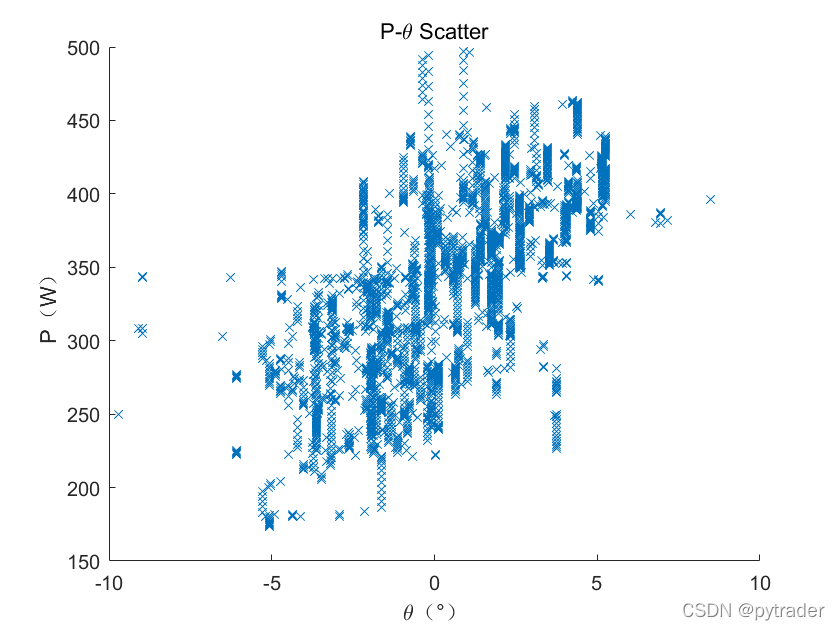
可以看出功率策略在地面坡度空间有明显的趋势，我们做一个线性回归：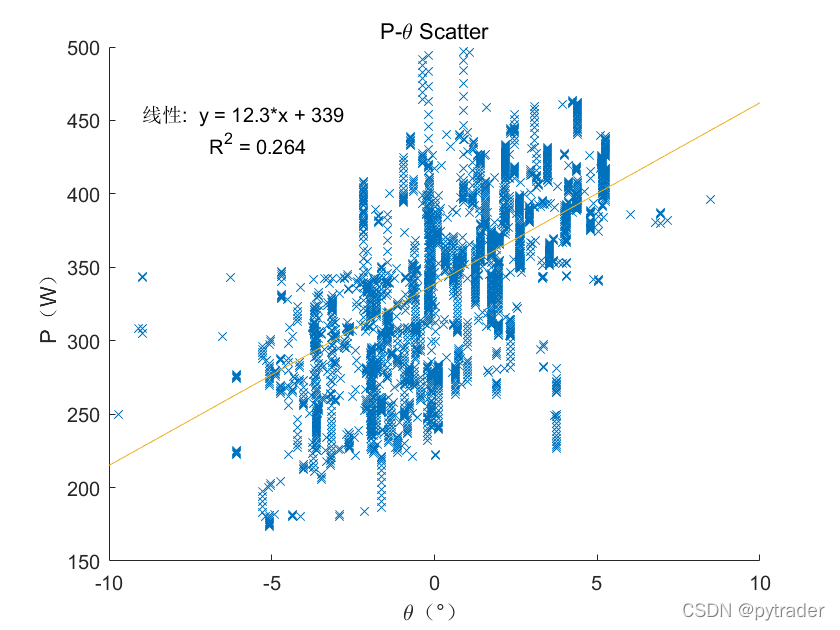

拟合式给出

$P=12.3*\theta(^{\circ})+339\ (W)$

这说明骑手在平地上应该以339W输出功率，而坡度每增加1°就应该增加3.6%的功率。

（2）世锦赛赛道

2021年比利时世锦赛的赛道几乎没有海拔变化，全程平地，使得前40000次退火几乎没有成效，完赛时间不减反增，说明在平地上对功率策略的整体调整作用不大，功率曲线满载已经是不错的策略。

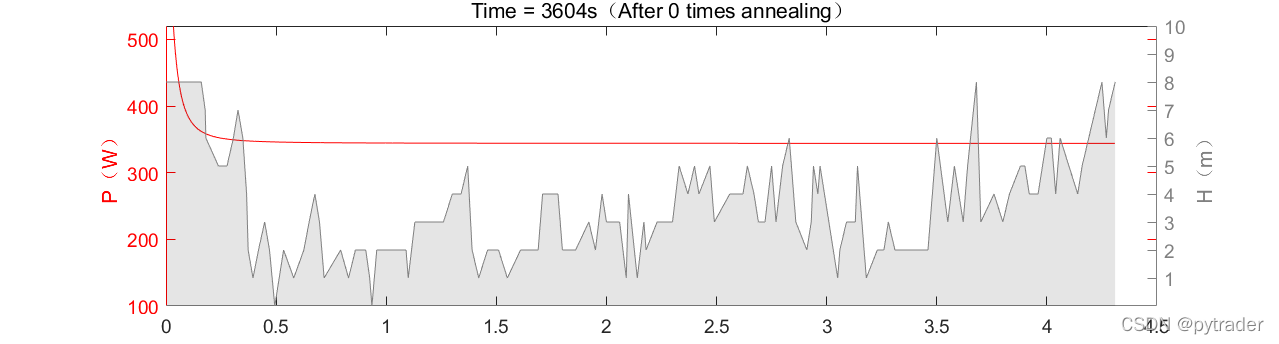
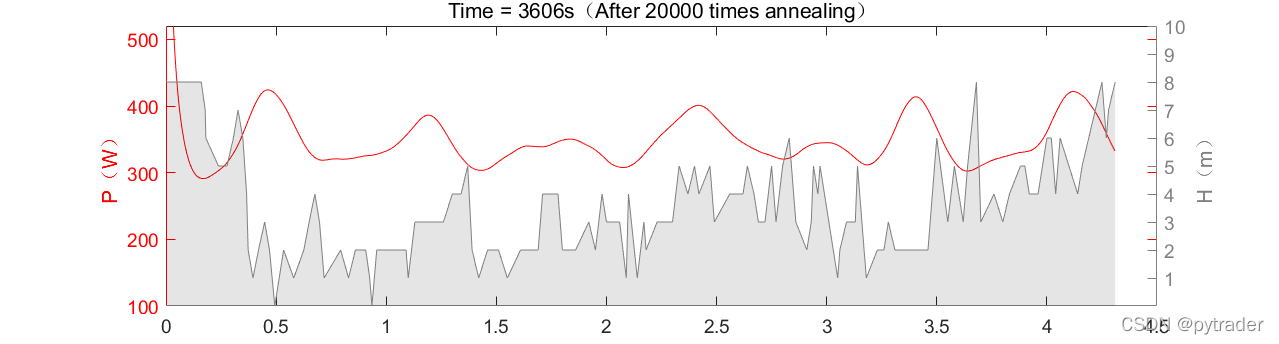
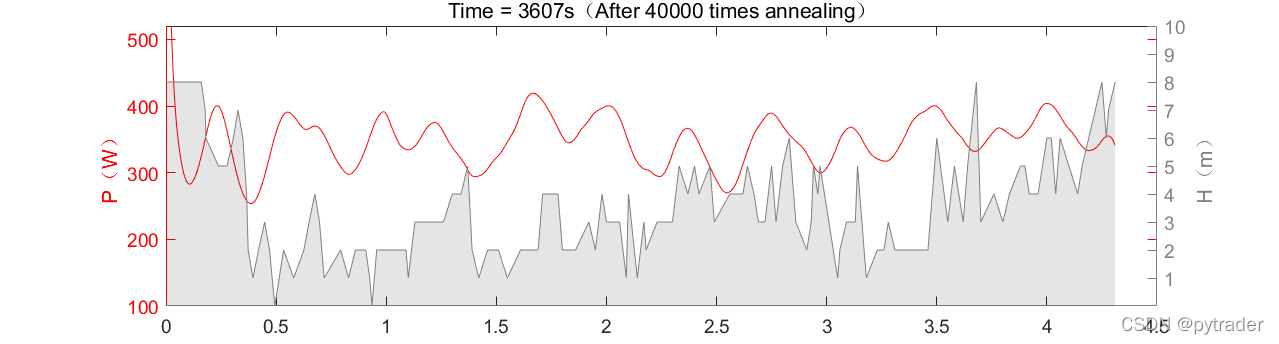
而当退火次数达到100000次以上时优化效果开始显现：

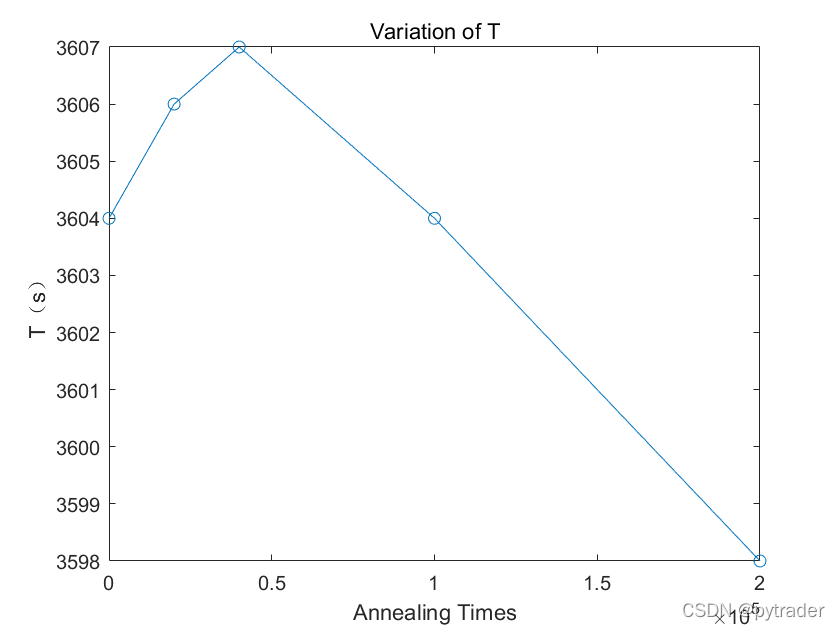
虽然节省的时间不多，但是完赛时间呈现明显的下降趋势，随着进一步退火还可以更优化，但当时出于时间紧迫就没有跑更多点（200000次退火需要Matlab运行约3小时）。
为了研究虚拟骑手到底是在什么地方进行了优化，我们画0次退火和200000次退火的速度曲线：

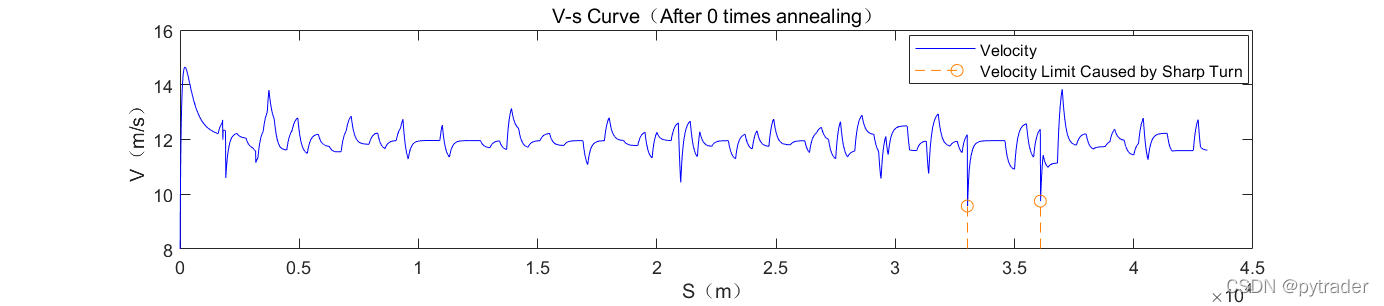
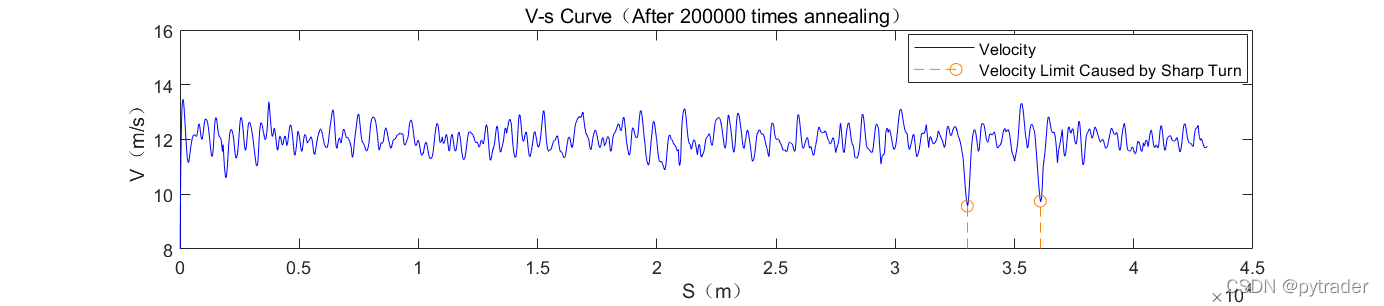
其中橙色虚线表示急转弯带来的速度限制，骑手在该位置必须减速到指定数值才能避免被离心力甩出赛道。
放大两处急转弯处的图像：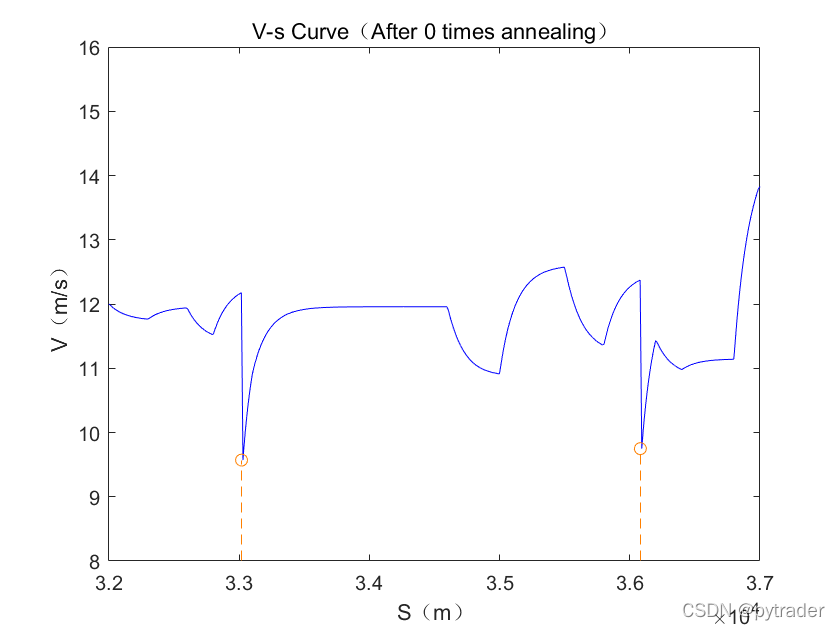

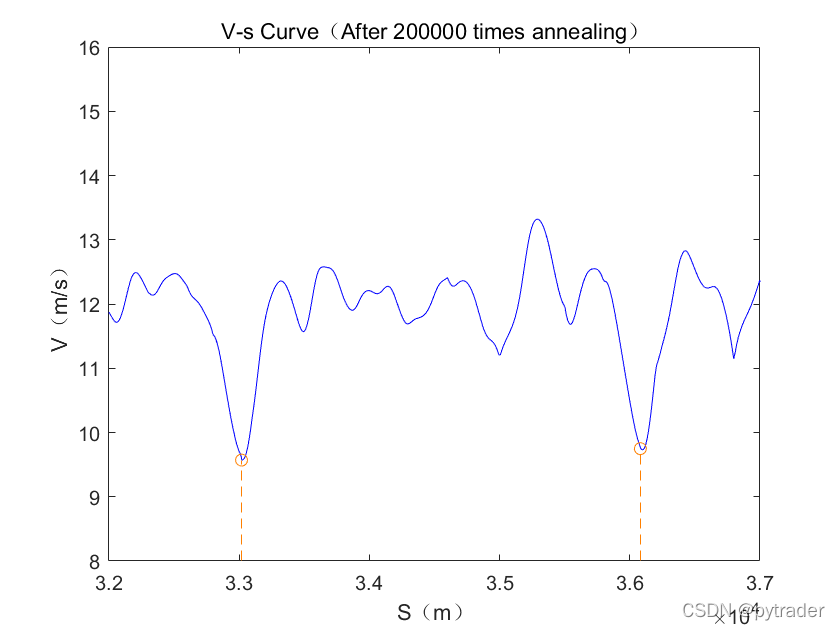
可以观察到，优化前，骑手会正常速度行驶到弯道处，通过急刹车降低速度，以满足弯道限制；而优化后，骑手会提前减速节省体力，到弯道处刚好能够过弯，过弯后利用节省的体力大力加速，快速恢复速度。
为了验证这一点，我们画弯道附近的功率策略：

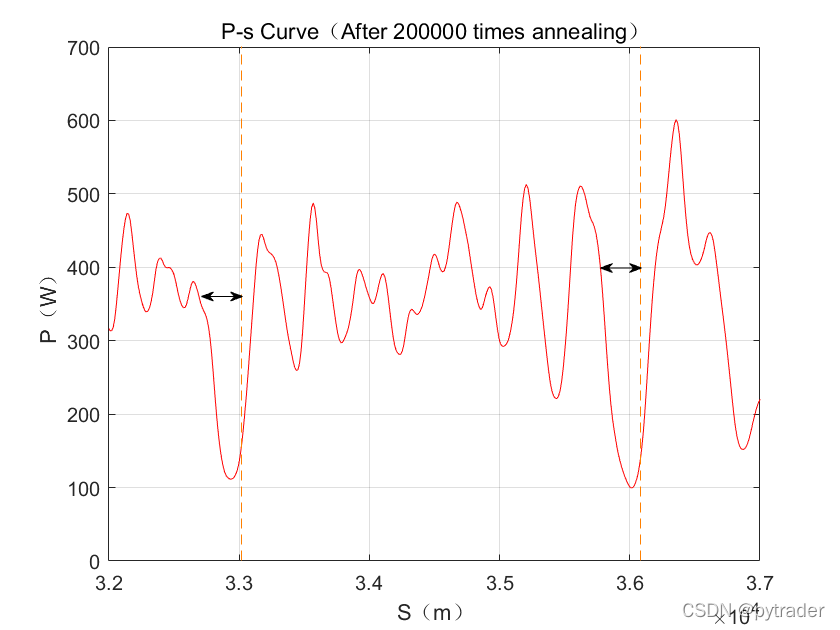
可以观察到虚拟骑手过弯时会提前300米左右开始减速，慢慢将功率降到30%以下，到达弯道时速度刚好能过弯，并且不用捏刹车。
所以，对于UCI这种较为平坦的赛道来说，主要的优化对象是过弯时的策略，虽然对结果的影响程度没有地势那么大，但还是自行车运动员在比赛过程中需要考虑的因素。

题目还要求自己设计一个赛道并求解，现在想来可以在里面设计不同曲率的弯道，来研究预减速距离、减速功率与弯道曲率的关系，但当时没考虑那么多，就随便设计了一个赛道，结论跟上面差不多。

6.结论

（1）功率输出总体上要使功率曲线满载

（2）上坡提升功率，下坡降低功率，坡度每高1°提升3.6%

（3）过弯前300m开始减速，慢慢将功率降到30%以下，过弯时速度刚好满足离心力限制

（4）保持速度平稳

还有其他各种细节省略ing...

最后是美赛本身的一点总结(ᐛ)
我们队三人都是第一次参加数学建模比赛，最后能够顺利解决问题，算得上是一次成功的参赛经历乐(๑¯◡¯๑)虽然赛后感觉经验这个东西还是很重要，尤其是时间规划上...论文一定要提前提前提前开始写！！！
不过最后总算是踩着点交上了(′▽`)比赛前也恶补了很多课外知识（指你系核心课什么也没有讲x），最后感谢两位超可爱超厉害队友啊啊啊o((>ω< ))o

声明：本文内容由网友自发贡献，转载请注明出处：【wpsshop】