万字长文系统讲解模型特征选择方法，这一篇就够了！

上个月扫读完《阿里云天池大赛赛题解析》[1]后，看到书中对特征选择的讲述，于是便打算借此机会，系统梳理下各种特征选择方法。

今天正好有时间进行梳理，内容较长建议慢慢品读，欢迎收藏、喜欢点赞支持。文末有交流群，欢迎加入讨论

一、背景介绍

在处理结构型数据时，特征工程中的特征选择是很重要的一个环节，特征选择是选择对模型重要的特征。它的好处[2]在于:

● 减少训练数据大小，加快模型训练速度。

● 减少模型复杂度，避免过拟合。

● 特征数少，有利于解释模型。

● 如果选择对的特征子集，模型准确率可能会提升。

我曾在文章CCF大赛项目: 大数据时代Serverless工作负载预测，提到过一个困境，就是当时我在滑动窗口式组织数据 + 多阶统计特征生成后，我的模型就过拟合了，然后我看到某选手开源的代码，他只用了LGBM模型认为重要的TOP几百个特征就能达到跟我用全量特征的效果。所以我就反思到：特征真的越多越好吗？把特征交给模型，模型自己能很好学习到哪些特征有用或者没用吗？当时，我抱着疑问，做了特征选择工作，发现效果居然有提升，可能原因是：

● 去除冗余无用特征，减低模型学习难度，减少数据噪声。

● 去除标注性强的特征，例如某些特征在训练集和测试集分布严重不一致，去除他们有利于避免过拟合。

● 选用不同特征子集去预测不同的目标，比如用不同状态下的作业数特征去预测"提交中的作业数"，而用不同资源使用率的特征去预测“CPU使用率”。

当时，我是直接一股脑把特征丢进去训练模型，后面比赛完跟其它选手交流才了解到特征选择的重要性。所以这篇文章的出发点是自我查漏补缺，也希望能给大家带来点帮助。

特征选择方法一共分为3类：过滤法(Filter)、包裹法(Wrapper)和嵌入法(Embedded)。下面我会依次介绍它们。

二、过滤法(Filter)

图1: 过滤法[3]

过滤法: 选择特征时不管模型，该方法基于特征的通用表现去选择，比如: 目标相关性、自相关性和发散性等。

● 优点: 特征选择计算开销小，且能有效避免过拟合。

● 缺点: 没考虑针对后续要使用的学习器去选择特征子集，减弱学习器拟合能力。

当我们使用过滤法去审视变量时，我们会从单变量自身情况和多变量之间的关系去判断变量是否该被过滤掉。

图2: 过滤法方法总结

1. 单变量

(1) 缺失百分比(Missing Percentage)

缺失样本比例过多且难以填补的特征，建议剔除该变量。

(2) 方差(Variance)

若某连续型变量的方差接近于0，说明其特征值趋向于单一值的状态，对模型帮助不大，建议剔除该变量。

(3) 频数(Frequency)

若某类别型变量的枚举值样本量占比分布，集中在单一某枚举值上，建议剔除该变量。

这里以波士顿房价数据集举例，样例代码如下:

# load Boston dataset
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data, columns = boston.feature_names)

# Missing Percentage + Variance
stat_df = pd.DataFrame({'# of miss':df.isnull().sum(),
                        '% of miss':df.isnull().sum() / len(df) * 100,
                        'var':df.var()})

# Frequency
cat_name = 'CHAS'
chas = df[cat_name].value_counts().sort_index()
cat_df = pd.DataFrame({'enumerate_val':list(chas.index), 'frequency':list(chas.values)})
sns.barplot(x = "enumerate_val", y = "frequency",data = cat_df, palette="Set3")
for x, y in zip(range(len(cat_df)), cat_df.frequency):
    plt.text(x, y, '%d'%y, ha='center', va='bottom', color='grey')
plt.title(cat_name)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

图3: 单变量分析(缺失值、方差和频次图)

由图3发现，NOX方差低和CHAS频次分布严重不平衡，可以考虑剔除。

2. 多变量

研究多变量之间的关系时，主要从两种关系出发:

● 自变量与自变量之间的相关性: 相关性越高，会引发多重共线性问题，进而导致模型稳定性变差，样本微小扰动都会带来大的参数变化[5]，建议在具有共线性的特征中选择一个即可，其余剔除。

● 自变量和因变量之间的相关性: 相关性越高，说明特征对模型预测目标更重要，建议保留。

由于变量分连续型变量和类别型变量，所以在研究变量间关系时，也要选用不同的方法:

2.1 连续型vs连续型

(1) 皮尔逊相关系数(Pearson Correlation Coefficient)

Pearson相关系数是两个变量的协方差除以两变量的标准差乘积。协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），而除以标准差后，Pearson的值范围为[-1,1]。当两个变量的线性关系增强时，相关系数趋于1或-1，正负号指向正负相关关系。[6]

(2) 斯皮尔曼相关系数(Spearman’s Rank Correlation Coefficient)

Pearson相关系数是建立在变量符合正态分布的基础上，而Spearman相关系数不假设变量服从何种分布，它是基于**等级(rank)**的概念去计算变量间的相关性。如果变量是顺序变量(Ordinal Feature)，推荐使用Spearman相关系数。

其中， 为两个变量的等级差值， 为等级个数。这里举个例子会更好理解，假设我们要探究连续型变量 和 的Spearman相关系数，计算过程如下：

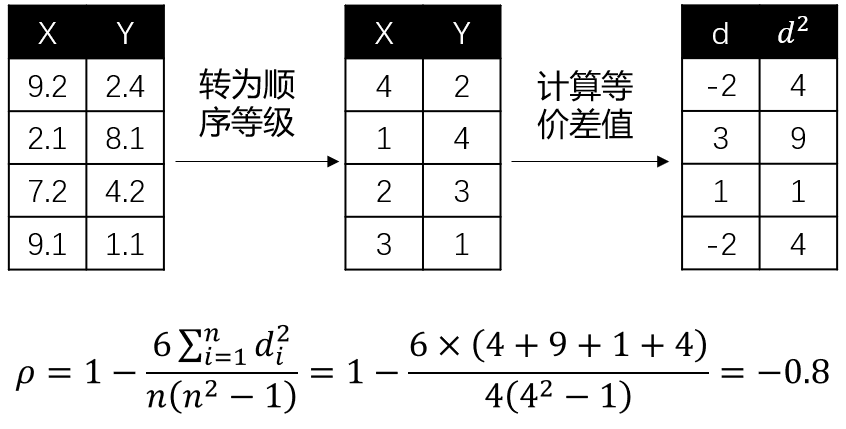
图4: Spearman相关系数

同样地，相关系数趋于1或-1，正负号指向正负相关关系。

2.2 连续型vs类别型

(1) 方差分析(Analysis of variance, ANOVA)

ANOVA的目的是检验不同组下的平均数是否存在显著差异。举个例子，我们要判断1,2和3班的同学的数学平均分是否有显著区别？我们能得到，班级为类别型变量，数学分数为连续型变量，如果班级与数学分数有相关性，比如1班同学数学会更好些，则说明不同班的数学平均分有显著区别。为了验证班级与数学分数的相关性，ANOVA会先建立零假设： : (三个班的数学分数没有显著区别)，它的验证方式是看组间方差(Mean Squared Between, MSB)是否大于组内方差(Mean Squared Error, MSE)，如果组间方差>组内方差，说明存在至少一个分布相对于其他分布较远，则可以考虑拒绝零假设。[7]

基于纽约Johnny哥在知乎“什么是ANOVA”的回答[8]，我们举例来试着计算下：

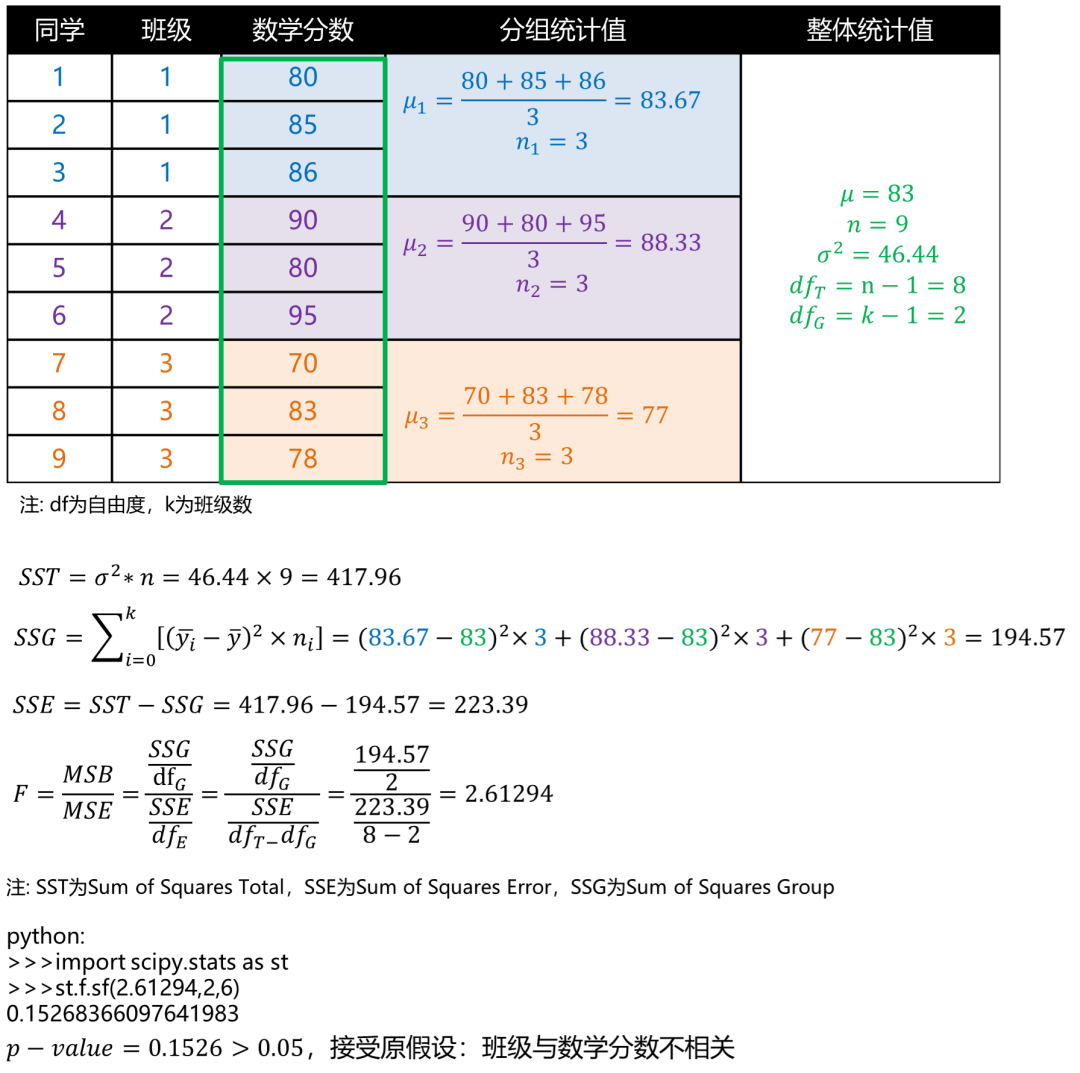
图6: ANOVA分析案例

注意，ANOVA分析前需要满足3个假设: 每组样本具备方差同质性、组内样本服从正态分布，样本间需要独立。[7]

(2) 肯德尔等级相关系数(Kendall tau rank correlation coefficient)

假设我们要评价学历与工资的相关性，Kendall系数会对按学历对样本排序，若排序后，学历和工资排名相同，则Kendall系数为1，两变量正相关。若学历和工资完全相反，则系数为-1，完全负相关。而如果学历和工资完全独立，系数为0。Kendall系数计算公式如下：

其中， 为同序对， 为异序对， 为总对数。同样地，我们举例展示下计算过程：

图7: Kendall相关系数

2.3 类别型vs类别型

(1) 卡方检验(Chi-squared Test)

卡方检验可用于检验两个类别型变量之间的相关性。它建立的零假设是：两变量之间不相关。卡方值 的计算公式如下：

其中， 是实际值， 是理论值。卡方值的目的是衡量理论和实际的差异程度。如果我们研究运动的人是否会受伤，计算过程如下：

图8: 卡方检验

卡方值高，说明两变量之间具有相关性的可能性更大。

(2) 互信息(Mutual Information)

互信息是衡量变量之间相互依赖程度，它的计算公式如下：

它可以转为熵的表现形式，其中 和 是条件熵， 是联合熵。当 与 独立时， ，则互信息为0。当两个变量完全相同时，互信息最大，因此互信息越大，变量相关性越强。此外，互信息是正数且具有对称性(即 )。

图9: 互信息[9]

3. 过滤法总结

总结以上内容，如下图所示:

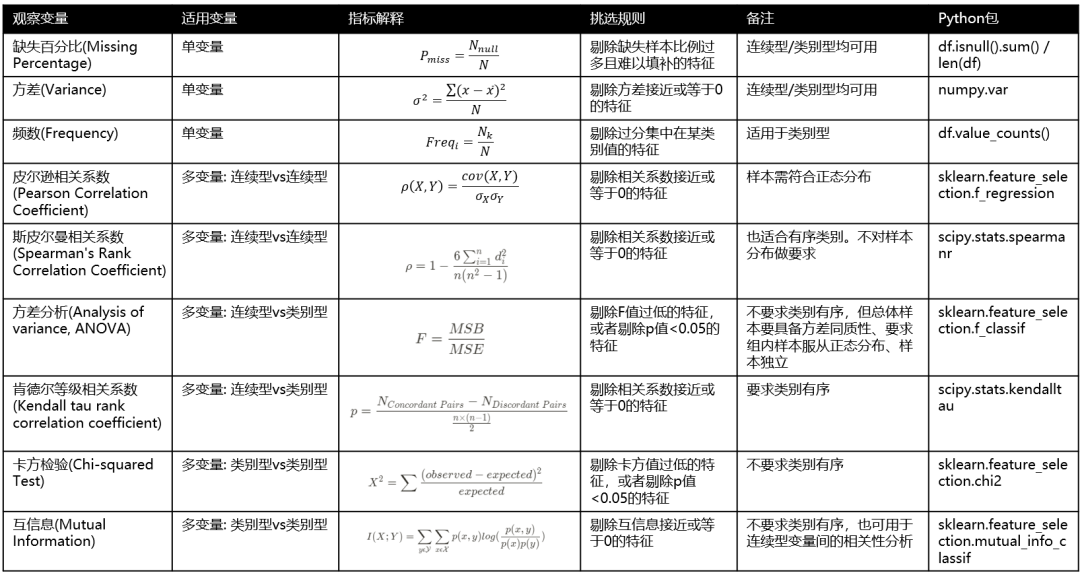
图10: 过滤法的度量指标汇总（注：挑选规则是基于自变量和因变量的相关性去挑选）

我们可以按需使用上面的指标去观察变量间的相关性，然后人工挑选特征。另外，也能使用scikit-learn里的特征选择库sklearn.feature_selection[10]，这里我以SelectKBest(选择Top K个最高得分的特征)为例:

# load Boston dataset
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression

boston = load_boston()
df = pd.DataFrame(boston.data, columns = boston.feature_names)
target = pd.DataFrame(boston.target, columns=['MEDV'])
print('X.shape:', df.shape)

# select feature by person coefficient
X = np.array(df)
Y = np.array(target)
skb = SelectKBest(score_func=f_regression, k=5)
skb.fit(X, Y.ravel())
print('选择的特征有:', [boston.feature_names[i] for i in skb.get_support(indices = True)])
X_selected = skb.transform(X)
print('X_selected.shape:', X_selected.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

三、包裹法(Wrapper)

图11: 包裹法[3]

包裹法: 将要使用的学习器的性能作为特征子集的评价准则，目的是为给的学习器选择“量身定做”的特征子集。[4]

● 优点: 特征选择比过滤法更具针对性，对模型性能有好处。

● 缺点: 计算开销更大。

包裹法有如下三类搜索方法:

图12: 包裹法总结

1. 完全搜索

遍历所有可能组合的特征子集，然后输入模型，选择最佳模型分数的特征子集。不推荐使用，计算开销过大。

2. 启发式搜索

启发式搜索是利用启发式信息不断缩小搜索空间的方法。在特征选择中，模型分数或特征权重可作为启发式信息。

2.1 向前/向后搜索

向前搜索是先从空集开始，每轮只加入一个特征，然后训练模型，若模型评估分数提高，则保留该轮加入的特征，否则丢弃。反之，向后特征是做减法，先从全特征集开始，每轮减去一个特征，若模型表现减低，则保留特征，否则弃之。

2.2 递归特征消除

递归特征消除简称RFE(Recursive Feature Elimination)，RFE是使用一个基模型进行多轮训练，每轮训练后，消除若干低权值(例特征权重系数或者特征重要性)的特征，再基于新的特征集进行下一轮训练[1]。RFE使用时，要提前限定最后选择的特征数(n_features_to_select)，这个超参很难保证一次就设置合理，因为设高了，容易特征冗余，设低了，可能会过滤掉相对重要的特征。而且RFE只是单纯基于特征权重去选择，没有考虑模型表现，因此RFECV出现了，REFCV是REF + CV(交叉验证)，它的运行机制是：先使用REF获取各个特征的ranking，然后再基于ranking，依次选择[min_features_to_select, len(feature)]个特征数量的特征子集进行模型训练和交叉验证，最后选择平均分最高的特征子集。

图13: RFE 与RFECV

这里不重复造轮子了，可参考wanglei5205提供样例代码[10]:

### 生成数据
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000,         # 样本个数
                           n_features=25,          # 特征个数
                           n_informative=3,        # 有效特征个数
                           n_redundant=2,          # 冗余特征个数（有效特征的随机组合）
                           n_repeated=0,           # 重复特征个数（有效特征和冗余特征的随机组合）
                           n_classes=8,            # 样本类别
                           n_clusters_per_class=1, # 簇的个数
                           random_state=0)

### 特征选择
# RFE
from sklearn.svm import SVC
svc = SVC(kernel="linear")

from sklearn.feature_selection import RFE
rfe = RFE(estimator = svc,           # 基分类器
          n_features_to_select = 2,  # 选择特征个数
          step = 1,                  # 每次迭代移除的特征个数 
          verbose = 0                # 显示中间过程
          ).fit(X,y)
X_RFE = rfe.transform(X)
print("RFE特征选择结果——————————————————————————————————————————————————")
print("有效特征个数 : %d" % rfe.n_features_)
print("全部特征等级 : %s" % list(rfe.ranking_))

# RFECV
from sklearn.svm import SVC
svc = SVC(kernel="linear")

from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import RFECV
rfecv = RFECV(estimator=svc,          # 学习器
              min_features_to_select=2, # 最小选择的特征数量
              step=1,                 # 移除特征个数
              cv=StratifiedKFold(2),  # 交叉验证次数
              scoring='accuracy',     # 学习器的评价标准
              verbose = 0,
              n_jobs = 1
              ).fit(X, y)
X_RFECV = rfecv.transform(X)
print("RFECV特征选择结果——————————————————————————————————————————————————")
print("有效特征个数 : %d" % rfecv.n_features_)
print("全部特征等级 : %s" % list(rfecv.ranking_))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

3. 随机搜索

3.1 随机特征子集

随机选择多个特征子集，然后分别评估模型表现，选择评估分数高的特征子集。

3.2 Null Importance

3年前Kaggle GM Olivier提出Null Importance特征挑选法，最近看完代码，觉得真妙。它成功找出“见风使舵”的特征并剔除了它们，什么是“见风使舵”的特征呢？多见于标识性强或充满噪声的特征，举个例子，如果我们把userID作为特征加入模型，预测不同userID属于哪类消费人群，一个过拟合的模型，可以会学到userID到消费人群的直接映射关系(相当于模型直接记住了这个userID是什么消费人群)，那如果我假装把标签打乱，搞个假标签去重新训练预测，我们会发现模型会把userID又直接映射到打乱的标签上，最后真假标签下，userID“见风使舵”地让都自己变成了最重要的特征。我们怎么找出这类特征呢？Olivier的想法很简单：真正强健、稳定且重要的特征一定是在真标签下特征很重要，但一旦标签打乱，这些优质特征的重要性就会变差。相反地，如果某特征在原始标签下表现一般，但打乱标签后，居然重要性上升，明显就不靠谱，这类“见风使舵”的特征就得剔除掉。

Null Importance的计算过程大致如下:

(1) 在原始数据集运行模型获取特征重要性;

(2) shuffle多次标签，每次shuffle后获取假标签下的特征重要性;

(3) 计算真假标签下的特征重要性差异，并基于差异，筛选特征。

图14: Null Importance的计算过程示意图

在图14我们能知道Null Importance的大致运行流程，但这里补充些细节，其中，重要性你可以选择importance_gain或者importance_split。另外，如图14所示，如果我们要比较原始标签和打乱标签下的特征重要性，Olivier提供了两种比较方法：

第一种：分位数比较。

和1是为了避免 和分母为0的情况。输出样例如下：

图15: 比较特征重要性分位数

第二种：次数占比比较。

正常来说，单个特征只有1个 ，之所以作者要求25分位数，是考虑到如果使用时，我们也对原始特征反复训练生成多组特征重要性，所以才就加了25分位数。输出样例如下：

图16: 比较特征重要性次数占比

由上可知，第二种方法得到的特征分数是在0-100范围内，因此Olivier选择在第二种方法上，采用不同阈值去筛选特征，然后评估模型表现。推荐阅读Olivier的开源代码[11]，简单易懂。

4. 包裹法总结

实际使用中，推荐RFECV和Null Importance，因为他们既考虑了特征权重也考虑了模型表现。

四、嵌入法(Embedded)

图17: 嵌入法[3]

嵌入法: 特征选择被嵌入进学习器训练过程中。不像包裹法，特性选择与学习器训练过程有明显的区分。[4]

● 优点: 比包裹法更省时省力，把特征选择交给模型去学习。

● 缺点: 增加模型训练负担。

常见的嵌入法有LASSO的L1正则惩罚项、随机森林构建子树时会选择特征子集。嵌入法的应用比较单调，sklearn有提供SelectFromModel[12]，可以直接调用模型挑选特征。参考样例代码[1]如下:

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import GradientBoostingClassifier

iris = load_iris()

# 将待L1惩罚项的逻辑回归作为基模型的特征选择
selected_data_lr = SelectFromModel(LogisticRegression(penalty='l1', C = 0.1, solver = 'liblinear'), max_features = 3).fit_transform(iris.data, iris.target)

# 将GBDT作为基模型的特征选择
selected_data_gbdt = SelectFromModel(GradientBoostingClassifier(), max_features = 3).fit_transform(iris.data, iris.target)

print(iris.data.shape)
print(selected_data_lr.shape)
print(selected_data_gbdt.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

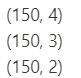
五、总结

在进行特征选择时，建议过滤法、包裹法和嵌入法都尝试使用，前期的特征过滤有利于减轻模型的学习负担。当然最高级的特征选择还是基于业务知识的人工挑选，以上方法挑选出的特征也建议多思考为什么这个特征对模型有帮助，以及挑选的优质特征有没有更进一步深入挖掘的可能。

参考资料

[1] 《阿里云天池大赛赛题解析—机器学习篇》- 天池平台

[2] Introduction to Feature Selection methods with an example (or how to select the right variables? - Saurav Kaushik, 文章链接: https://www.analyticsvidhya.com/blog/2016/12/introduction-to-feature-selection-methods-with-an-example-or-how-to-select-the-right-variables/#:~:text=The main differences between the,training a model on it

[3] Feature selection - wikipedia, 百科链接: https://en.wikipedia.org/wiki/Feature_selection#Main_principles

[4] 《机器学习》- 周志华

[5] 关于多重共线性 - my breath, 文章链接: https://zhuanlan.zhihu.com/p/96793075

[6] 如何理解皮尔逊相关系数（Pearson Correlation Coefficient）？- 知乎，回答链接: https://www.zhihu.com/question/19734616

[7] 对方差分析（ANOVA）的直观解释及计算 - 知乎，回答链接: https://zhuanlan.zhihu.com/p/57896471

[8] 什么是ANOVA? - 知乎，回答链接: https://www.zhihu.com/question/320487814

[9] 互信息 - 搜狗百科, 百科链接: https://baike.sogou.com/v363043.htm?fromTitle=互信息

[10] 【特征选择】包裹式特征选择法 - wanglei5205, 博客链接: https://www.cnblogs.com/wanglei5205/p/8977467.html

[11] Feature Selection with Null Importances - Olivier, Kaggle链接: https://www.kaggle.com/ogrellier/feature-selection-with-null-importances/notebook

[12] sklearn.feature_selection.SelectFromModel - scikit-learn, 文档链接: https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.SelectFromModel.html

转自：https://mp.weixin.qq.com/s/7U8YM7bYYSfdtlLbrMVu0w

---

技术交流

欢迎转载、收藏、有所收获点赞支持一下！

目前开通了技术交流群，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友

• 方式①、发送如下图片至微信，长按识别，后台回复：加群；
• 方式②、添加微信号：dkl88191，备注：来自CSDN
• 方式③、微信搜索公众号：Python学习与数据挖掘，后台回复：加群