常见数量关系分析_买3张票,每张买到的概率都是80%,最后买到票的概率是多少

考点一

相遇追及问题

（一）直线型

1. 单次相遇：相距两地，同时出发，相向而行。

2. 单次追及：同时出发，同向而行。

3. 直线型相遇追及问题公式总结

（二）环线型

环线型相遇追及问题公式总结

式中“S”为环的周长。

实例1

甲、乙两车分别以30公里/小时和40公里/小时的速度同时匀速从A地开往B地，丙车以50公里/小时的速度匀速从B地开往A地。A、B两地距离120公里。问丙车遇到乙车后多久会遇到甲车?（ ）

A. 8分钟 B. 10分钟 C. 12分钟 D. 15分钟

解析

根据题意，题目中有两个相遇的过程，分别是丙与甲相遇和丙与乙相遇，假设丙与甲相遇的时间为t1，与乙相遇的时间为t2，由相遇的公式可列：

120=(30+50)t1，120=(40+50)t2，解得

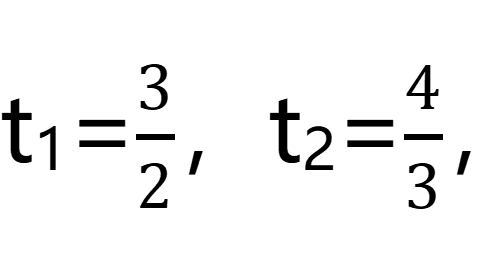
，题目所求为两个相遇过程之间的时间差，即

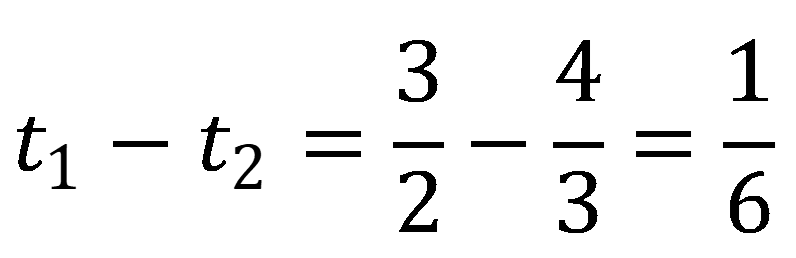
小时，即10分钟。

故正确答案为B。

实例2

某宣讲团甲宣传员骑摩托车从红星村出发以20公里/小时的速度去相距60公里的八一村，1小时后由于路面湿滑，速度减少一半，在甲出发1小时后，乙宣传员以50公里/小时的速度开车从红星村出发追甲，当乙追上甲时，他们与八一村的距离为（ ）

A. 25公里 B. 40公里 C. 35公里 D. 30公里

解析

根据题意，甲以20公里/小时的速度，走了一个小时，走过的距离为20公里，之后甲的速度变为10公里/小时，且乙以50公里/小时的速度追甲，属于直线追及运动，可列：20=(50-10)t，解得t=0.5，此时甲乙具八一村的距离为60-50×0.5=35公里。

故正确答案为C。

实例3

甲、乙、丙、丁四人同时同地出发，绕一椭圆环形湖栈道行走，甲顺时针行走，其余三人逆时针行走，已知乙的行走速度为60米/分钟，丙的速度为48米/分钟，甲在出发6、7、8分钟时分别与乙、丙、丁三人相遇，求丁的行走速度是多少?（ ）

A.31米/分钟 B.36米/分钟 C.39米/分钟 D.42米/分钟

解析

考察环形相遇问题：S=(v1+v2)·t，

S=6×(V甲+V乙)=7×(V甲+V丙)=8×(V甲+V丁)

→6×(V甲+60)=7×(V甲+48)，得V甲=24 米/分钟，

7×(24+48)=8×(24+V丁)，得V丁=39 米/分钟。

设甲的速度为v，椭圆形环湖栈道长度为s，根据环形相遇公式，则可得椭圆形环湖栈道长度为504米，甲的速度为24米/分钟。设丁的速度为h，根据环形相遇公式，504=(24+h)×8，可得h=39。

故正确答案为C。

考点二

工程问题

（一）核心公式

工作总量=工作效率×工作时间

注：

① 当工作效率一定的情况下，工作总量与工作时间呈正比例;

② 当工作时间一定的情况下，工作总量与工作效率呈正比例;

③ 当工作总量一定的情况下，工作时间与工作效率呈反比例。

（二）高频考法题干特征

1. 给定时间型：题目中只给定不同主体的完工时间，其余量未知。

2. 效率制约型：题目中不仅给定工作时间，还给出效率的比例倍数关系。

（三）解题思路：赋值法

1. 给完工时间

① 赋总量（完工时间的公倍数）

② 算效率：效率=总量÷时间

③ 根据工作过程列方程

完工时间：一次性完成全部工作所需的时间

2. 给效率比例

① 赋效率（满足比例即可）

② 算总量：效率×时间=总量

③ 根据工作过程列方程

3. 条件综合型

这一类区别于前两个题型，题目中关于工程问题公式的三个量给了两个或两个以上的时候，条件较多的工程问题，那么就利用工作总量不变列方程解答即可。

实例1

为支持“一带一路”建设，某公司派出甲、乙两队工程人员出国参与一个高铁建设项目。如果由甲队单独施工，200天可完成该项目;如果由乙队单独施工，则需要300天。甲、乙两队共同施工60天后，甲队被临时调离，由乙队单独完成剩余任务，则完成该项目共需（ ）天。

A. 120 B. 150 C. 180 D. 210

解析

第一步，本题考查工程问题，属于时间类。

第二步，赋值工作总量为时间（200天、300天）的公倍数600，则甲的效率是600÷200=3，乙的效率是600÷300=2。

第三步，甲、乙两队共同施工60天后，还剩余工作量为600-(2+3)×60=300。则乙队单独完成需要300÷2=150(天)，完成该项目共需60+150=210(天)。

故正确答案为D。

实例2

A、B、C三个工程队负责甲、乙两段工程相同性质的施工，现在先安排3个队伍进行5天甲段工程施工后，调A队伍去做乙段工程，8天后恰好同时完成，已知3个工程队效率之比为5:3:4，如果先安排3个队伍先做甲段，中间调C队去做乙段，也能同时完成，则C队是在工程开始后第（ ）天开始乙段工程。

A. 2 B. 3 C. 4 D. 5

解析

第一步，赋ABC三个队的效率分别为5、3、4。

第二步，求总量，甲乙两段工程性质相同，根据“先安排3个队伍进行5天甲段工程施工后，调A队伍去做乙段工程，8天后恰好同时完成”可以算出甲工作总量为（5+3+4）×5+(3+4)×8=116，乙的工作总量为5×8=40。

第三步分析求解，调C队去做乙，共需要40÷4=10天，即C队被调走后10天完成甲工程，则之前做了116-(5+3)×10=36，这36的工作量是三个人一起做的，共36÷(5+3+4)=3天，故第四天开始乙段工程。

故正确答案为C。

实例3

某工程队计划每天修路560米，恰好可按期完成任务。如每天比计划多修80米，则可以提前2天完成，且最后1天只需修320米。问如果要提前6天完成，每天要比计划多修多少米?（ ）

A. 160 B. 240 C. 320 D. 400

解析

第一步，本题考查工程问题。

第二步，设原计划修路时间为t天，可列方程：560t=(560+80)×(t-3)+320，解得t=20，可得修路总长度为560×20=11200(米)。

第三步，要想时间提前6天完成，即20-6=14(天)完成，则每天共需修路11200÷14=800(米)，那么比原计划每天多修800-560=240(米)。

故正确答案为B。

考点三

奇偶特性

1. 奇偶特性：加减法

奇数±奇数=偶数 偶数±偶数=偶数

奇数±偶数=奇数 偶数±奇数=奇数

2. 奇偶特性：乘法

奇数×奇数=奇数 偶数×偶数=偶数

奇数×偶数=偶数 偶数×奇数=偶数

3. 奇偶特性：总结

两个数做加减，结果是偶数，则这两个数必同奇同偶；

两个数做加减，结果是奇数，则这两个数必一奇一偶。

多个数做乘法，结果是偶数，则这些数中至少有一个数是偶数；

多个数做乘法，结果是奇数，则这些数中至少有一个数是奇数。

4. 主要题型

①已知和求差

②已知差求和

③不定方程

实例1

超市将99个苹果装进两种包装盒，大包装盒每个装12个苹果，小包装盒每个装5个苹果，共用了十多个盒子刚好装完。问两种包装盒相差多少个?（ ）

A. 3 B. 4 C. 7 D. 13

解析

第一步：识别题型，本题通过设大盒x 个，小盒y 个，得到12x+5y=99；判定此题列式为不定方程，因此考虑使用奇偶特性解题。第二步：审题找已知，根据12x+5y=99且5y 的尾数只能为0 或5，因此12x 的尾数只能为9 或4，且12x 为偶数。又有99为奇数，则5y一定是奇数。第三步：推算寻未知，5y 的尾数只能为5，12x的尾数只能4，可得x=2，y=15，相差13个，选择D选项。

故正确答案为D。

实例2

方程 px+q=99 的解为 x=1，则 p×q 的值为（ ）

A. 194 B. 197 C. 135 D. 155

解析

由题意可知p+q=99，一个方程是解不出p,q的具体值的，想求p×q的值，得从其他思路着手。利用奇偶特性，p+q=奇数，则p,q必是一奇一偶，那么p×q就必是偶数。观察选项，则选择A。

故正确答案为A。

实例3

某老旧写字楼重新装修，需要将原有的窗户全部更换为单价 90 元的新窗户，已知每 7 扇换下来的旧窗户可以跟厂商兑换一个新窗户，全部更换完毕后共花费 16560 元且剩余 4 扇旧窗户没有兑换，那么该写字楼一共有多少扇窗户?（ ）

A. 214 B. 218 C. 184 D. 188

解析

方法一：根据题意，设一共有X扇窗户，列方程有(X-4)/7+16560/90=X,解方程得X=214。

方法二：上面一种方法所列的方程是不容易解的，我们可以用奇偶特性来解这道题。根据题意，由“每 7 扇换下来的旧窗户可以跟厂商兑换一个新窗户，剩余4扇旧窗户没有兑换“，我们可知总的窗户数减4的结果是7的倍数，观察选项，则选A选项。

故正确答案为A。

考点四

经济利润问题

（一）基本公式

利润=售价-进价（进价即成本）

利润率=利润÷进价=（售价-进价）÷进价

售价=进价×（1+利润率）

折扣=售价÷定价；打几折，就在定价（原价）的基础上乘以零点几就是售价

总售价=单价×销售量

总利润=单件利润×销售量

（二）常考题型

1. 基本公式类

解决此类问题，拿到题目后迅速找到所用基本公式，代入给定数据，层层进行。

2. 分段计费类

分段计费，顾名思义，花费按段来收，段是什么，包括时间段，价格段，人数额度限制等。日常生活中常见的水电计费、出租车打车计费等等都属于分段计费问题。

解决关键在于找到分段节点，分区间讨论计算。

3. 统筹优化类

经济利润统筹类是指题目中问最小费用或者最大利润等经济利润与最值结合的问题。目的是以最少的钱买最多的东西，那就怎么便宜怎么买。

实例1

某商品成本为200元，售价为292元，公司根据市场情况调整了销售方案，将售价调整为268元，预计日销量将上涨15%。现欲通过改进生产线降低成本，以保持降价前的单日利润，则单件产品的生产成本至少需要降低（ ）。

A. 4% B. 5% C. 6% D. 8%

解析

第一步，本题考查经济利润问题。第二步，根据题意可列下表：

根据降价后保持降价前的单日利润，可得9200=115×(268-x)，解得x=188，成本降低了12元，降低了12÷200=6%。

故正确答案为C。

实例2

某学校组织学生春游，往返目的地时租用可乘坐10名乘客的面包车，每辆面包车往返的租金为250元。此外，每名学生的景点门票和午餐费用为40元，如要求尽可能少租车，则以下哪个图形最能反映平均每名学生的春游费用支出与参加人数之间的关系?（ ）

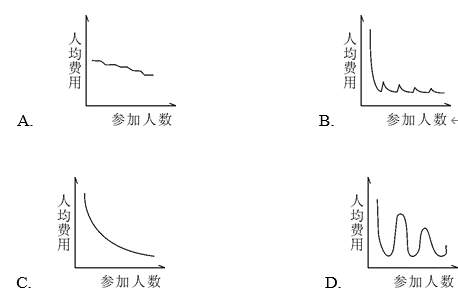
解析

看选项发现是最近两年比较新颖的题型-图形题。图表示的是人均费用与参加人数之间的关系。所以返回题干找两者的有关信息。发现，一辆面包车只够10个人来坐，从极端情况考虑，就坐1个人，人均车费是250/1=250元，但题中问的是平均每名学生的春游费用支出，也包括每名学生的景点门票和午餐费用40元，所以总的人均费用(纵坐标)为250+40=290元。假设坐10个人，同样的解答思路可得：人均费用为25+40=65元。

我们发现，当人数从1增加到10时，人均费用由290减少到65元，所以在图示上反映的话是一个急速下降的状态，A选项直接排除。

再来看，当有11个人时，另外要再租一辆车，总的出租费用250+250=500元，故人均费用为：500/11+40，约等于85元。由此可见，人均费用从65元又有一个小的回升，到85元。答案直接锁定B选项。

故正确答案为B。

实例3

某超市销售“双层锅”和“三层锅”两种蒸锅套装,其中“双层锅”需要2层锅身和1个锅盖,“三层锅”需要3层锅身和1个锅盖,并且每卖一个“双层锅”获利20元,每卖一个“三层锅”获利30元,现有7层锅身和4个锅盖来组合“双层锅”和“三层锅”两种蒸锅套装,那么最大获利为（ ）元。

A. 50 B. 60 C. 70 D. 80

解析

问的是最大获利，那么就要想办法把锅身锅盖尽可能全卖出去。分析题目，一个“双层锅”需要2层锅身，获利20元;一个“三层锅”需要3层锅身，获利30元。那么可以得出结论，一个锅身就可获利10元。现在有7个锅身，则尽可能都卖出去，就可以得到最大获利。不要忽略一个前提，4个锅盖一定得够用。

分情况来讨论：

a.卖出3个双层锅，需要6个锅身，3个锅盖，获利60元。

b.卖出2个三层锅，需要6个锅身，2个锅盖，获利60元。

c.卖出2个双层锅，1个三层锅，正好配成7个锅身，此时获利70元。再观察锅盖，用了3个锅盖，没有超额。

综上，最大获利是70元。

故正确答案为C。

考点五

几何最短路径问题

（一）题型

最短路径问题考查形式通常为求点之间的最短距离，核心解题方法为平面上两点之间，线段最短。在考试中最短路径问题主要分为平面几何最短路径与立体几何最短路径。

（二）平面几何最短路径

1. 两点异侧

题型特征：求在直线异侧的两点之间的最短距离，或在直线异侧的两点到第三点的最短距离之和。

解题方法：两点之间，线段最短，三点共线时距离之和最短。

2. 两点同侧

题型特征：求在直线同侧的两点到第三点的最短距离之和。

解题方法：将其中一点镜像对称，使三点共线。

（三）立体几何最短路径

题型特征：求立体图形中两点的最短距离

解题方法：将立体图形展开放在同一平面，连线计算

实例1

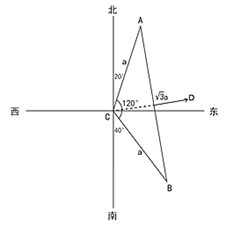
火车站A和B与初始发车站C的直线距离都等于akm，站点A在发车站C的北偏东20度，站点B在发车站C的南偏东40度，若在站点A和站点B之间架设火车轨道，则最短的距离为（ ）

A. a km B. 3a km C. 2a km D. √3a km

解析

如图所示，根据题意中A在C点北偏东20度和B在C点南偏东40度可知，A、B、C三点构成顶角为120度的等腰三角形，且AB为底边。过点C做AB的中垂线，交AB于点D。根据勾股定理可得，

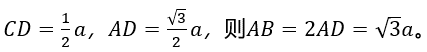
故正确答案为D。

实例2

A、B点和墙的位置如图所示。现从A点出发以5米/秒的速度跑向墙，接触到墙后再跑到B点。问最少要多少秒到达B点?（ ）

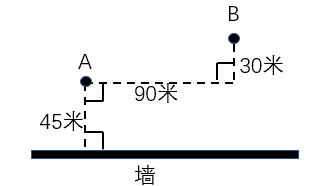
A. 30 B. 34 C. 38 D. 42

解析

要用最短时间到达B点，在速度一定的情况下，需从A接触到墙后再跑到B点所走的路程最短。如图，由于A和B在墙的同侧，可考虑做其中一个点关于墙的对称点，该对称点与另一个点的连线即为最短路程。假设做A点的对称点C，最短距离为BC。CD=90米，BD=30+45+45=120米，最短距离

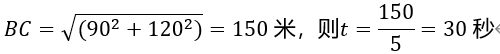
，故正确答案为A。

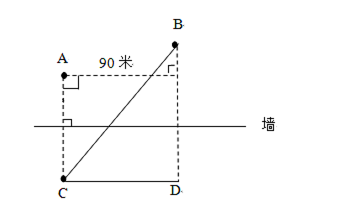
【先判断为同侧问题，需要作其中一点的对称点，再连接另外一点，用勾股定理求解。两点同侧时，对称哪一个点都可以，但是一般为了计算方便，建议对称短的那一个。】

实例3

长、宽、高分别为12cm、4cm、3cm的长方体ABCD-A1 B1 C1 D1上，有一个蚂蚁从A出发沿长方体表面爬行到C1获取食物，其路程最小值是多少cm?（ ）

A. 13 B. √193 C. √241 D. 17

解析

由题干蚂蚁从A出发沿长方体表面爬行到C1，求AC1最短。画图可知，在长方体中A和C1不在同一平面，要求最短距离先要把A和C1放在同一平面内，则把面CDC1D1翻折，形成面ABC1D1，再连接AC1，根据两点之间直线最短求解。如下图：

AC1是直角三角形ABC1的斜边，要让斜边最短，则两直角边的平方和要尽可能小。当AB=12，BC1=4+3=7时，两直角边的平方和最小，AC1最短=

故正确答案为B。

【长方体最短路径问题可直接运用结论，长方体中相对的两个顶点沿表面走的最短距离为：

；最短路径数为2条，因为长方体存在对立面，每一条路径都有一条与之相对的路径，因此有2条。】

考点六

容斥问题

（一）简述

容斥问题是一种计数的数学问题。容斥原理的基本思想是：先不考虑重复的数据，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复。

容斥问题有两种解题方法：

1. 画图法：可以解决所有的容斥问题。（注意画图时由里到外标数，剔除重复）

2. 公式法：可以解决一部分基础的容斥问题。

（二）二集合容斥问题

1. 画图法

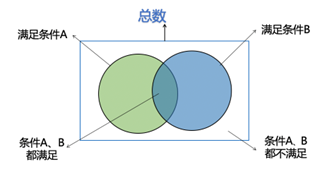
2. 二集合公式

总数=满足条件A+满足条件B-条件A、B都满足+条件A、B都不满足

（三）三集合容斥问题

1. 画图法

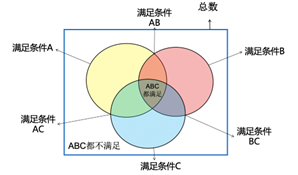
2. 三集合公式

① 标准型：

总数=满足条件A+满足条件B+满足条件C-满足条件AB-满足条件AC-满足条件BC+条件ABC都满足+条件ABC都不满足

② 变形公式1：

总数=A+B+C-满足两个条件-2×满足三个条件+ABC都不满足

③ 变形公式2：

总数=满足一个条件+满足两个条件+满足三个条件+ABC都不满足

实例1

市电视台向150位观众调查前一天晚上甲、乙两个频道的收视情况，其中108人看过甲频道，36人看过乙频道，23人即看过甲频道又看过乙频道，则接受调查观众中在前一天晚上两个频道均未看过的人数是（ ）

A. 17 B. 22 C. 29 D. 38

解析

本题考查容斥问题中的二集合容斥问题，题干中明确已知满足条件A，满足条件B，条件A、B都满足的数据，直接采用公式法，将已知条件带入到公式中即可解题。

设受调查观众在前一天晚上两个频道均未看过的人数为x，根据二集合容斥公式可列方程：150=108+36-23+x，解得x=29。

故正确答案为C。

实例2

有关部门对120种抽样食品进行化验分析，结果显示，抗氧化剂达标的有68种，防腐剂达标的有77种，漂白剂达标的有59种，抗氧化剂和防腐剂都达标的有54种，防腐剂和漂白剂都达标的有43种，抗氧化剂和漂白剂都达标的有35种，三种食品添加剂都达标的有30种，那么三种食品添加剂都不达标的有多少种?（ ）

A. 16 B. 17 C. 18 D. 19

解析

本题考查容斥问题中的三集合容斥问题，可直接采用三集合容斥公式解题。设三种食品添加剂都不达标的有x种，带入三集合容斥公式，列出方程：120=68+77+59-54-43-35+30+x，解得x=18。

故正确答案为C。

实例3

某乡镇举行运动会，共有长跑、跳远和短跑三个项目。参加长跑的有49人，参加跳远的有36人，参加短跑的有28人，只参加其中两个项目的有13人，参加全部项目的有9人。那么参加该次运动会的总人数为多少?（ ）

A. 75 B. 82 C. 88 D. 95

解析

第一步，本题考查容斥问题，属于三集合容斥类。第三步，运用画图法如下图所示即总体的数量x=49+36+28-13-2×9，解得x=82。

故正确答案为B。

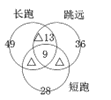
【画图标数的时候要注意只符合两种类型的区域，在图中总共有3个小区域，在这里可以标上符合△，表示△区域总面积为只符合两种类型的总数量，比如此题中的“只参加其中两个项目的有13人”。同时，这道题并没有给出都不符合的条件，故不需要画出最外边的方框】

考点七

排列组合问题

（一）基本原理与公式

1. 分类计数原理（加法原理）：

做一件事，有n类办法，在第1类办法中有m1种不同的方法，在第2类办法中有m2种不同的方法，…，在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+…+mn种不同的方法。

2. 分步计数原理（乘法原理）：

完成一件事，需要分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法，…，做第n步有mn种不同的方法，那么完成这件事共有N=m1×m2×⋯×mn种不同的方法。

3. 排列问题：

从n个不同元素种取出m(m≤n)个元素的所有不同排列的个数，叫做从n个不同元素种取出m个元素的排列数，用符号

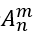
表示。

公式：

4. 组合问题：

从n个不同元素种取出m(m≤n)个元素的所有不同组合的个数，叫做从n个不同元素种取出m个元素的组合数，用符号

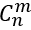
表示。

公式：

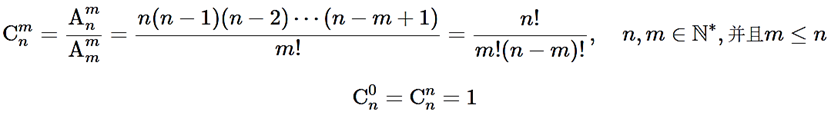
（二）经典解题方法

1. 捆绑法

当题目中要求元素必须相邻时，可将必须相邻元素捆绑在一起看成一个整体，再进行排列。注意：捆绑在一起的元素需要考虑其内部顺序。

2. 插空法：处理不相邻问题

当题目中要求元素必须不相邻时，可先将其他元素排好，再将不相邻的元素放到其他元素形成的空中。

3. 插板法：处理相同元素+不同分组每组至少存在x个

n个相同的物品分给m人，每人至少分1个，有

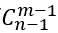
种不同的分法。

基本题型为：n个相同元素，不同个m组，每组至少有一个元素；则只需在n个元素的n-1个间隙中放置m-1块隔板把它隔成m份，求共有多少种不同方法？

其解题思路为：将n个相同的元素排成一行，n个元素之间出现了（n-1）个空档，现在我们用（m-1）个“档板”插入（n-1）个空档中，就把n个元素隔成有序的m份，每个组依次按组序号分到对应位置的几个元素（可能是1个、2个、3个、4个、….），这样不同的插入办法就对应着n个相同的元素分到m组的一种分法，这种借助于这样的虚拟“档板”分配元素的方法称之为插板法。

4.错位排列

直接记忆：

实例1

从5名男生5名女生中选出4人，去参加培训，在选出的4人中至少有1名男生1名女生的情况数有多少种？（ ）

A.100 B.200 C.500 D.700

解析

分成三类：

共50＋100＋50＝200种。

故正确答案为B。

实例2

扶贫干部某日需要走访村内6个贫困户甲、乙、丙、丁、戊和己。已知甲和乙的走访次序要相邻，丙要在丁之前走访，戊要在丙之前走访，己只能在第一个或最后一个走访。问走访顺序有多少种不同的安排方式?（ ）

A.32 B.48 C.16 D.24

解析

首先由题意知，戊丙丁的前后顺序已经固定，接着考虑己，己有2种选择（要么第一个，要么最后一个），甲乙先捆绑后插空，有4种选择，内部顺序有2种选择，所以共有2×4×2=16(种)。

故正确答案为C。

实例3

某单位组织志愿者参加公益活动，有8名员工报名，其中2名超过50岁。现将他们分成3组，人数为3、3、2，要求2名超过50岁的员工不在同组，则不同分组的方案共有（ ）种。

A.120 B.150 C.160 D.210

解析

第一步，本题考查排列组合问题，属于基础排列组合。

第二步，根据要求2名超过50岁的员工不在同组，有以下2种情况：

第三步，不同分组的方案共有90＋120＝210（种）。

故正确答案为D。

考点八

概率问题

（一）基本概念与公式

1. 概念：概率指的是一件随机事件发生的可能性或机率的度量，是一个在0到1之间的实数。

2. 公式：概率=满足条件的情况数÷总情况数

（二）分类分步概率

分类分步计数原理是解决排列组合问题的核心知识，而概率问题很多都需要应用排列组合知识解决。所以，“分类用加法，分步用乘法”同样适用于概率问题，具体如下：

分类概率：某项任务可以在多种情况下完成，则分别求解满足条件的每种情形的概率，然后将所有概率值相加。即：总体概率=满足条件的各种情况概率之和。

分步概率：某项任务必须按照多个步骤完成，则分别求解特定条件下每个步骤的概率，然后将所有概率值相乘。即：分步概率=满足条件的每个步骤概率之积。

（三）正难则反

如果一个概率问题，情况比较复杂，正面求解比较难，可以从反面着手解题，这样往往会取得意想不到的效果。即：正面概率=1-反面概率。

实例1

某高校从E，F和G三家公司购买同一设备的比例分别是20%，40%和40%，E，F和G三家公司所生产设备的合格率分别是98%，98%和99%，现随机购买到一台次品设备的概率是（ ）

A. 0.013 B. 0.015 C. 0.016 D. 0.01

解析

此题中E、F和G公司组成了某高校选购设备的一个整体，这可以从20%+40%+40%=100%看出来。所以此题应用的公式是分类概率，用加法。而三家公司所生产设备的合格率分别是98%，98%和99%，则我们不难得出，三家公司生产的次品率分别是：2%，2%，1%，所以，应用公式：随机购买到一台次品设备的概率=20%×2%+40%×2%+40%×1%=0.016

故正确答案为C。

实例2

小王开车上班需经过4个交通路口，假设经过每个路口遇到红灯的概率分别为0.1、0.2、0.25、0.4，则他上班经过4个路口至少有一处遇到绿灯的概率是（ ）

A. 0.899 B. 0.988 C. 0.989 D. 0.998

解析

此题采用正向思维的方式不好求解，我们不妨换个思维方式，至少一处遇到绿灯的概率，其对立面恰好是，全都遇到红灯。所以，4个路口至少有一处遇到绿灯的概率=1-0.1×0.2×0.25×0.4=1-0.002=0.998。

故正确答案为D。

考点九

倍数特性

（一）适用题型

1. 适用题型：倍数特性法一般应用于倍数问题，平均数问题，余数问题，比例关系问题，不定方程问题等题型，以及解方程的过程中。

2. 题干特征：当题干中出现分数、比例、倍数、整除等明显特征时，可考虑倍数特性法。

（二）基本理论

1. 特殊数字整除判定：

① 2/5整除：观察数字的末位数字能否被2/5整除。

② 4/25整除：观察数字的末两位数能否被4/25整除。

③ 8/125整除：观察数字的末三位数能否被8/125整除。

④ 3/9整除：观察各位数字之和能否被3/9/整除。例如，12375的各位数字和是18，能被3整除，故12375能被3整除。

2. 普通数字整除判定：

普通数字的整除判定，一般采用分解因式的方法进行快速判断。如判断一个数字能否被6整除，因6=2×3，则只需要判定该数能否被2和3整除；再如，判定531能否被47整除，可以将531分解为(470+61=47×10+61)，因61不能分解为含有47的因式，故531不能被47整除。

3. 分数比例形式整除：

若a∶b=m∶n（m、n互质），则a是m的倍数，b是n的倍数；

4. 与代入排除法的结合

倍数特性法解析，本质是在排除不符合的选项，因此需要与代入排除法相结合。

（三）适用题型及技巧

1. 平均数问题、倍数问题等

模型：a=mb型。

解题方法：a可被m整除，a可被m的约数整除

2. 余数类问题

模型：a=mb±n型

解题方法：a=mb+n，a-n可被m及其约数整除，a=mb-n，a+n可被m及其约数整除。

3. 型如

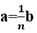
的题目

题型特征：题目出出现分数、百分数、比例、倍数等情况。

解题方法：b是n的倍数

4. 型如

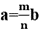
的题目

题型特征：题目出出现分数、百分数、比例、倍数等情况。

解题方法：若a∶b=m∶n(m、n互质)，则a是m的倍数，b是n的倍数；

5. 型如

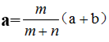
的题目

题型特征：题目出出现分数、百分数、比例、倍数等情况。

解题方法：

6. 因子特性

定义：“因子特性法”即利用式子中是否包含某些特定因子来进行答案的排除及选择的一种方法，其应用的核心在于“见到乘法想因子”。即“若等式一边包含某个因子，则等式另一边必然包括该因子。

实例1

某工厂生产的零件总数是一个三位数，平均每个车间生产了35个，统计员在记录时粗心地将该三位数的百位与十位数字对调，结果统计的零件总数比实际总数少270个。问该工厂所生产的零件总数最多可能有多少个?（ ）

A. 525 B. 630 C. 855 D. 960

解析

本题属于平均数问题。由“平均”每个车间生产35个，知总数能被35整除，排除C、D；根据零件总数“最多”，代入B选项，十位与百位“对调”，为360，“比”实际少了630-360=270个，符合要求。

故正确答案为B。

【判定一个数能否被35整除，只需判定这个数能否被5和7同时整除即可。】

实例2

车间领到一批电影票和球票发放给车间工人，电影票数是球票数的2倍。如果每个工人发3张球票，则富余2张，如果每个工人发7张电影票，则缺6张，问车间领到多少张球票?（ ）

A. 32 B. 30 C. 64 D. 60

解析

余数问题，球票总数减去2能被3整除，结合选项代入验证只有32满足。

故正确答案为A。

实例3

春风街道办事处为丰富老年人文化生活，准备举行老年人才艺活动，活动项目共有书法、绘画、歌曲演唱、太极拳四项。参加者报名项数不限、每种报名方式最多可报四人。经统计，共有三人同时报名参加书法和绘画项目。据此，参加老年才艺秀活动最多报名（ ）人。

A. 68 B. 73 C. 45 D. 47

解析

设剔除同时报名了书法和绘画项目的方式后有x种方式，可知最多报名人数为(4x+3)人。即答案-3能被4整除。只有D选项满足。

故正确答案为D。

【本题可转化为a=mb+n的形式，按照余数问题的倍数特性解题技巧去求解。】

实例4

某企业共有职工100多人，其中，生产人员与非生产人员的人数之比为4︰5，而研发与非研发人员的人数之比为3︰5。已知生产人员不能同时担任研发人员，则该企业不在生产和研发两类岗位上的职工有多少人?（ ）

A. 20 B. 30 C. 24 D. 26

解析

实例5

小张的孩子出生的月份乘以29，出生的日期乘以24，所得的两个乘积加起来刚好等于900。问孩子出生在哪一季度?（ ）

A. 第一季度 B. 第二季度 C. 第三季度 D. 第四季度

解析

设出生月份为x，出生日期为y。根据刚好“等于”900可得，29x+24y=900。由于24与900都能被12整除，则29x也能被12整除，故x必能被12整除。因x表示月份，故x=12，即第四季度。

故正确答案为D。

考点十

代入排除法

（一）适用题型

1. 特定题型：多位数问题、年龄问题、余数问题、不定方程等。

2. 选项信息充分：选项为一组数；选项可以转化为一组数。

3. 其他情况：条件特复杂；代入排除后只剩两项答案可选。

（二）基本原则

1. 符合题干当中全部条件即为正确答案，符合题干当中部分条件则待定，因为符合部分条件不一定是正确答案，但不符合部分条件一定是错误答案。

2. 求大代大，求小代小。

3. 容易算的选项或条件优先带入。

4. 题目必须是求取具体数值，而不是求倍比关系等结果。

5. 当选项有多个数值时，更适合使用代入排除法，可以较为方便的进行验证。

实例1

在公司的年会表演中，有甲、乙、丙、丁四个部门的员工参演。已知甲、乙两部门共有16名员工参演，乙、丙两部门共有20名员工参演，丙、乙两部门共有34名员工参演。且各部门参演人数从多到少的顺序为：甲<乙<丙<丁。由此可知，丁部门有多少人参演？（ ）

A. 16 B. 20 C. 23 D. 25

解析

此题仅给了数量之和，并且给了甲、乙、丙、丁的排列顺序，属于无法直接从正面入手的题型，优先采用代入排除法，将A选项丁部门人数16代入题目，反推出丙18人，乙2人，甲14人，不满足各部门人数的大小关系，排除；同理可排除B、D，因此选C。

故正确答案为C。

实例2

小李的弟弟比小李小2岁，小王的哥哥比小王大2岁、比小李大5岁。1994年，小李的弟弟和小王的年龄之和为15。问2014年小李与小王的年龄分别为多少岁?（ ）

A. 25，32 B. 27，30 C. 30，27 D. 32，25

解析

此题求小李与小王的年龄，题目中表达两者年龄关系的条件为“小王的哥哥比小王大2岁、比小李大5岁”可知，小王比小李大三岁，带入选项不难发现，只有B满足。

故正确答案为B。

实例3

一个五位数，左边三位数是右边两位数的5倍，如果把右边两位数移到前面，所得到的新的五位数要比原来的五位数的2倍还多75，原来五位数的值是多少?（ ）人。

A. 22545 B. 17535 C. 12525 D. 11575

解析

第一步，本题考查多位数问题。 第二步，多位数问题优先考虑使用代入排除法。代入A选项，225÷45=5，22545×2+75=45165，不符合题意，排除;同理，代入BCD选项，只有C选项完全符合题意(125÷25=5，12525×2+75=25125)。

故正确答案为C。