C++进阶之路---手把手带你学习AVL树

顾得泉：个人主页

个人专栏：《Linux操作系统》 《C++从入门到精通》  《LeedCode刷题》

键盘敲烂，年薪百万！

---

一、AVL树的概念

       二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：

       当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

       一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

       1.它的左右子树都是AVL树

       2.左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

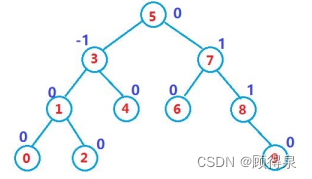
       如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在(log_2 n)，搜索时间复杂度O(log_2 n)。 

---

二、AVL树的旋转

       如果在一颗原本平衡的AVL树插入新节点后，平衡因子可能会发生变化，从而使绝对值大于1，所以就需要旋转去调整树的结构，使之平衡化，而根据节点的不同，旋转就有4中情况。

1.左单旋

实现图解：

代码实现：

void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
 
	parent->_right = subRL;
	subR->_left = parent;
 
	Node* parentParent = parent->_parent;
 
	parent->_parent = subR;
	if (subRL)
		subRL->_parent = parent;
 
	if (_root == parent)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (parentParent->_left == parent)
		{
			parentParent->_left = subR;
		}
		else
		{
			parentParent->_right = subR;
		}
		subR->_parent = parentParent;
	}
	parent->_bf = subR->_bf = 0;
}

2.右单旋

实现图解：

代码实现:

void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
 
	parent->_left = subLR;
	if (subLR)
		subLR->_parent = parent;
 
	Node* parentParent = parent->_parent;
 
	subL->_right = parent;
	parent->_parent = subL;
 
	if (_root == parent)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (parentParent->_left == parent)
		{
			parentParent->_left = subL;
		}
		else
		{
			parentParent->_right = subL;
		}
		subL->_parent = parentParent;
	}
	subL->_bf = parent->_bf = 0;
}

3.左右双旋

       将双旋变成单旋后再旋转，即:先对30进行左单旋，然后再对90进行右单旋，旋转完成后再考虑平衡因子的更新。

实现图解：

代码实现:

void RotateLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	int bf = subLR->_bf;
 
	RotateL(parent->_left);
	RotateR(parent);
 
	if (bf == 0)
	{
		// subLR自己就是新增
		parent->_bf = subL->_bf = subLR->_bf = 0;
	}
	else if (bf == -1)
	{
		// subLR的右子树新增
		parent->_bf = 0;
		subLR->_bf = 0;
		subL->_bf = 1;
	}
	else if (bf == 1)
	{
		// subRL的左子树新增
		parent->_bf = -1;
		subLR->_bf = 0;
		subL->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

4.右左双旋

       具体实现参考左右双旋。

实现图解：

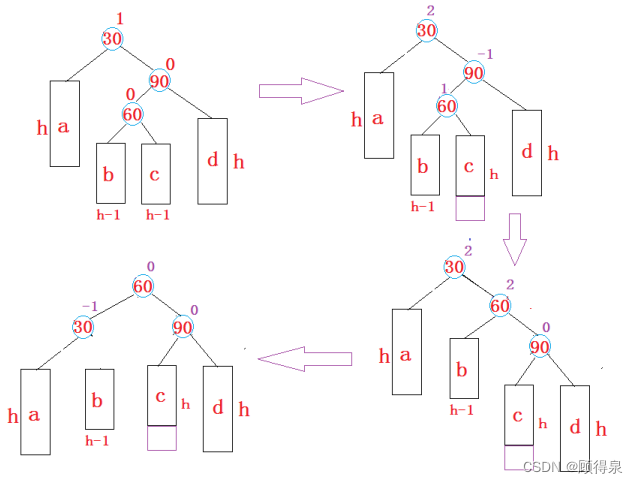
代码实现：

void RotateRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int bf = subRL->_bf;
 
	RotateR(parent->_right);
	RotateL(parent);
 
	if (bf == 0)
	{
		// subRL自己就是新增
		parent->_bf = subR->_bf = subRL->_bf = 0;
	}
	else if (bf == -1)
	{
		// subRL的左子树新增
		parent->_bf = 0;
		subRL->_bf = 0;
		subR->_bf = 1;
	}
	else if (bf == 1)
	{
		// subRL的右子树新增
		parent->_bf = -1;
		subRL->_bf = 0;
		subR->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

5.旋转总结 

---

三、AVL树的基本实现

1.AVL树的节点实现

template<class K, class V>
struct AVLTreeNode
{
    AVLTreeNode<K, V>* _left;
    AVLTreeNode<K, V>* _right;
    AVLTreeNode<K, V>* _parent;
    pair<K, V> _kv;
 
    int _bf; // balance factor
 
    AVLTreeNode(const pair<K, V>& kv)
        :_left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _kv(kv)
        , _bf(0)
    {}
};

2.AVL树的插入实现

class AVLTree
{
    typedef AVLTreeNode<K, V> Node;
public:
    bool Insert(const pair<K, V>& kv)
    {
        if (_root == nullptr)
        {
            _root = new Node(kv);
            return true;
        }
 
        Node* parent = nullptr;
        Node* cur = _root;
 
        while (cur)
        {
            if (cur->_kv.first < kv.first)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_kv.first > kv.first)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;
            }
        }
 
        cur = new Node(kv);
        if (parent->_kv.first < kv.first)
        {
            parent->_right = cur;
            cur->_parent = parent;
        }
        else
        {
            parent->_left = cur;
            cur->_parent = parent;
        }
 
        while (parent)
        {
            if (cur == parent->_left)
            {
                parent->_bf--;
            }
            else
            {
                parent->_bf++;
            }
 
            if (parent->_bf == 0)
            {
                break;
            }
            else if (parent->_bf == 1 || parent->_bf == -1)
            {
                cur = parent;
                parent = parent->_parent;
            }
            else if (parent->_bf == 2 || parent->_bf == -2)
            {
                if (parent->_bf == 2 && cur->_bf == 1)
                {
                    RotateL(parent);
                }
                else if (parent->_bf == -2 && cur->_bf == -1)
                {
                    RotateR(parent);
                }
                else if (parent->_bf == 2 && cur->_bf == -1)
                {
                    RotateRL(parent);
                }
                else if (parent->_bf == -2 && cur->_bf == 1)
                {
                    RotateLR(parent);
                }
 
                // 1、旋转让这颗子树平衡了
                // 2、旋转降低了这颗子树的高度，恢复到跟插入前一样的高度，所以对上一层没有影响，不用继续更新
                break;
            }
            else
            {
                assert(false);
            }
        }
 
        return true;
    }
private:
    Node* _root=nullptr;
};

---

四、AVL树的性能

       AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即log2n。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

---

预告：AVL树固然nb,但是红黑树更强！如果说发明AVL树的人是周瑜，那么发明红黑树的人就是诸葛亮。下篇文章带你学习红黑树。

---

结语：C++关于如何实现AVL树的分享到这里就结束了，希望本篇文章的分享会对大家的学习带来些许帮助，如果大家有什么问题，欢迎大家在评论区留言~~~