新手入门python实现神经网络，超级简单!_py 神经网络

前言：

这篇文章完全是为新手准备的。我们会通过用Python从头实现一个神经网络来理解神经网络的原理。

---

神经元

首先让我们看看神经网络的基本单位，神经元。神经元接受输入，对其做一些数据操作，然后产生输出。例如，这是一个2-输入神经元：

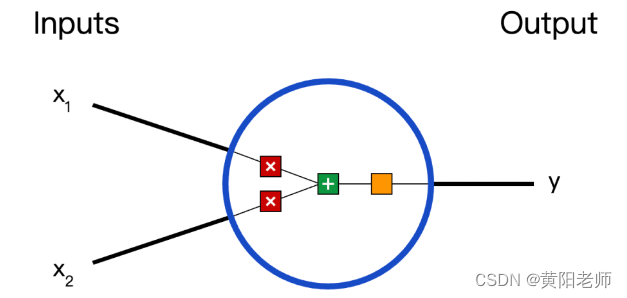
这里发生了三个事情。首先，每个输入都跟一个权重相乘（红色）：
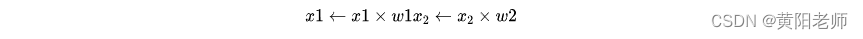然后，加权后的输入求和，加上一个偏差b（绿色）：

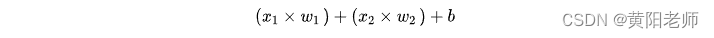
最后，这个结果传递给一个激活函数f：

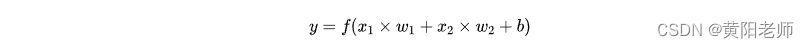
激活函数的用途是将一个无边界的输入，转变成一个可预测的形式。常用的激活函数就是S型函数：

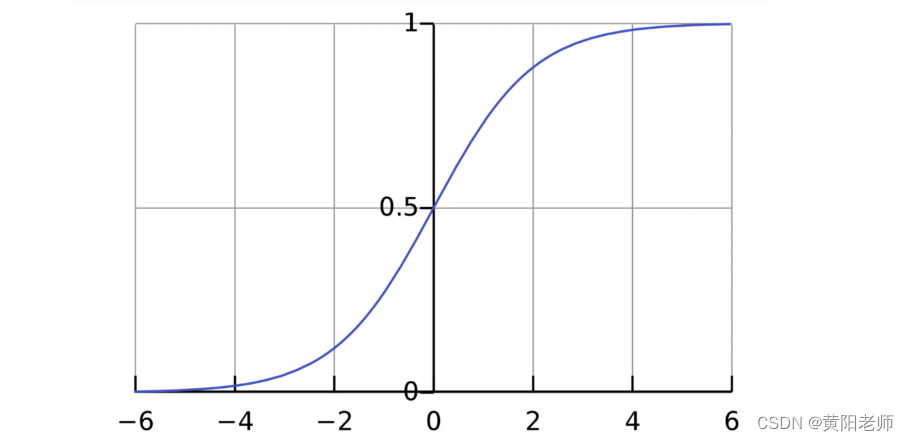
S型函数的值域是(0, 1)。简单来说，就是把(−∞, +∞)压缩到(0, 1) ，很大的负数约等于0，很大的正数约等于1。

1、一个简单的例子

2、编码一个神经元

让我们来实现一个神经元！用Python的NumPy库来完成其中的数学计算：

import numpy as np

def sigmoid(x):
  # 我们的激活函数: f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

class Neuron:
  def __init__(self, weights, bias):
    self.weights = weights
    self.bias = bias

  def feedforward(self, inputs):
    # 加权输入，加入偏置，然后使用激活函数
    total = np.dot(self.weights, inputs) + self.bias
    return sigmoid(total)

weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4                   # b = 4
n = Neuron(weights, bias)

x = np.array([2, 3])       # x1 = 2, x2 = 3
print(n.feedforward(x))    # 0.9990889488055994
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

还记得这个数字吗？就是我们前面算出来的例子中的0.999。

把神经元组装成网络

所谓的神经网络就是一堆神经元。这就是一个简单的神经网络：

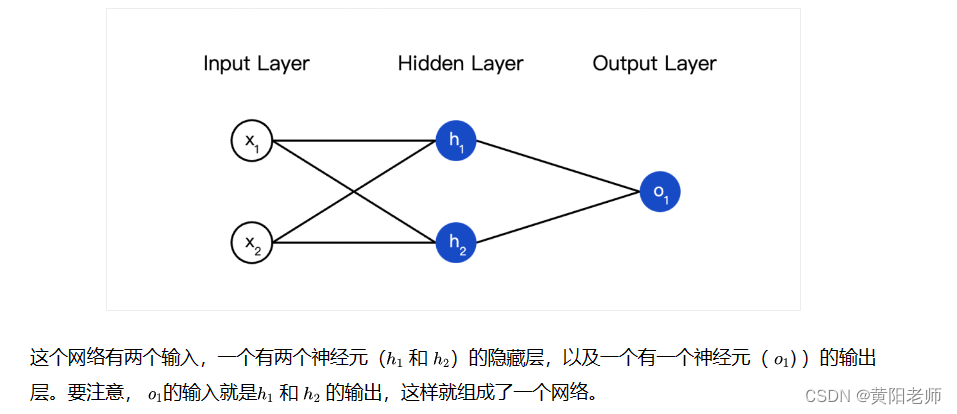
隐藏层就是输入层和输出层之间的层，隐藏层可以是多层的。

1、例子：前馈

2、编码神经网络：前馈

接下来我们实现这个神经网络的前馈机制，还是这个图：

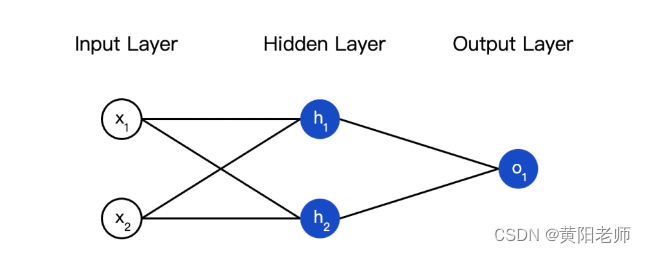
import numpy as np

def sigmoid(x):
# 我们的激活函数：f(x)=1/(1+e^(-x))
    return 1/(1+np.exp(-x))
# 单个神经元
class Neuron:
    def __init__(self,weights,bias):
        self.weights=weights
        self.bias=bias
    def feedforward(self,inputs):
        total=np.dot(self.weights,inputs)+self.bias
        return sigmoid(total)

class OurNeuralNetwork:
  '''
  A neural network with:
    - 2 inputs
    - a hidden layer with 2 neurons (h1, h2)
    - an output layer with 1 neuron (o1)
  Each neuron has the same weights and bias:
    - w = [0, 1]
    - b = 0
  '''
  def __init__(self):
    weights = np.array([0, 1])
    bias = 0

    # 这里是来自前一节的神经元类
    self.h1 = Neuron(weights, bias)
    self.h2 = Neuron(weights, bias)
    self.o1 = Neuron(weights, bias)

  def feedforward(self, x):
    out_h1 = self.h1.feedforward(x)
    out_h2 = self.h2.feedforward(x)

    # o1的输入是h1和h2的输出
    out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))

    return out_o1

network = OurNeuralNetwork()
x = np.array([2, 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43