- 1web基础漏洞之CSRF(跨站请求伪造漏洞)_cookie session token配置导致的漏洞
- 2Vue+ Electron 开发的一个跨三端的应用(Taro开发多端应用)
- 3《阿里工程师的自我修养》笔记_阿里工程师文化的精髓
- 4Elasticsearch教程(二)java集成Elasticsearch
- 5Gartner发2017技术成熟度曲线,和愈发明显的技术“小真空期”
- 6常见web应用防护软件下载2021_web终端防护软件
- 7中间件几百万消息持续积压及小时,怎么处理?_线上生产出现消息积压怎么办
- 8利用Android studio设计一个计算器_android studio 计算器
- 9java毕业设计成品源码网站基于ssm的NBA球队|篮球管理系统[包运行成功]_java成品网站
- 10华为数通配置旁挂二层组网直接转发实验
【数据可视化包Matplotlib】Matplotlib基本绘图方法
赞
踩
一、Matplotlib绘图的基本流程
根据 Matplotlib 图像的4层图像结构,pyplot 模块绘制图形基本都遵循一个流程,使用这个流程可以完成大部分图形的绘制。pyplot 模块基本绘图流程主要分为3个部分,如下图所示。

- 创建画布:plt.figure()
- 创建和选定子图:plt.subplots()
- 添加标题:plt.title()
- 添加x/y轴名称:plt.xlabel()、plt.ylabel()
- 设置x/y轴范围:plt.xlim()、plt.ylim()
- 设置x/y轴范围:plt.xticks()、plt.yticks()
- 绘制图形:折线图—plot()、柱状图—bar()、饼图—pie()、散点图—scatter()、箱型图—boxplot()
- 添加图例:plt.legend()
- 保存图形:plt.savefig()
- 显示图形:plt.show()——一般放在最后
在 Jupyter Notebook 中运行时需要加上下面这条魔法命令。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
- 1
- 2
- 3
(一)最简单的绘图(仅指定y的值)
用marker参数观察可知,绘图时使用列表的索引(0、1、2)作为x值,用列表值作为对应的y值(需要取消下一句的注释!)。
plt.plot([1,2,3])
# plt.plot([1,2,3],marker="o")
- 1
- 2
(二)更一般的绘图(同时指定x和y的值)
x = np.linspace(-2, 2, 20) # 产生20个坐标点的横坐标
y = x**2 # 产生20个坐标点的纵坐标
# 最简单的绘图
plt.rcParams['axes.unicode_minus']= False # 解决不显示负号的问题
plt.plot(x, y) # 默认不突出显示坐标点,坐标点之间用蓝色实线连接
plt.show() # 调用show()函数才真正显示图形
- 1
- 2
- 3
- 4
- 5
- 6
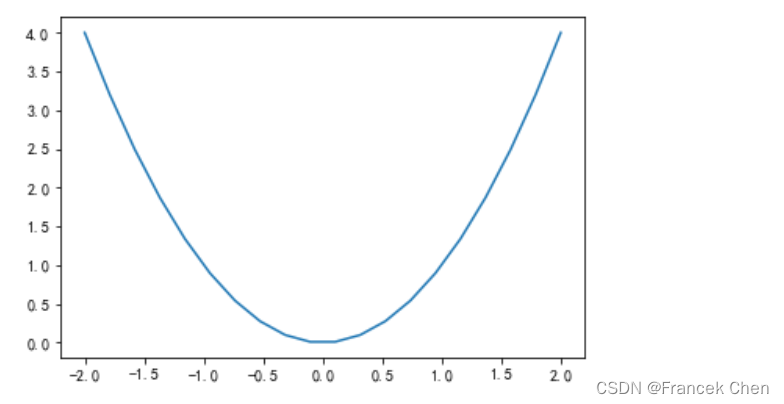
x = np.linspace(-2, 2, 20) # 产生20个坐标点的横坐标 y = x**2 # 产生20个坐标点的纵坐标 px = 0.8 # 靓点(Beautiful point)之横坐标 py = px**2 # 靓点之横坐标 plt.title("Square function") # 图表标题 plt.xlabel("x") # x轴标签 plt.ylabel("y = x**2") # y轴标签 plt.grid(True) # 显示网格线 plt.plot(x, y, "b*-.", px, py, "ro") # 同时指定连接线和坐标点的样式、颜色 # 添加文本说明,前两个参数表示第一个字符的横纵坐标,第3个参数是文本字符串。 # 字符串中的 $y=x^2$ 是Latex的等式表示形式 plt.text(0, 2, "Square function\n$y = x^2$", fontsize=20, color='blue', horizontalalignment="center") plt.text(px - 0.08, py, "Beautiful point", ha="right", weight="heavy") # ha即horizontalalignment plt.text(px, py, "x = %0.2f\ny = %0.2f"%(px, py), rotation=50, color='gray') plt.savefig("my_plot1.png") # 在当前目录下保存所绘制的图形 plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
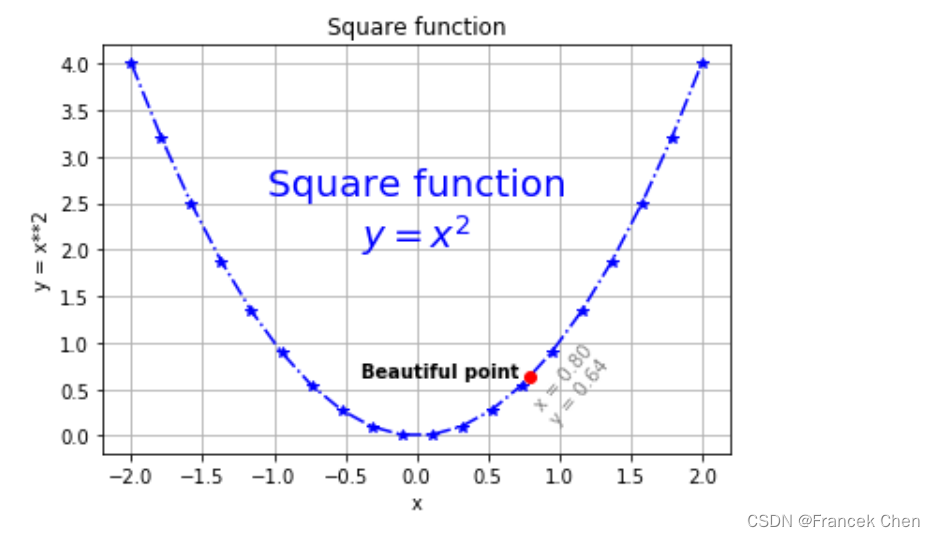
(三)增加更多的绘图元素
x = np.linspace(0,2*np.pi,13) # 数据点以pi/6(30度)作为分隔间距 y1 = np.sin(x) y2 = np.cos(x) plt.plot(x,y1,marker='^',color='r',label="sin(x)") # 默认线型是实线 plt.plot(x,y2,marker='o',color='g',linestyle='-.',label="cos(x)") # label参数和plt.legend()配合实现图例显示 plt.xlim(0,2*np.pi) # 设定x轴的取值范围 plt.ylim(-1,1) plt.xlabel("x") # 设定x轴的标签 plt.ylabel("y") plt.title("y=sin(x)/cos(x)") # 设定x轴的刻度,下一条语句可以注释对比一下效果, # 其中x[::3]的3表示经过3个数据点加一个标签,可以改成1看的更明显 plt.xticks(x[::3],["0",r"$\pi/2$",r"$\pi$",r"$3\pi/2$",r"$2\pi$"],color='b') # "$\pi/2$"属于Latex表示法 plt.grid(axis='x',ls='--') plt.legend() plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
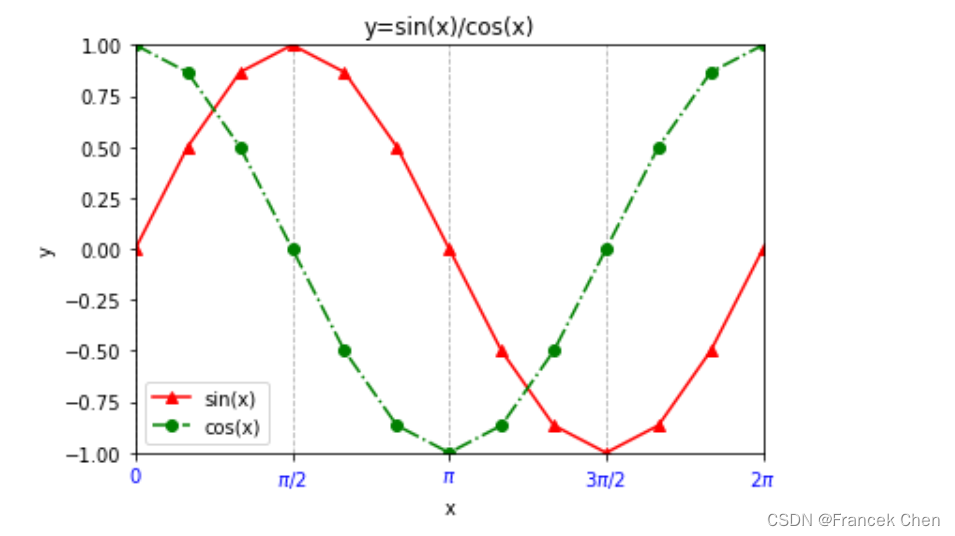
二、布局相关的对象——Figure、Subplot
# 创建自己的Figure对象,相当于自定义画布 #(通过注释下条语句,观察使用自己的Figure对象的效果) fig = plt.figure(figsize=(12,8)) # 指定画板的宽和高分别为12英寸和8英寸 # 上面语句可省略,如果省略就是使用系统内部默认的figure()对象 # 运行配置(run configuration)参数设置 plt.rcParams['font.sans-serif']=['SimHei'] # 在matplotlib中显示汉字 plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号,否则负号会显示为小方框 # 绘制子图 x = np.linspace(-2, 2, 30) plt.subplot(2, 2, 1) # 2 rows, 2 columns, 1st subplot = top left plt.plot(x, x) plt.subplot(2, 2, 2) # 2 rows, 2 columns, 2nd subplot = top right plt.plot(x, x**2) plt.subplot(2, 1, 2) # 2 rows, *1* column, 2nd subplot = bottom plt.plot(x, x**3) plt.text(0,-5,"看成按照2行1列重新划分的第2个子图",ha="center",color="red") # ha:horizontal align(水平对齐) plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19

三、常用图形绘制
(一)折线图
一般绘制较多的的都是折线图,反映一个特征随另一个特征的趋势变化。
rad = np.arange(0,np.pi*2,0.01)
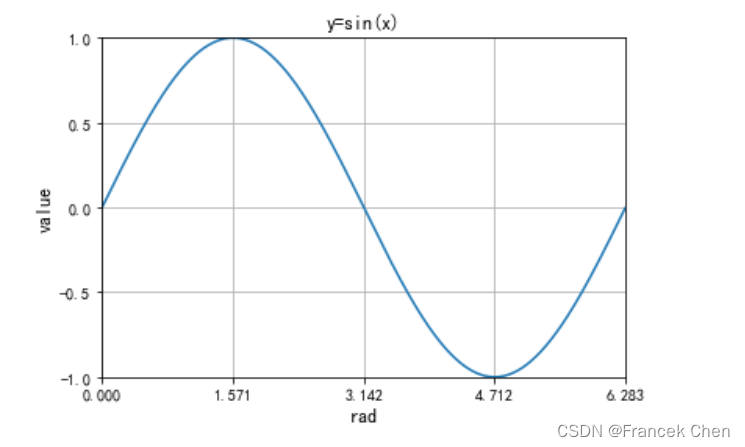
plt.title("y=sin(x)",fontsize=12)
plt.xlabel("rad",fontsize=12)
plt.ylabel("value",fontsize=12)
plt.xlim((0,np.pi*2))
plt.ylim((-1,1))
plt.xticks([0,np.pi/2,np.pi,np.pi*3/2,np.pi*2])
plt.yticks([-1,-0.5,0,0.5,1])
plt.grid(True)
plt.plot(rad,np.sin(rad))
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
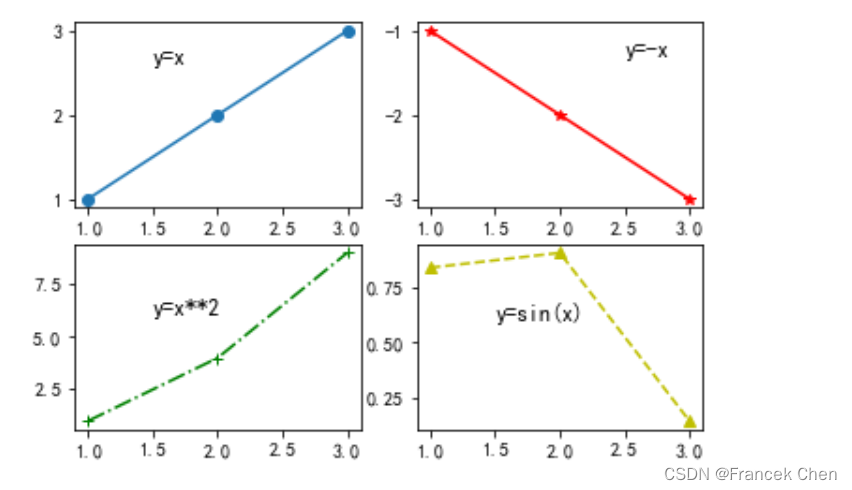
# 带子图的折线图
x = np.array([1,2,3])
plt.subplot(221)
plt.plot(x,x,marker="o")
plt.text(1.5,2.6,"y=x",fontsize=12)
plt.subplot(222)
plt.plot(x,-x,"-*r")
plt.text(2.5,-1.3,"y=-x",fontsize=12)
plt.subplot(223)
plt.plot(x,x**2,"-.+g")
plt.text(1.5,6.0,"y=x**2",fontsize=12)
plt.subplot(224)
plt.plot(x,np.sin(x),"--^y")
plt.text(1.5,0.6,"y=sin(x)",fontsize=12)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
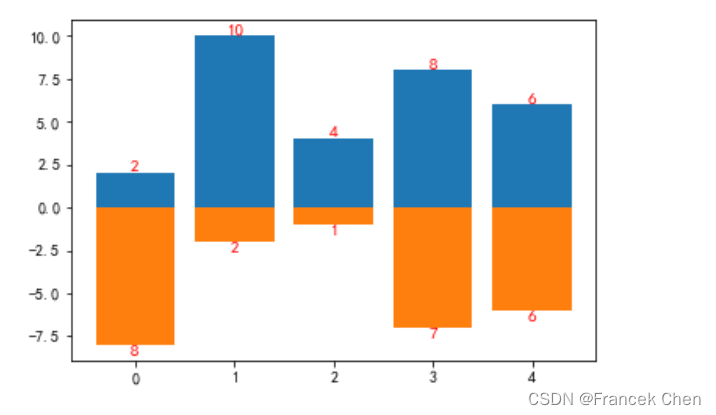
(二)柱状图
绘制柱状图,比较值大小。
position = np.arange(5) # 确定每个柱的垂直中线位置,相当于x轴坐标
data1 = [2,10,4,8,6] # 确定每个柱的高度,相当于y轴坐标
data2 = np.random.randint(1,9,5)#[5,3,6,7,6]
plt.bar(position,data1)
plt.bar(position,-data2)
for x, y in zip(position, data1): # 显示数据标签
plt.text(x, y, '{}'.format(y), ha='center', va='bottom',fontsize=11,color='r')
# va='bottom'表示文本的底部在(x,y)处,还可以取top和center值
for x, y in zip(position, data2): # 显示数据标签
plt.text(x, -y, '{}'.format(y), ha='center', va='top',fontsize=11,color='r')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
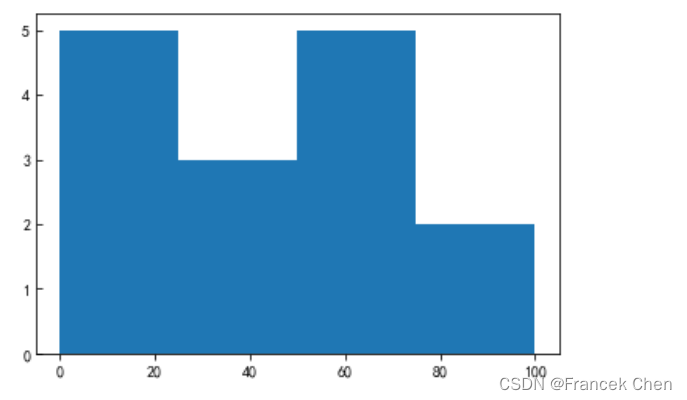
(三)直方图
绘制直方图,反映数据分布。
x = [22,87,5,43,56,73,55,54,11,20,51,5,79,31,27] # x轴数据
plt.hist(x, bins = [0,25,50,75,100]) # 绘制直方图,bins为区间
plt.show() # 显示图表
- 1
- 2
- 3
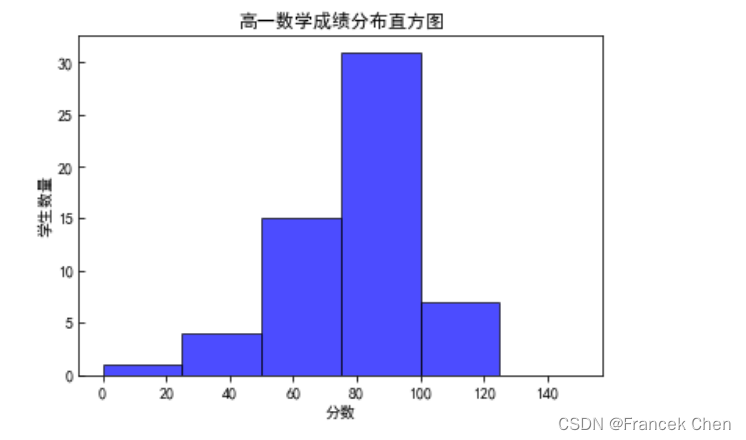
进一步拓展。
df = pd.read_excel('grade1.xls') # 读取Excel文件
plt.rcParams['font.sans-serif']=['SimHei'] # 解决中文乱码
x = df['得分'] # x轴数据
plt.xlabel('分数') # x轴标题
plt.ylabel('学生数量') # y轴标题
plt.title("高一数学成绩分布直方图") # 设置图表标题
# 绘制直方图,bins为区间,facecolor为前景色,edgecolor为边框颜色,alpha为透明度
plt.hist(x, bins = [0,25,50,75,100,125,150],facecolor="blue", edgecolor="black", alpha=0.7)
plt.show() # 显示图表
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
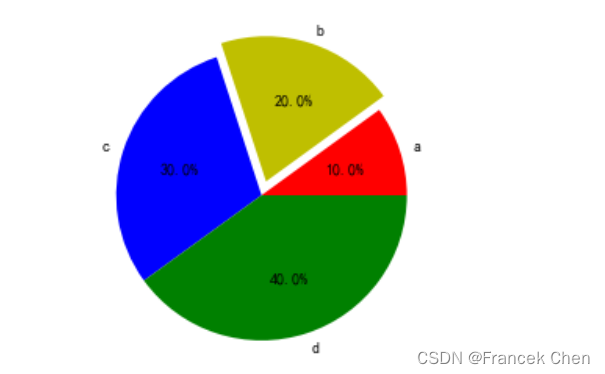
(四)饼图
绘制饼图,展示整体的构成情况。
x = [2,4,6,8]
labels = ['a','b','c','d'] # 各部分的标签
colors = ['r','y','b','g'] # 各部分的颜色
explode = (0,0.1,0,0) # explode用于突出显示特定的部分
# explode=(0.1,0.3,0.1,0.1)
plt.pie(x,explode=explode,labels=labels,colors=colors,autopct='%.1f%%') # pct表示percent,%%用于输出一个百分号
plt.axis("equal") ##使饼图两个轴的单位长度相等,从而使得饼图接近圆形
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
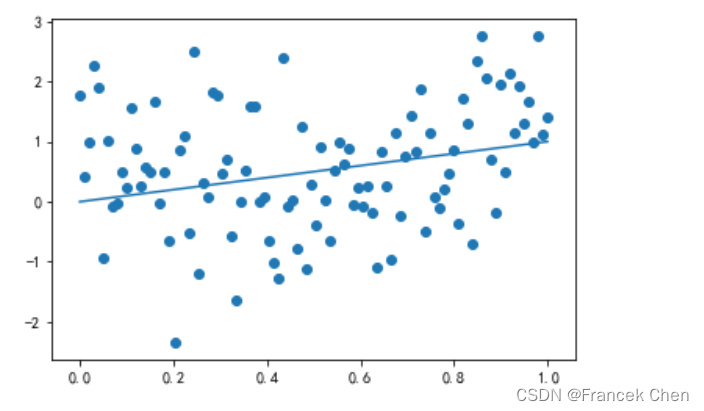
(五)散点图
绘制散点图,展示数据聚集模式、观察两个一维数据序列间的关系。
# 基本的常用于线性回归分析中
np.random.seed(0) # 作用相当于random.seed(),但它返回一个伪随机数生成器对象,可用该对象生成随机数
x = np.linspace(0,1,100)
y = x+np.random.randn(100)
plt.scatter(x,y)
plt.plot(x,x)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
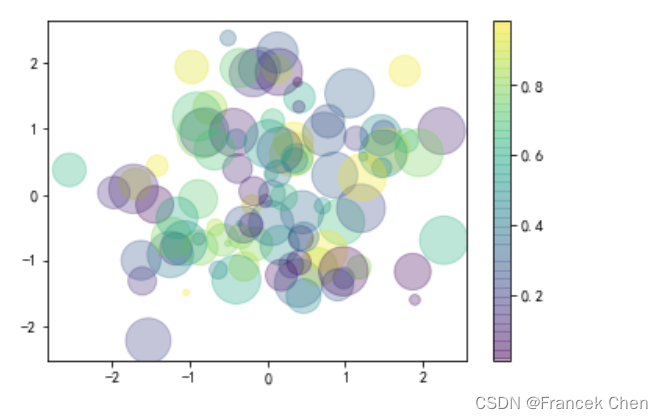
rd = np.random.RandomState(0) # 作用相当于random.seed(),但它返回一个伪随机数生成器对象,可用该对象生成随机数
x = rd.randn(100)
y = rd.randn(100)
colors = rd.rand(100)
sizes = 1000*rd.rand(100)
# 画散点图最重要的5个参数:x-横坐标,y-纵坐标,c-颜色(要求是0~1范围内的浮点值),s-点大小(像素),alpha-透明度
# 当颜色和尺寸使用数组时,常用来表示不同的类别;cmap用来指定颜色的风格,viridis表示翠绿色
plt.scatter(x,y,c=colors,s=sizes,alpha=0.3,cmap='viridis')
plt.colorbar() # 显示颜色条
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
(六)箱线图
使用箱线图,常用于检测与处理异常值。
import pandas as pd
import matplotlib.pyplot as plt
- 1
- 2
数据集meal_order_detail.xlsx下载地址:下载meal_order_detail.xlsx
data = pd.read_excel('meal_order_detail.xlsx')
data.head()
- 1
- 2
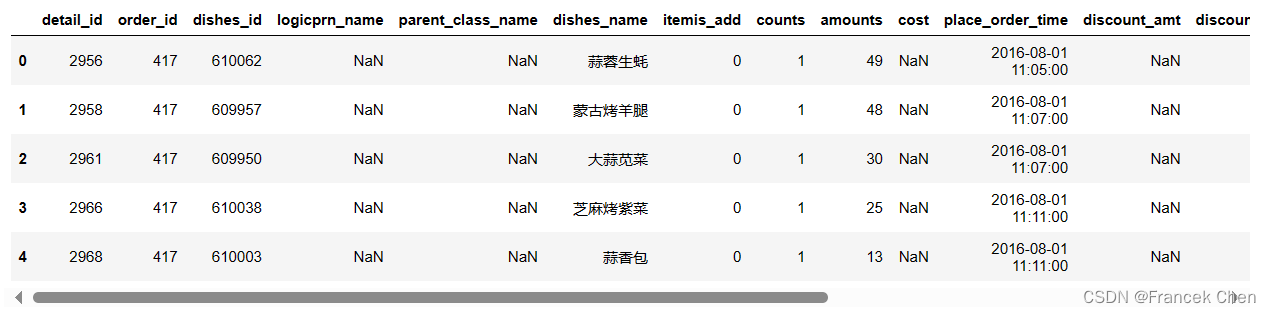
完整数据框如下:
| detail_id | order_id | dishes_id | logicprn_name | parent_class_name | dishes_name | itemis_add | counts | amounts | cost | place_order_time | discount_amt | discount_reason | kick_back | add_inprice | add_info | bar_code | picture_file | emp_id | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2956 | 417 | 610062 | NaN | NaN | 蒜蓉生蚝 | 0 | 1 | 49 | NaN | 2016-08-01 11:05:00 | NaN | NaN | NaN | 0 | NaN | NaN | caipu/104001.jpg | 1442 |
| 1 | 2958 | 417 | 609957 | NaN | NaN | 蒙古烤羊腿 | 0 | 1 | 48 | NaN | 2016-08-01 11:07:00 | NaN | NaN | NaN | 0 | NaN | NaN | caipu/202003.jpg | 1442 |
| 2 | 2961 | 417 | 609950 | NaN | NaN | 大蒜苋菜 | 0 | 1 | 30 | NaN | 2016-08-01 11:07:00 | NaN | NaN | NaN | 0 | NaN | NaN | caipu/303001.jpg | 1442 |
| 3 | 2966 | 417 | 610038 | NaN | NaN | 芝麻烤紫菜 | 0 | 1 | 25 | NaN | 2016-08-01 11:11:00 | NaN | NaN | NaN | 0 | NaN | NaN | caipu/105002.jpg | 1442 |
| 4 | 2968 | 417 | 610003 | NaN | NaN | 蒜香包 | 0 | 1 | 13 | NaN | 2016-08-01 11:11:00 | NaN | NaN | NaN | 0 | NaN | NaN | caipu/503002.jpg | 1442 |
plt.boxplot(data['amounts'])
# plt.boxplot(data['amounts'],vert=False) # vert=False设置水平显示箱形图
plt.show()
- 1
- 2
- 3
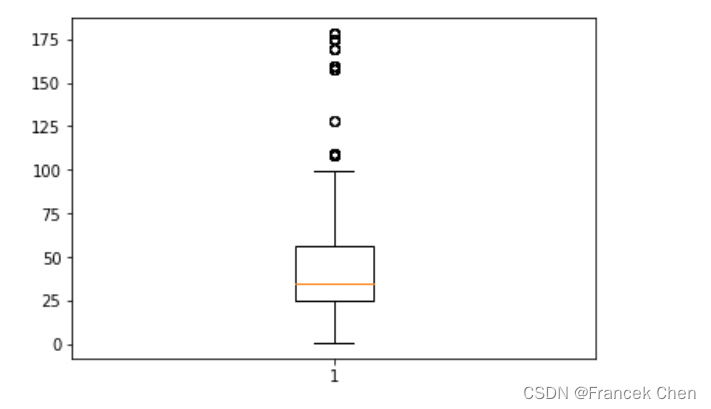
检测与处理异常值
箱型图提供了识别异常值的一个标准,即异常值通常被定义为小于 QL-1.5IQR 或大于 QU+1.5IQR 的值。
- QL称为下四分位数,表示全部观察值中有四分之一的数据取值比它小。
- QU称为上四分位数,表示全部观察值中有四分之一的数据取值比它大。
- IQR称为四分位数间距,是上四分位数QU与下四分位数QL之差,其间包含了全部观察值的一半。
箱线图依据实际数据绘制,真实、直观地表现出了数据分布的本来面貌,且没有对数据做任何限制性要求,其判断异常值的标准以四分位数和四分位数间距为基础。
四分位数给出了数据分布的中心、散布和形状的某种指示,具有一定的鲁棒性,即25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值通常不能对这个标准施加影响。鉴于此,箱线图识别异常值的结果比较客观,因此在识别异常值方面具有一定的优越性。
3 σ 3\sigma 3σ 原则又称为拉依达法则。该法则就是先假设一组检测数据只含有随机误差,对原始数据进行计算处理得到标准差,然后按一定的概率确定一个区间,认为误差超过这个区间的就属于异常值。
这种判别处理方法仅适用于对正态或近似正态分布的样本数据进行处理,如下表所示,其中 σ \sigma σ 代表标准差, μ \mu μ 代表均值, x = μ x=\mu x=μ 为图形的对称轴。数据的数值分布几乎全部集中在区间 ( μ − 3 , μ + 3 ) (\mu-3,\mu+3) (μ−3,μ+3) 内,超出这个范围的数据仅占不到 0.3 % 0.3\% 0.3%。故根据小概率原理,可以认为超出 3 σ 3\sigma 3σ 的部分数据为异常数据。

# 自定义函数用于将数据中的异常值替换为缺失值
def replace(x):
import numpy as np
QU = x.quantile(0.75)
QL = x.quantile(0.25)
IQR = QU -QL
x[(x > (QU + 1.5*IQR)) | (x < (QL - 1.5*IQR))] = np.nan
return x
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
data['amounts'].isnull().sum()
- 1
0
- 1
replace(data['amounts']).isnull().sum()
- 1
C:\Users\Administrator\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame
See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy
import sys
173
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11



