- 1大模型部署手记(15)LLaMa2+Ubuntu18.04+privateGPT_privategpt llama2
- 2final可以用来修饰什么?_final可以修饰哪些
- 3Linux入门学习 —— 常用的基本命令(下)_linux count
- 4解决An HTTP error occurred when trying to retrieve this URL. HTTP errors are often intermittent......_wsus同步报错an http error occurred
- 5Educoder/头歌JAVA——JAVA面向对象:封装、继承和多态_java面向对象封装继承和多态头歌
- 6【2024-04-07】小红书春招笔试三道编程题解(最后一场)_小苯是“小红书app”的一名博主,这天他想要给自己的“铁粉”送一些礼物
- 7arkts鸿蒙沉浸式界面开发api10+_鸿蒙api10
- 8小节测验_统计该系总共有多少名学生,直接打印输出统计的结果。
- 9oracle 64 linux,整理ORACLE官网Linux X86-64系统安装步骤
- 1001-【Jenkins+Mac】-Jenkins安装_jenkins-lts: an unsatisfied requirement failed thi
D-H坐标系与D-H参数——机器人学(二)
赞
踩
D-H坐标系与D-H参数
机器人学(二)
一、D-H参数:
建立坐标系:(一般情况:本轴的坐标系放前后其实都可以(S D-H和M D-H))
连杆编号:将基座记为杆0,从基座往后依次定义杆1,杆2,…,杆i;
任何杆件都可以用两个尺度来表征:公法线长度
a
n
a_n
an和垂直于
a
n
a_n
an平面内轴线之间夹角
α
n
\alpha_n
αn。每根轴线有两个法线,对于每根杆件各有一根。两根杆件距离用
d
n
d_n
dn刻画,夹角用
θ
n
\theta_n
θn描述。
在这里讲解例子把坐标轴放在连杆末端(S D-H法)。对于连杆 i 来说:将连杆 i 的坐标系定在其与连杆 i+1 的连接轴线上, z i z_i zi轴与 i+1 轴方向一致,正向任定,关节 i-1 与 i 的 z z z轴的公垂线作为 x i x_i xi轴,方向由轴 i-1 指向 i 轴,x 轴与 z 轴交点为 O ,右手定则确定轴 y i y_i yi。
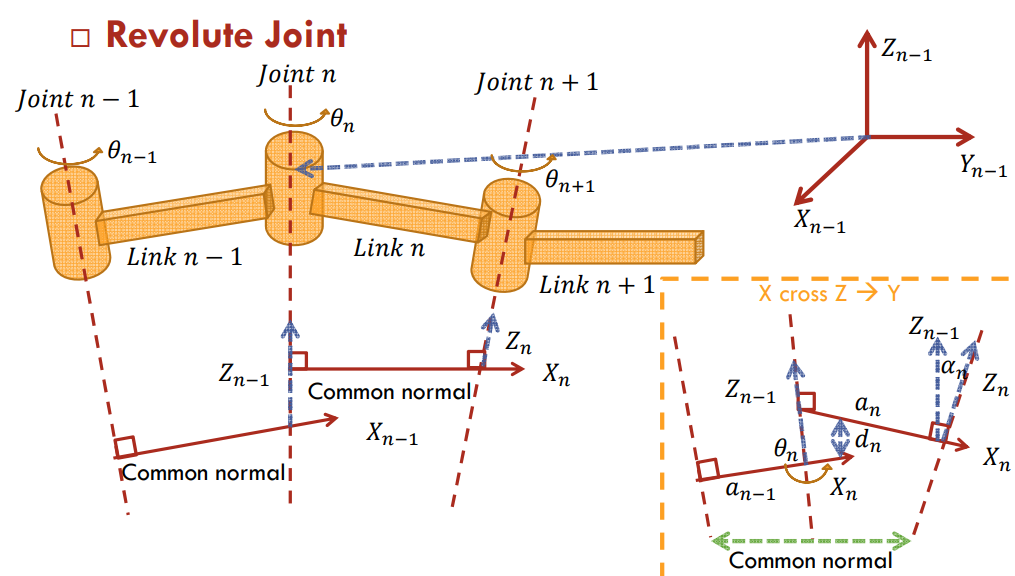
注意:
1
、
1、
1、如果两个关节轴相交,坐标原点定于关节轴的交点。
2
、
2、
2、如果两个关节的z轴平行,那么它们之间就有无数条公垂线。这时可挑选与下一关节的公垂线共线的一条公垂线, 这样做可以简化模型(关节距d为0)。
3
、
3、
3、如果两个相邻关节的z轴是相交的,那么它们之间就没有公垂线(或者说公垂线距离为零)。这时可将垂直于两条轴线构成的平面的直线指定为x轴。也就是说,其公垂线是垂直于包含了两条z轴平面的直线,它也相当于选取两条z轴的叉积方向作为x轴。这样规定也会使模型得以简化。
坐标系变换(从 i-1 轴到 i 轴):
θ i \theta _i θi:关节角,绕 z i − 1 z_{i-1} zi−1旋转,使得 x i − 1 x_{i-1} xi−1与 x i x_{i} xi方向一致;
d i d _i di:偏移位置,延 z i − 1 z_{i-1} zi−1轴,移动距离使得 x i − 1 x_{i-1} xi−1与 x i x_{i} xi共线;
a i a _{i} ai:连杆长度,延 x i − 1 x_{i-1} xi−1移动距离,使原点重合;
α i \alpha _{i} αi:绕 x i x_{i} xi旋转角度,使得 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴重合。
如果中间轴有平移轴:
该轴z方向为关节轴移动方向,则将该坐标轴直接移到下个坐标轴下面,保证当平移轴初始距离为 d i d _i di=0时候为初始时候。
此时没有 a i a _{i} ai,只有 d i d _i di。此时一般将 α i \alpha _{i} αi设为0.
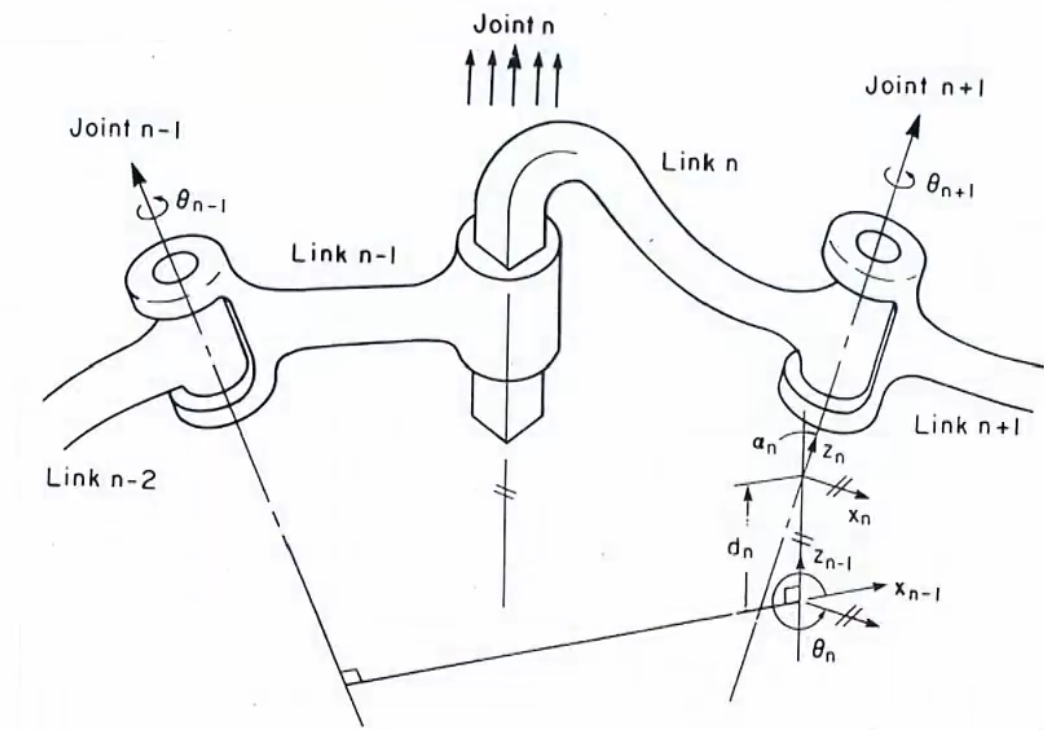
D-H矩阵(四个运动转换形成矩阵): A n A_n An是从系 i-1 到 i 。
\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space
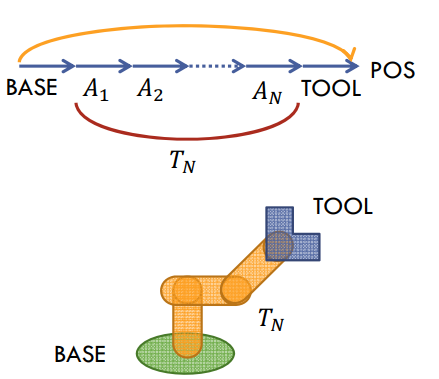 |
\space\space\space\space\space\space
 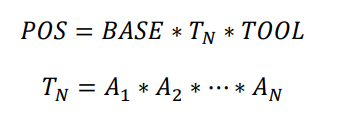 |
|---|
二、:特殊轴
平行轴: d n d _n dn是变量;且初始 d n = 0 d _n=0 dn=0。
旋转轴: θ n \theta _{n} θn是变量;当 x n − 1 x_{n-1} xn−1与 x n x_n xn平行且同向时 θ n = 0 \theta _{n}=0 θn=0。
三、斯坦福机械臂
以此为例写出运动学表格。
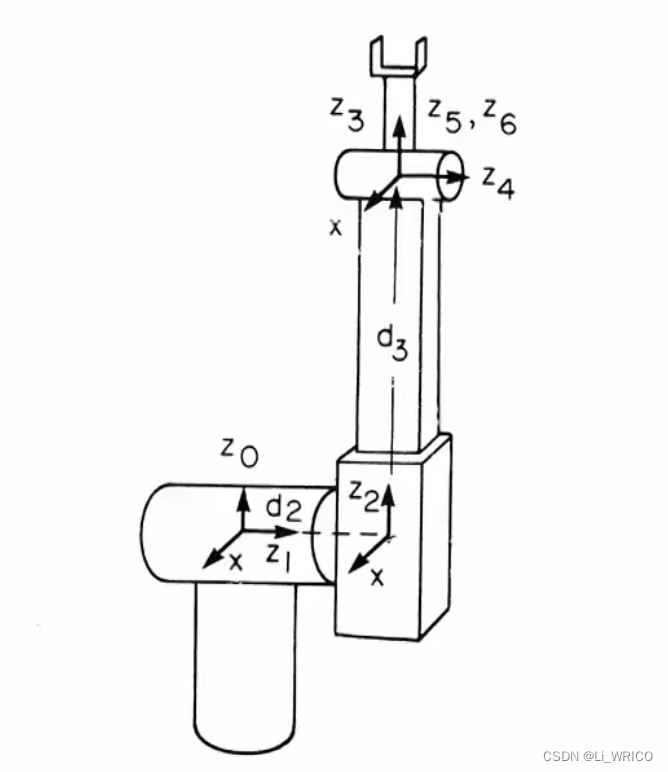
它的运动学表格如下: