灰狼优化算法GWO求解置换流水车间调度问题FSP_pfsp

灰狼优化算法GWO求解置换流水车间调度问题

置换流水车间调度问题（PFSP）是一类最基本、最经典的流水车间调度问题，本文主要讨论使用灰狼优化算法（GWO）求解单目标PFSP。

置换流水车间调度问题模型

一般的置换流水车间调度问题可以被描述为：一组 n 个工件通过一组 m 台机器以相同的顺序进行处理。每个工件 i 在不同的机器上有一系列相应的操作 j，这些操作的处理时间是确定的，用以下符号表示：O_i1，O_i2，…，O_ij，…，O_im。这些工件在车间内必须要遵循的规则是每个工件在所有机器上的加工顺序都是相同的，并且每台机器都必须以相同的顺序处理所有的工件，最终的目标是找到最大完工时间最小（或者其他优化目标）的工件序列。

一般，置换流水车间调度问题主要的假设和约束条件总结如下：
（1）所有工件都没有优先级约束。
（2）每个工件一次仅在一台机器上处理，每台机器一次只能处理一个工件。
（3）工件数量及其在每台机器上的执行时间是已知的、确定的并且是独立的。
（4）执行时间包括设置时间、处理时间和运输时间。
（5）一旦开始在机器上处理工件，此过程在完成之前不能中断。
（6）每台机器都以相同的顺序处理工件。

一个简单的PFSP甘特图如下：

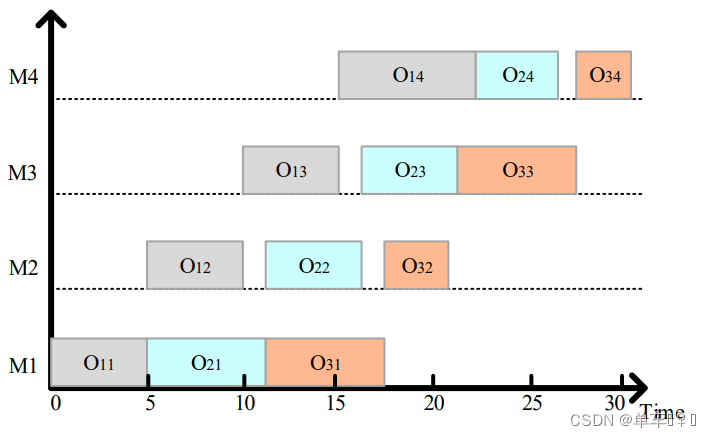
置换流水车间的数学模型

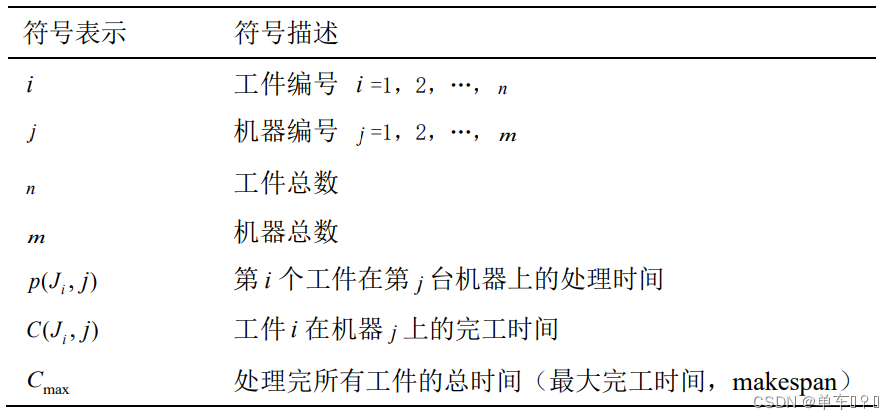
置换流水车间调度问题的数学模型建立如下：对于 m 台机器和 n 个工件，最大完工时间 Cmax 可以通过以下公式计算：

灰狼优化算法

灰狼优化算法(Grey Wolf Optimization, GWO)由 Seyedali、Seyed 和 Lewis于 2014 年提出的一种群体智能优化算法，它的提出基于对灰狼群体觅食行为及等级制度的观察后建模所得。在函数优化问题中相比较粒子群算法、遗传算法它的收敛速度快、精度高，也由于它控制参数少、易实现的特点，使它广泛应用于多个工程领域，近年来已成为群体智能优化算法领域的研究热点。

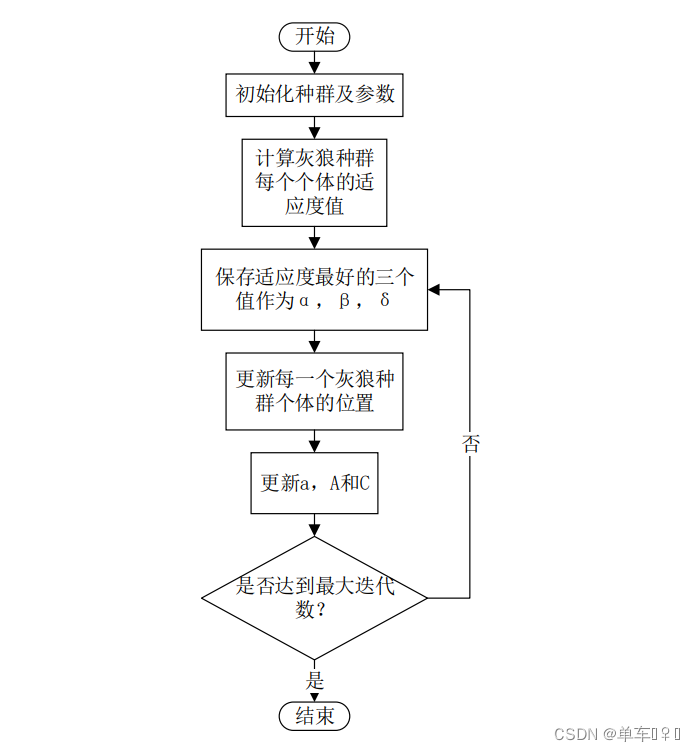
本文采用GWO算法对置换流水车间问题进行求解，本文以一个随机算例进行测试，算例规模为 10x6 ，即10个工件，6台机器（等于阶段数）。

算例的Excel数据如下：

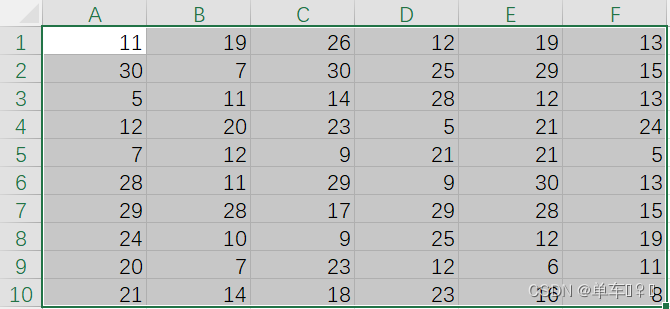
GWO程序的部分代码如下：

main.m

```
clear all; clc

%% 数据生成
data_read();
load jobinfo.mat            % jobinfo.mat 通过 data_read.m文件产生
disp(['工件数', num2str(jobNum), '  机器数', num2str(machineNum)]);
disp('数据加载成功');

%% 灰狼优化器
% machineNum：       机器数量
% jobNum：           工件数量
% jobInfo：          加工时间信息
% Alpha_score：      α狼--最优目标函数值
% Alpha_pos：        α狼--最优解
% Convergence_curve：迭代曲线
% machine_table：    包含每台机器任意时刻的加工信息（开始时间，结束时间，工件号，机器号）
cd('GWO\')
[Alpha_score, Alpha_pos, Convergence_curve, machine_table] = GWO(machineNum, jobNum, jobInfo);
cd('..\')

%% 画出迭代曲线
figure(1);
plot(Convergence_curve.min, 'r-', 'LineWidth', 1.5);
hold on
plot(Convergence_curve.avg, 'b-.', 'LineWidth', 1.5);
box on; grid on
legend('最小值', '平均值')
title('迭代曲线');
xlabel('迭代次数');
ylabel('最大完工时间');

%% 画出Gantte图
figure(2)
gantt_chart(machine_table);
xlabel('时间');
ylabel('机器编号');
```
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

GWO.m

%% GWO灰狼算法
function [Alpha_score, Alpha_pos, Convergence_curve, machine_table] = GWO(machineNum, jobNum, jobInfo)

%% 算法参数：种群数量，迭代次数
wolf_num = 100;     % 种群规模
max_iter = 100;     % 最大迭代次数

%% 初始化alpha，beta，delta狼，维度：2 * sum(operaVec)
dim = jobNum;               % 自变量维度
Alpha_pos = zeros(1, dim);  % 初始化α狼
Alpha_score = inf;
Beta_pos = zeros(1, dim);   % 初始化β狼
Beta_score = inf;
Delta_pos = zeros(1, dim);  % 初始化δ狼
Delta_score = inf;
LB = -jobNum * ones(1, dim);    % 自变量下界
UB = jobNum * ones(1, dim);     % 自变量上界

%% 初始化种群
wolf = rand(wolf_num, dim) * 2 * jobNum - jobNum;   % 随机生成种群 [-jobNum, jobNum]

%% 主循环
Convergence_curve_min = zeros(1, max_iter);     % 迭代曲线：最小值
Convergence_curve_avg = zeros(1, max_iter);     % 迭代曲线：均值
iter = 0;
while iter < max_iter
    c_max_rem = zeros(1, max_iter);     % 临时记录种群目标函数值

    for i = 1: size(wolf, 1)

        % 超界数值进行规整
        wolf(i, :) = bound(wolf(i, :), UB, LB);

        % 计算目标函数值
        makespan = fitness(wolf(i, :), machineNum, jobNum, jobInfo);
        c_max_rem(i) = makespan;

        % 更新alpha，beta，delta狼
        if makespan < Alpha_score 
            Alpha_score = makespan; % Update alpha
            Alpha_pos = wolf(i, :);
        end
        if makespan > Alpha_score && makespan < Beta_score 
            Beta_score = makespan; % Update beta
            Beta_pos = wolf(i, :);
        end
        if makespan > Alpha_score && makespan > Beta_score && makespan < Delta_score 
            Delta_score = makespan; % Update delta
            Delta_pos = wolf(i, :);
        end
    end

    % 非线性a值：从2降到0
    a = 2 - iter * (2 / max_iter);
    
    % 更新狼群
    for i = 1: size(wolf, 1)
        for j = 1: size(wolf, 2)                 
            r1 = rand;  % r1 is a random number in [0,1]
            r2 = rand;  % r2 is a random number in [0,1]
            
            A1 = 2 * a * r1 - a;    % Equation (3.3)
            C1 = 2 * r2;            % Equation (3.4)
            
            D_alpha = abs(C1 * Alpha_pos(j) - wolf(i, j));      % Equation (3.5)-part 1
            X1 = Alpha_pos(j) - A1 * D_alpha;                   % Equation (3.6)-part 1
                       
            r1 = rand;
            r2 = rand;
            
            A2 = 2 * a * r1 - a;    % Equation (3.3)
            C2 = 2 * r2;            % Equation (3.4)
            
            D_beta = abs(C2 * Beta_pos(j) - wolf(i, j));        % Equation (3.5)-part 2
            X2 = Beta_pos(j) - A2 * D_beta;                     % Equation (3.6)-part 2       
            
            r1 = rand;
            r2 = rand; 
            
            A3 = 2 * a * r1 - a;    % Equation (3.3)
            C3 = 2 * r2;            % Equation (3.4)
            
            D_delta = abs(C3 * Delta_pos(j) - wolf(i, j));      % Equation (3.5)-part 3
            X3 = Delta_pos(j) - A3 * D_delta;                   % Equation (3.5)-part 3             
            
            wolf(i, j) = (X1 + X2 + X3) / 3;        % Equation (3.7)
        end
    end

    %% disp
    disp(['Cur gen：', num2str(iter),' ||makespan(Alpha_score)：', num2str(Alpha_score)]);
    iter = iter + 1;    
    Convergence_curve_min(iter) = Alpha_score;
    Convergence_curve_avg(iter) = mean(c_max_rem);
end

Convergence_curve.min = Convergence_curve_min;
Convergence_curve.avg = Convergence_curve_avg;
% machine_table 包含每台机器任意时刻的加工信息（开始时间，结束时间，工件号，机器号）
[~, machine_table] = fitness(Alpha_pos, machineNum, jobNum, jobInfo);
end

%% bound function
function a = bound(a, ub, lb)
a(a > ub) = ub(a > ub);
a(a < lb) = lb(a < lb);
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107

GWO算法的求解结果如下：

GWO的迭代曲线如下：

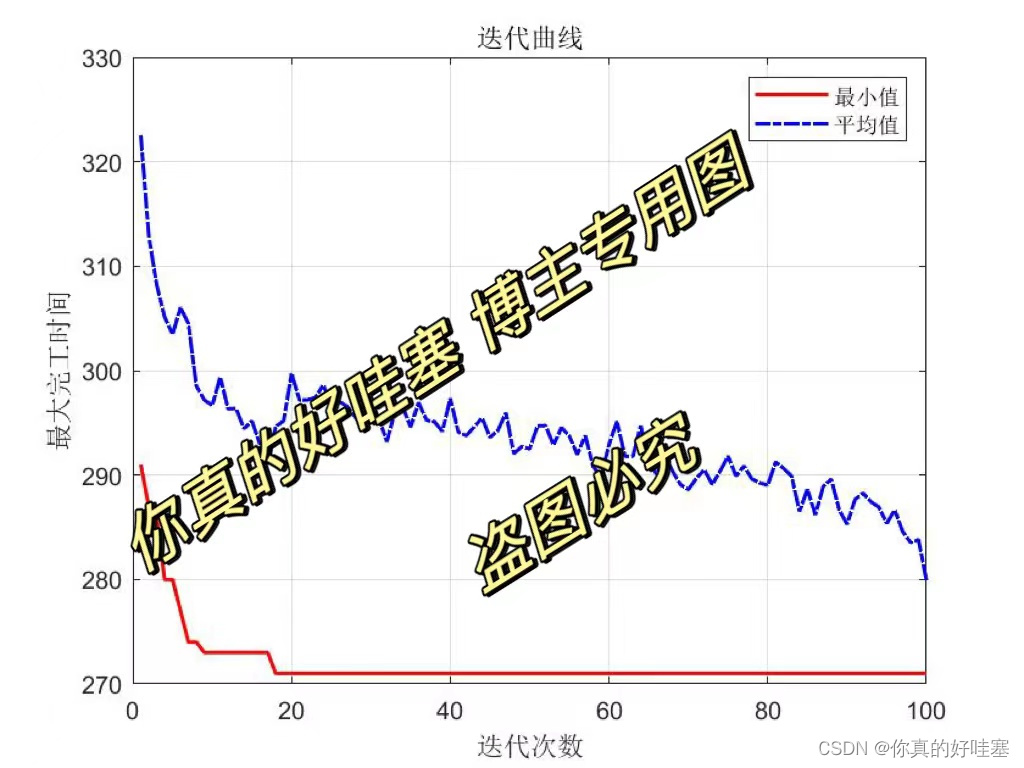
GWO求解的算例甘特图如下：

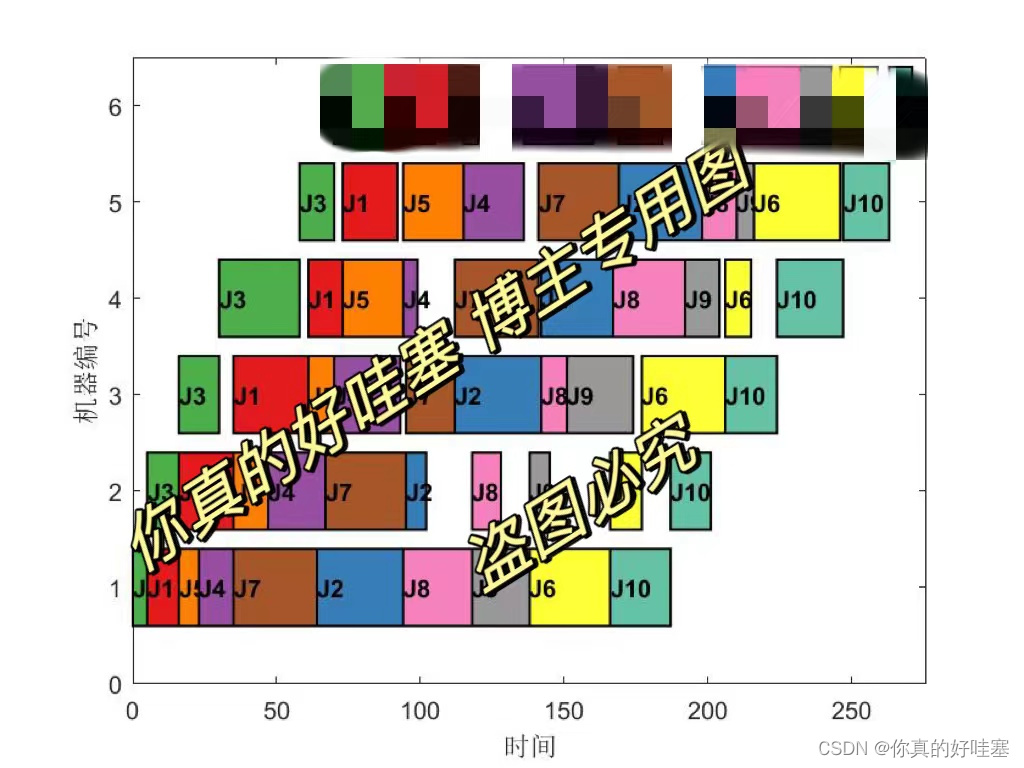
权利声明：

未经本人允许，本文所有内容禁止搬运，严禁盗图盗文！

代码传送门

本文代码及各种车间调度问题可咨询：
（1）扣扣：3249992049
（2）私信咨询 ~~