【数据结构】时间复杂度与空间复杂度_时间复杂度曲线图

前言

在学习C语言的时候，大多数的小伙伴们并不会对算法的效率了解，也许算法也是一个陌生的领域，当进入了数据结构这个模块，就应该对算法的效率做一个清晰的认识。但是算法的效率是什么呢？这里就引出来时间复杂度与空间复杂度的概念了。

一、算法效率

1. 算法效率的定义

算法效率指的是算法解决问题所需的时间和空间资源。通常用时间复杂度和空间复杂度来衡量一个算法的效率。
对于初学者来说，这里看到复杂度会被认为是代码的的多少，但是这是错误的。

---

这里举个例子：(这里递归函数看着代码很少，但是这里的时间复杂度很大）

int Fac(int n)
{
	if (n <= 2)
		return Fac(n - 1) + Fac(n - 2);
	else
		return 1;
}
1
2
3
4
5
6
7

二、时间复杂度

1. 时间复杂度的定义

时间复杂度是算法在执行时所需的时间资源与问题规模之间的关系。通常以最坏情况下的运行时间为衡量标准，用大O符号来表示。

2. 时间复杂度的计算

计算时间复杂度可以通过分析算法中基本操作的执行次数来完成，然后根据这些操作次数的增长趋势得出算法的时间复杂度。
计算时间复杂度的原则是：根据算法中基本操作重复执行的次数来估算算法的时间复杂度，忽略常数项和低阶项，保留最高阶项。

推导大O阶方法:
1、若执行次数都是常数，则用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，常数和低阶项全部去除，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

三、空间复杂度

1. 空间复杂度的定义

空间复杂度是算法在执行时所需的内存资源与问题规模之间的关系。同样以最坏情况下所需的额外空间为衡量标准，使用大O符号表示。

2. 空间复杂度的计算

计算空间复杂度可以通过分析算法中使用的临时变量、数据结构等占用的空间大小来完成，然后根据这些空间大小的增长趋势得出算法的空间复杂度。
计算空间复杂度的原则是：根据算法中所需存储空间的大小来估算算法的空间复杂度，–忽略常数项和低阶项，保留最高阶项。

推导大O阶方法:
1、若运行时间都是常数，则用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，常数和低阶项全部去除，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

四、时间复杂度曲线图

这是在电脑计算机中绘画出的图，或许有人觉得这些曲线会差不多，但是当我将这个图片缩小后就会发现区别了。

---

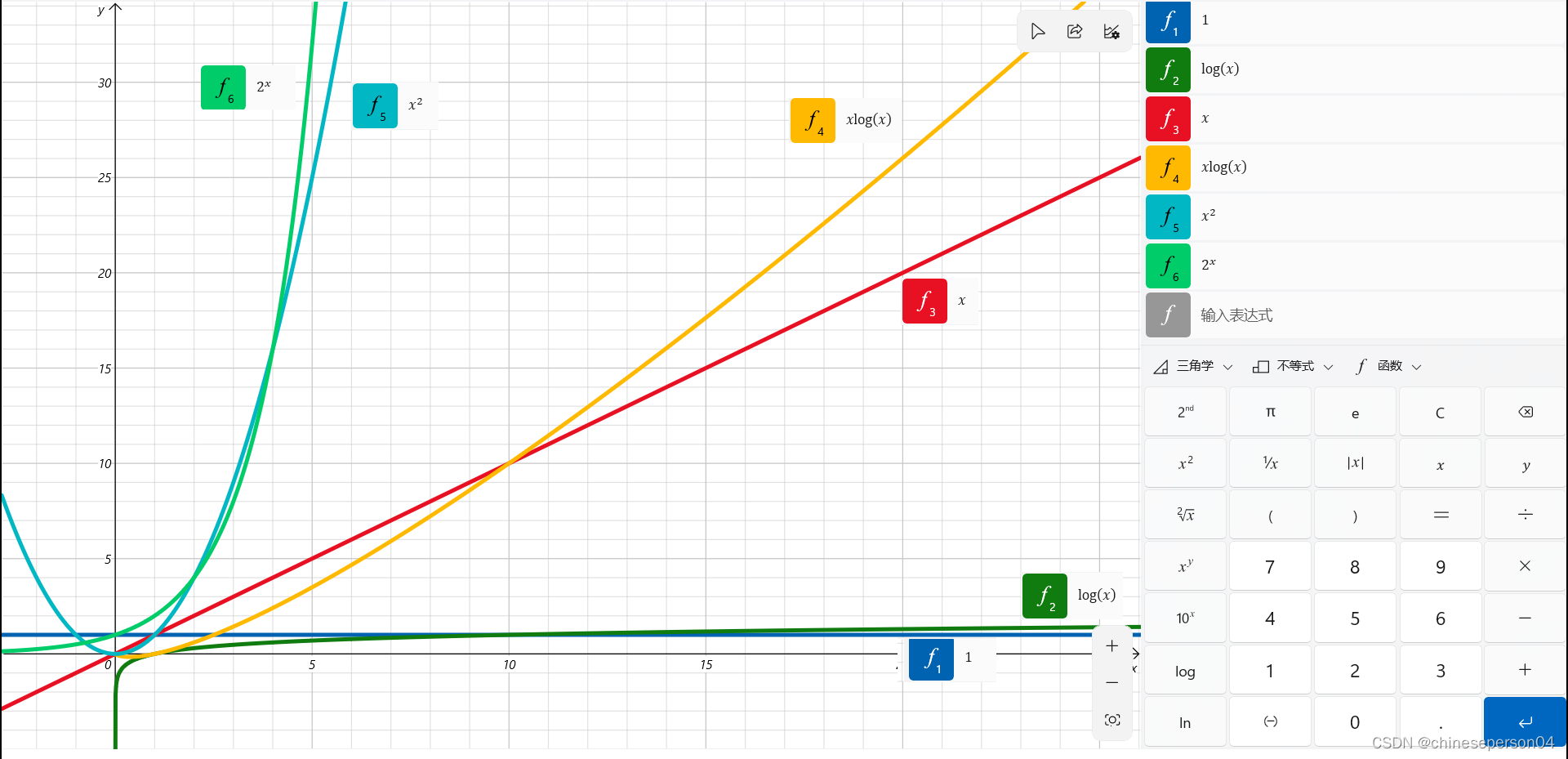
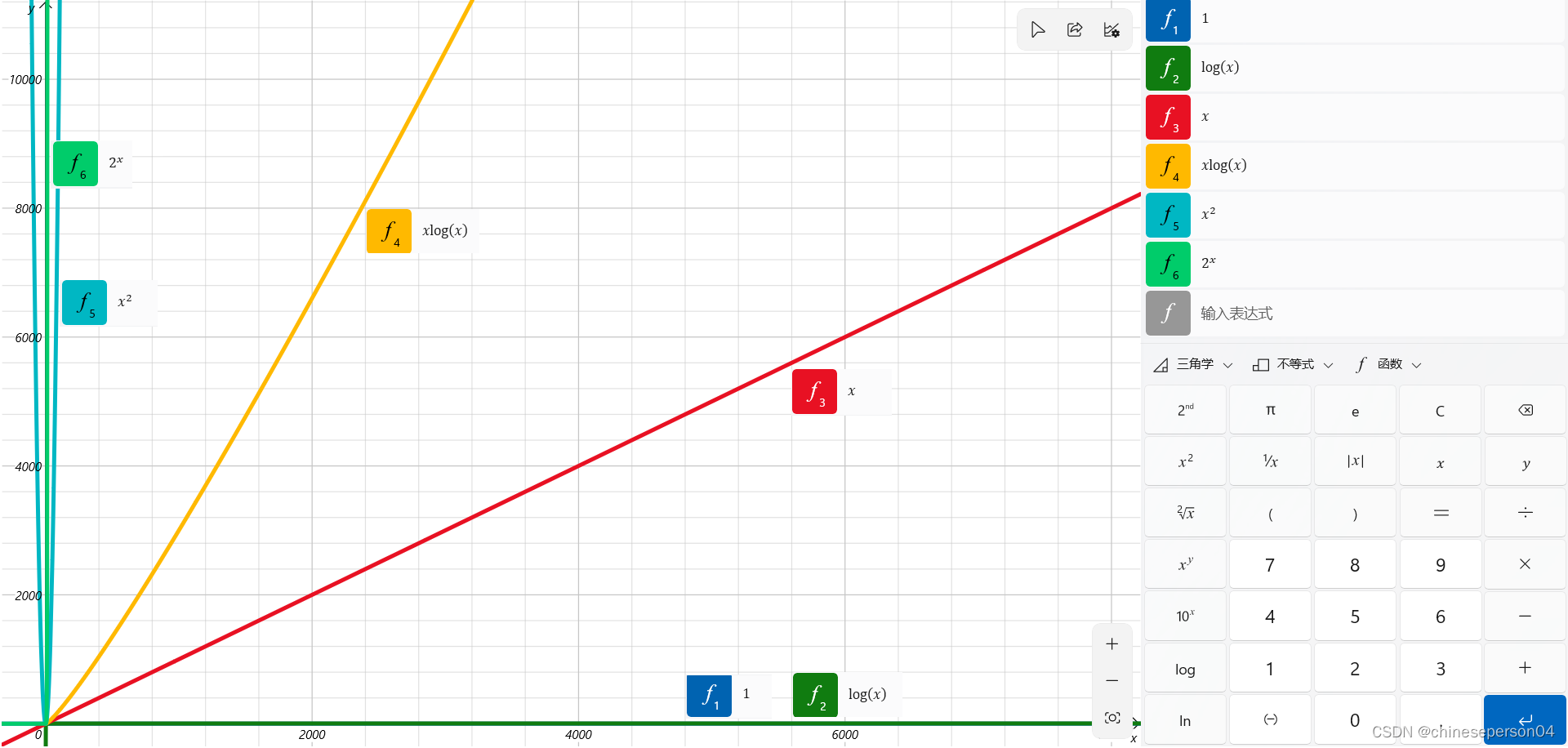
这里缩小后发现三个相对分区：（这里用时间复杂度表示）

1. 无限接近于 y轴 ：二次方以上的幂函数( O (n ^ 2) )和大于一为底的指数函数
   (O(n ^ k))，这里还包括一个阶乘(O(n!))（由于增长速度太快，电脑上绘画不出来,图片上就将其省略）。
2. x轴 与 y轴 之间：一次函数 (O(n)) 和 线性对数 ( O(n * log(n)) ）
3. 无线接近与 x轴：常数( O(1)) 和 对数 ( O(log(n)))

结论：
上述三种中，若时间复杂度为第二条，那么这个程序只能算一般。尽量不要写出第一种，在实际开发中几乎不会使用这样时间复杂度的程序，因为太难维护。相比之下第三种写出来的程序是最好的。

结尾

如果有什么建议和疑问，或是有什么错误，大家可以在评论区中提出。
希望大家以后也能和我一起进步！！