数据结构——二叉树的实现

一、二叉树概念的回顾

一棵二叉树是结点的一个有限集合，该集合:

1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

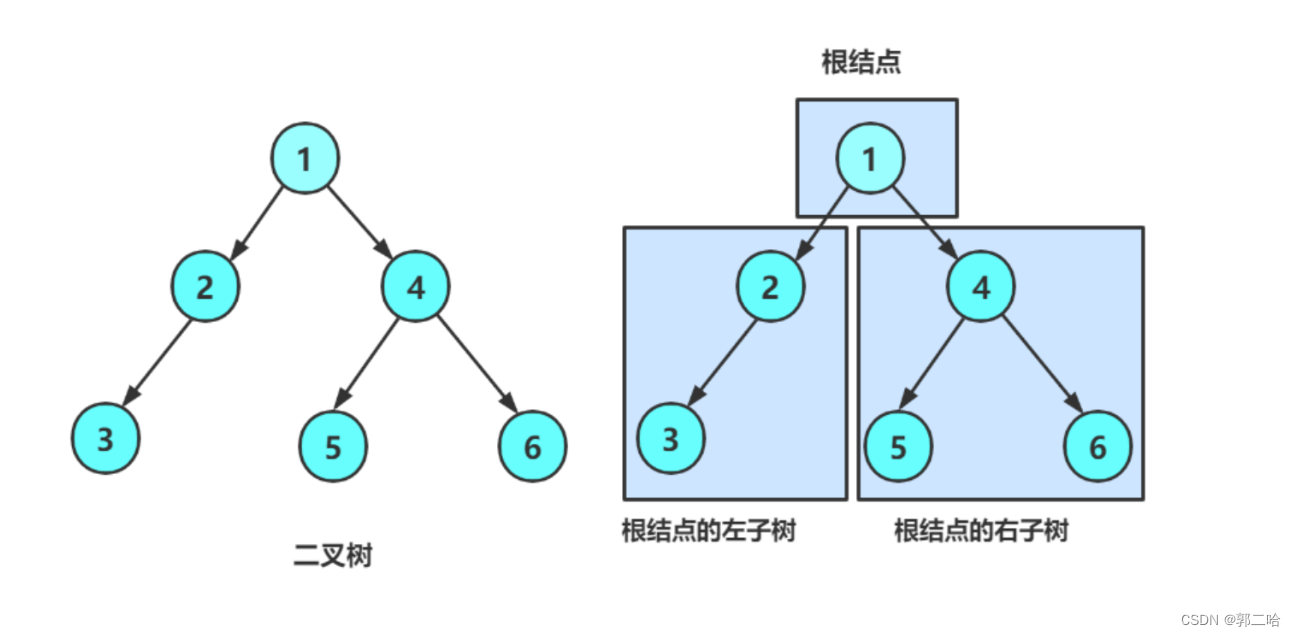
注意：
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的

二、二叉树结构的定义

前面我们提到了二叉树的结构既可以用二叉链也可以用三叉链，下面我们基于二叉链来实现二叉树

//定义二叉树结构
typedef int BTDataType;
typedef struct BinaryTree
{
	BTDataType val;//储存数据
	struct BinaryTree* left;//左孩子结点
	struct BinaryTree* right;//右孩子结点
}BTNode;
1
2
3
4
5
6
7
8

三、二叉树的创建

方法一、写个创建结点的函数然后手动链接起来

创建结点的函数

//创建结点
BTNode* BuyNode(BTDataType x)
{
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("malloc fail");
		exit(1);
	}
	root->val = x;
	root->left = NULL;
	root->right = NULL;
	return root;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

手动链接

//手动创建一个二叉树
BTNode* CreateNode()
{
	BTNode* n1 = BuyNode(1);
	BTNode* n2 = BuyNode(2);
	BTNode* n3 = BuyNode(3);
	BTNode* n4 = BuyNode(4);
	BTNode* n5 = BuyNode(5);
	BTNode* n6 = BuyNode(6);
	//BTNode* n7 = BuyNode(6);

	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	//n2->right = n7;
	n4->left = n5;
	n4->right = n6;

	return n1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

这样我们就成功创建了一个二叉树，如图

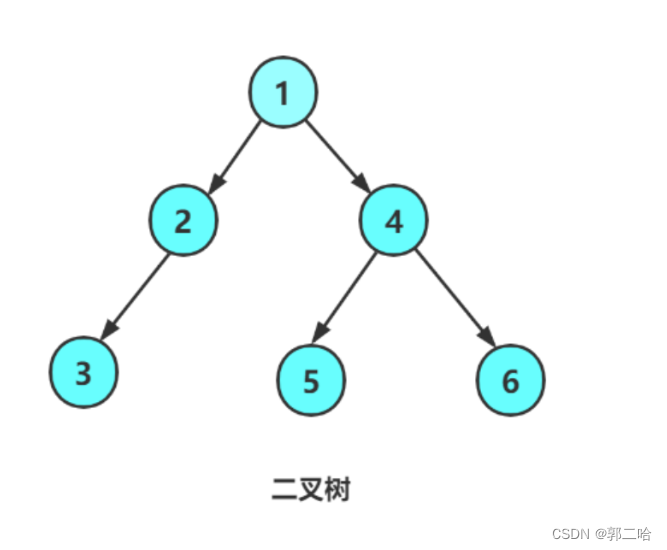
方法二、通过前序遍历的数组的方式构建二叉树

这里我们先来了解一下二叉树的遍历
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

例如在下面的数组的基础上利用前序遍历的思想创建二叉树

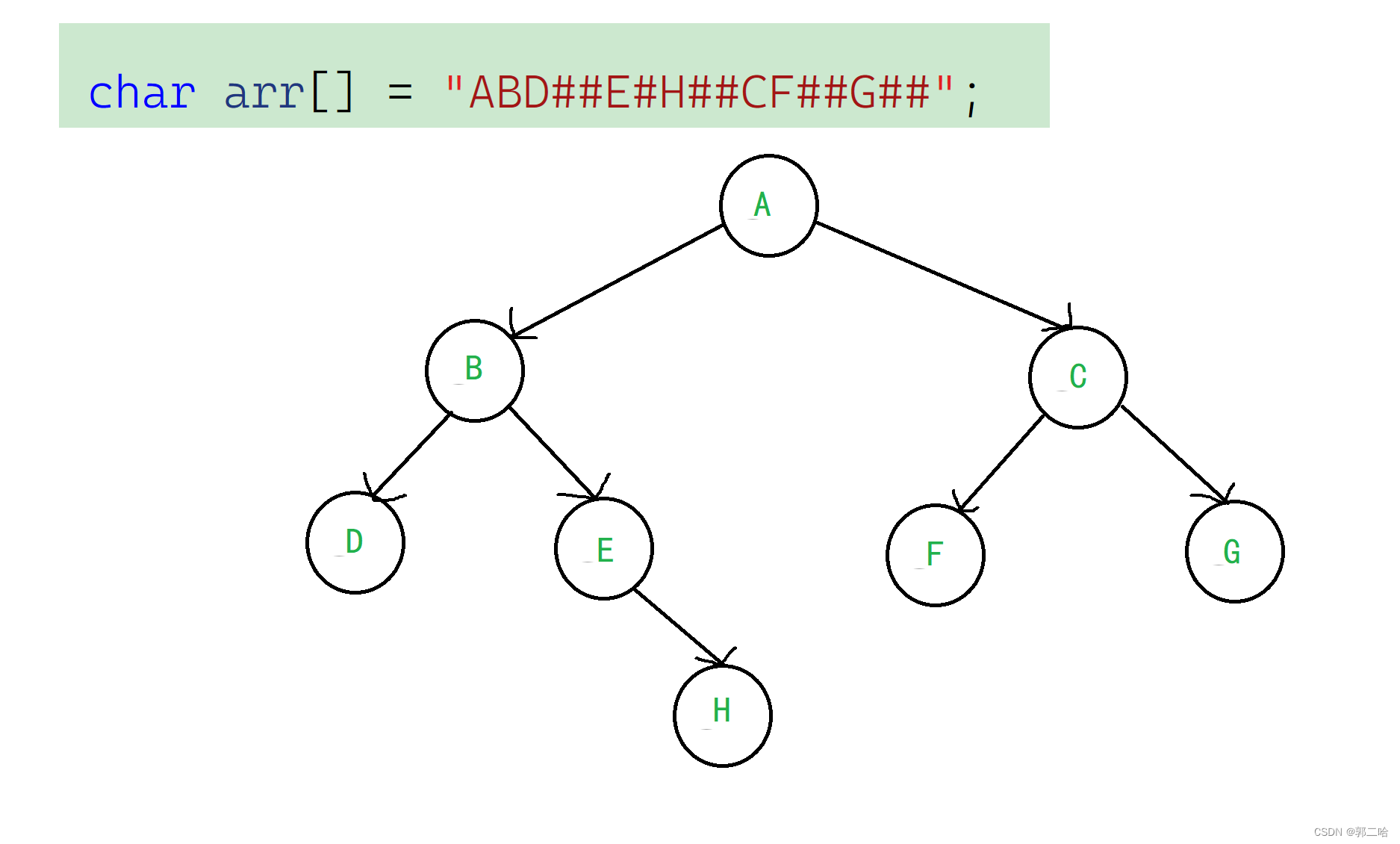
创建的函数声明

BTNode* BTCreateNode(BTDataType* a,int n,int* pi);
1

1.根据前序遍历的思想，我们发现数组的首元素就是根，通过递归本函数，我们可以先将根创建完后再创建左子树，然后创建右子树

2.遇到 # 就将此位置置为空指针然后退出递归，回到上一级

3.创建二叉树的其实就是一个堆逻辑的数组，为了改变下标，我们需要一个能够在递归时确定当前元素下标的变量，因此我们可以传地址，这样即使在递归途中，元素的下标就可以不断改变

创建函数的定义

BTNode* BTCreateNode(BTDataType* a,int n,int* pi)
{
	
	if ((*pi) >= n || a[(*pi)] == '#')
	{
		(*pi)++;//不能在外面++，因为如果不是"#"，就不能跳过此位置
		return NULL;
	}
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(1);
	}
	node->val = a[(*pi)++];
	node->left = BTCreateNode(a, n, pi);
	node->right = BTCreateNode(a, n, pi);
	return node;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

四、 二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。
所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。

遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right
subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

注意：前序遍历、中序遍历、后序遍历普遍用的是递归的思想

前序遍历

前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

其实访问顺序就是根 -> 左 ->右

下面画下前序遍历的递归过程

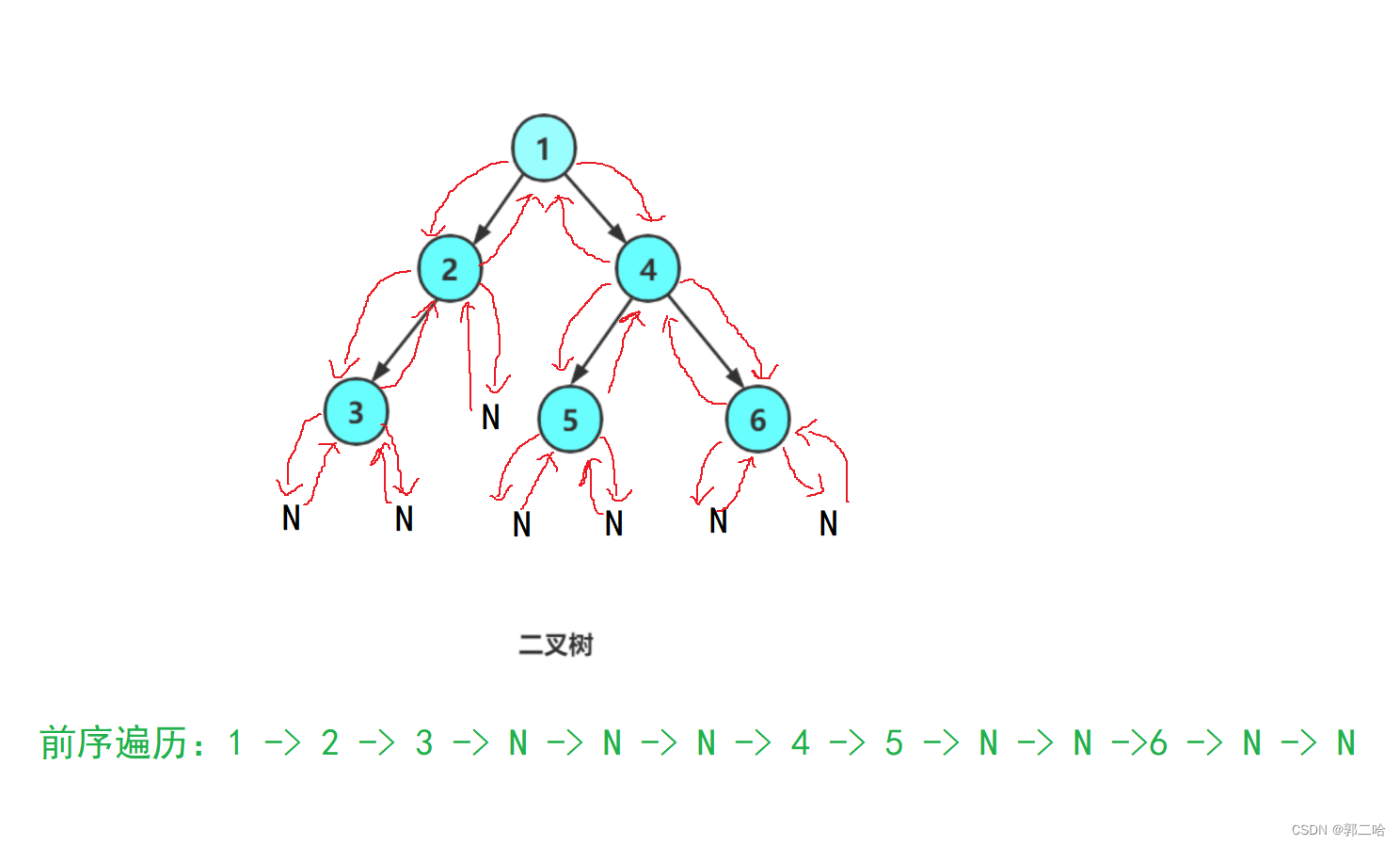
代码实现

//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12

中序遍历

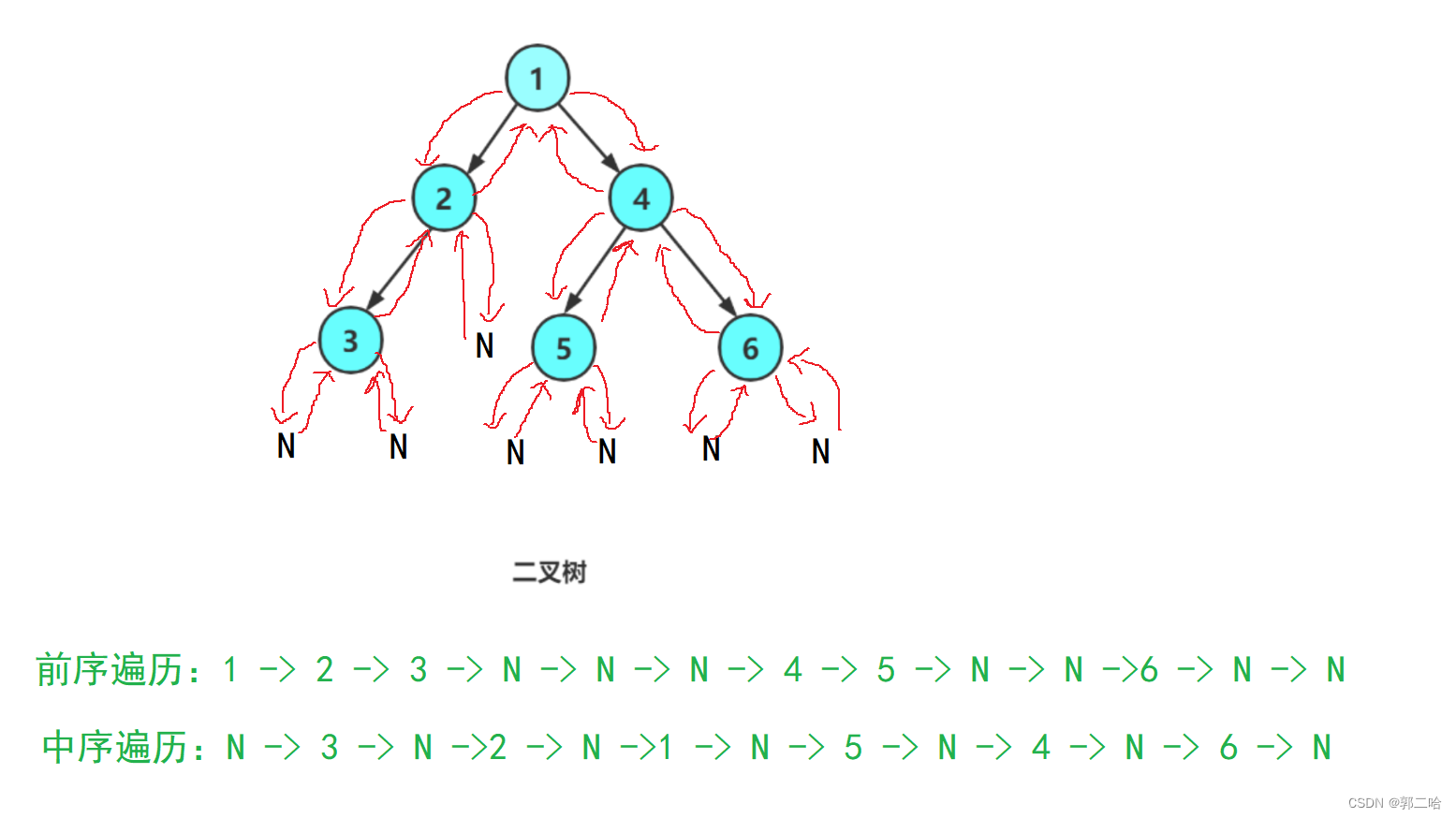
中序遍历(Inorder Traversal) ——访问根结点的操作发生在遍历其左右子树之中（间）。
其实访问顺序就是左 -> 根 ->右

与前序遍历的思想差不多，就是访问顺序改变了一下

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->val);
	InOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12

后序遍历

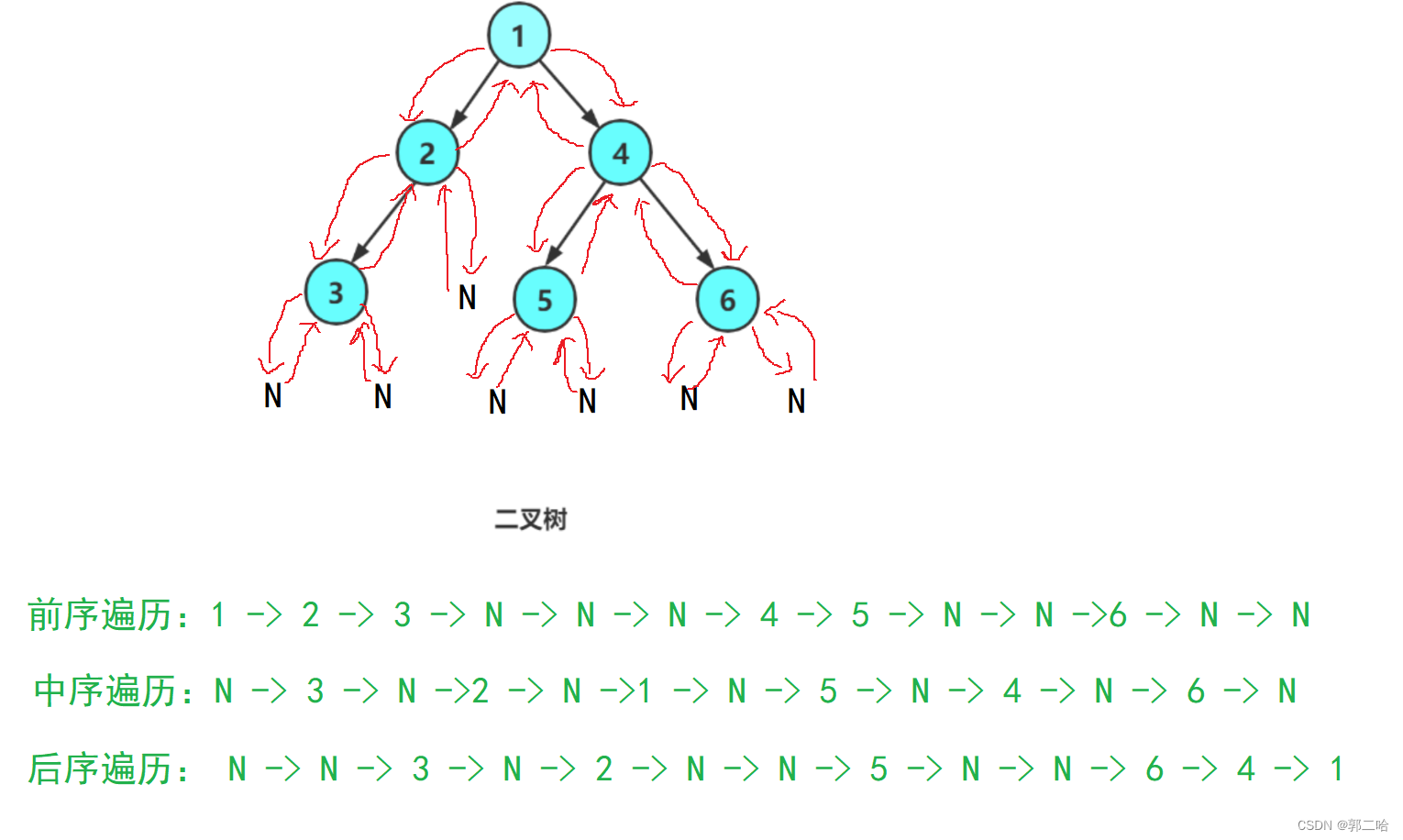
后序遍历(Postorder Traversal) ——访问根结点的操作发生在遍历其左右子树之后。
其实访问顺序就是左 -> 右 ->根
与前序遍历的思想类似，改变访问顺序即可

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);
}

1
2
3
4
5
6
7
8
9
10
11
12
13

层序遍历

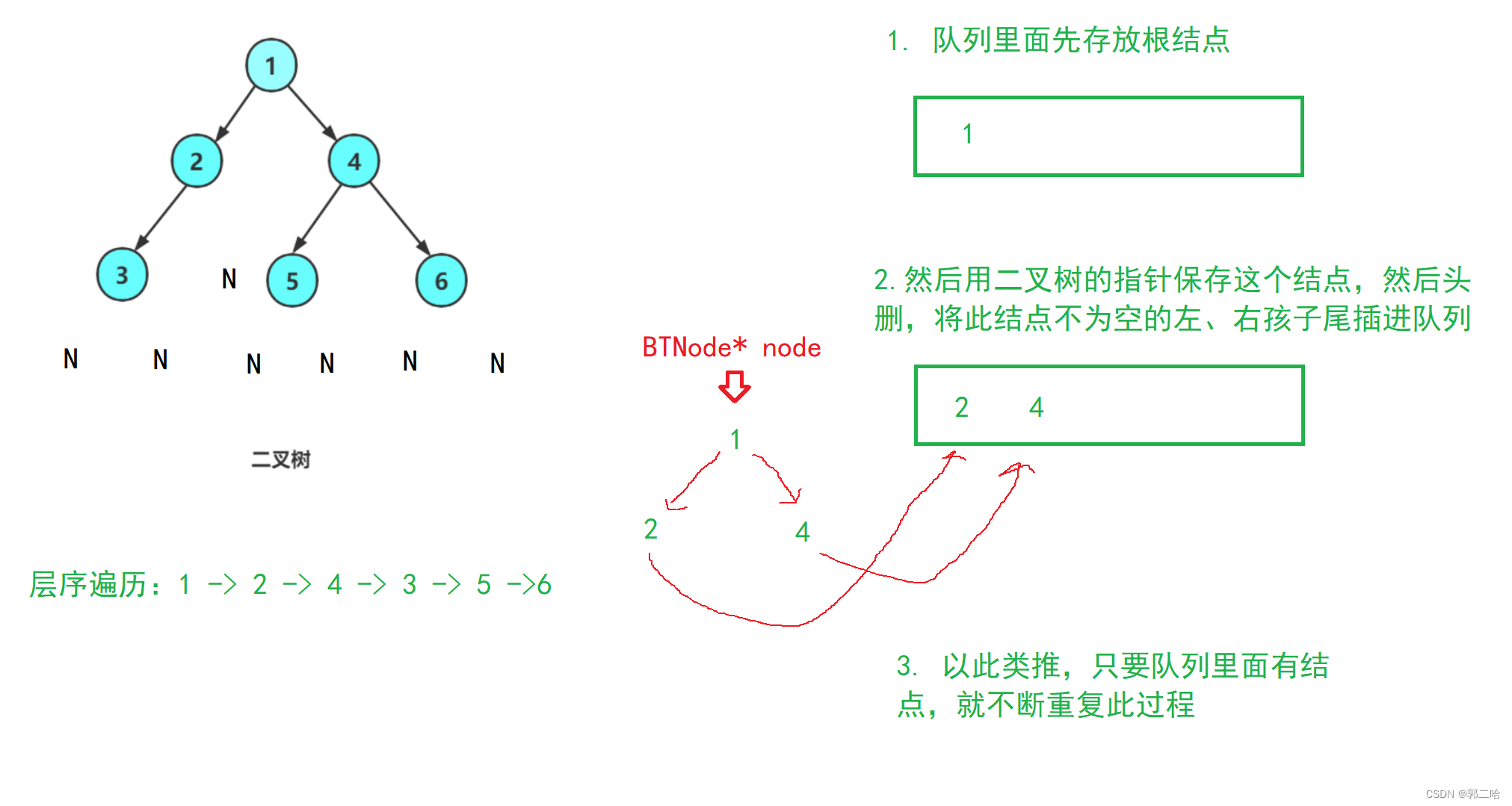
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。 设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发， 首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历

层序遍历可以借助队列的结构来实现

//层序遍历 -> 借助队列
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* node = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", node->val);
		if (node->left)
		{
			QueuePush(&q, node->left);
		}
		if (node->right)
		{
			QueuePush(&q, node->right);
		}
	}
	QueueDestroy(&q);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

五、二叉树的其他功能

二叉树的销毁

首先我们容易想到从根结点开始以次销毁，但是如果先将根结点销毁，那么就找不到左、右孩子了， 故我们可以反过来想， 先销毁左、右孩子，然后再销毁根结点

//二叉树的销毁
void BTDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	//利用后序遍历的思想销毁二叉树
	BTDestroy(root->left);
	BTDestroy(root->right);
	free(root);
}
1
2
3
4
5
6
7
8
9
10
11
12

树的结点个数

采用递归的思想，有结点就去访问左、右孩子，没有结点就返回0

//树的结点个数
int BTSize(BTNode* root)
{
	return root == NULL ? 0 : BTSize(root->left) + BTSize(root->right) + 1;
}
1
2
3
4
5

树的叶子结点个数

在寻找树的结点个数的前提下，加个判断，只要左、右孩子同时为空，才能返回 1

//树的叶子结点个数
int BTLeaveSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BTLeaveSize(root->left) + BTLeaveSize(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

第K层结点的个数

容易想到第一层的结点个数为1个，第二层的结点个数是第一层的左、右孩子不为空的个数，以此类推，第K层结点个数是第K - 1 层的孩子结点存在个数

//第K层结点的个数
int BTKSize(BTNode* root,int k)
{
	if (root == 0)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BTKSize(root->left, k - 1) + BTKSize(root->right, k - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

树的高度

树的高度就是该树的深度，即左、右孩子之中的深度最大的那一个
注意： 应该将左、右孩子的深度给保存，减少递归的次数

//树的高度
int BTHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	int leftHeight = BTHeight(root->left);
	int rightHeight = BTHeight(root->right);
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

查找值为k的结点

根结点找到就返回，否则在左、右孩子之间查找
注意： 如果在左孩子里面找到了，就可以直接返回了，没有必要再在右孩子里面查找

//查找值为K的结点
BTNode* BTFind(BTNode* root, BTDataType k)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->val == k)
	{
		return root;
	}
	BTNode* leftFind = BTFind(root->left, k);
	if (leftFind)
	{
		return leftFind;
	}
	BTNode* rightFind = BTFind(root->right, k);
	if (rightFind)
	{
		return rightFind;
	}
	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

判断是否是完全二叉树

其实就是在层序遍历的基础上，不管左、右孩子是不是为空，直接插入到队列里面

如果遇见第一个非空，就跳出循环，遍历此时的队列里面是否还有非空结点，没有就是完全二叉树，有就不是完全二叉树

//判断是否是完全二叉树
int CompleteTree(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* node = QueueFront(&q);
		QueuePop(&q);
		if (node == NULL)
		{
			break;
		}
		QueuePush(&q, node->left);
		QueuePush(&q, node->right);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* node = QueueFront(&q);
		QueuePop(&q);
		if (node)
		{
			QueueDestroy(&q);
			return 0;
		}
	}
	QueueDestroy(&q);
	return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33