- 1Github Copilot 的使用方法和快捷键_github copilot使用
- 2webpack手动搭建vue项目(七)—— 单元测试覆盖率_babel7使用babel-plugin-istanbul
- 3【前端】使用window.print() 前端实现网页打印详细教程(含代码示例)
- 4vxe-table 和 vxe-grid 的区别,有什么区别_vxe-table vxe-grid
- 5语言模型(二) 评估和类别_语言模型不确定性度量
- 6NetworkManager前世今生:探索网络管理的奥秘与发展趋势_networkmanager被淘汰
- 7基于微信小程序的酒店管理系统 毕业论文+任务书+选题表+开题报告+答辩PPT+项目前后台源码及数据库文件_小程序毕设答辩ppt
- 8php登录后怎么退出来,php登录后点击退出登录的方法
- 9非关系型数据库NoSQL数据层解决方案 之 redis springboot整合与读写操作 2024详解以及window版redis5.0.14下载百度网盘
- 10一款简单、好用的跨平台WEB前端开发框架_跨平台web框架
详解人工智能之确定性推理方法
赞
踩
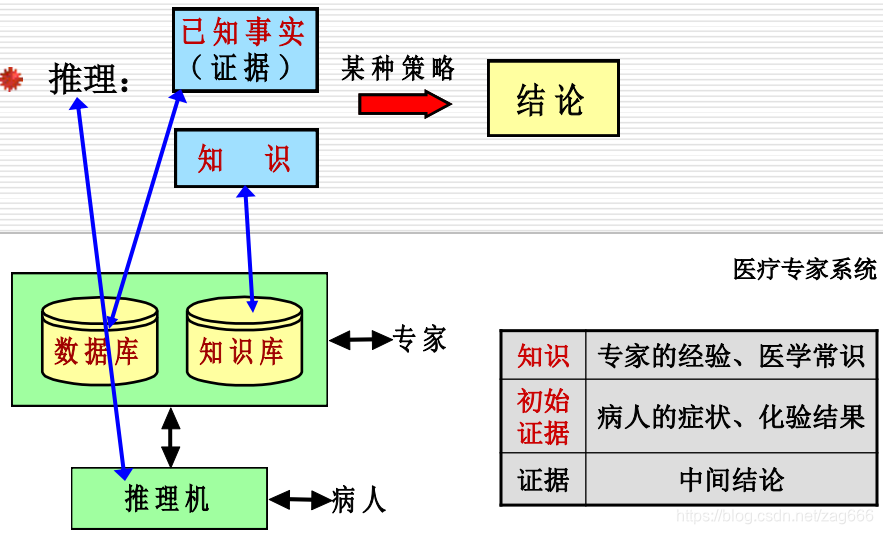
推理的定义
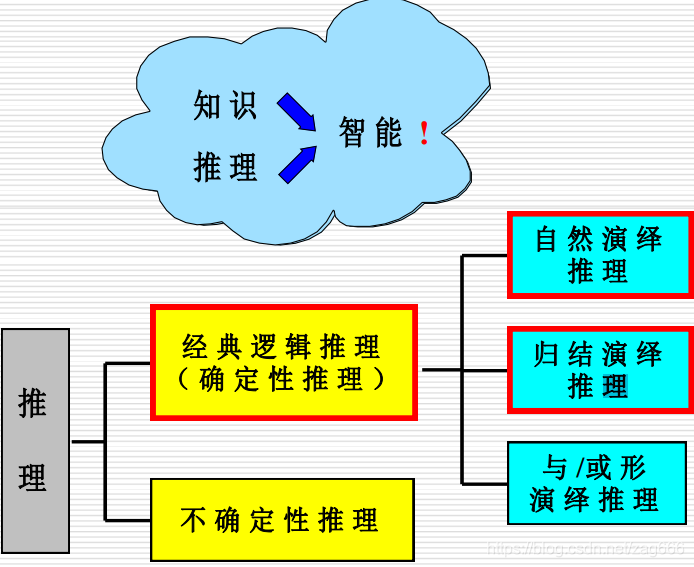
推理方式及其分类
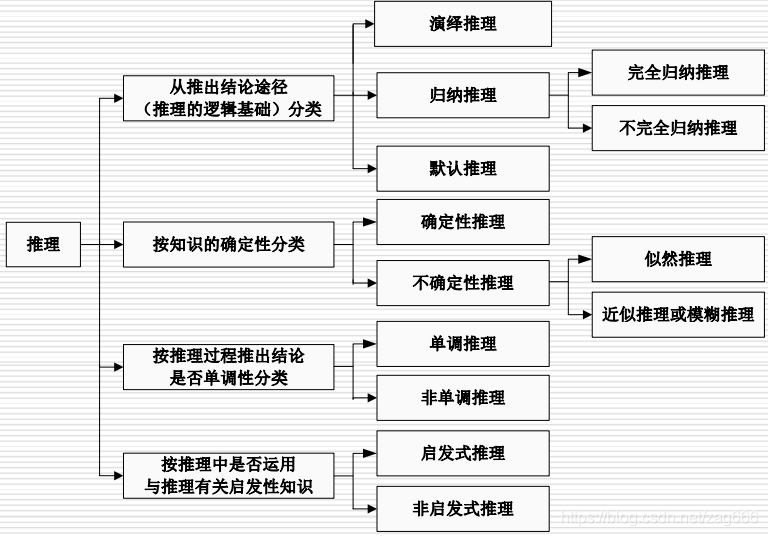
1.演绎推理:一般 → 个体
- 三段论式(三段论法)

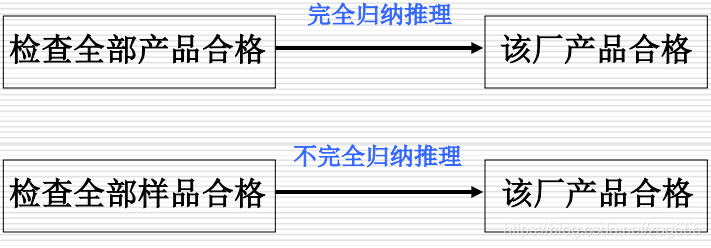
2.归纳推理:个体 → 一般
- 完全归纳推理(必然性推理)
- 不完全归纳推理(非必然性推理)
3.默认推理(缺省推理):知识不完全的情况下假设某些条件已经具备所进行的推理。

1.确定性推理:推理时所用的知识与证据都是确定的,推出的结论也是确定的,其真值或者为真或者为假。
2.不确定性推理:推理时所用的知识与证据不都是确定的,推出的结论也是不确定的。

1.单调推理(基于经典逻辑的演绎推理):随着推理向前推进及新知识的加入,推出的结论越来越接近最终目标。
2.非单调推理(默认推理是非单调推理):由于新知识的加入,不仅没有加强已推出的结论,反而要否定它,使推理退回到前面的某一步,重新开始。
1.启发式推理
2.非启发式推理
启发性知识:与问题有关且能加快推理过程、提高搜索效率的知识。
推理的方向
1.正向推理(事实驱动推理): 已知事实 → 结论
特点:正向推理简单,易实现。但目的性不强,效率低。
2.逆向推理(目标驱动推理):以某个假设目标作为出发点。
特点:不必使用与目标无关的知识,目的性强,同时它还有利于向用户提供解释。但起始目标的选择有盲目性,比正向推理复杂。
3.混合推理:
(1)先正向后逆向:先进行正向推理,帮助选择某个目标,即从已知事实演绎出部分结果,然后再用逆向推理证实该目标或提高其可信度;
(2)先逆向后正向:先假设一个目标进行逆向推理,然后再利用逆向推理中得到的信息进行正向推理,以推出更多的结论。
4.双向推理:正向推理与逆向推理同时进行,且在推理过程中的某一步骤上“碰头”的一种推理。
冲突消解策略
事实与知识的三种匹配情况:
(1)恰好匹配成功(一对一);
(2)不能匹配成功;
(3)多种匹配成功(一对多、多对一、多对多)-------冲突消解
多种冲突消解策略:按针对性排序,按已知事实的新鲜性排序,按匹配度排序,按条件个数排序。
自然演绎推理
自然演绎推理:从一组已知为真的事实出发,运用经典逻辑的推理规则推出结论的过程。
推理规则:P规则、T规则、假言推理、拒取式推理
优点:
表达定理证明过程自然,易理解。
拥有丰富的推理规则,推理过程灵活。
便于嵌入领域启发式知识。
缺点:易产生组合爆炸,得到的中间结论一般呈指数形式递增。
谓词公式化为子句集的方法
原子(atom)谓词公式: 一个不能再分解的命题。
文字(literal):原子谓词公式及其否定。
P :正文字,┐P :负文字。
子句(clause):任何文字的析取式。任何文字本身也都是子句。
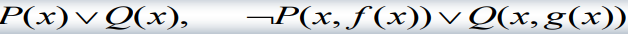
空子句(NIL):不包含任何文字的子句。(空子句是永假的,不可满足的。)
子句集:由子句构成的集合。
合取:∧ 析取:∨


(2)到(3)因为后边的y是约束变元,x是自由变元,所以y变z,x不变。

yz在存在量词后,所以将其设为f,g,删掉存在量词


几个分别析取的子式合取起来

谓词公式不可满足的充要条件是其子句集不可满足。
鲁宾逊归结原理
子句集中子句之间是合取关系(子句内是析取关系),只要有一个子句不可满足,则子句集就不可满足。
鲁宾逊归结原理(消解原理)的基本思想:
检查子句集 S 中是否包含空子句,若包含,则 S 不可满足。
若不包含,在 S 中选择合适的子句进行归结,一旦归结出空子句,就说明 S 是不可满足的。
1.命题逻辑中的归结原理(基子句的归结)
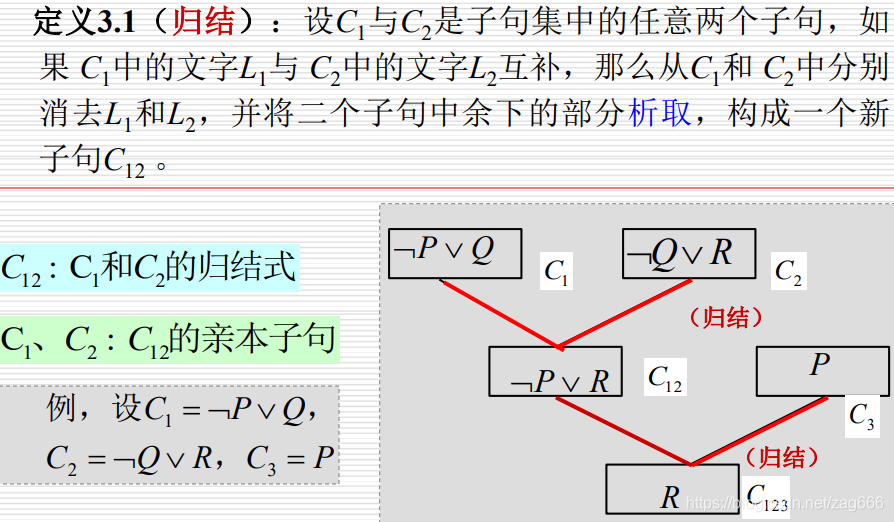
归结式C12是其亲本子句C1与C2的逻辑结论。即如果C1与C2为真,则C12为真。

2.谓词逻辑中的归结原理(含有变量的子句的归结)

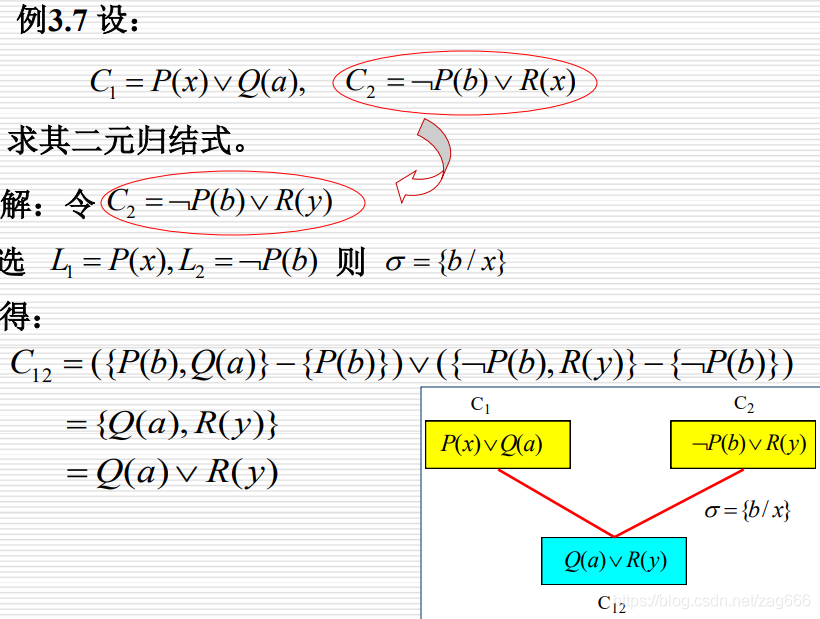
注意:要归结的不能是两个变量,即C2中b变成y就不能归结了

- 对于谓词逻辑,归结式是其亲本子句的逻辑结论。
- 对于一阶谓词逻辑,即若子句集是不可满足的,则必存在一个从该子句集到空子句的归结演绎;若从子句集存在一个到空子句的演绎,则该子句集是
不可满足的。 - 如果没有归结出空子句,则
既不能说 S 不可满足,也不能说 S 是可满足的。
归结反演
应用归结原理证明定理的过程称为归结反演。
用归结反演证明的步骤是:

某公司招聘工作人员,A,B ,C 三人应试,经面试后公司表示如下想法:
(1) 三人中至少录取一人。
(2) 如果录取 A 而不录取 B ,则一定录取 C。
(3) 如果录取 B ,则一定录取 C 。
求证:公司一定录取 C。

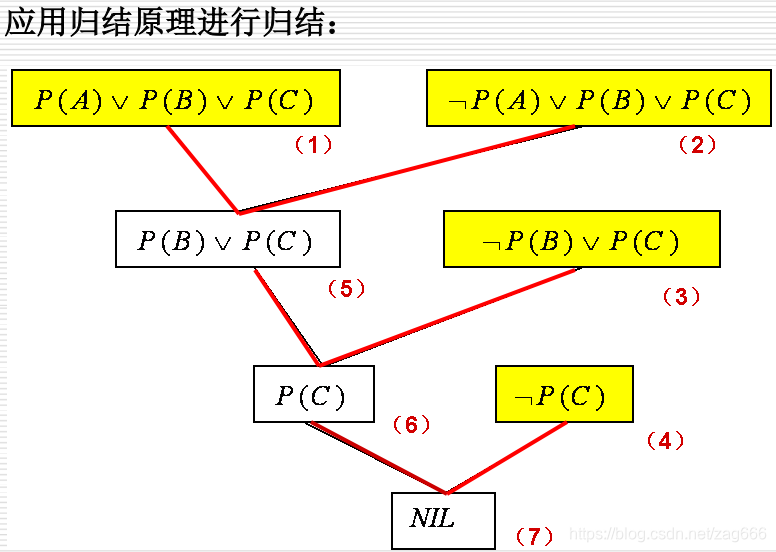

应用归结原理求解问题



