- 1康师傅现身传功 | 直播开讲:MySQL高能技术图谱_尚硅谷 红康主
- 22021华东师范大学软院保研夏令营(可信人工智能大学生夏令营)经验总结_华东师范大学 软件学院夏令营 优营
- 3移植 RT-Thread Nano 到 RISC-V
- 4基于Java微信小程序校园自助打印系统设计和实现(源码+LW+调试文档+讲解等)_java实现的自助打印小程序
- 5openCV3.0 C++ 学习笔记补充(自用 代码+注释)---持续更新 二(51-)
- 62024年前端面试都聊啥?一起来看看,技术总监都拍手叫好_2024年前端面试情况
- 7OpenCV实例(八)车牌字符识别技术(一)模式识别_opencv模式识别
- 8根证书(root certificate)是屬於根证书颁发机构(CA)的公钥证书
- 9Kafka 和 Zookeeper 的 Leader 和 Follower 区别(选举&数据同步)_kafkaleader和follow
- 10tcl命令操作JTAG
GPU通用计算介绍_gpu计算
赞
踩
谈到 GPU (Graphics Processing Unit,图形显示卡)大多数人想到的是游戏、图形渲染等这些词汇,图形处理确实是 GPU 的一大应用场景。然而人们也早已关注到它在通用计算上的巨大潜力,并提出了 GPGPU (General-purpose computing on graphics processing units, 图形处理器上的通用计算) 概念。到随着大数据处理、深度学习的流行,它也在开始在服务器上大行其道。这是因为“同等价格和功耗下,GPU 可以比 CPU 提供多的指令吞吐和内存带宽”,许多业务逐渐开始通过它来进行降本增效。 本文主要讨论 GPU 在通用计算方面的能力,所以不涉图形渲染类的内容。
1. GPU 硬件结构
1.1 概述
GPU 与 CPU 设计的理念不相同,。CPU主要设计用于处理通用计算任务,强调单线程性能、缓存和复杂的控制逻辑,它更适合处理顺序、逻辑密集型任务,如操作系统、办公软件等。GPU的设计理念则专注于并行处理,适用于大规模数据并行计算,如图形渲染、科学计算和深度学习,它通常具有大量的小型核心,专注于高吞吐量的并行计算,以提供对大规模数据集的快速处理。正式由于 GPU 是为高度并行化设计的,因此它拥有更多的晶体管来进行数据处理,而不是数据缓存和流量控制。
下图为典型的 CPU 和 GPU 架构对比,GPU 的每一行一个 control 和 cache 对应有多个 Core,代表着同样指令在同一时刻可由多个 Core 执行,这样并行的设计使 GPU 可以并行执行几千个线程,而其内存访问的延时被计算所缓解。
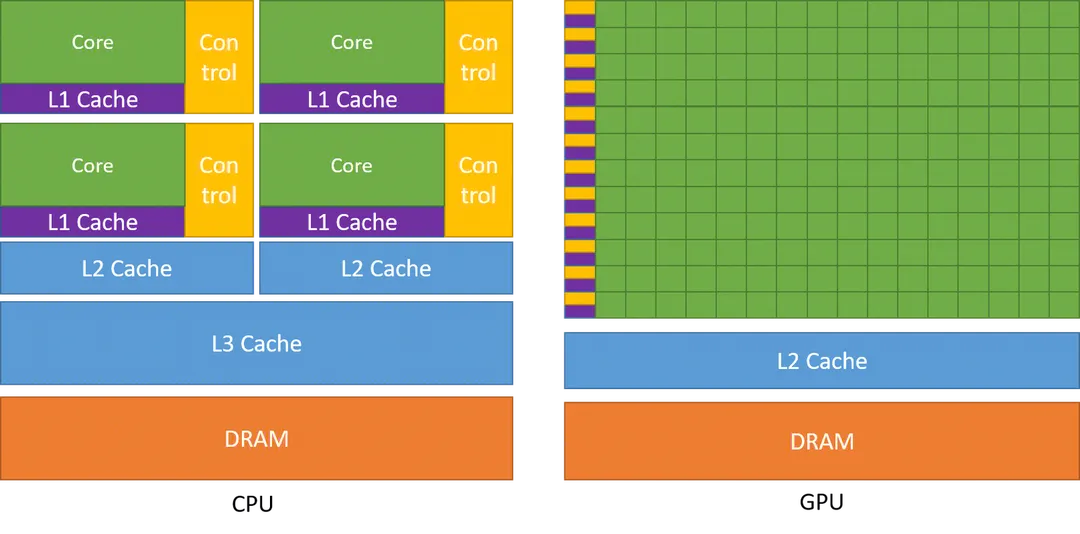
1.2 规格参数
无论是 PCG 123 平台提供的 Tesla T4, 又或者是当前最为强大的 NVIDIA GH100,从 NVIDIA 官网 都可以轻易查询到它的规格参数, 在了解完 GPU 硬件结构后我们就可以对这些参数有更加深刻的理解了。通过 GPU 的规格参数可以了解其许多关键特性和计算能力,这对于我们要利用其进行通用计算至关重要。常见的规格参数包括:
-
浮点数及整数运算能力, 往往用 TFLOPS (Tera Floating-point Operations Per Second, 每秒一万亿次浮点运算)、TOPS(Tera Operations Per Second, 每秒一万亿次操作) 来衡量
-
GPU 架构,如 Turing、Ampere、Hopper 等
-
GPU 计算单元数量,如 CUDA Core 和 Tensor Core 数量
-
显存大小和显存带宽
-
接口类型、最大功耗,及其它各种参数
以下是常见的一些 GPU 规格参数。
| GPU | NVIDIA Tesla P40 | NVIDIA Tesla P100 PCIe 16 GB | NVIDIA Tesla T4 | NVIDIA Tesla V100 PCIe 32 GB | NVIDIA A10 PCIe | NVIDIA A100 PCIe | NVIDIA H100 PCIe |
|---|---|---|---|---|---|---|---|
| GPU model | GP102 | GP100 | TU104 | GV100 | GA102 | GA100 | GH100 |
| 架构 | Pascal | Pascal | Turing | Volta | Ampere | Ampere | Hopper |
| 工艺 | 16 nm | 16 nm | 12 nm | 12 nm | 8 nm | 7 nm | 4 nm |
| 发布时间 | 2016 | 2016 | 2018 | 2018 | 2021 | 2020 | 2022 |
| GPU Memory | 24 GB GDDR5X, 694.3 GB/s | 16 GB HBM2, 732.2 GB/s | 16 GB GDDR6, 320 GB/s | 32 GB HBM2, 897.0 GB/s | 24 GB GDDR6, 600.2GB/s | 40 GB HBM2E, 1,555 GB/s | 80 GB HBM3, 2 TB/s |
| Tensor Core | NA | NA | NA | 320 | 288 | 432 | 528 |
| SMs | 30 | 56 | 40 | 80 | 72 | 108 | 144 |
| 运算能力 | FP32: 12TFLOPs | FP16: 21.2TFLOPS | FP16: 65 TFLOPS | FP16: 112 TFLOPS | FP32: 31.2 TFLOPS | FP64: 9.7 TFLOPS | FP64: 26 TFLOPS |
1.3 NVIDIA GPU 架构演进
NVIDIA 的 GPU 架构随着时间推移也不断演进,比如采用更先进的制程工艺、放入更多的计算单元、引入更多的新功能之类,其发展历程如下表所示。
| 时间 | 架构名 | 制程 | 主要显卡系列 | 主要特性 |
|---|---|---|---|---|
| 2006 | 90nm/80nm/65nm/55nm/40nm | GeForce 8 | CUDA | |
| 2010 | 40nm/28nm | GeForce 400 | SM(Streaming Multiprocessor) | |
| 2012 | 28nm | GeForce 600 | SM 提升 | |
| 2014 | 28nm | GeForce 700 | SM 提升 | |
| 2016 | 16nm/14nm | GeForce 10 series | NVLink | |
| 2017 | 12nm | Tesla V100 | Tensor Core | |
| 2018 | 12nm | GeForce 20 series | Tensor Core 2.0 | |
| 2020 | 8nm/7nm | GeForce 30 series | NVLink 3.0 | |
| 2022 | 5nm | GeForce 40 series | Tensor Core 4.0 | |
| 2022 | 4nm | NVIDIA H100 | NVLink 4.0 |
1.4 GPU 原理图
显卡中真正负责计算的只有和 CPU 大小接近的芯片,即显卡核心,显卡上的其它组件都是为它提供电源、通信等功能的,我们以 NVIDIA GH100 GPU 为例来介绍一下它的硬件结构。
1.4.1 GPU 全局原理图
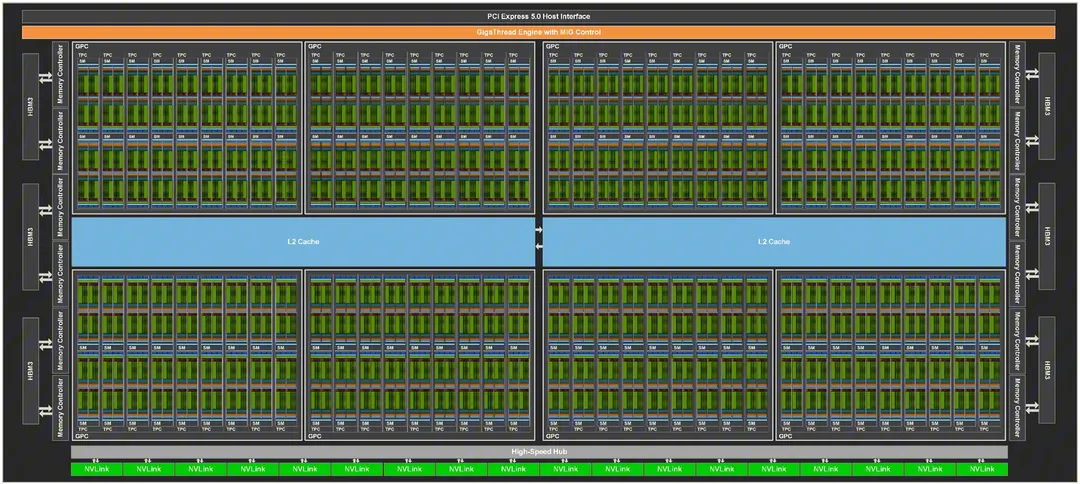
它的完整的实现如下:
-
8 个 GPC (Graphics Processing Cluster, 图形处理集群)
-
每个 GPC 包括 9 个 TPC (Texture Processing Cluster, 纹理处理集群)
-
每个 TPC 包括 2 个 SM (流式多处理器)
-
6 个 HBM3
-
12 个 512 位内存控制器
-
60 MB 二级缓存
-
GigaThread Engine with MIG Control
1.4.2 流式多处理器原理图

对于一个 SM, 它包含:
-
L1 Instruction Cache
-
Tensor Memory Accelerator
-
256 KB L1 Data Cache
-
4 个 Tex
-
4 个 SMP (SM Processing Block)
对于每个 SMP, 它包含:
-
L0 Instruction Cache
-
Wrap Scheduler, 这个模块负责 warp 调度,一个 warp 由 32 个线程组成,warp调度器的指令通过 Dispatch Unit 送到 Cuda Core 执行
-
Dispatch Unit
-
Register File, GPU 寄存器
-
Tensor Core
-
32 个 FP32 CUDA Core
-
16 个 FP64 CUDA Core
-
16 个 INT32 CUDA Core
-
SFU (Special function units), 执行特殊数学运算, 如 sin、cos、log 等
-
8 个 LD/ST (Load/Store), 加载和存储数据
1.4.3 Tensor Core(张量核心)
深度学习的计算瓶颈往往在矩阵乘法,在 BLAS (Basic Linear Algebra Subprograms, 基本线性代数子程序) 中称为 GEMM (General matrix multiply),张量核心就是只做 GEMM 计算的单元。
每个张量核心并行执行运算 D = A * B + C ,其中 A、B、C 和 D 是 4 × 4 矩阵,如下图所示。矩阵乘法输入 A 和 B 是 FP16 矩阵,而累加矩阵 C 和 D 可以是 FP16 或 FP32 矩阵,通常更大的矩阵计算会被拆解为这样小的矩阵乘法。
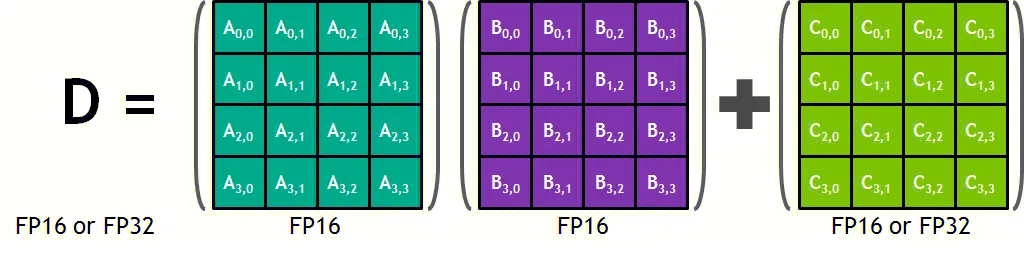
每个张量核心在每个时钟周期执行 64 次浮点 FMA(Fused-Multiply-Add,积和熔加运算) 混合精度运算。
在 H100 中使用了第四代 Tensor Core 架构,除了拥有更高的 GPU Boost 时钟频率,它还支持 FP8、FP16、BF16、TF32、FP64 和 INT8 数据类型。
1.5 GPU 中其它的技术要点
1.5.1 NVLink 与 NVSwitch
当下 AI 和高性能计算领域的算力需求不断增长(尤其是新兴的超大规模参数模型),在这个趋势下对于每个 GPU 之间无缝通信的多节点、多 GPU 系统的需求也与日俱增。在这种情况下可扩展的快速互联必不可少。
NVIDIA NVLink 是一种高速 GPU 互连技术,它通过连接多块 NVIDIA 显卡,以实现显存和性能扩展,从而满足更大的计算工作负载的需求。实现第四代 NVLink 的 H100 可以支持多达 18 个 NVLink 连接,总带宽为 900 GB/s,是 PCIe 5.0 带宽的 7 倍。
NVIDIA NVSwitch 基于 NVLink 的高级通信能力构建,可为计算密集型工作负载提供更高带宽和更低延迟。为了支持高速集合运算,每个 NVSwitch 都有 64 个 NVLink 端口,借助 NVSwitch,NVLink 连接可在节点间扩展,以创建高带宽的多节点 GPU 集群,从而有效地形成数据中心大小的 GPU。通过在服务器外部添加第二层 NVSwitch,NVLink 网络可以连接多达 256 个 GPU,并提供 57.6 TB/s 的多对多带宽,从而快速完成大型 AI 作业。
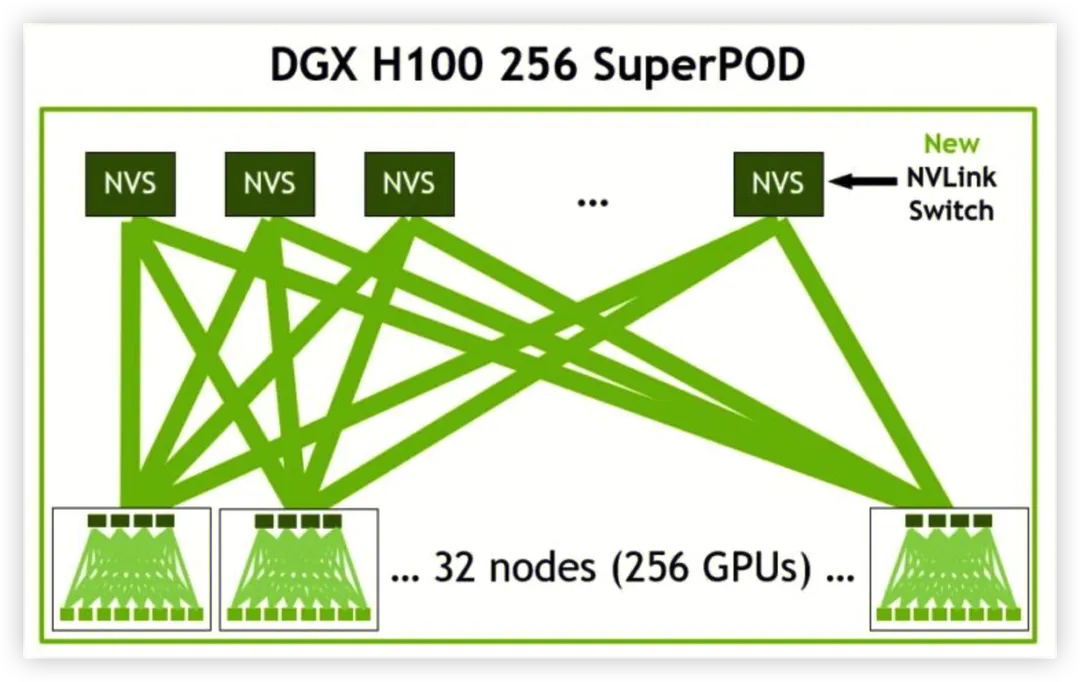

1.5.2 Nvidia Transformer Engine
Transformer 模型是当今从 BERT 到 GPT-3 广泛使用的语言模型的支柱,它们需要大量的计算资源。它们的规模继续呈指数增长,现在达到上万亿个参数,并导致它们的训练时间长达数周甚至更久。 H100 包括一个新的Transformer Engine,它使用软件和定制的 NVIDIA Hopper Tensor Core 技术来加速 Transormer 的 AI 计算。
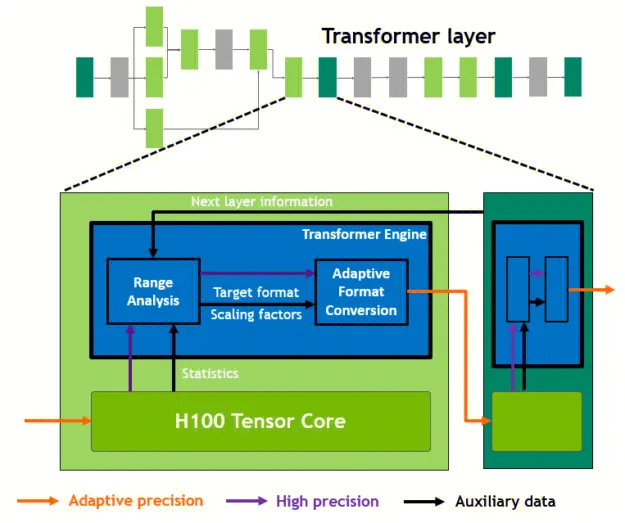
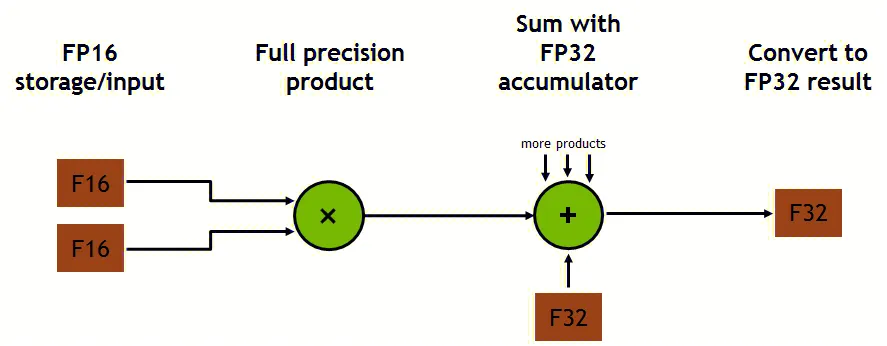
这里提到的加速 AI 计算的方法主要包括混合精度技术。混合精度即指在硬件层面使用更小、更快的数字格式以带来更高的性能,同时也可以保持结果准确性,比如使用 FP16 作为输入,使用 FP32 作为中间结果以保证准确性。
在 Transformer 模型的每一层,Transformer Engine 分析 Tensor Core 产生的输出值的统计数据。了解接下来是哪种类型的神经网络层及其所需的精度后,转换器引擎还会决定在将张量存储到内存之前将其转换为哪种目标格式。为了最佳地使用可用的精度范围,Transformer Engine 还使用从张量统计数据中的的缩放因子将张量数据动态缩放到可表示的范围内。因此每一层都在其需要的范围内精确运行,并以最佳方式进行加速。
1.5.3 DDR、LPDDR、GDDR、HBM
一般的 PC 或服务器使用的都是 DDR 内存 (Double Data Rate Synchronous Dynamic Random Access Memory,双倍数据率同步动态随机存取存储器,简称DDR SDRAM), 关注移动端的同学也了解在低功耗设备会使用 LRDDR (Low Power DDR)。然而 GPU 却更多地使用 GDDR (Graphics Double Data Rate) 或 HBM(High Bandwidth Memory, 高带宽内存) 作为其显存。
GDDR 名字中的 Graphics 就指出其为图形处理器专门优化过,它的内存颗粒区别于 DDR 的 SDRAM, 而是采用了 SGRAM(synchronous graphics random-access memory,同步图形动态随机存取内存),其读取是以 Block 为单位,从减少了读写次数,提升了控制器效率和内存带宽。
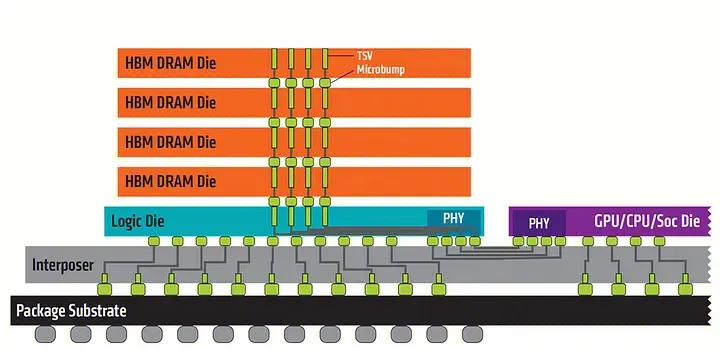
然而业界需要分析的数据集规模越来越大,就需要更大的 GPU 内存容量和带宽。HBM 是一种基于 3D 堆栈工艺的高性能 DRAM。通过该工艺堆积多块 DRAM 裸晶,相比较 DDR 或 GDDR 而言,HBM 有着以更小的体积、更少的功率和更高的带宽,以实现 HBM3 的 H100 SXM5 GPU 为例,它通过支持 80 GB 显存容量和超过 3 TB/秒的显存带宽。
1.5.4 GPU Direct
将数据从存储器加载到 GPU 进行处理的过程历史上一直由 CPU 来控制,然而 GPU 计算数据的速度比 CPU 要快得多,随着数据集地不断增加,对 IO 带宽的需求也随之增加。NIVDIA GPU Direct 是一系列技术,使用它可以让网络适配器和存储驱动器直接读取和写入 GPU 内存, 以减少不必要的内存拷贝和CPU开销, 它包含
-
GPUDirect Storage: 支持本地或远程存储与 GPU 内存之间的直接数据路径GPUDirect Remote Direct Memory Access (RDMA): 使外围 PCIe 设备能够直接访问 GPU 内存

-
GPUDirect Remote Direct Memory Access (RDMA): 使外围 PCIe 设备能够直接访问 GPU 内存
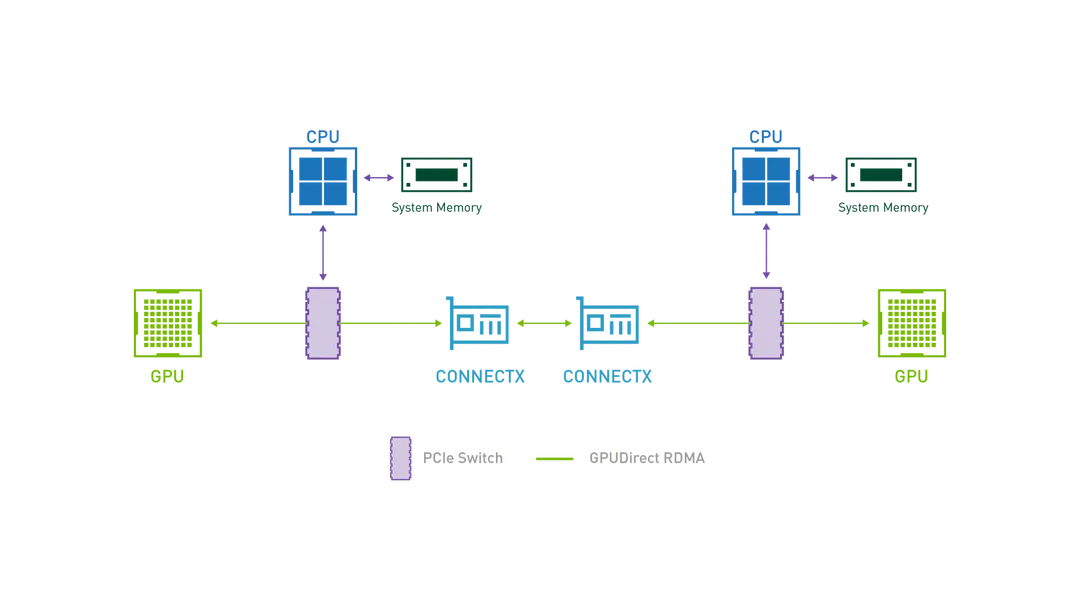
-
GPUDirect Peer to Peer (P2P): 支持 GPU 到 GPU 的复制以及直接通过内存结构(PCIe、NVLink)加载和存储
-
GPUDirect Video: 为帧采集器、视频切换器、HD-SDI 捕获和 CameraLink 设备等基于帧的设备提供优化的管道
1.6 内存延迟带来的问题与 CPU、GPU 的解决方案
为了实现“同等价格和功耗下,GPU 可以比 CPU 提供多的指令吞吐和内存带宽”,那么代价是什么呢?回答这个问题之前,让我们先探究一个常被忽略的事实,即物理定律和硬件很大程度上决定了我们对于这些机器的编程方式。
从更贴近我们的 CPU 说起吧,当下 CPU 的时钟频率往往能达到 3G Hz 以上,这个速度非常之快,以至于一个时钟周期内就连光也只能传播 10 cm。电流在硅中传播的速度更慢,根据经验,一个时钟周期电流只能移动 20 mm。 CPU 距离内存在通常在 100mm 左右,只是让电流从一端到另一端什么都不做,并按最理想的直线距离访问也至少需要 5 个时钟周期了,实际情况下 (电流的传输时间以及对 DDR 晶体管的访问) 内存延迟往往可以达到 100 ns 左右。
以 Intel Xeon 8280 和配套的内存为例, 它的内存带宽为 131 GB/s, 内存延迟为 89 ns,我们让它来执行下面这一段程。
- void daxpy(int n, double alpha, double *x, double *y) {
- for (int i = 0; i < n; i++) {
- y[i] = alpha * x[i] + y[i];
- }
- }
其数据加载与计算的流程如下, 由于加载 y 并不依赖与 x, 所以程序可以几乎同时请求对于他们的加载,经历较长的内存延迟后 x 和 y 被成功加载,并随后执行逻辑运算。与计算延迟相比,这里的内存延迟要大得多。
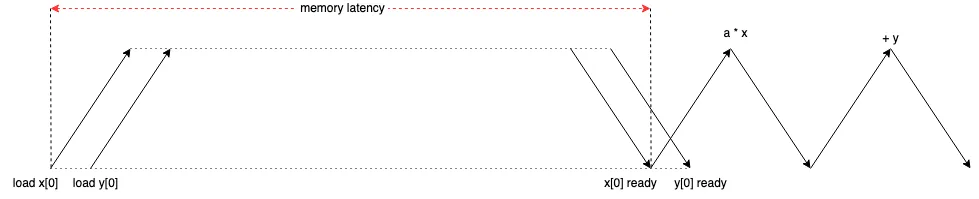
既然最大带宽为 131 GB/s, 那么相当于每 89 ns 可传输 11659 byte, 可我们这段程序每次却只传输 16 个 byte, 带宽利用率只有 0.14%,如果我们都不能让带宽充分利用的话,那 CPU 或 GPU 拥有再高的 FLOPS 也毫无意义。那我们不妨对这里进行优化,既然一次传入 16 个 byte 对内存使用效率太低的话,那我们就多传几个,这个带宽允许我们一次传输 11659/16=729 个迭代所需的变量数据,一种常见的方式为 Loop Unrolling (循环展开), 大部分情况编译器会自动优化完成。
- void daxpy(int n, double alpha, double *x, double *y) {
- for (int i = 0; i < n; i += 8) {
- y[i + 0] = alpha * x[i + 0] + y[i + 0];
- y[i + 1] = alpha * x[i + 1] + y[i + 1];
- y[i + 2] = alpha * x[i + 2] + y[i + 2];
- y[i + 3] = alpha * x[i + 3] + y[i + 3];
- y[i + 4] = alpha * x[i + 4] + y[i + 4];
- y[i + 5] = alpha * x[i + 5] + y[i + 5];
- y[i + 6] = alpha * x[i + 6] + y[i + 6];
- y[i + 7] = alpha * x[i + 7] + y[i + 7];
- }
- }
然而一方面编译器几乎不会展开一个循环数百次,另一方面单线程也很难处理数百个待完成的 load,这受限于许多其它硬件限制。
另外一种常见的方式为使用更多的线程来处理 (这与 Loop Unroling 并不冲突,可以一起使用),就比如创建 729 个线程,所幸 Intel Xeon 8280 有 896 个 available Threads。
现在终于能够充分利用内存带宽了,可是想充分发挥 CPU 的计算性能仍然是具有挑战的事情。仍然以 Intel Xeon 8280 为例,它的算力达到 2192 GFLOP, 它的带宽满载时每秒可以传输 163.75 亿个 FP64, 也就是除非对每个数据执行 134 次以上的操作 (这里的算力与带宽之比就是Compute Intensity, 即计算强度),否则 CPU 就会空闲下来,实际上并没有那么多的算法可以做到这些(内存的带宽不足,不能匹配上cpu的算力,实际上难以将cpu的算力充分利用) 。当然为了提升 CPU 使用率,一方面可以通过内部的多级缓存(减少cpu和内存之间的数据传输的频次,将数据存放在缓存中,能够缓解内存带宽不足的问题),利用程序的局部性原理,也有较好的效果,另一方面选择也可以选择提升内存带宽,这就是为何 HBM 在显卡上应用愈发广泛的原因。我们对比一下在以上示例中的常见 CPU 与 GPU 的参数。
| 计算类型 | Intel Xeon 8280 | NVIDIA A100 |
|---|---|---|
| FP64 GFLOP | 2190 | 195000 |
| 内存(显存)带宽 GB/sec | 131 | 1555 |
| 内存延迟 ns | 89 | 404 |
| 计算强度 | 134 | 100 |
| 内存(显存)延迟期间传输 16 byte 的内存使用率 | 0.14 % | 0.0025 % |
| 填满内存(显存)带宽所需线程数量 | 729 | 39264 |
| 可用线程数量 (Threads available) | 896 | 221184 |
CPU 和 GPU 的区别,主要就体现在如何解决内存延迟带来的带宽使用效率问题。其中 CPU 关注减少单个线程本身延迟问题,它总期望一个线程来完成主要工作,线程从一个切换到另一个是非常昂贵的。而 GPU 设计师把所有资源都投入到更多的线程中,而不是减少延迟。它通过多线程并发处理来充分利用带宽,来抵消内存延迟带来的带宽效率问题。
2. GPU 的通用计算
2.1 CUDA 介绍
NVIDIA 在 2006 年就推出了 CUDA (Compute Unified Device Architecture,统一计算架构),这是一种通用并行计算平台和编程模型,它利用 NVIDIA GPU 中的并行计算引擎解决许多复杂的计算问题。CUDA 附带一个软件环境,允许开发人员使用 C++ 作为高级编程语言,也支持其他语言(如 C、FORTRAN、Java...)、应用程序编程接口(如 DirectCompute)。
CUDA 并行编程模型的核心是如下的三个关键的抽象
-
线程组的层次结构
-
共享内存
-
屏障同步
它们作为最小的语言扩展集简单地暴露给程序员。这些抽象提供细粒度的数据并行性和线程并行性。
它们指导我们将问题划分为可由块内所有线程并行协作解决的细小的部分。这种分解通过允许线程在解决每个子问题时进行协作来保留语言表达能力,同时实现自动可扩展性。每个线程块都可以在 GPU 内的任何可用多处理器上以任何顺序进行调度,以便编译后的 CUDA 程序可以在任意数量的多处理器上执行,如下图所示。

这种可扩展的编程模型允许 GPU 架构通过简单地扩展多处理器和内存分区的数量来适配更加广泛的应用场景。
2.2 SIMT 与 SIMD
SIMT 和 SIMD 都是常见的并行处理模型,在 GPU 中也广泛地使用了这些方法。
SIMT (Single Instruction Multiple Thread) 为单指令多线程,假设有两个等长的数组,需要每个元素一一对应相加。那么 SIMT 的思想就是给每个元素分配一个线程,那么一个线程只需要完成一个元素的加法,所有线程并发执行完成后,两个数组的相加就完成了。SIMT 往往被实现为一个具有多个 SIMT 核心的系统,每个 SIMT 核心都有它自己的寄存器、数据 Cache、ALU (Arithmetic logic unit,算数逻辑单元),但是它只有一个 Program Counter 寄存器、一个指令 Cache 和一个译码器,指令被同时广播给所有的 SIMT 核。
SIMD (Single Instruction Multiple Data) 为单指令多数据,即在一条指令完成多个数据的计算。比如通常一次加法操作只能完成一个整数的加法,而通过 SIMD 指令,一个次可以完成多个整数的加法。只不过这就需要增加 ALU 单元的数量,同时也需要增加同一个功能单元的数据通路数量。
之前 GPU 是主要是进行图形处理的,运算的对象要么是颜色 RGBA,要么是坐标 XYZW,都是向量。于是早期的 GPU 都是对一个 4 单位的向量进行操作,在此架构下,编译器会尽可能把数据打包成 vec4 来进行计算。但是随着 GPU 通用计算的发展,计算变得越来越复杂,数据并不一定能够打包成 vec4,这就可能会导致性能的浪费。所以现代 GPU 都改进为 SIMT,这在可编程性上也带来了更大的优势。
2.3 kernel
一个 CUDA 程序的可以分为两个部分,
-
在 CPU 上运行的 Host 程序;
-
在 GPU 上运行的 Device 程序。
两者拥有各自的存储器。GPU 上运行的函数又被叫做 kernel 函数,通过 global 关键字声明,如下示例代码将两个大小为 N 的向量 A 和 B 相加,并将结果存储到向量 C 中。
- // Kernel definition
- __global__ void VecAdd(float* A, float* B, float* C)
- {
- int i = threadIdx.x;
- C[i] = A[i] + B[i];
- }
-
- int main()
- {
- ...
- // Kernel invocation with N threads
- VecAdd<<<1, N>>>(A, B, C);
- ...
- }
Host 程序在调用 Device 程序时,可以通过 <<<...>>> 中的参数提定执行该 kernel 的 CUDA threads 的数量。需要注意,当调用 kernel 时,由 N 个不同的 CUDA 线程并行执行 N 次,而不是像常规 C++ 函数那样只执行一次。在这里执行的 N 个 VecAdd() 线程中的每一个都执行一对加法。每个执行内核的线程都被赋予一个唯一的线程 ID,该 ID 可通过内置变量在内核中访问。
2.4 warp
warp 是 SM 调度和执行的基础概念,理解它对优化 CUDA 程序有很重要的意义。
在 GPU 中一个 Kernel 函数会创建多个线程,每个线程都独立执行相同的指令。一个 SM 可以同时驻留和执行多个线程块。每个线程块会被映射为多个包含 32 个线程的 warp。 这个 warp 中的 32 个 thread 是一起工作的,执行相同的指令。从开发者角度来看,Thread Block 中所有的 thread 是同时运行的,但是真正同一时刻运行的 thread 只有 32 个。

这里就有一个 Warp 调度的流程,每个 SM 中具备 Warp Scheduler 和 Dispatch Unit 用来调度不同的 Warp。下图中可以注意到每个 SM 内有多个(不同的 GPU 数量不一样,下图所示为 2 个) Warp Scheduler 和多个 Dispatch Unit. 这意味着,同一时刻,会并发运行多个 warp,每个 warp 会被分发到一组 CUDA Core、或一组 load/store 单元、或一组 SFU、或 Tensor Core,且每次分发只执行一条指令,而 Warp Scheduler 维护了多个(比如数十个)的 Warp 状态。

知道 Warp 概念后,就不得不提 Warp Divergence。我们先看下面这段代码:
- __global__ void mathKernel1(float *c) {
- int tid = blockIdx.x * blockDim.x + threadIdx.x;
- float a, b;
- a = b = 0.0f;
- if (tid % 2 == 0) {
- a = 100.0f;
- } else {
- b = 200.0f;
- }
- c[tid] = a + b;
- }
对于这段代码,在一个 warp 中,奇数位的 thread 会执行 b = 200.0f;,而偶数位的 thread 会执行 a = 100.0f;。如果是这段代码是执行在 CPU 上的,那么就会产生条件转移指令,不同分支的线程遇到该条件转移指令,会跳转到不同的位置继续执行指令,而且 CPU 端有复杂的分支预测器来减少分支跳转的开销。但是 GPU 上是没有这些复杂的分支处理机制的,所以 GPU 在执行时,warp 中所有 thread 执行的指令是一样的,唯一不同的是,当遇到条件分支,如果满足该条件,就继续执行对应的指令,如果不满足该条件,该 thread 就会阻塞,直到其他满足该条件的 thread 执行完这段条件语句,上述现象就是 Warp Divergence, 见下图。

发生 Warp Divergence 的时候会造成性能的下降,所以针对上面代码,我们可以进行如下改造,奇数位的 warp 会执行 b = 200.0f;,而偶数位的 warp 会执行 a = 100.0f;:
- __global__ void mathKernel2(void) {
- int tid = blockIdx.x * blockDim.x + threadIdx.x;
- float a, b;
- a = b = 0.0f;
- if ((tid / warpSize) % 2 == 0) {
- a = 100.0f;
- } else {
- b = 200.0f;
- }
- c[tid] = a + b;
- }
上面提到 GPU 没有复杂的分支处理机制,这是有原因的。CPU 并行和 GPU 并行都是为了提升程序的性能。其中 CPU 注重的是延迟,所以 CPU 单核的性能非常强劲,这也造就了 CPU 的硬件机制比较复杂(大量的设备在控制单元和寄存器单元,从而减少跟内存的数据交互,减少延迟)。而 GPU 注重的是 吞吐量,所以 GPU 单核的性能不是很强劲,但是核的数目要远远超过 CPU,以此保证总的吞吐量远远超过 CPU(大量的计算核心不断的跟内存获取数据,从而整体上将内存的带宽吞吐提升上去)。
GPU 不同于 CPU 的一个特点是线程切换是极其迅速的。这是因为每个线程和线程块使用的资源是直接基于硬件资源保存的,而不是先把寄存器内存保存到内存,再从内存加载新线程的信息到寄存器然后再执行。这里会导致几注意点:
-
SM 会在当前 warp 处于某些等待时(比如当前 warp 内的线程在读取 global memory,这可能需要数百个时钟周期),那这时会切换一个新的 warp 进行执行,从而可以显著提升硬件利用率和执行性能。
-
虽然 SM 同时只能执行多个(数量取决于具体的 GPU) warp,但是应该有足够的 warp 驻留用于切换才能保证性能。每个线程块的线程数、每个 SM 能同时执行的线程块数量上限是可以通过 CUDA 提供接口进行查询的。但由于每个线程和线程块都是使用了实打实的寄存器和 shared memory硬件资源,而硬件资源是有限的。因此每个线程和线程块的资源使用量决定了实际每个线程块包含的线程数和每个 SM 能同时执行的线程块数量。实际的程序要比较仔细规划每个线程块的线程数,每个线程和线程块使用的寄存器和shared memory 资源,从而保证SM有足够的warp同时执行。
GPU 对于计算任务的分配任务一个时钟周期只能进行一次。为了提升硬件使用效率,分配的计算任务一般需要多个时钟周期执行。比如当我们可以将 kernel 视为一系列指令。假设下一条指令是一个 INT32 操作。GPU 将一个 warp 32 个线程dispatch 到 16 个(而不是32个) INT32 算术单元以同时执行指令,这是因为从前面 SM 图中可以看到每个 SM 子块只有 16 个 FP32 这也使得 warp 执行每条 INT32指令实际需要 2 个时钟周期才能完成。同理,如果是 FP32, 则只需要一个时钟周期。
2.5 线程的层次结构
CUDA 中的线程组织为三个层次
-
Thread: 线程
-
Thread Block: 线程块, 即线程的集合
-
Grid: 网格, 即线程块的集合

由于一个 Thread Block 的所有线程都应该驻留在同一个 SM (流式多处理器) 核心上,并且共享该核心的有限内存资源,在当前的 GPU 上一个线程块最多可包含 1024 个线程。所以需要采用这种多级结构来组织线程。在上图中,Grid 中 Thread Block 的数量通常由正在处理的数据大小决定。
以下为两个大小为 N x N 的矩阵 A 和 B 相加,并将结果存储到矩阵 C 中的代码示例:
- // Kernel 定义
- __global__ void MatAdd(float A[N][N], float B[N][N],
- float C[N][N])
- {
- // 这里需要区分线程的索引和线程 ID.
- // threadIdx 为一个三维向量,它可以标识线程索引,但同一个 Grid 中不同的 Thread Block 会有相同的索引,此时为了让个线程协作处理当前数据,那么就需要一个 Grip 下全局唯一的一个标识,即线程 ID, 线程 ID 往往是该线程索引结合它所在的 Thread Blcok 的位置信息来进行计算的。如下即为对于二维情况的处理。
- int i = blockIdx.x * blockDim.x + threadIdx.x;
- int j = blockIdx.y * blockDim.y + threadIdx.y;
- if (i < N && j < N)
- C[i][j] = A[i][j] + B[i][j];
- }
-
- int main()
- {
- ...
- // 定义一个 16 * 16 大小的 Thread Block
- dim3 threadsPerBlock(16, 16);
- // 这里为简单起见,此假设每个维度中每个网格的线程数可以被该维度中每个块的线程数整除
- dim3 numBlocks(N / threadsPerBlock.x, N / threadsPerBlock.y);
- MatAdd<<<numBlocks, threadsPerBlock>>>(A, B, C);
- ...
- }

另外,在 NVIDIA Compute Capability 9.0 中引入了一个可选的层次结构,叫做 Thread Block Clusters(线程块簇),如同 Thread Block 保证其中的线程在同一个 SM 上调度那样,Thread Block Clusters 也保证其中的 Thread Block 在同一个 GPC 上调度。

以上的线程层次结构与其对应的硬件结构是这样的。
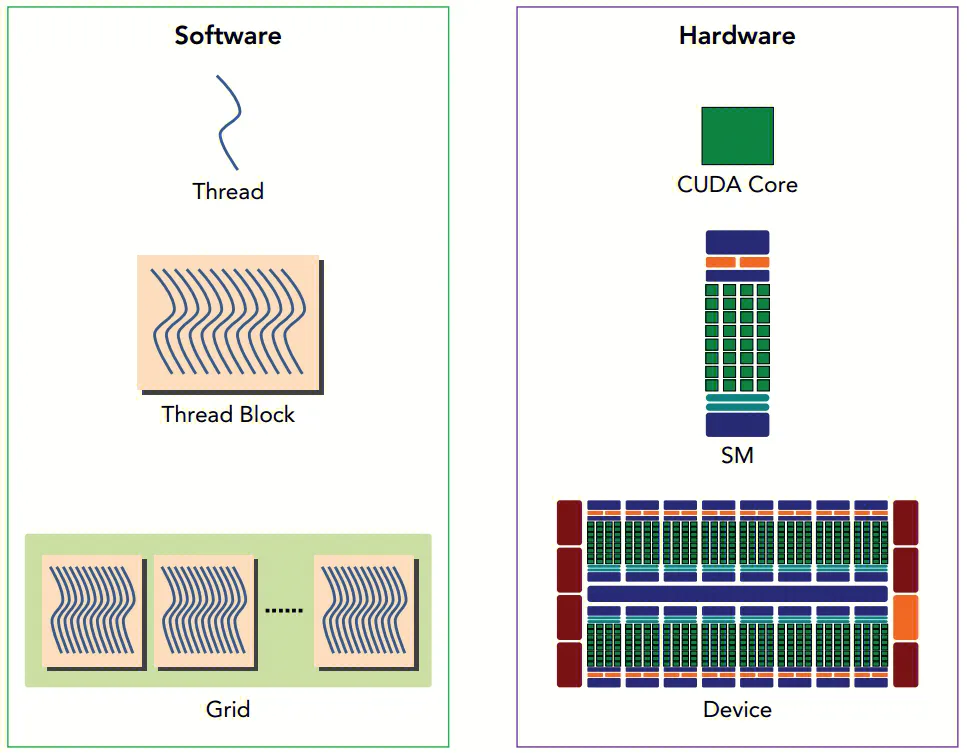
2.6 共享内存
CUDA 的线程在执行期间可以从多个内存空间访问数据。
-
每个线程都有私有的本地内存。
-
每个线程块都具有对该 Thread Block 的所有线程可见的共享内存,并且与该 Thread Block 具有相同的生命周期。
-
Thread Block Clusters 中的 Thread Block 可以对彼此的共享内存执行读、写和原子操作。
-
所有线程都可以访问相同的全局内存。
还有两个额外的只读内存空间可供所有线程访问:
-
常量内存空间
-
纹理内存空间

2.7 CPU 与 GPU 的交互
CUDA 编程模型约定 Device 侧执行 kernel, 其余部分则在 Host 上执行。并且 Device 和 Host 都在 DRAM 中维护自己独立的内存空间,分别称为 host memory(主机内存) 和 device memory (设备内存)。因此程序通过调用 CUDA 运行时来管理对 kernel 可见的全局内存空间、常量内存空间和纹理内存空间。这包括 device 内存分配和释放以及 host 和 device 内存之间的数据传输。

那么典型的 CUDA 程序的执行流程如下:
-
分配 host 内存,并进行数据初始化
-
分配 device 内存,并从 host 将数据拷贝到 device 上
-
调用 CUDA 的核函数在 device 上完成指定的运算
-
将 device 上的运算结果拷贝到 host 上
-
释放 device 和 host 上分配的内存
这里给出一个简单的只用一个 Thread 进行向量点积的例子:
- #include <iostream>
-
- __global__ void vector_dot_product(float *out, float *vec1, float *vec2, int vec_len) {
- float sum = 0;
- for (int i = 0; i < vec_len; i++) {
- sum += vec1[i] * vec2[i];
- }
- *out = sum;
- }
-
- #define VECTOR_LENGTH 256
-
- void test_vec_dot_product() {
- int emb_bytes = sizeof(float) * VECTOR_LENGTH;
-
- // 初始化 host 内存
- auto *vec1 = (float *) malloc(emb_bytes);
- auto *vec2 = (float *) malloc(emb_bytes);
- auto *out = (float *) malloc(sizeof(float));
- for (int i = 0; i < VECTOR_LENGTH; i++) {
- vec1[i] = 3.0f;
- vec2[i] = 2.0f;
- }
-
- // 初始化 device 内存
- float *d_vec1, *d_vec2, *d_out;
- cudaMalloc((void **) &d_vec1, emb_bytes);
- cudaMalloc((void **) &d_vec2, emb_bytes);
- cudaMalloc((void **) &d_out, sizeof(float));
-
- // 将 host 内存 copy 到 device
- cudaMemcpy(d_vec1, vec1, emb_bytes, cudaMemcpyHostToDevice);
- cudaMemcpy(d_vec2, vec2, emb_bytes, cudaMemcpyHostToDevice);
-
- // 执行点乘
- vector_dot_product<<<1, 1>>>(d_out, d_vec1, d_vec2, VECTOR_LENGTH);
- // 将结果 copy 出来
- cudaMemcpy(out, d_out, sizeof(float), cudaMemcpyDeviceToHost);
- std::cout << "result :" << *out << std::endl;
-
- // 释放内存
- cudaFree(d_vec1);
- cudaFree(d_vec2);
- cudaFree(d_out);
- free(vec1);
- free(vec2);
- free(out);
- }
-
- int main() {
- test_vec_dot_product();
- return 0;
- }

在特定的环境下可以使用统一内存,上面的程序就可以被简化一些
3. GPU 通用计算使用
3.1 业界在 GPU 通用计算上的使用
在介绍完 GPU 出色的通用计算能力后,自然容易想到其应用场景。除了图形渲染、音视频转码外,其它常用的使用方式包括:
-
AI 训练及推理
-
加密货币的挖掘
-
科学计算领域: 如天体物理学、分子动力学、流体力学
-
数学领域: 如线性代数运算
-
特定算法加速: 如 AES 加解密、最短路径算法、动态规划算法 (通过 DPX instructions 进行加速)
-
半导体制造: 如 NVIDIA 提供的光刻计算库 cuLitho 可以将计算光刻速度将提升 40 倍,GPU 加速后生产光掩模的计算光刻工作用时可以从几周减少到八小时,与此同时功耗降低 9 倍。
3.2 如何进行 CUDA 编程
要进行 CUDA 编程,较为常用的方法在拥有 GPU 和 NVIDIA 驱动的环境下,使用 C++ 调用 CUDA 库即可。CUDA 源文件采用后缀 .cu, 其编写方法类似于标准 C、C++ 语言,编写完后可通过 nvcc (CUDA 的编译器) 进行编译。
这里将给出一些常见的 CUDA 功能,也同时是后文中小说业务使用的一些功能。
3.2.1 展示 GPU 设备信息
该功能不涉及任何其科学计算,只是直接打印当前 CUDA 设备的一些基础信息, 如 SM 的数量, Thread 的数量之类的信息。
- #include <iostream>
-
- // 展示设备属性
- int ShowDeviceProperty() {
- const int dev = 0;
- cudaDeviceProp dev_prop{};
- auto cuda_err = cudaGetDeviceProperties(&dev_prop, dev);
- if (cuda_err != cudaSuccess) {
- std::cout << "cuda get device properties fail: " << static_cast<int>(cuda_err);
- return -1;
- }
- std::cout << "GPU device " << dev << ": " << dev_prop.name << std::endl;
- std::cout << "SM num: " << dev_prop.multiProcessorCount << std::endl;
- std::cout << "shared mem per block: " << static_cast<float>(dev_prop.sharedMemPerBlock) / 1024.0 << " KB"
- << std::endl;
- std::cout << "max thread num per block: " << dev_prop.maxThreadsPerBlock << std::endl;
- std::cout << "max thread num per SM: " << dev_prop.maxThreadsPerMultiProcessor << std::endl;
- std::cout << "max wrap num per SM: " << dev_prop.maxThreadsPerMultiProcessor / 32 << std::endl;
- return 0;
- }
-
- int main() { return ShowDeviceProperty(); }

3.2.2 通过 kernel 计算向量加法
这里定义了自己创建的 kernel 函数 DeviceVecAdd, 用于进行两个向量的加法。
如下公式即为本例函数所实现的内容。
- #include <iostream>
-
- __global__ void DeviceVecAdd(int *vec_out, const int *vec_a, const int *vec_b) {
- size_t i = blockIdx.x;
- vec_out[i] = vec_a[i] + vec_b[i];
- }
-
- int VecAdd(int *vec_out, const int *vec_a, const int *vec_b, int vec_len) {
- // 在 device 上分配内存空间
- int *dev_vec_a, *dev_vec_b;
- size_t vec_size = sizeof(int) * vec_len;
- auto cuda_err = cudaMalloc(&dev_vec_a, vec_size);
- if (cuda_err != cudaSuccess) {
- std::cout << "cuda malloc fail:" << static_cast<int>(cuda_err);
- return -1;
- }
- cuda_err = cudaMalloc(&dev_vec_b, vec_size);
- if (cuda_err != cudaSuccess) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -2;
- }
-
- // 将数据复制到 device
- cuda_err = cudaMemcpy(dev_vec_a, vec_a, vec_size, cudaMemcpyHostToDevice);
- if (cuda_err != cudaSuccess) {
- std::cout << "cuda mem copy fail: " << static_cast<int>(cuda_err);
- return -3;
- }
- cuda_err = cudaMemcpy(dev_vec_b, vec_b, vec_size, cudaMemcpyHostToDevice);
- if (cuda_err != cudaSuccess) {
- std::cout << "cuda mem copy fail: " << static_cast<int>(cuda_err);
- return -4;
- }
-
- // 执行计算
- int *dev_vec_out;
- cuda_err = cudaMalloc(&dev_vec_out, vec_size);
- if (cuda_err != cudaSuccess) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -5;
- }
-
- DeviceVecAdd<<<vec_len, 1>>>(dev_vec_out, dev_vec_a, dev_vec_b);
- // 拷贝出结果数据
- cuda_err = cudaMemcpy(vec_out, dev_vec_out, vec_size, cudaMemcpyDeviceToHost);
- if (cuda_err != cudaSuccess) {
- return -6;
- }
-
- // 清理 device 内存
- cudaFree(dev_vec_a);
- cudaFree(dev_vec_b);
- cudaFree(dev_vec_out);
- return 0;
- }
-
- int main() {
- // 初始化输入数据
- const int vec_len = 4;
- int vec_a[vec_len] = {1, 2, 3, 4};
- int vec_b[vec_len] = {5, 6, 7, 8};
- int vec_out[vec_len] = {0, 0, 0, 0};
-
- // 执行计算
- auto err = VecAdd(vec_out, vec_a, vec_b, vec_len);
- if (err != 0) {
- return err;
- }
-
- // 打印结果
- for (auto &num : vec_out) {
- std::cout << num << ", ";
- }
- }

3.2.3 通过 cuBLAS 库进行矩阵乘法
cuBLAS (CUDA 基本线性代数子程序, CUDA Basic Linear Algebra Subroutine) 库基于 NVIDIA CUDA 运行时的 BLAS 的实现, 并允许调用 GPU 计算资源进行运算处理,它包含了如 cuBLAS API 、cuBLASXt API、cuBLASLt API 的多组 API, 具体详情可以参考这里。cuBLAS 不仅包含了大量的线性代数计算函数,其性能相比于一般开发者所写的 kernel 也更具性能优势。如下示例即为使用 cuBLAS API 进行矩阵间相乘的运算。
我们现在拥有如下的两个矩阵。并且希望计算两个矩阵的乘法。

但在 cuBLAS 中,默认的矩阵存储方式采用的是列存储(源于 Pascal 语言), 虽然相关函数内提供参数允许传入行存储的矩阵,但这会带来一定的性能损失。
考虑到线性代数中如下的公式:

那么我们只需要计算如下的公式即可:

那么显然
- #include <iostream>
-
- #include "cublas_v2.h"
- #include "cublas_api.h"
-
- // 执行矩阵相乘
- int CublasGEMM(float *matrix_result, const cublasHandle_t &handle, const float *matrix_a, const float *matrix_b, int m,
- int n, int k) {
- // 在 device 开辟显存
- float *dev_matrix_a, *dev_matrix_b;
- size_t float_size = sizeof(float);
- auto cuda_err = cudaMalloc((void **)&dev_matrix_a, m * k * float_size);
- if (cuda_err != 0) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -1;
- }
- cuda_err = cudaMalloc((void **)&dev_matrix_b, k * n * float_size);
- if (cuda_err != 0) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -2;
- }
-
- // 将数据拷贝到显存
- auto cublas_err = cublasSetVector(m * k, int(float_size), matrix_a, 1, dev_matrix_a, 1);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas set vector fail: " << static_cast<int>(cublas_err);
- return -3;
- }
- cublas_err = cublasSetVector(k * n, int(float_size), matrix_b, 1, dev_matrix_b, 1);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas set vector fail: " << static_cast<int>(cublas_err);
- return -4;
- }
-
- // 同步数据
- cudaDeviceSynchronize();
-
- // 为矩阵相乘结果开辟显存
- float *dev_score_vec;
- cuda_err = cudaMalloc((void **)&dev_score_vec, m * n * float_size);
- if (cuda_err != cudaSuccess) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -5;
- }
-
- // GEMM, 参数说明见 https://docs.nvidia.com/cuda/cublas/
- float a = 1;
- float b = 0;
- cublas_err = cublasSgemm(
- // cublas 库上下文句柄
- handle,
- // 矩阵 A 属性参数, 是否转置
- CUBLAS_OP_N,
- // 矩阵 B 属性参数, 是否转置
- CUBLAS_OP_N,
- // 矩阵 A 和矩阵 C 的行数
- n,
- // 矩阵 B 和矩阵 C 的列数
- m,
- // 矩阵 A 的列数,矩阵 B 的行数
- k,
- // A B 相乘的系数
- &a,
- // 矩阵 A 的显存地址
- dev_matrix_b,
- // 如果不转置,为 A 的行数即 m, 否则为 A 的列数 k
- n,
- // 矩阵 B 的显存地址
- dev_matrix_a,
- // 如果不转置,为 B 的行数即 k, 否则为 B 的列数 n
- k,
- // 运算式的 beta 值
- &b,
- // 矩阵 C,无论 A B 是否转置,都为列优先
- dev_score_vec,
- // C 的行数 m
- n);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas gemm fail: " << static_cast<int>(cublas_err);
- return -6;
- }
-
- // 同步数据
- cudaDeviceSynchronize();
-
- // 从结果从显存中取出到内存中
- cublas_err = cublasGetVector(m * n, // 要取出元素的个数
- int(float_size), // 每个元素大小
- dev_score_vec, // GPU 端起始地址
- 1, // 连续元素之间的存储间隔
- matrix_result, // 主机端起始地址
- 1 // 连续元素之间的存储间隔
- );
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas get vector fail: " << static_cast<int>(cublas_err);
- return -7;
- }
-
- // 清理显存
- cudaFree(dev_matrix_a);
- cudaFree(dev_matrix_b);
- cudaFree(dev_score_vec);
- return 0;
- }
-
- int main() {
- // 定义测试矩阵的维度
- const int m = 1;
- const int k = 4;
- const int n = 2;
- const size_t float_size = sizeof(float);
-
- // 初始化输入数据
- auto *matrix_a = (float *)malloc(m * k * float_size);
- auto *matrix_b = (float *)malloc(k * n * float_size);
- // 以列优先存储数据
- for (int i = 0; i < m * k; i++) {
- matrix_a[i] = (float)(i);
- }
- for (int i = 0; i < k * n; i++) {
- matrix_b[i] = (float)(i);
- }
-
- // 创建并初始化 CUBLAS 库对象
- cublasHandle_t handle;
- auto cublas_err = cublasCreate(&handle);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas create handle fail: " << static_cast<int>(cublas_err);
- return -1;
- }
-
- // 执行计算
- auto *matrix_result = (float *)malloc(m * n * float_size);
- auto err = CublasGEMM(matrix_result, handle, matrix_a, matrix_b, m, n, k);
- if (err != 0) {
- std::cout << "cublas gemm fail: " << err << std::endl;
- }
-
- // 打印运算结果
- std::cout << "result: " << std::endl;
- for (int i = 0; i < m * n; i++) {
- std::cout << matrix_result[i] << " ";
- if ((i + 1) % m == 0) std::cout << std::endl;
- }
-
- // 清理内存
- free(matrix_a);
- free(matrix_b);
- free(matrix_result);
-
- // 释放 CUBLAS 库对象
- cublasDestroy(handle);
- }

3.2.4 通过 cuBALS 库进行矩阵与向量的乘法
在小说业务中,主要进行的计算并非是两个矩阵之间的乘法,而是用户向量与物品向量间的乘法,所以可以直接考虑使用矩阵与向量的乘法函数 (GEMV)。
如下公式即为本例函数所实现的内容。
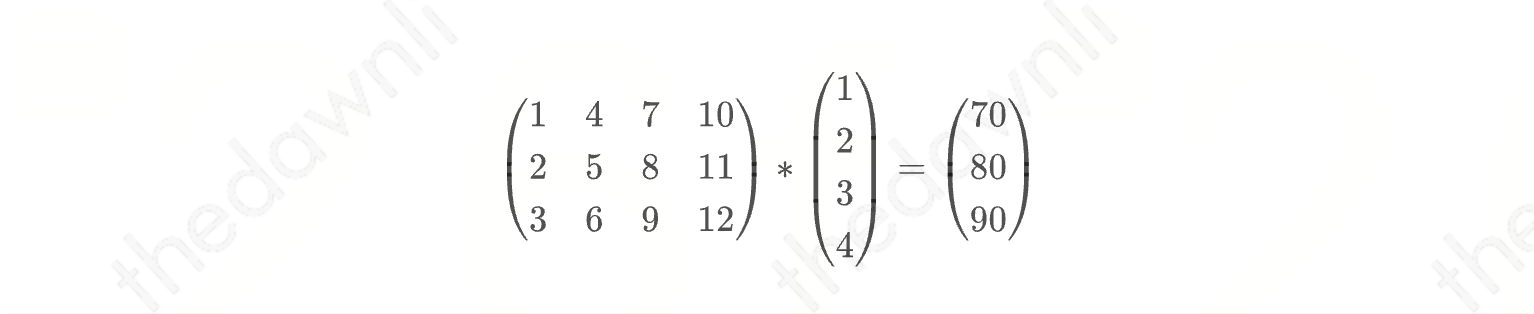
- #include <iostream>
- #include <vector>
-
- #include "cublas_v2.h"
- #include "cublas_api.h"
-
- // 执行矩阵与向量相乘
- int CublasGEMV(float *vec_result, const cublasHandle_t &handle, const float *matrix, const float *vec, int m, int n) {
- // 在 device 开辟显存
- float *dev_matrix, *dev_vec;
- size_t float_size = sizeof(float);
- auto cuda_err = cudaMalloc((void **)&dev_matrix, m * n * float_size);
- if (cuda_err != 0) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -1;
- }
- cuda_err = cudaMalloc((void **)&dev_vec, n * float_size);
- if (cuda_err != 0) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -2;
- }
-
- // 将数据拷贝到显存
- auto cublas_err = cublasSetVector(m * n, int(float_size), matrix, 1, dev_matrix, 1);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas set vector fail: " << static_cast<int>(cublas_err);
- return -3;
- }
- cublas_err = cublasSetVector(n, int(float_size), vec, 1, dev_vec, 1);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas set vector fail: " << static_cast<int>(cublas_err);
- return -4;
- }
-
- // 同步数据
- cudaDeviceSynchronize();
-
- // 为相乘结果开辟显存
- float *dev_score_vec;
- cuda_err = cudaMalloc((void **)&dev_score_vec, m * sizeof(float));
- if (cuda_err != 0) {
- std::cout << "cuda malloc fail: " << static_cast<int>(cuda_err);
- return -5;
- }
-
- // GEMV, 参数说明见 https://docs.nvidia.com/cuda/cublas/
- float a = 1;
- float b = 0;
- cublas_err = cublasSgemv(
- // cublas 库上下文句柄
- handle,
- // 矩阵 A 属性参数, 是否转置
- CUBLAS_OP_N,
- // 矩阵 A 的行数
- m,
- // 矩阵 A 的列数
- n,
- // 运算式 alpha 值
- &a,
- // 矩阵 A 的显存地址
- dev_matrix,
- // 用于存储矩阵的二维数组的前导维度(leading dimension), 通过 lda 来知道同一行中相邻两列的元素在内存中相距多远,
- // 可见其实就是数组的一列的元素个数,也就是“实际存储时的第一维”的大小。
- // 正是由于 fortran 列优先存储数组,才使得概念上的第一维(行)与实际存储时的第一维(列)不一样。
- m,
- // 向量 x 的显存中地址
- dev_vec,
- // 在 x 的连续元素之间步幅。
- 1,
- // 运算式的 beta 值
- &b,
- // 向量 y 的显存地址
- dev_score_vec,
- // 在 y 的连续元素之间步幅。
- 1);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas gemv fail: " << static_cast<int>(cublas_err);
- return -6;
- }
-
- // 同步数据
- cudaDeviceSynchronize();
-
- // 从结果从显存中取出到内存中
- cublas_err = cublasGetVector(m, // 要取出元素的个数
- sizeof(float), // 每个元素大小
- dev_score_vec, // GPU 端起始地址
- 1, // 连续元素之间的存储间隔
- vec_result, // 主机端起始地址
- 1 // 连续元素之间的存储间隔
- );
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas get vector fail: " << static_cast<int>(cublas_err);
- return -7;
- }
-
- // 清理显存
- cudaFree(dev_matrix);
- cudaFree(dev_vec);
- cudaFree(dev_score_vec);
- }
-
- int main() {
- // 初始化输入数据
- std::vector<float> matrix{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12};
- std::vector<float> vec{1, 2, 3, 4};
-
- // 创建并初始化 CUBLAS 库对象
- cublasHandle_t handle;
- auto cublas_err = cublasCreate(&handle);
- if (cublas_err != CUBLAS_STATUS_SUCCESS) {
- std::cout << "cublas create handle fail: " << static_cast<int>(cublas_err);
- return -1;
- }
-
- // 执行计算
- int m = 3;
- int n = 4;
- std::vector<float> vec_result(m);
- CublasGEMV(vec_result.data(), handle, matrix.data(), vec.data(), m, n);
-
- std::cout << "vec_result: ";
- for (int i = 0; i < m; i++) {
- std::cout << vec_result[i] << ",";
- }
- std::cout << std::endl;
-
- // 释放 CUBLAS 库对象
- cublasDestroy(handle);
- }

3.2.5 Thrust 库,获取数组的索引,并将其按其值的大小倒序排序
Thrust 是一个基于 C++ 标准模板库的 CUDA C++ 模板库,它提供了一些与 CUDA C/C++ 相互操作的高级接口,利用它可以用更少的代码开发高性能的并行应用程序。它包含多种数据并行操作功能,如扫描、排序、归约,点击这里查看更详细的文档。
本例函数实现了对于数组 , 查询器值由大到小的索引,查询结果为 。这里之所以取其索引而不是直接对数组排序,是因为我们想同时获得索引和数组值的信息。
- #include <iostream>
- #include <vector>
-
- #include <thrust/device_vector.h>
- #include <thrust/sort.h>
-
- // 获取数组的索引,并将其按其值的大小倒序排序
- std::vector<int> QueryIndexByValue(std::vector<float> &scores) {
- // 将数据复制到设备
- thrust::device_vector<float> d_data(scores.data(), scores.data() + scores.size());
- thrust::device_vector<int> d_indices(scores.size());
-
- // 初始化索引
- thrust::sequence(d_indices.begin(), d_indices.end());
-
- // 使用 Thrust 库获取按值排序的数组索引
- thrust::sort_by_key(d_data.begin(), d_data.end(), d_indices.begin(), thrust::greater<float>());
-
- // 将排序后的索引复制回主机
- thrust::host_vector<int> h_indices = d_indices;
-
- // 构造返回
- std::vector<int> indices(h_indices.begin(), h_indices.end());
- return std::move(indices);
- }
-
- int main() {
- // 定义要排序的数据
- std::vector<float> score = {1, 4, 2, 3, 5, 7};
-
- auto indices = QueryIndexByValue(score);
-
- // 打印排序后的索引
- std::cout << "Sorted indices: ";
- for (auto index : indices) {
- std::cout << index << ",";
- }
- }

与 CUDA 相关的库还有很多,这里限于篇幅就不再赘述了。


