深度学习概述_深度学习 csdn

一、 深度学习概念

深度学习(Deep Learning, DL)，由Hinton等人于2006年提出，是机器学习(MachineLearning, ML)的一个新领域

目标： 深度学习被引入机器学习使其更接近于最初的目标----人工智能（AI，Artificial Intelligence）。

实现：深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字、图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。

深度学习是一个复杂的机器学习算法，在语言和图像识别方面取得的效果，远远超过先前相关技术。它在搜索技术、数据挖掘、机器学习、机器翻译、自然语言处理、多媒体学习、语音、推荐和个性化技术，以及其它相关领域都取得了很多成果。深度学习使机器模仿视听和思考等人类的活动，解决了很多复杂的模式识别难题，使得人工智能相关技术取得了很大进步。

2006年，机器学习大师、多伦多大学教授Geoffrey Hinton及其学生Ruslan发表在世界顶级学术期刊《科学》上的一篇论文引发了深度学习在研究领域和应用领域的发展热潮。这篇文献提出了两个主要观点：

• 1.多层人工神经网络模型有很强的特征学习能力，深度学习模型学习得到的特征数据对原数据有更本质的代表性，这将大大便于分类和可视化问题；

• 2.对于深度神经网络很难训练达到最优的问题，可以采用逐层训练方法解决。将上层训练好的结果作为下层训练过程中的初始化参数。在这一文献中深度模型的训练过程中逐层初始化采用无监督学习方式。

2010年，深度学习项目首次获得来自美国国防部门DARPA计划的资助，参与方有美国NEC研究院、纽约大学和斯坦福大学。

自2011年起，谷歌和微软研究院的语音识别方向研究专家先后采用深度神经网络技术将语音识别的错误率降低20%-30%，这是长期以来语音识别研究领域取得的重大突破。2012年，深度神经网络在图像识别应用方面也获得重大进展，在ImageNet评测问题中将原来的错误率降低了9%。

同年，制药公司将深度神经网络应用于药物活性预测问题取得世界范围内最好结果。

2012年6月，Andrew NG带领的科学家们在谷歌神秘的X实验室创建了一个有16000个处理器的大规模神经网络，包含数十亿个网络节点，让这个神经网络处理大量随机选择的视频片段。经过充分的训练以后，机器系统开始学会自动识别猫的图像。这是深度学习领域最著名的案例之一，引起各界极大的关注。

深度学习本质上是构建含有多隐层的机器学习架构模型，通过大规模数据进行训练，得到大量更具代表性的特征信息。从而对样本进行分类和预测，提高分类和预测的精度。这个过程是通过深度学习模型的手段达到特征学习的目的。

深度学习模型和传统浅层学习模型的区别在于：

（1）、深度学习模型结构含有更多的层次，包含隐层节点的层数通常在5层以上，有时甚至包含多达10层以上的隐藏节点；

（2）、明确强调了特征学习对于深度模型的重要性，即通过逐层特征提取，将数据样本在原空间的特征变换到一个新的特征空间来表示初始数据，这使得分类或预测问题更加容易实现。和人工设计的特征提取方法相比，利用深度模型学习得到的数据特征对大数据的丰富内在信息更有代表性。

在统计机器学习领域，值得关注的问题是，如何对输入样本进行特征空间的选择。例如对行人检测问题，需要寻找表现人体不同特点的特征向量。

一般来说，当输入空间中的原始数据不能被直接分开时，则将其映射到一个线性可分的间接特征空间。而此间接空间通常可由3种方式获得：定义核函数映射到高维线性可分空间，如支持向量机（support vector machine，SVM）、手工编码、或自动学习。前2种方式对专业知识要求很高，且耗费大量的计算资源，不适合高维输入空间。

而第3种方式利用带多层非线性处理能力的深度学习结构进行自动学习，经实际验证被普遍认为具有重要意义与价值。

深度学习结构相对于浅层学习结构[如SVM、人工神经网络（artificial neural networks，ANN），能够用更少的参数逼近高度非线性函数。

深度学习是机器学习领域一个新的研究方向，近年来在语音识别、计算机视觉等多类应用中取得突破性的进展。其动机在于建立模型模拟人类大脑的神经连接结构，在处理图像、声音和文本这些信号时，通过多个变换阶段分层对数据特征进行描述，进而给出数据的解释。

以图像数据为例,灵长类的视觉系统中对这类信号的处理依次为：首先检测边缘、初始形状、然后再逐步形成更复杂的视觉形状，

同样地，深度学习通过组合低层特征形成更加抽象的高层表示、属性类别或特征，给出数据的分层特征表示。

深度学习之所以被称为"深度"，是相对支持向量机(supportvector machine, SVM)、提升方法(boosting)、最大熵方法等"浅层学习"方法而言的，深度学习所学得的模型中，非线性操作的层级数更多。

浅层学习依靠人工经验抽取样本特征，网络模型学习后获得的是没有层次结构的单层特征；
而深度学习通过对原始信号进行逐层特征变换，将样本在原空间的特征表示变换到新的特征空间，自动地学习得到层次化的特征表示，从而更有利于分类或特征的可视化。

深度学习理论的另外一个理论动机是：如果一个函数可用k层结构以简洁的形式表达，那么用k-1层的结构表达则可能需要指数级数量的参数(相对于输入信号)，且泛化能力不足。

深度学习算法打破了传统神经网络对层数的限制，可根据设计者需要选择网络层数。

它的训练方法与传统的神经网络相比有很大区别，传统神经网络随机设定参数初始值，采用BP算法利用梯度下降算法训练网络，直至收敛。

但深度结构训练很困难，传统对浅层有效的方法对于深度结构并无太大作用，随机初始化权值极易使目标函数收敛到局部极小值，且由于层数较多，残差向前传播会丢失严重，导致梯度扩散，因此深度学习过程中采用贪婪无监督逐层训练方法。即在一个深度学习设计中，每层被分开对待并以一种贪婪方式进行训练，当前一层训练完后，新的一层将前一层的输出作为输入并编码以用于训练；最后每层参数训练完后，在整个网络中利用有监督学习进行参数微调。

深度学习的概念 最早由多伦多大学的G. E.Hinton等于2006年提出，基于样本数据通过一定的训练方法得到包含多个层级的深度网络结构的机器学习过程。

传统的神经网络随机初始化网络中的权值，导致网络很容易收敛到局部最小值，为解决这一问题，Hinton提出使用无监督预训练方法优化网络权值的初值，再进行权值微调的方法，拉开了深度学习的序幕。

深度学习所得到的深度网络结构包含大量的单一元素(神经元)，每个神经元与大量其他神经元相连接，神经元间的连接强度(权值)在学习过程中修改并决定网络的功能。通过深度学习得到的深度网络结构符合神经网络的特征，因此深度网络就是深层次的神经网络，即深度神经网络(deep neural networks, DNN)。

深度学习的概念起源于人工神经网络的研究，有多个隐层的多层感知器是深度学习模型的一个很好的范例。

对神经网络而言，深度指的是网络学习得到的函数中非线性运算组合水平的数量。

当前神经网络的学习算法多是针对较低水平的网络结构，将这种网络称为浅结构神经网络，如一个输入层、一个隐层和一个输出层的神经网络；与此相反，将非线性运算组合水平较高的网络称为深度结构神经网络，如一个输入层、三个隐层和一个输出层的神经网络。

深度学习的基本思想：假设有系统S，它有n层（S1，…，Sn），输入为I，输出为O，可形象的表示为：I=>S1=>S2=>… =>Sn=>O。

为了使输出O尽可能的接近输入I，可以通过调整系统中的参数，这样就可以得到输入I的一系列层次特征S1，S2，…,Sn。对于堆叠的多个层，其中一层的输出作为其下一层的输入，以实现对输入数据的分级表达，这就是深度学习的基本思想。

二、 国内外研究现状

深度学习极大地促进了机器学习的发展，受到世界各国相关领域研究人员和高科技公司的重视，语音、图像和自然语言处理是深度学习算法应用最广泛的三个主要研究领域：

1、深度学习在语音识别领域研究现状

长期以来，语音识别系统大多是采用混合高斯模型(GMM)来描述每个建模单元的统计概率模型。由于这种模型估计简单，方便使用大规模数据对其训练，该模型有较好的区分度训练算法保证了该模型能够被很好的训练。在很长时间内占据了语音识别应用领域主导性地位。但是这种混合高斯模型实质上是一种浅层学习网络建模，特征的状态空间分布不能够被充分描述。而且，使用混合高斯模型建模方式数据的特征维数通常只有几十维，这使得特征之间的相关性不能被充分描述。最后混合高斯模型建模实质上是一种似然概率建模方式，即使一些模式分类之间的区分性能够通过区分度训练模拟得到，但是效果有限。

从2009年开始，微软亚洲研究院的语音识别专家们和深度学习领军人物Hinton取得合作。2011年微软公司推出了基于深度神经网络的语音识别系统，这一成果将语音识别领域已有的技术框架完全改变。采用深度神经网络后，样本数据特征间相关性信息得以充分表示，将连续的特征信息结合构成高维特征，通过高维特征样本对深度神经网络模型进行训练。由于深度神经网络采用了模拟人脑神经架构，通过逐层地进行数据特征提取，最终得到适合进行模式分类处理的理想特征。深度神经网络建模技术，在实际线上应用时，能够很好地和传统语音识别技术结合，语音识别系统识别率大幅提升。

国际上，谷歌也使用深层神经网络对声音进行建模，是最早在深度神经网络的工业化应用领域取得突破的企业之一。但谷歌的产品中使用的深度神经网络架构只有4、5层，与之相比百度使用的深度神经网络架构多达9层，正是这种结构上的差别使深度神经网络在线学习的计算难题得以更好的解决。这使得百度的线上产品能够采用更加复杂的神经网络模型。这种结构差异的核心其实是百度更好地解决了深度神经网络在线计算的技术难题，因此百度线上产品可以采用更复杂的网络模型。这对将来拓展大规模语料数据对深度神经网络模型的训练有更大的帮助。

2、深度学习在图像识别领域研究现状

对于图像的处理是深度学习算法最早尝试应用的领域。

早在1989年，加拿大多伦多大学教授Yann LeCun就和他的同事们一起提出了卷积神经网络(Convolutional Neural Networks)。卷积神经网络也称为CNN，它是一种包含卷积层的深度神经网络模型。

通常一个卷积神经网络架构包含两个可以通过训练产生的非线性卷积层，两个固定的子采样层和一个全连接层，隐藏层的数量一般至少在5个以上。

CNN的架构设计是受到生物学家Hubel和Wiesel的动物视觉模型启发而发明的，尤其是模拟动物视觉皮层V1层和V2层中简单细胞(Simple Cell)和复杂细胞(Complex Cell)在视觉系统的功能。

起初卷积神经网络在小规模的应用问题上取得了当时世界最好成果。但在很长一段时间里一直没有取得重大突破。主要原因是由于卷积神经网络应用在大尺寸图像上一直不能取得理想结果，比如对于像素数很大的自然图像内容的理解，这使得它没有引起计算机视觉研究领域足够的重视。

直到2012年10月，Hinton教授以及他的两个学生采用更深的卷积神经网络模型在著名的ImageNet问题上取得了世界最好成果，使得对于图像识别的研究工作前进了一大步。Hinton构建的深度神经网络模型是使用原始的自然图像训练的，没有使用任何人工特征提取方法。

自卷积神经网络提出以来，在图像识别问题上并没有取得质的提升和突破，直到2012年Hinton构建的深度神经网络才取得惊人成果。这主要是因为对算法的改进，在网络的训练中引入了权重衰减的概念，有效的减小权重幅度，防止网络过拟合。更关键的是计算机计算能力的提升，GPU加速技术的发展，这使得在训练过程中可以产生更多的训练数据，使网络能够更好的拟合训练样本。

2012年国内互联网巨头百度公司将相关最新技术成功应用到人脸识别和自然图像识别问题，并推出了相应的产品。现在深度学习网络模型已能够理解和识别一般的自然图像。深度学习模型不仅大幅提高了图像识别的精度，同时也避免了需要消耗大量的时间进行人工特征提取的工作，使得在线运算效率大大提升。深度学习将有可能取代以往人工和机器学习相结合的方式成为主流图像识别技术。

3、深度学习在自然语言处理领域研究现状

自然语言处理(NLP)问题是深度学习在除了语音和图像处理之外的另一个重要应用领域。

数十年以来，自然语言处理的主流方法是基于统计的模型，人工神经网络也是基于统计方法模型之一，但在自然语言处理领域却一直没有被重视。语言建模是最早采用神经网络进行自然语言处理的问题。

美国的NEC研究院最早将深度学习引入到自然语言处理研究工作中，其研究人员从2008年起采用将词汇映射到一维矢量空间方法和多层一维卷积结构去解决词性标注、分词、命名实体识别和语义角色标注四个典型的自然语言处理问题。他们构建了同一个网络模型用于解决四个不同问题，都取得了相当精确的结果。总体而言，深度学习在自然语言处理问题上取得的成果和在图像语音识别方面还有相当的差距，仍有待深入探索。

由于深度学习能够很好地解决一些复杂问题，近年来许多研究人员对其进行了深人研究，出现了许多有关深度学习研究的新进展。

下面分别从初始化方法、网络层数和激活函数的选择、模型结构两个个方面对近几年深度学习研究的新进展进行介绍。

1、 初始化方法、网络层数和激活函数的选择

研究人员试图搞清网络初始值的设定与学习结果之间的关系。 Erhan等人在轨迹可视化研究中指出即使从相近的值开始训练深度结构神经网络，不同的初始值也会学习到不同的局部极值，同时发现用无监督预训练初始化模型的参数学习得到的极值与随机初始化学习得到的极值差异比较大，用无监督预训练初始化模型的参数学习得到的模型具有更好的泛化误差。Bengio与Krueger等人指出用特定的方法设定训练样例的初始分布和排列顺序可以产生更好的训练结果，用特定的方法初始化参数，使其与均匀采样得到的参数不同，会对梯度下降算法训练的结果产生很大的影响。Glorot等人指出通过设定一组初始权值使得每一层深度结构神经网络的Jacobian矩阵(描述了一个向量值函数的每个输出分量相对于每个输入分量的变化率的矩阵)的奇异值接近1，在很大程度上减小了监督深度结构神经网络和有预训练过程设定初值的深度结构神经网络之间的学习结果差异。另外，用于深度学习的学习算法通常包含许多超参数，一些常用的超参数（超参数是在训练模型之前设置的参数，而不是通过训练数据来学习的参数。），尤其适用于基于反向传播的学习算法和基于梯度的优化算法。

参数初始化

深度学习的参数初始化的原理是为了使得模型在训练过程中更容易收敛到最优解。在深度学习中，模型的参数通常是通过随机初始化来得到的。如果参数的初始值过大或过小，都会导致模型的训练变得困难，甚至无法收敛。因此，参数初始化方法的目的是将参数初始化为一个适当的范围，使得模型在训练过程中更容易收敛。
常用的参数初始化方法包括 Xavier 初始化和 He 初始化。Xavier 初始化是根据输入和输出的维度来进行参数初始化的方法，可以使得每一层的输出方差相等。而 He 初始化则是针对 ReLU 激活函数的初始化方法，可以避免梯度消失问题。
需要注意的是，不同的模型和任务可能需要不同的参数初始化方法，因此在实际应用中需要根据具体情况选择合适的初始化方法。

硬核版本：

基于梯度的优化算法

基于梯度的优化算法: 梯度是指一个向量，它指向函数在某一点处增加最快的方向。在机器学习和优化领域，基于梯度的方法被广泛应用于求解函数的最小值或最大值。这些方法通过计算函数在当前点处的梯度，并沿着梯度的反方向更新当前点的位置，以逐步接近函数的最小值或最大值。常见的基于梯度的方法包括梯度下降、共轭梯度等。

用一个直线来拟合这三个点，直线方程是y=wx+b，假设斜率w已知想要找到一个最合适的b。

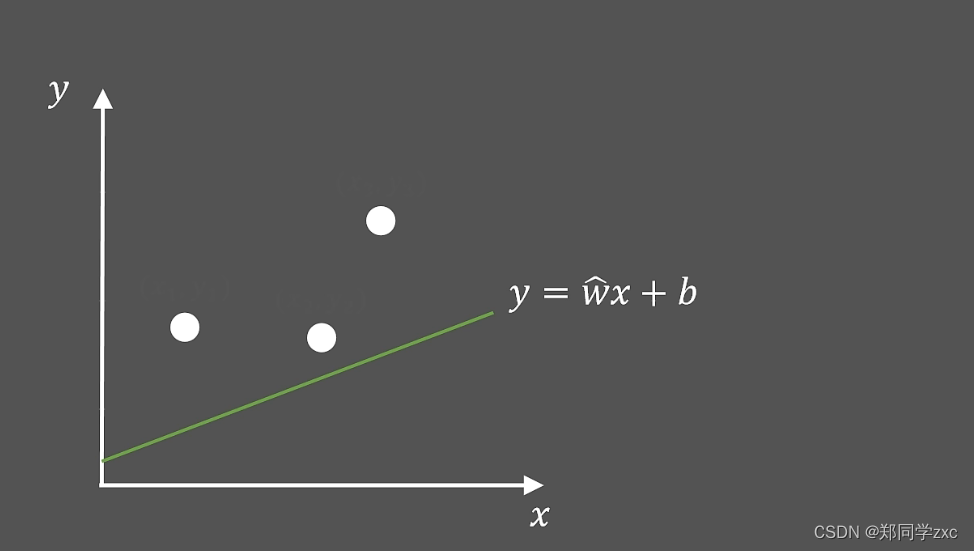
判定直线方程好坏标准：三个点到直线的距离来衡量，然后将距离的写成一个最小二乘的方程，即损失函数

目标：找到解决b，让损失函数最小。将直线方程带入到损失函数中得到如下方程，损失函数是关于b的一个二次函数。其他系数可以计算出来。二次函数找最小的b值很容易

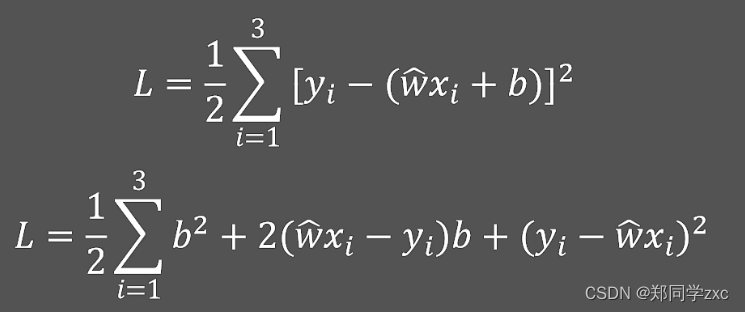
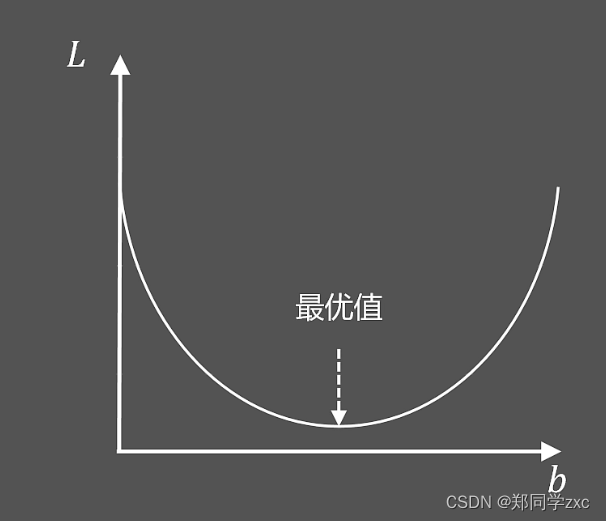
梯度下降算法：就是随便给出b的值经过迭代优化的方式找到最好的值
求出初始状态下的斜率的绝对值|dL/db|然后乘以一个常数 ε (epsilon),然后去更新b的值。
b= b - ε *（dL/db）。单个点的（dL/db）就是梯度值，需要计算出所有梯度然后取平均值g =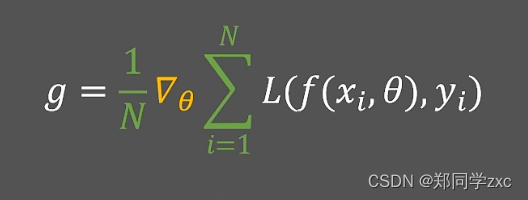
，ε就是学习率，人为设定，来控制梯度下降步长。

按照这个思路当点越来越多时需要计算出所有点的梯度，保存下来，内存开销大，然后取平均值，速度较慢。

改进：随机取值（类似于等比抽样）求梯度取平均，随机梯度下降算法。并非所有情况都有效。

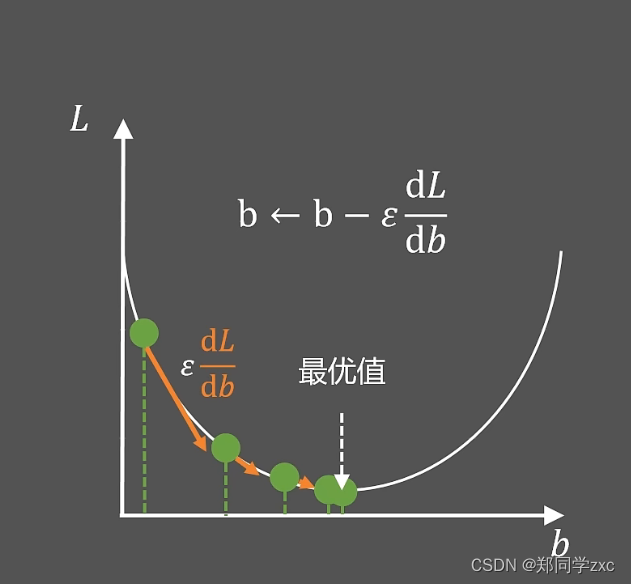
为了让学习率 ε 自动变化，引入变量r，r时梯度大小随时间的积累量的变化率，用学习率 ε除以r，再来乘以梯度。

总结：

那么同理w的值也能使用同样的思路来找到一个合适的值

反向传播: 这个算法主要用于神经网络模型中的权重更新，以便最小化预测误差。在反向传播算法中，误差被反向传递回神经网络中，以便调整每个权重的值。这个算法使用链式法则来计算误差对于每个权重的影响，从而更新它们的值。
继续使用线性拟合的例子。
用最小二乘法表达损失函数，其中ygt是真实值，假设w=0.8，b=0.2。x=1.5得到y=1.4,但是此时真实值是0.8,则损失函数值为0.18。如何来调整w,b呢？

根据梯度下降算法计算损失函数L对于w和b的梯度值，即偏导数，然后再沿着梯度的反方向更新两个参数。
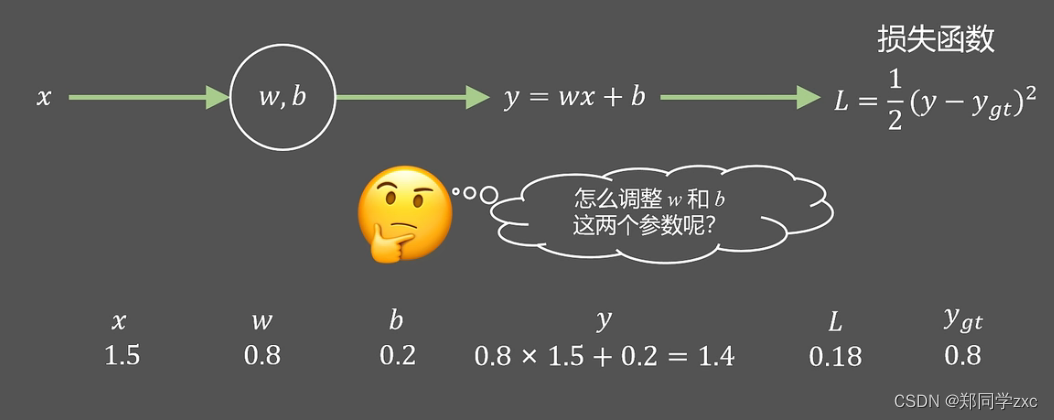为了更容易计算损失函数L对于w,b的偏导，最好先计算一个中间量就是损失函数L对y的偏导这样L对w的偏导就可以写成L对y的偏导乘以y对w的偏导（即求到的链式法则）同时也可以计算出L对b的偏导,通过这种反向从后向前的方式得到参数梯度的解析式

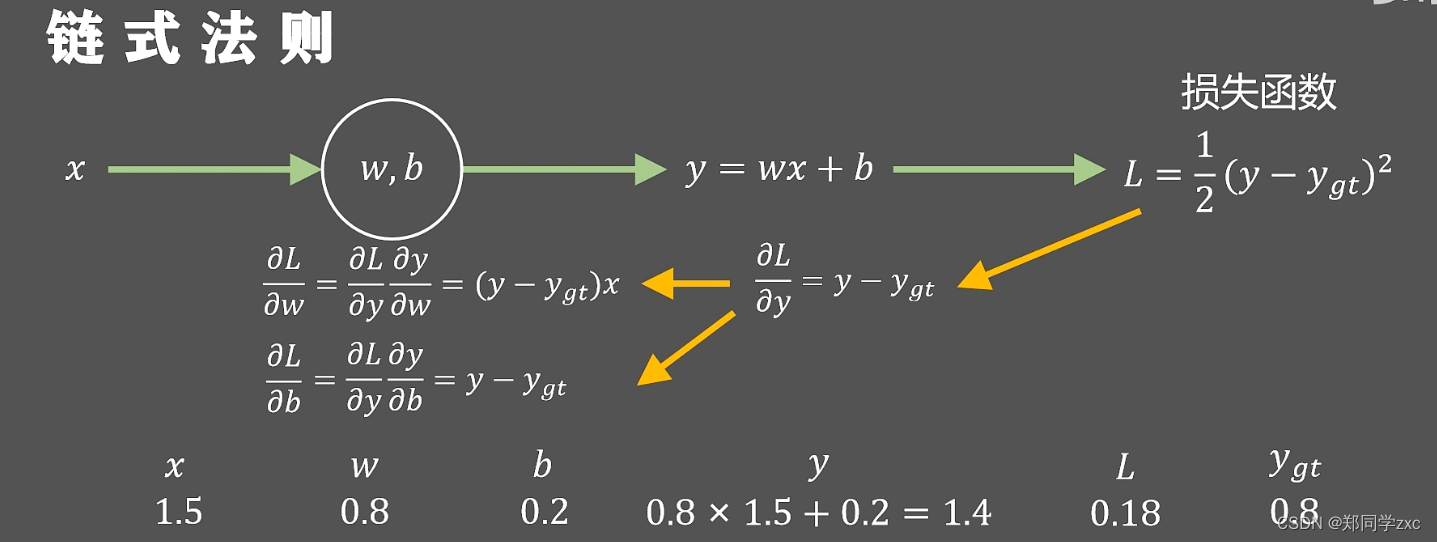
这种沿着黄色箭头从后向前计算梯度值的方法就是方向传播算法

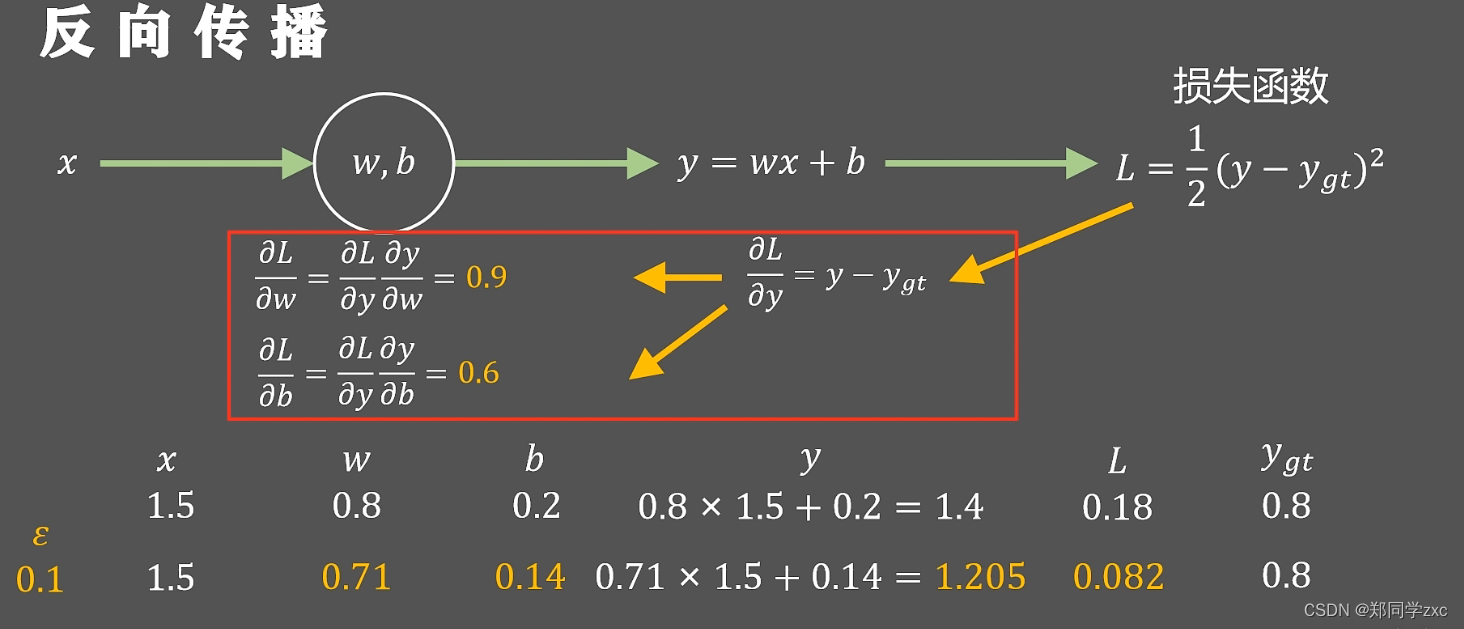
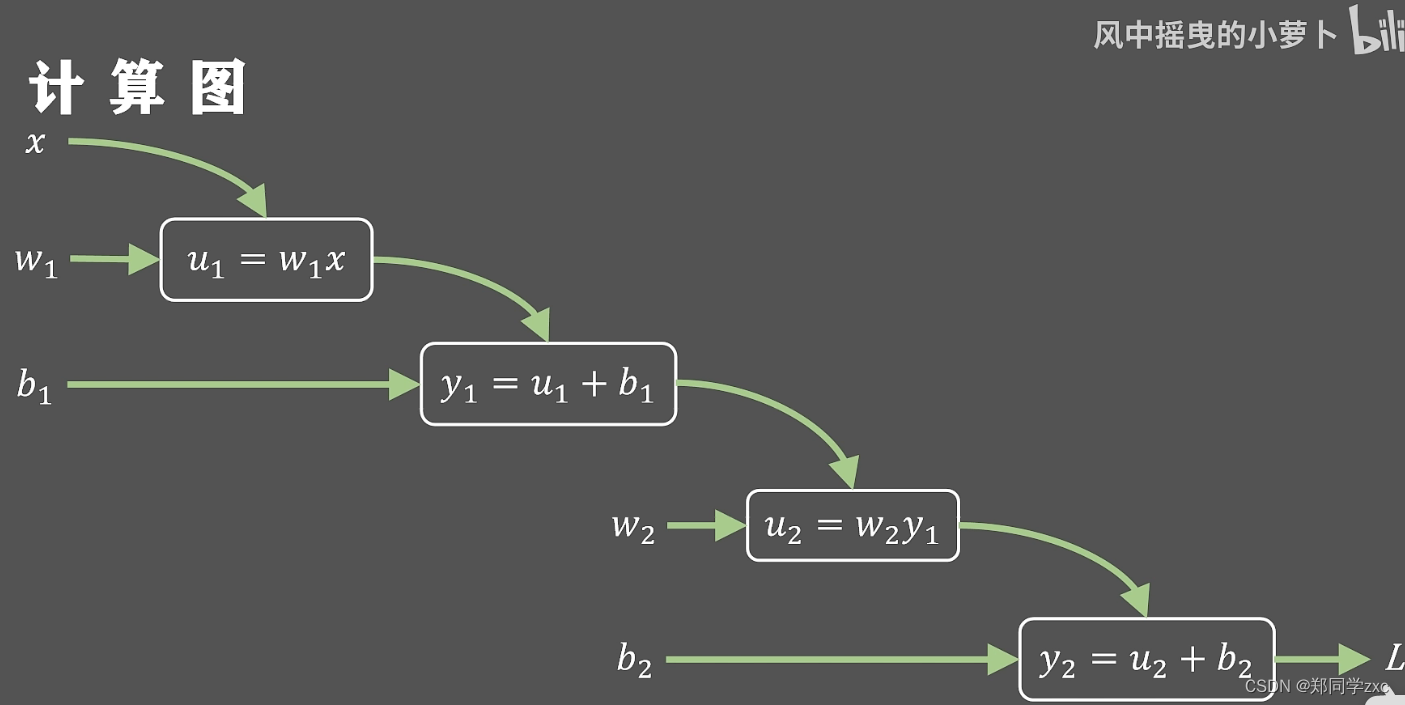
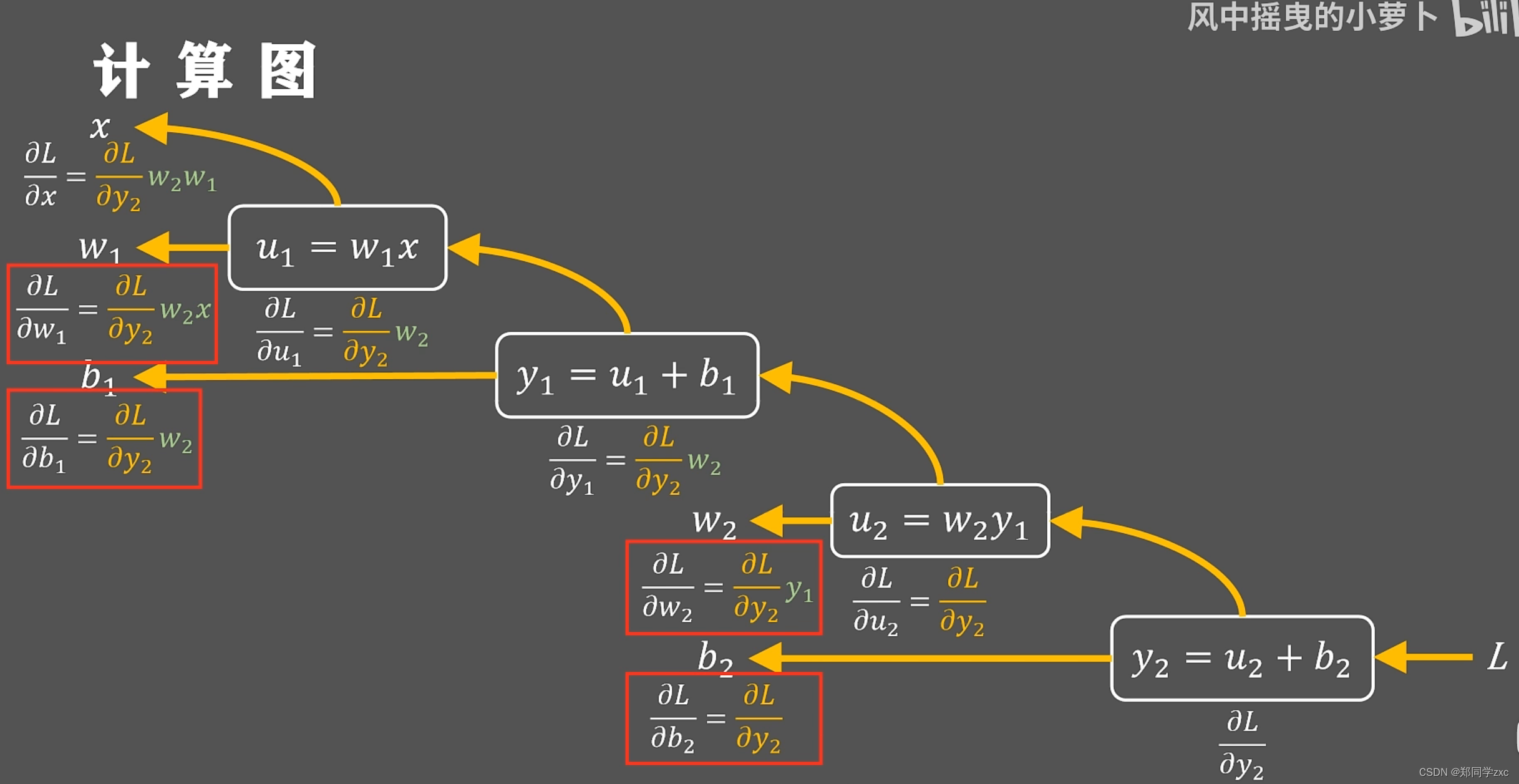
在深度学习框架中所有单元都有定义的向前传播和反向传播函数这样就可以；利用方向传播算法来更新亿万的网络参数

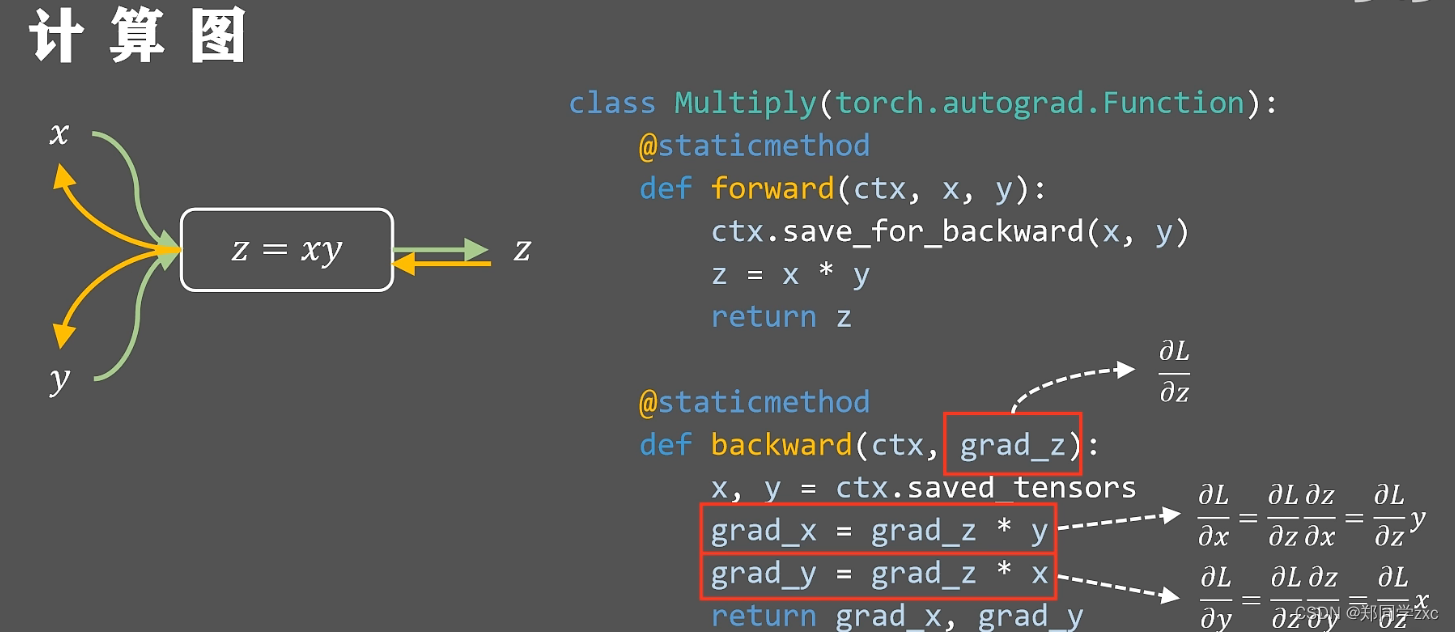
总结：

选择不同的网络隐层数和不同的非线性激活函数会对学习结果产生不同的影响。 Glorot等人研究了隐层非线性映射关系的选择和网络的深度相互影响的问题，讨论了随机初始化的标准梯度下降算法用于深度结构神经网络学习得到不好的学习性能的原因。Glorot等人观察不同非线性激活函数对学习结果的影响，得到逻辑斯蒂S型激活单元的均值会驱使顶层和隐层进入饱和，因而逻辑斯蒂S型激活单元不适合用随机初始化梯度算法学习深度结构神经网络；并据此提出了标准梯度下降算法的一种新的初始化方案来得到更快的收敛速度。Bengio等人从理论上说明深度学习结构的表示能力随着神经网络深度的增加以指数的形式增加，但是这种增加的额外表示能力会引起相应局部极值数量的增加，使得在其中寻找最优值变得困难。

激活函数: 激活函数是一种函数，它接收神经元的输入并产生输出。在神经网络中，激活函数通常用于非线性转换，以便神经网络可以学习非线性关系。常见的激活函数包括sigmoid、ReLU、tanh等。

给出一个线性变换函数y1=w1x+b1，可以吧x的值映射到一条直线上，在进行嵌套一次给出关于y1线性变换函数y2=w2y1+b2;那么x与y2的关系也是线性的y2=（w1w2）x+w2b1+b2。以此类推有许多层线性变换到最终yn=(w1w2…wn)x + wn b(n-1) … + bn,yn与x永远都是线性的。最终只能解决线性问题。 怎么解决非线性问题，加入一个非线性函数

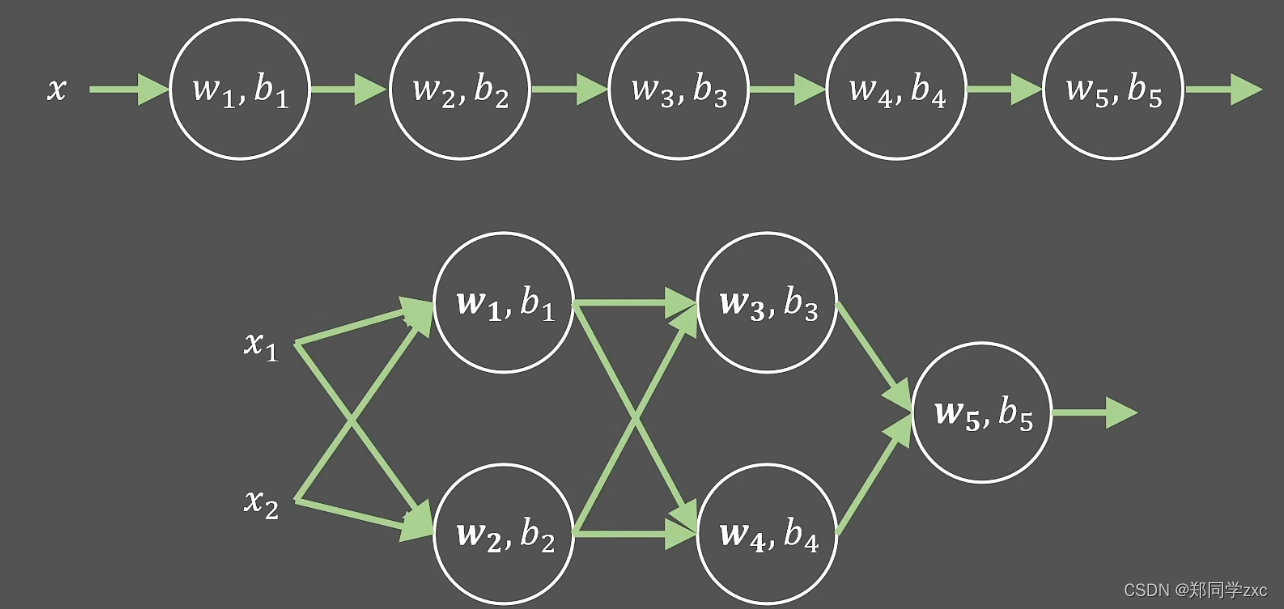
类似于神经元的激活，将这个非线性函数叫做激活函数

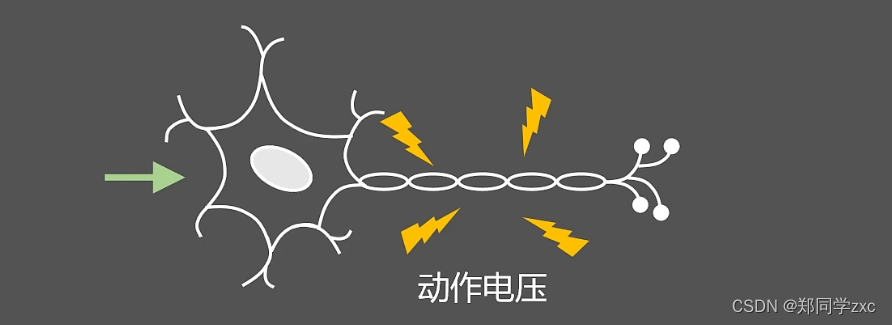
激活函数的条件：
通过反向传播在更新w,b的过程中，需要知道o对y的偏导数即f的倒数，所以激活函数f必须也是连续可导的。另外为了数值的稳定性所以激活函数要映射所有实数，定义域一定是所有实数R 。并且激活函数只是增加非线性并不改变输入的响应状态，即与输入的趋势相同，所以一定是单调递增的，但是又要保证一定的非线性所以就是一个单调的S型曲线。

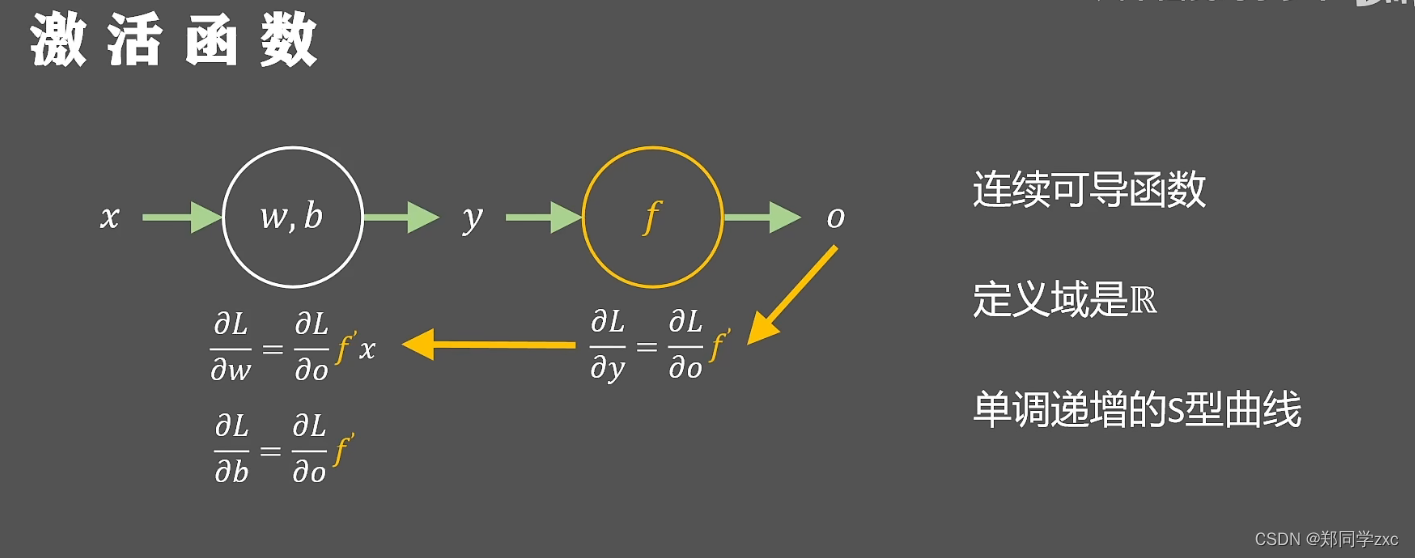
研究者首先想到的是sigmoid函数，非线性函数值域（0，1）。

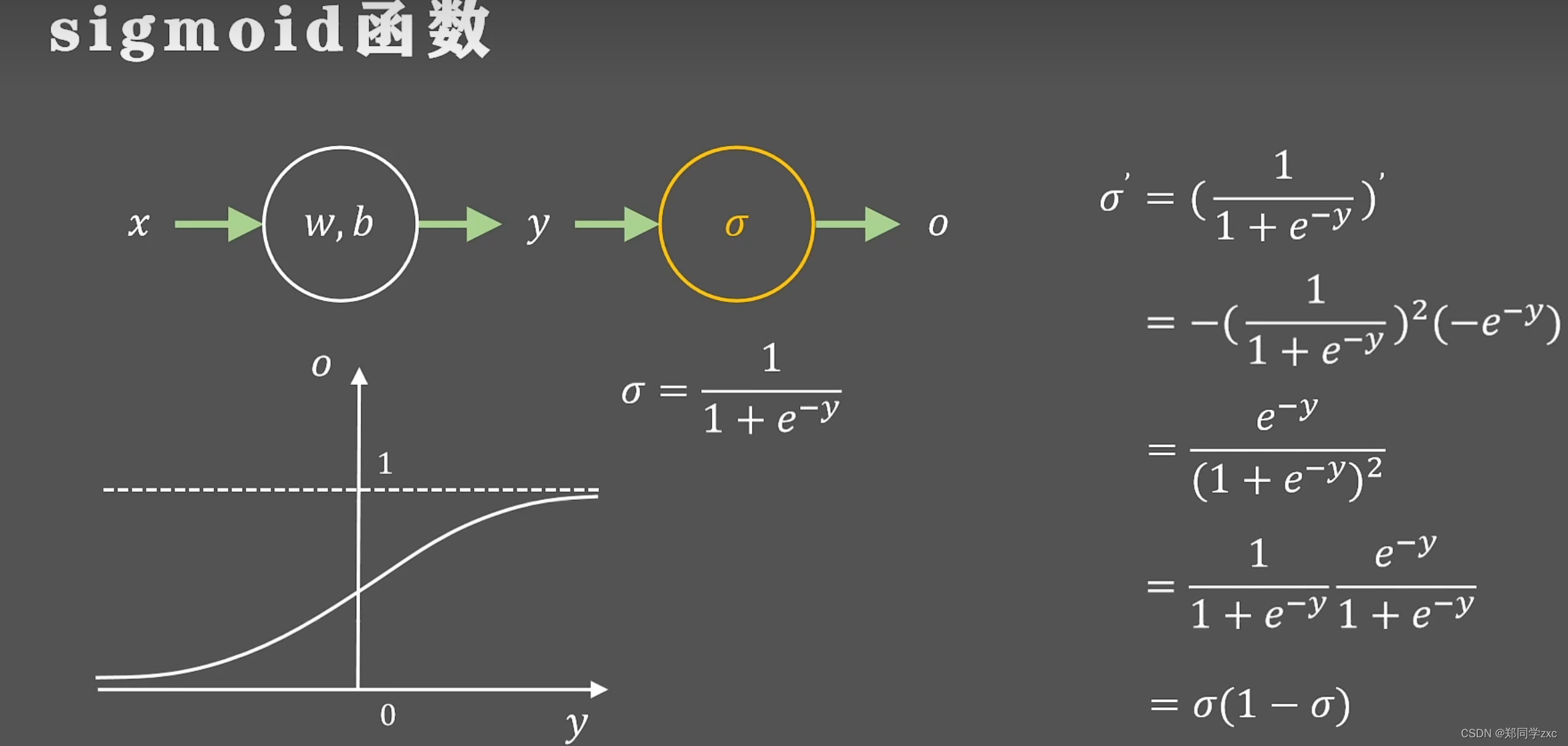
sigmoid函数的导数就是关于y的钟型图形最大值是0.25。 当y很大或者很小时导数值为0。 在正负无穷处梯度为0的函数叫做饱和函数，无论如何取值导数最大值是0.25，这就意味着神经网络在反向传播时，分层梯度会被动的缩小大约0.25 ，当网络层数较多时或者某层出现极端的输出反向传播的链式法则，导致前几层的梯度几乎为0，参数不会消失，层数失去作用，这就是梯度消失现象

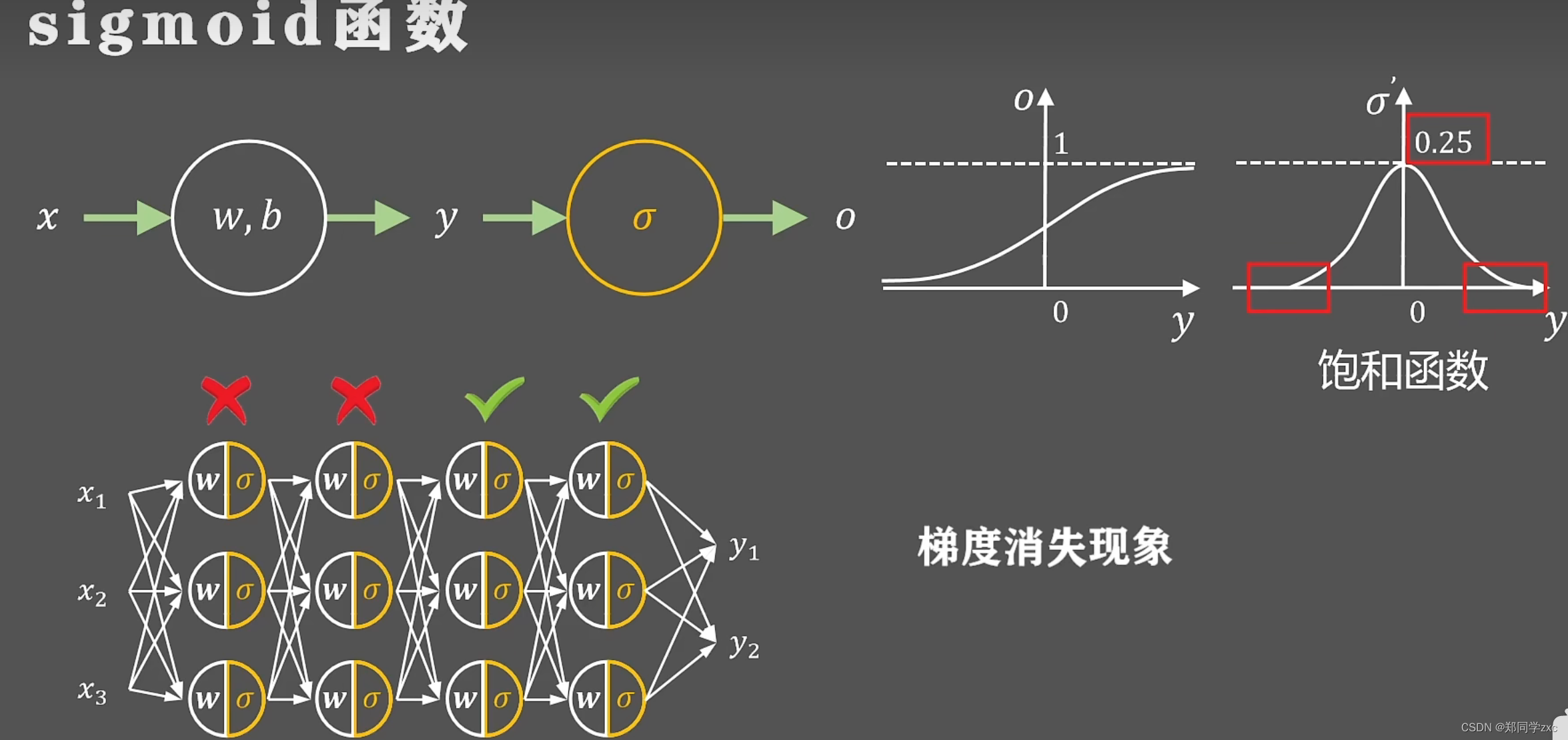
。除此之外sigmoid函数的取值是（0，1） ,都大于0，叫做非零均值函数。 当一个神经元的输入是x1 ,x2，是上一层sigmoid函数的输出所以都大于0。进行反向传播后得到
w1 w2的梯度，黄色字体的式子始终大于0 ，这两个参数的梯度正负性取决于损失函数L对o的导数，随意w1w2的梯度符号始终一致，强制的同时向一个方向更新，会导致神经网络更慢的收敛 。

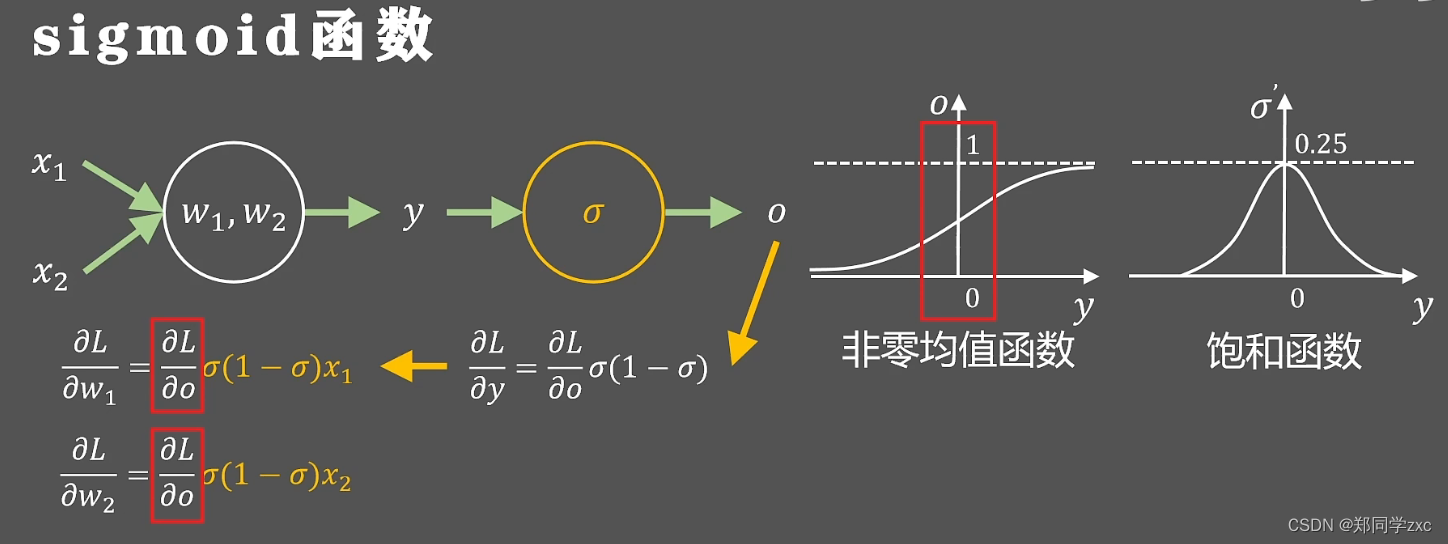
综上所述sigmoid函数会导致梯度消失和不易收敛问题

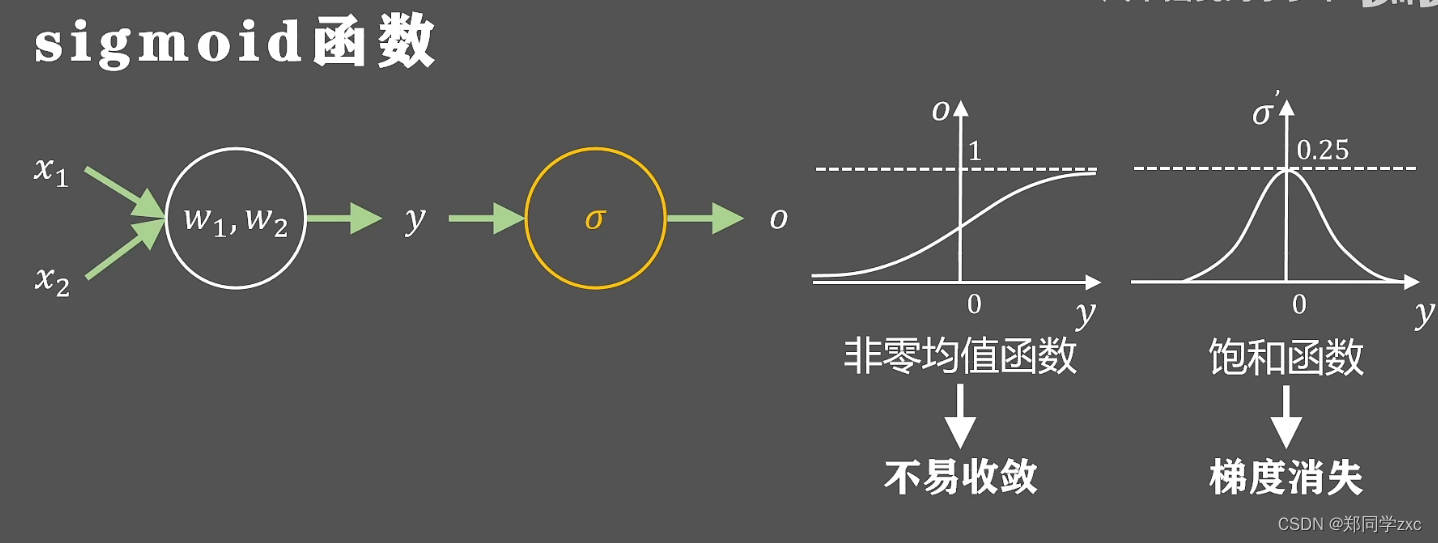
为了解决上述问题引入了双曲正切函数tanh，在坐标轴中的图像以及导数图像如下：值域（-1，1），定义域R，零均值函数性能会由于sigmoid函数，但是也是一个饱和函数会导致梯度消失现象

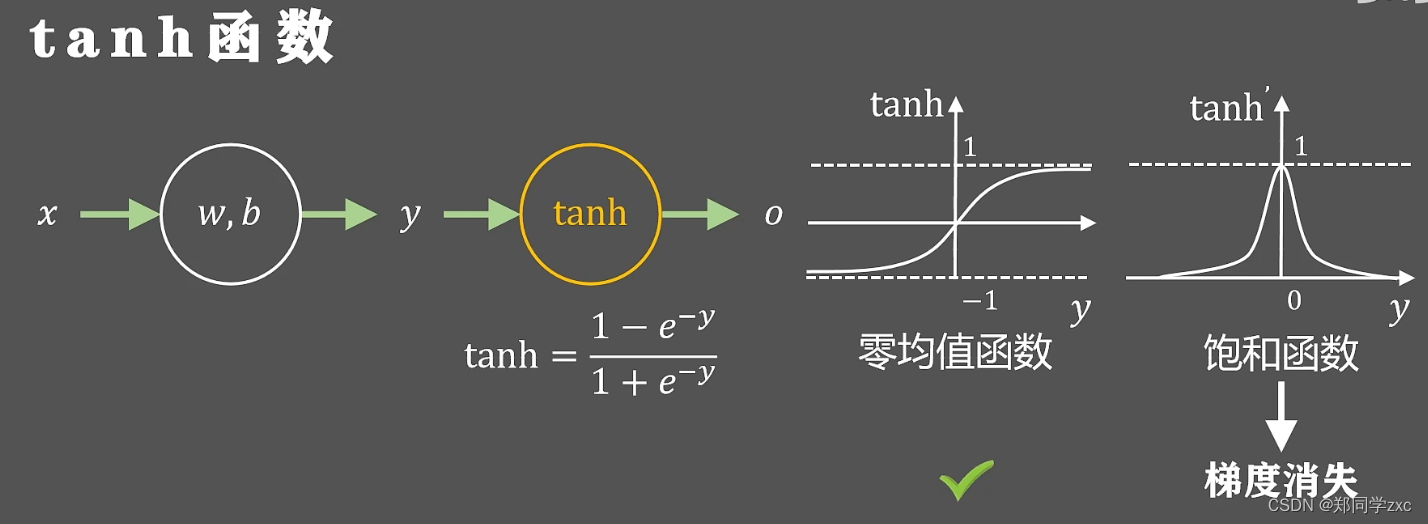
修正线性单元函数， 导数图像如下，只有当神经元的输出大于0的时候才会回传梯度 ，小于0则不会反向传播。非零均值函数， 非饱和函数。在训练过程中可以动态控制神经元的状态要么激活大于0 ，要么等于0被抑制，稀疏性。
如果输入的参数发生了一个很小的改动只需要少部分神经元改变状态，不需要全局调整，信息的耦合程度降低 。动态开启关闭神经元的做法 可以支持不同输入维度和中间层维度的学习，这种稀疏的表达方式一般是线性可分或者弱线性可分的，可以降低网络训练的难度，虽然输出的特征是稀疏的但是被激活的输出保持着原有的表达能力。

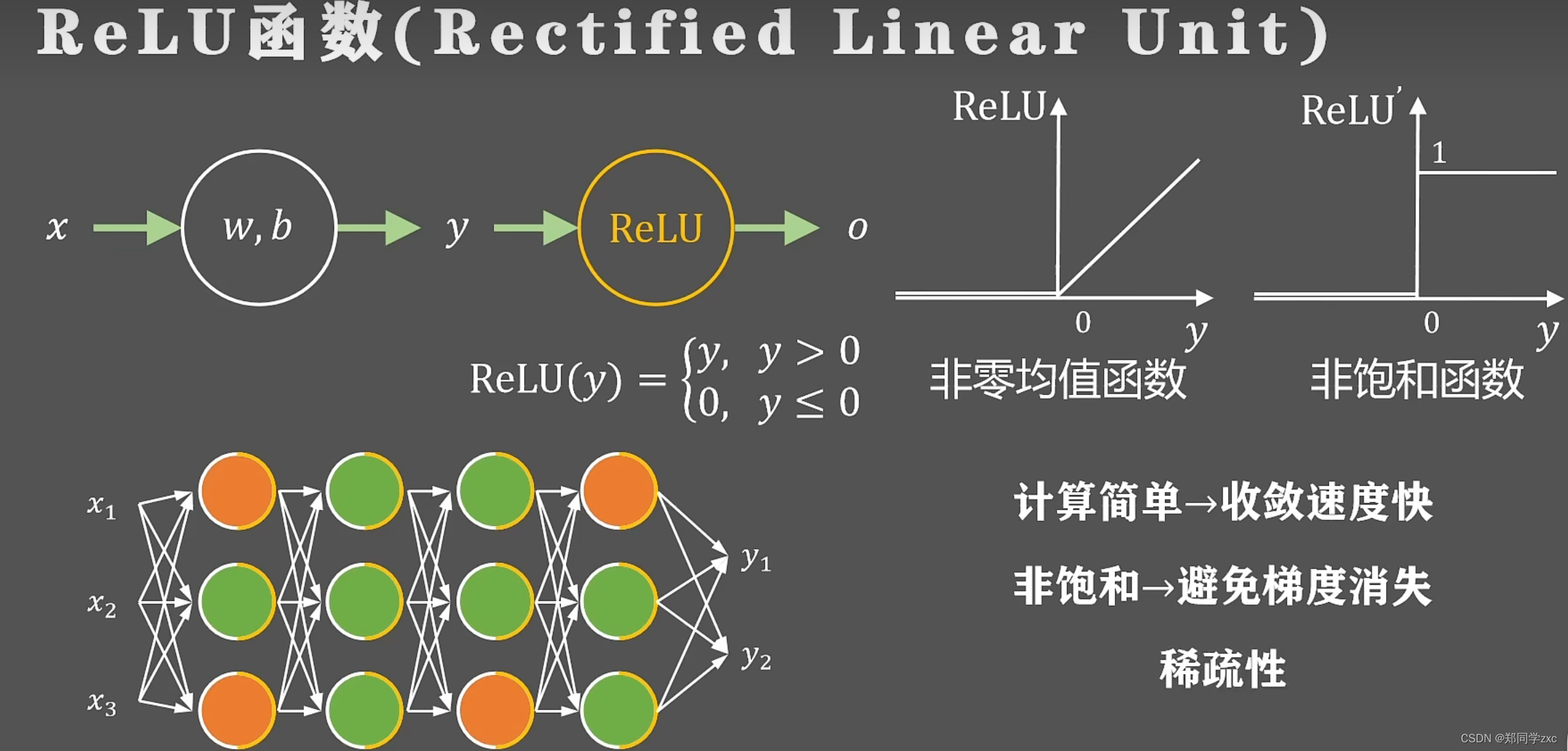
稀疏性=》信息耦合程度低，表达维度尺寸可变，稀疏表达线性可分，保持特征的表达能力

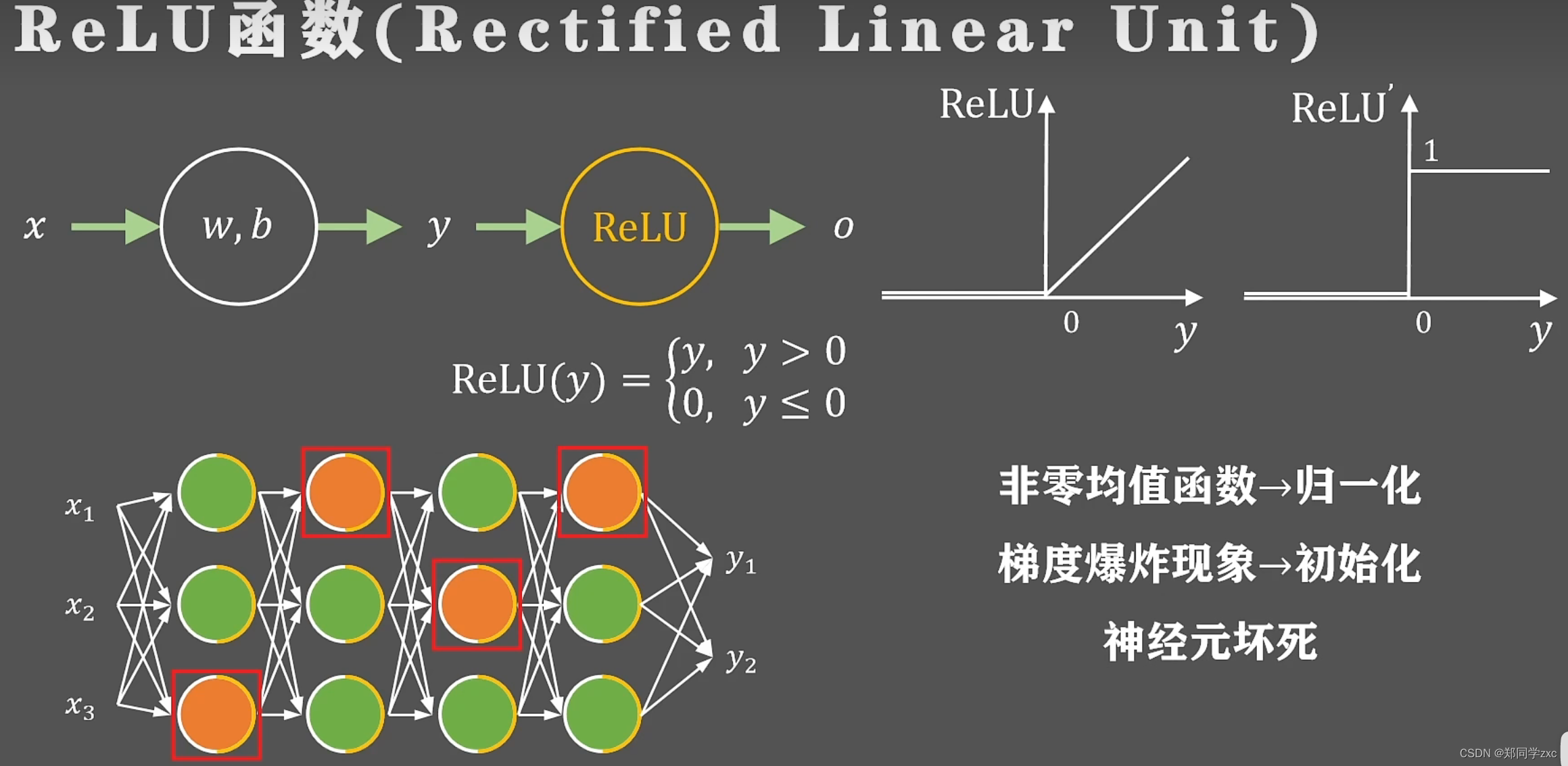
问题：非零均值函数造成不易收敛，可以通过归一化解决
输出没有上界如果闲心单元输出过大或者网络是循环结构会导致梯度累积超出计算机计算上限，这种叫做梯度爆炸现象需要重新设计网络结构和参数初始化来解决

在训练过程中一些神经元始终不会被激活 ，导致网络表达能力下降问题这种现象是神经元坏死现象

在2013年提出了下面函数避免神经元函数坏死

2015年提出下列函数将负半轴的梯度值更换成可以学习的参数是否保持稀疏性和抑制神经元都要通过训练过程来确定

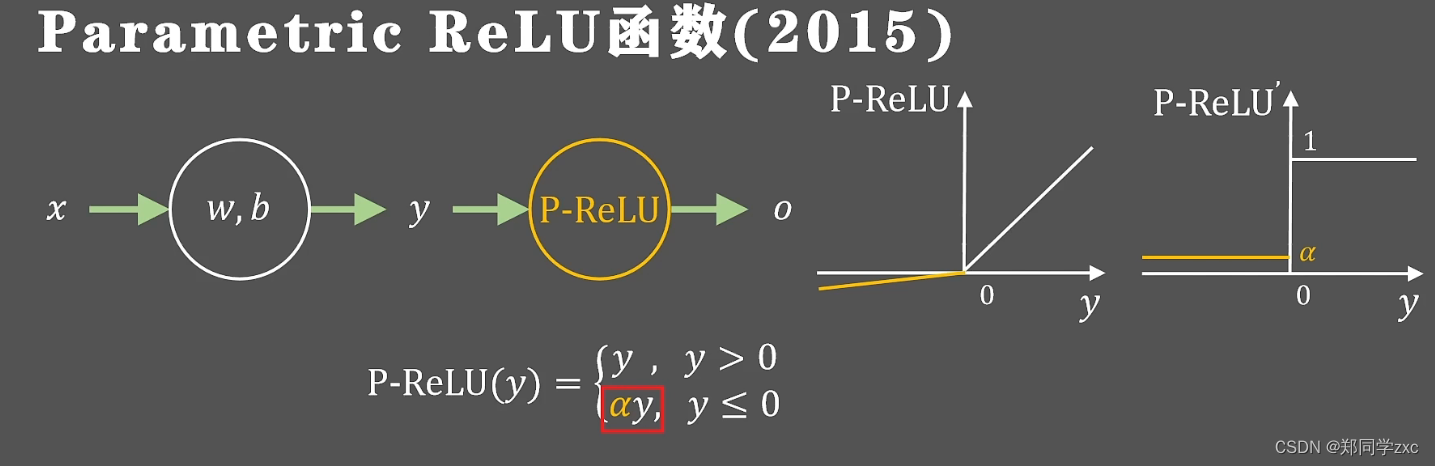
总结：

2、 模型结构

(1)、DBN的结构及其变种： 采用二值可见单元和隐单元RBM作为结构单元的DBN，在MNIST等数据集上表现出很好的性能。近几年，具有连续值单元的RBM，如mcRBM、mPoT(“Multi-Perspective Object Tracking”（多角度目标跟踪）)模型和spike—and-slab RBM等已经成功应用。Spike—and—slab RBM中spike表示以0为中心的离散概率分布，slab表示在连续域上的稠密均匀分布，可以用吉布斯采样对spike—and—slab RBM进行有效推断，得到优越的学习性能。

DBN: 是一种深度信念网络（Deep Belief Network）的缩写。它是一种由多个隐层组成的前馈神经网络，通常用于无监督学习任务，例如特征提取和数据降维。DBN的基本单元是受限玻尔兹曼机（Restricted Boltzmann Machine，RBM），多个RBM可以组成一个DBN。

RBM: 是受限玻尔兹曼机（Restricted Boltzmann Machine）的缩写。它是一种用于无监督学习的神经网络模型，通常用于特征提取和数据降维。RBM由一个可见层和一个隐层组成，其中可见层和隐层之间的连接是无向的，并且节点之间没有连接。在训练过程中，RBM会自动学习输入数据中的特征，并将其编码为一组隐藏的特征表示。RBM使用马尔可夫链蒙特卡罗（Markov Chain Monte Carlo，MCMC）算法进行训练，其中包括对比散度（Contrastive Divergence）等技术。

MNIST: 是一个手写数字数据集，包含60,000个训练图像和10,000个测试图像。这些图像都是28x28像素的灰度图像，表示0到9之间的数字。MNIST数据集通常用于测试图像分类算法的性能。在机器学习中，MNIST数据集被广泛用于训练和测试各种分类算法，如神经网络、支持向量机和决策树等。

(2)、和–积网络； 深度学习最主要的困难是配分函数的学习，如何选择深度结构神经网络的结构使得配分函数更容易计算? Poon等人提出一种新的深度模型结构----和–积网络(sum—product network，SPN)，引入多层隐单元表示配分函数，使得配分函数更容易计算SPN是一种概率图模型，用于表示概率分布。它由一些基本的节点组成，包括和节点和积节点。和节点计算其子节点的和，而积节点计算其子节点的乘积。SPN可以用于许多机器学习任务，例如分类、回归和密度估计。连接节点的边带有权值，它们在Caltech-101和Olivetti两个数据集上进行实验证明了SPN的性能优于DBN和最近邻方法。

配分函数: 是用于计算概率分布中所有可能状态的总和，它在很多机器学习模型中都扮演着重要的角色。然而，计算配分函数通常是一个复杂且耗时的过程，特别是在深度学习中，这一问题变得更加严重。因此，研究人员一直在寻找新的方法来解决这个问题，例如使用Monte Carlo方法或近似算法来估计配分函数。

(3)、基于rectified单元的学习： Glorot与Mesnil等人用降噪自编码模型来处理高维输入数据。与通常的S型和正切非线性隐单元相比，该自编码模型使用rectified单元，使隐单元产生更加稀疏的表示。对于高维稀疏数据，Dauphin等人采用抽样重构算法，训练过程只需要计算随机选择的很小的样本子集的重构和重构误差，在很大程度上提高了学习速度，实验结果显示提速了20倍。Glorot等人提出在深度结构神经网络中，在图像分类和情感分类问题中用rectified非线性神经元代替双曲正切或S型神经元，指出rectified神经元网络在零点产生与双曲正切神经元网络相当或者有更好的性能，能够产生有真正零点的稀疏表示，非常适合本质稀疏数据的建模，在理解训练纯粹深度监督神经网络的困难，搞清使用或不使用无监督预训练学习的神经网络造成的性能差异方面，可以看做新的里程碑；Glorot等人还提出用增加L1正则化项来促进模型稀疏性，使用无穷大的激活函数防止算法运行过程中可能引起的数值问题。在此之前，Nair等人提出在RBM环境中rectifed神经元产生的效果比逻辑斯蒂S型激活单元好，他们用无限数量的权值相同但是负偏差变大的一组单元替换二值单元，生成用于RBM的更好的一类隐单元，将RBM泛化，可以用噪声rectified线性单元(rectified linear units)有效近似这些S型单元。用这些单元组成的RBM在NORB数据集上进行目标识别以及在数据集上进行已标记人脸实际验证，得到比二值单元更好的性能，并且可以更好地解决大规模像素强度值变化很大的问题。

自编码: 是一种无监督学习算法，它可以从输入数据中学习到一种压缩表示，并用这种表示来重建输入数据。降噪自编码模型是一种特殊的自编码模型，它在训练过程中会向输入数据中添加噪声，以提高模型的鲁棒性和泛化能力。这种模型在图像处理、语音识别、自然语言处理等领域有广泛的应用。

rectified单元: 它是一种在神经网络中经常使用的激活函数。激活函数是神经网络中的一种数学函数，它将输入转换为输出，并在整个网络中传递信号。Rectified Linear Unit(ReLU)是一种非线性激活函数，它在输入为负数时输出为0，而在输入为正数时输出等于输入本身。这使得ReLU比其他激活函数更容易优化和计算，并且在许多深度学习应用中表现出色。

(4)、卷积神经网络： 研究了用生成式子抽样单元组成的卷积神经网络，在MNIST数字识别任务和Cahech一101目标分类基准任务上进行实验，显示出非常好的学习性能。Huang等人提出一种新的卷积学习模型----局部卷积RBM，利用对象类中的总体结构学习特征，不假定图像具有平稳特征，在实际人脸数据集上进行实验，得到性能很好的实验结果.

三个典型的局部特征：

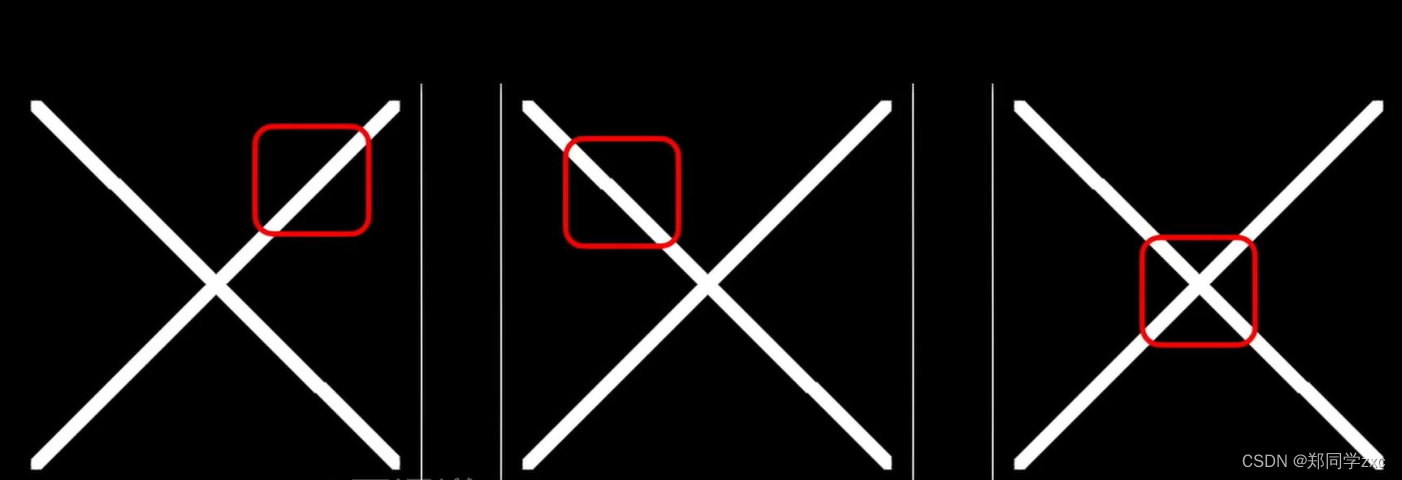
将原始的图像矩阵化，

分别制造三个特征的小矩阵（卷积核）：

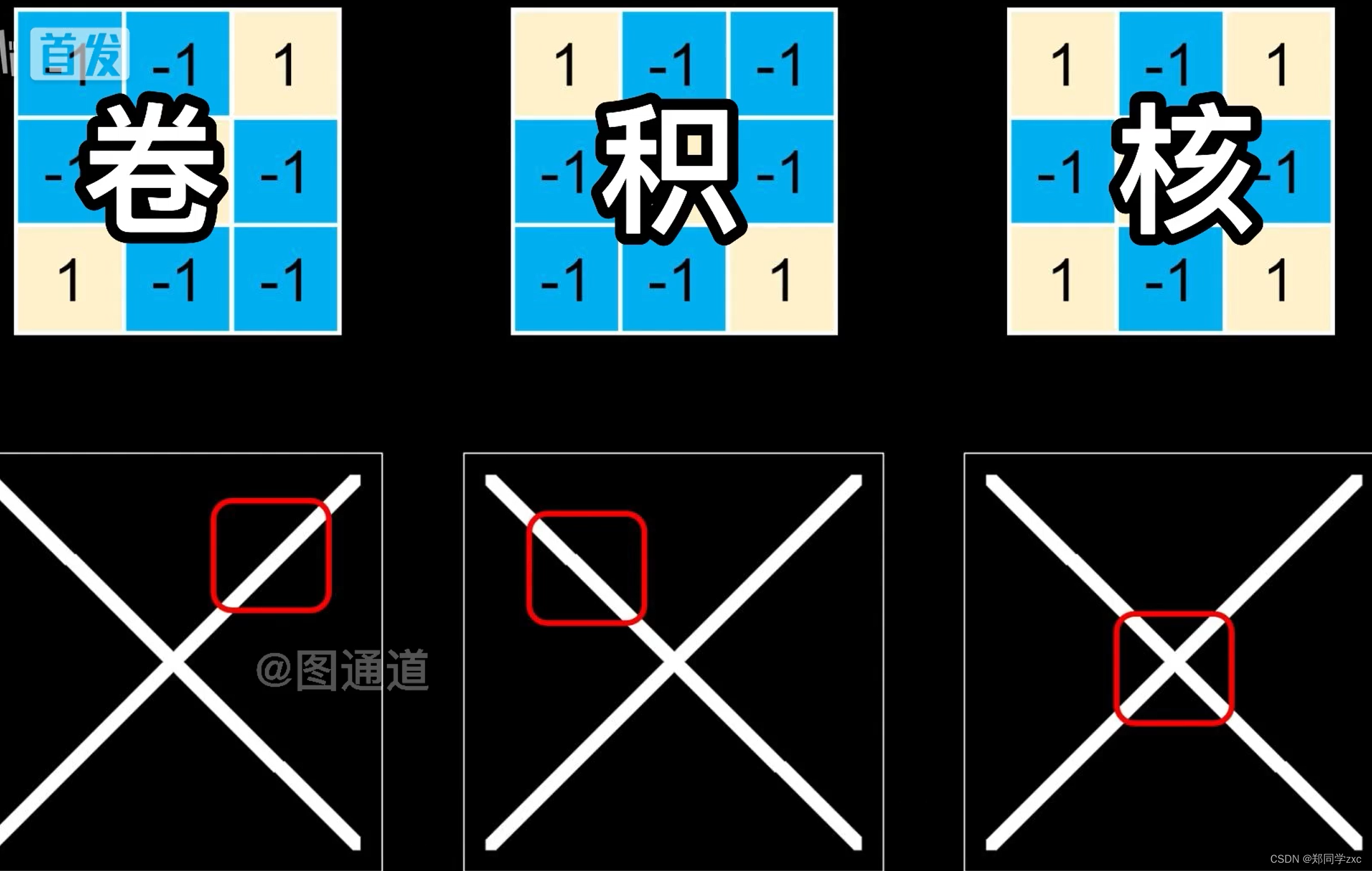
用卷积核扫描原始图像，将对应位置的元素相乘后相加，用一个新的矩阵记录新的矩阵。当被扫过的位置与卷积核的特征越接近计算得到的数值越大，在结果图片中的颜色月亮，特征越明显。单个卷积核处理单个特征。这个操作就是卷积

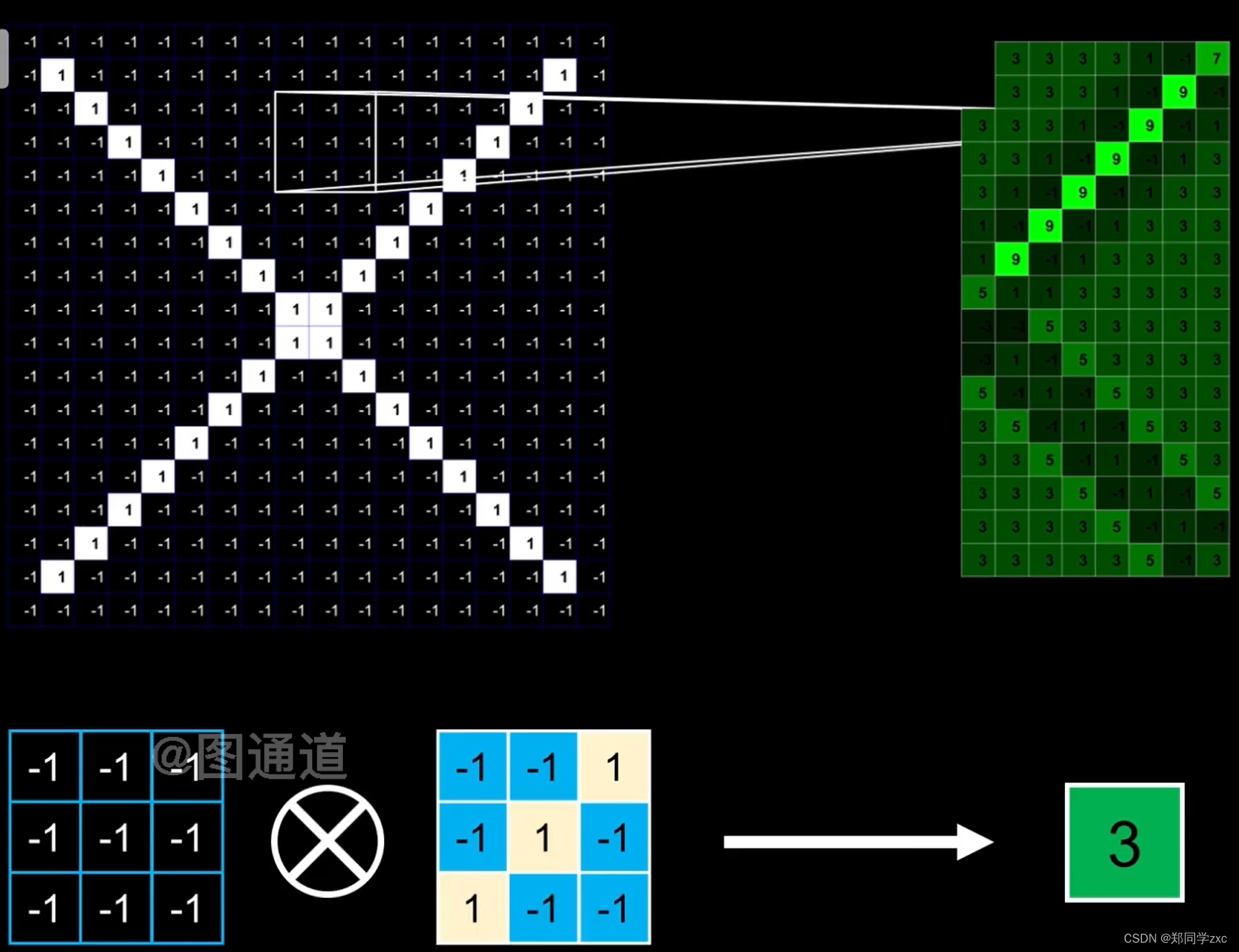
池化：
卷积后可能还会有很多弱的特征，并且此时图片数据还很大，还需要池化压缩数据，弱化所有特征。
原理：对一块区域内的结果去等效值，可以取最大值也可以取平均值

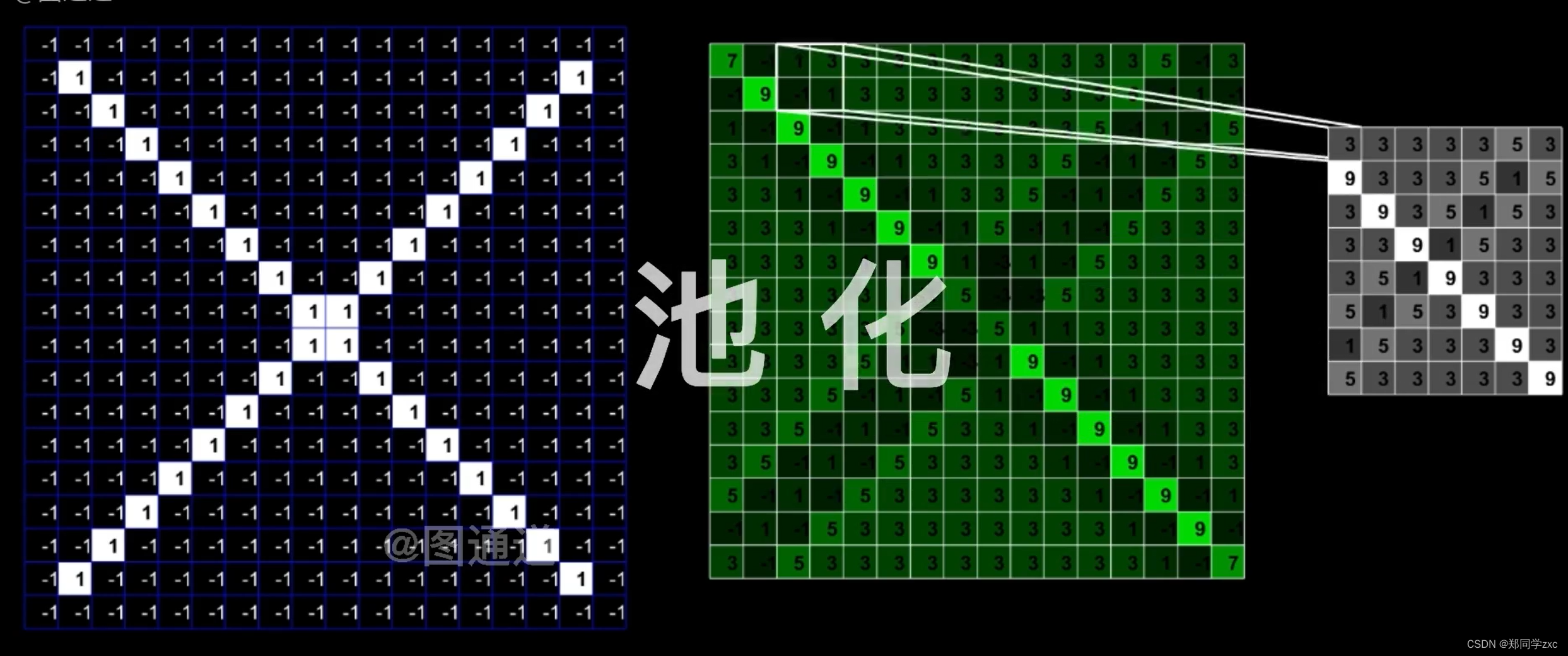
池化可以加快计算速度，也能避免过拟合


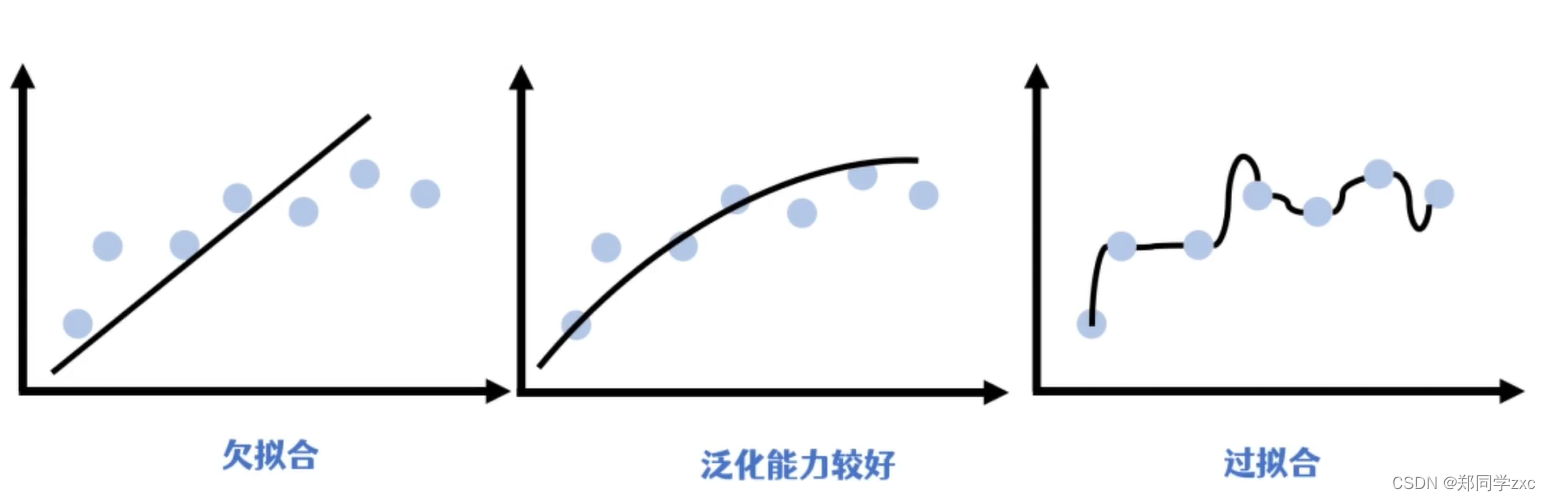
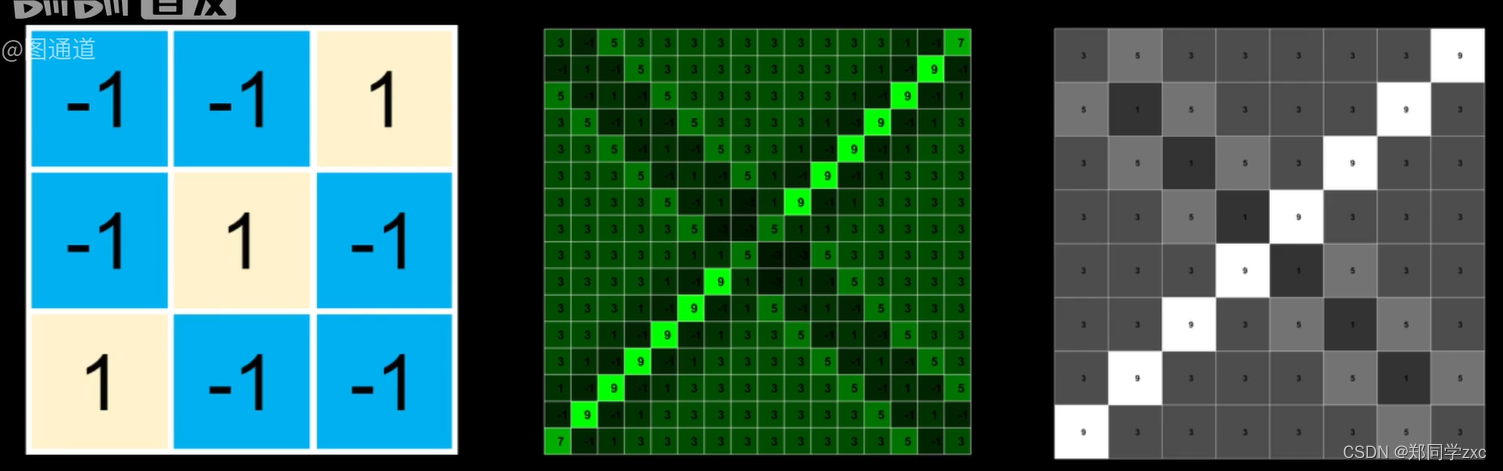
激活层：对卷积层输出进行一个非线性映射

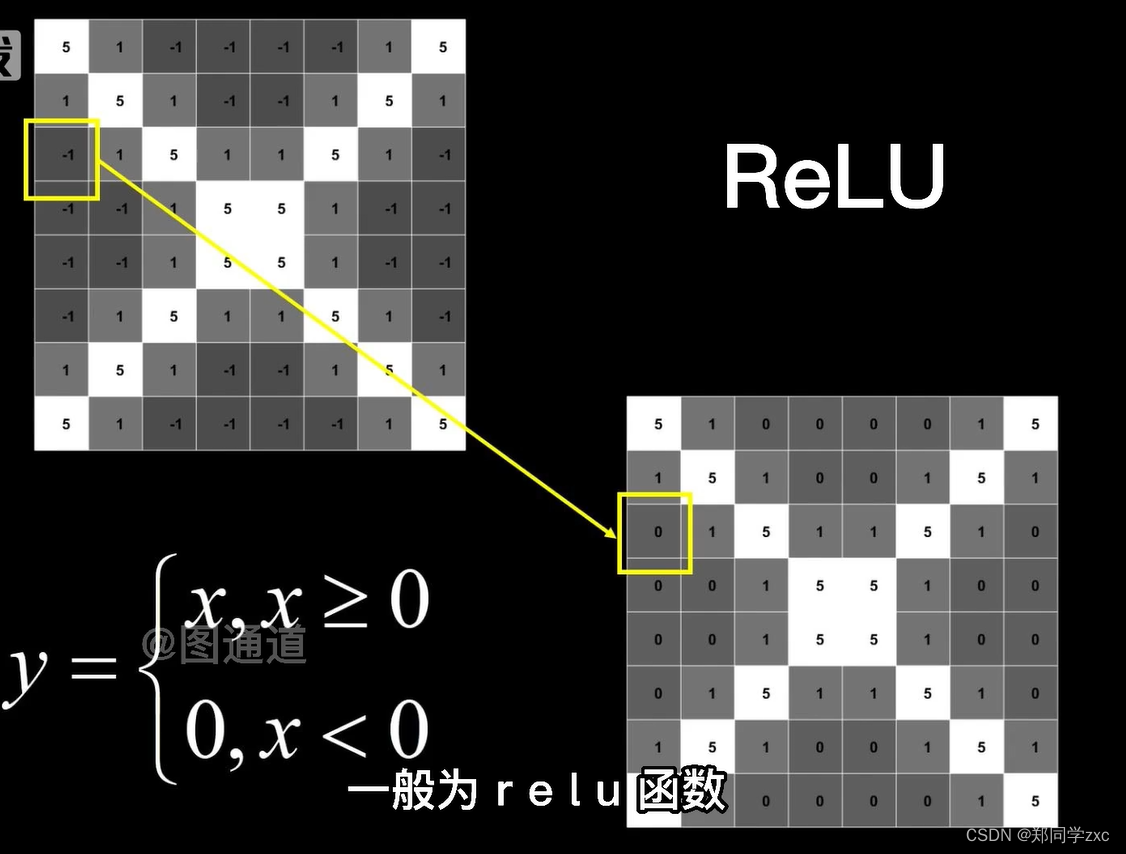
卷积是寻找特征池化是压缩数据激活是加强特征。三种操作可以重复的利用拼接组合，得到想要的图像

三、深度学习模型结构

深度神经网络是由多个单层非线性网络叠加而成的，常见的单层网络按照编码解码情况分为3类：只包含编码器部分、只包含解码器部分、既有编码器部分也有解码器部分。编码器提供从输入到隐含特征空间的自底向上的映射，解码器以重建结果尽可能接近原始输入为目标将隐含特征映射到输入空间。

人的视觉系统对信息的处理是分级的。从低级的提取边缘特征到形状（或者目标等），再到更高层的目标、目标的行为等，即底层特征组合成了高层特征，由低到高的特征表示越来越抽象。深度学习借鉴的这个过程就是建模的过程。

深度神经网络可以分为3类，

前馈深度网络(feed-forwarddeep networks, FFDN)，由多个编码器层叠加而成，如多层感知机(multi-layer perceptrons, MLP)、卷积神经网络(convolutionalneural networks, CNN)等。

反馈深度网络(feed-back deep networks, FBDN)，由多个解码器层叠加而成，如反卷积网络(deconvolutionalnetworks, DN)、层次稀疏编码网络(hierarchical sparse coding, HSC)等。

双向深度网络(bi-directionaldeep networks, BDDN)，通过叠加多个编码器层和解码器层构成(每层可能是单独的编码过程或解码过程，也可能既包含编码过程也包含解码过程)，如深度玻尔兹曼机(deep Boltzmann machines, DBM)、深度信念网络(deep beliefnetworks, DBN)、栈式自编码器(stacked auto-encoders, SAE)等。

1、 前溃深度网络

前馈神经网络是最初的人工神经网络模型之一。在这种网络中，信息只沿一个方向流动，从输入单元通过一个或多个隐层到达输出单元，在网络中没有封闭环路。典型的前馈神经网络有多层感知机和卷积神经网络等。F. Rosenblatt提出的感知机是最简单的单层前向人工神经网络，但随后M. Minsky等证明单层感知机无法解决线性不可分问题(如异或操作)，这一结论将人工神经网络研究领域引入到一个低潮期，直到研究人员认识到多层感知机可解决线性不可分问题，以及反向传播算法与神经网络结合的研究，使得神经网络的研究重新开始成为热点。但是由于传统的反向传播算法，具有收敛速度慢、需要大量带标签的训练数据、容易陷入局部最优等缺点，多层感知机的效果并不是十分理想。

1984年日本学者K. Fukushima等基于感受野概念，提出的神经认知机可看作卷积神经网络的一种特例。Y. Lecun等提出的卷积神经网络是神经认知机的推广形式。

卷积神经网络是由多个单层卷积神经网络组成的可训练的多层网络结构。每个单层卷积神经网络包括卷积、非线性变换和下采样3个阶段，其中下采样阶段不是每层都必需的。每层的输入和输出为一组向量构成的特征图(feature map)(第一层的原始输入信号可以看作一个具有高稀疏度的高维特征图)。

例如，输入部分是一张彩色图像，每个特征图对应的则是一个包含输入图像彩色通道的二维数组(对于音频输入，特征图对应的是一维向量；对于视频或立体影像，对应的是三维数组)；对应的输出部分，每个特征图对应的是表示从输入图片所有位置上提取的特定特征。

(1)、单层卷积神经网络：

卷积阶段，通过提取信号的不同特征实现输入信号进行特定模式的观测。其观测模式也称为卷积核，其定义源于由D. H. Hubel等基于对猫视觉皮层细胞研究提出的局部感受野概念。每个卷积核检测输入特征图上所有位置上的特定特征，实现同一个输入特征图上的权值共享。为了提取输入特征图上不同的特征，使用不同的卷积核进行卷积操作。卷积阶段的输入是由n1个n2n3大小的二维特征图构成的三维数组。每个特征图记为xi，该阶段的输出y，也是个三维数组，由m1个m2m3大小的特征图构成。在卷积阶段，连接输入特征图xi和输出特征图yj的权值记为wij，即可训练的卷积核(局部感受野)，卷积核的大小为k2*k3，输出特征图为yj。

非线性阶段，对卷积阶段得到的特征按照一定的原则进行筛选，筛选原则通常采用非线性变换的方式，以避免线性模型表达能力不够的问题。非线性阶段将卷积阶段提取的特征作为输入，进行非线性映射R=h(y)。传统卷积神经网络中非线性操作采用sigmoid、tanh 或softsign等饱和非线性(saturating nonlinearities)函数，近几年的卷积神经网络中多采用不饱和非线性(non-saturating nonlinearity)函数ReLU(rectifiedlinear units)。在训练梯度下降时，ReLU比传统的饱和非线性函数有更快的收敛速度，因此在训练整个网络时，训练速度也比传统的方法快很多。

下采样阶段，对每个特征图进行独立操作，通常采用平均池化(average pooling)或者最大池化(max pooling)的操作。

平均池化依据定义的邻域窗口计算特定范围内像素的均值PA，邻域窗口平移步长大于1(小于等于池化窗口的大小)；最大池化则将均值PA替换为最值PM输出到下个阶段。
池化操作后，输出特征图的分辨率降低，但能较好地保持高分辨率特征图描述的特征。
一些卷积神经网络完全去掉下采样阶段，通过在卷积阶段设置卷积核窗口滑动步长大于1达到降低分辨率的目的。

(2)、卷积神经网络：

将单层的卷积神经网络进行多次堆叠，前一层的输出作为后一层的输入，便构成卷积神经网络。其中每2个节点间的连线，代表输入节点经过卷积、非线性变换、下采样3个阶段变为输出节点，一般最后一层的输出特征图后接一个全连接层和分类器。

为了减少数据的过拟合，最近的一些卷积神经网络，在全连接层引入"Dropout"或"DropConnect"的方法，即在训练过程中以一定概率P将隐含层节点的输出值(对于"DropConnect"为输入权值)清0，而用反向传播算法更新权值时，不再更新与该节点相连的权值。但是这2种方法都会降低训练速度。

在训练卷积神经网络时，最常用的方法是采用反向传播法则以及有监督的训练方式。

网络中信号是前向传播的，即从输入特征向输出特征的方向传播，第1层的输入X，经过多个卷积神经网络层，变成最后一层输出的特征图O。将输出特征图O与期望的标签T进行比较，生成误差项E。通过遍历网络的反向路径，将误差逐层传递到每个节点，根据权值更新公式，更新相应的卷积核权值wij。
在训练过程中，网络中权值的初值通常随机初始化(也可通过无监督的方式进行预训练)，网络误差随迭代次数的增加而减少，并且这一过程收敛于一个稳定的权值集合，额外的训练次数呈现出较小的影响。

(3)、卷积神经网络的特点：

卷积神经网络的特点在于，采用原始信号(一般为图像)直接作为网络的输入，避免了传统识别算法中复杂的特征提取和图像重建过程。

局部感受野方法获取的观测特征与平移、缩放和旋转无关。

卷积阶段利用权值共享结构减少了权值的数量进而降低了网络模型的复杂度，这一点在输入特征图是高分辨率图像时表现得更为明显。同时，下采样阶段利用图像局部相关性的原理对特征图进行子抽样，在保留有用结构信息的同时有效地减少数据处理量。

CNN(convolutional neuralnetworks)是一种有监督深度的模型架构，尤其适合二维数据结构。目前研究与应用都较广泛，在行人检测、人脸识别、信号处理等领域均有新的成果与进展。它是带有卷积结构的深度神经网络，也是首个真正意义上成功训练多层网络的识别算法。

CNN与传统ANN 算法的主要区别在于权值共享以及非全连接。权值共享能够避免算法过拟合，通过拓扑结构建立层与层间非全连接空间关系来降低训练参数的数目，同时也是CNN的基本思想。CNN的实质是学习多个能够提取输入数据特征的滤波器，通过这些滤波器与输入数据进行逐层卷积及池化，逐级提取隐藏在数据中拓扑结构特征。随网络结构层层深入，提取的特征也逐渐变得抽象，最终获得输入数据的平移、旋转及缩放不变性的特征表示。较传统神经网络来说，CNN将特征提取与分类过程同时进行，避免了两者在算法匹配上的难点。

ANN: 代表“人工神经网络”（Artificial Neural Network）。人工神经网络是一种计算机模型，模仿了生物神经元之间的相互作用，通过学习和适应来执行任务，如分类、识别和预测。它由多个层次组成，每个层次都由许多节点或神经元组成，这些节点通过连接传递信息。ANN被广泛应用于机器学习和人工智能领域。

CNN主要由卷积层与下采样层交替重复出现构建网络结构，卷积层用来提取输入神经元数据的局部特征，下采样层用来对其上一层提取的数据进行缩放映射以减少训练数据量，也使提取的特征具有缩放不变性。一般来说，可以选择不同尺度的卷积核来提取多尺度特征，使提取的特征具有旋转、平移不变性。输入图像与可学习的核进行卷积，卷积后的数据经过激活函数得到一个特征图。卷积层的特征图可以由多个输入图组合获得，但对于同一幅输入图其卷积核参数是一致的，这也是权值共享的意义所在。卷积核的初始值并非随机设置，而是通过训练或者按照一定标准预先给定，如仿照生物视觉特征用Gabor 滤波器进行预处理。下采样层通过降低网络空间分辨率来增强缩放不变性。

下采样层（Downsampling Layer） :在卷积神经网络（Convolutional Neural Network，CNN）中，下采样层通常用于减少输入图像的尺寸，从而降低模型的计算复杂度和内存消耗。常见的下采样方法包括最大池化（Max Pooling）和平均池化（Average Pooling），它们分别在输入图像的不同区域取最大值或平均值，从而得到更小尺寸的输出特征图。下采样层通常与卷积层交替使用，以提取更高层次的特征。

CNN的输出层一般采用线性全连接，目前最常用的就是Softmax 分类方法。CNN的参数训练过程与传统的人工神经网络类似，采用反向传播算法，包括前向传播与反向传播2个重要阶段。

CNN实际应用中会遇到诸多问题，如网络权值的预学习问题，收敛条件以及非全连接规则等，这些均需要实际应用中进一步解决与优化。

卷积神经网络模型：

在无监督预训练出现之前，训练深度神经网络通常非常困难，而其中一个特例是卷积神经网络。卷积神经网络受视觉系统的结构启发而产生。

第一个卷积神经网络计算模型是在Fukushima的神经认知机中提出的，基于神经元之间的局部连接和分层组织图像转换，将有相同参数的神经元应用于前一层神经网络的不同位置，得到一种平移不变神经网络结构形式。后来，LeCun等人在该思想的基础上，用误差梯度设计并训练卷积神经网络，在一些模式识别任务上得到优越的性能。至今，基于卷积神经网络的模式识别系统是最好的实现系统之一，尤其在手写体字符识别任务上表现出非凡的性能。

LeCun的卷积神经网络由卷积层和子抽样层两种类型的神经网络层组成。每一层有一个拓扑图结构，即在接收域内，每个神经元与输入图像中某个位置对应的固定二维位置编码信息关联。在每层的各个位置分布着许多不同的神经元，每个神经元有一组输入权值，这些权值与前一层神经网络矩形块中的神经元关联；同一组权值和不同输入矩形块与不同位置的神经元关联。卷积神经网络是多层的感知器神经网络，每层由多个二维平面块组成，每个平面块由多个独立神经元组成。

为了使网络对平移、旋转、比例缩放以及其他形式的变换具有不变性，对网络的结构进行一些约束限制：

(1)、特征提取：每一个神经元从上一层的局部接收域得到输入，迫使其提取局部特征。

(2)、特征映射：网络的每一个计算层由多个特征映射组成，每个特征映射都以二维平面的形式存在，平面中的神经元在约束下共享相同的权值集。

(3)、子抽样：该计算层跟随在卷积层后，实现局部平均和子抽样，使特征映射的输出对平移等变换的敏感度下降。卷积神经网络通过使用接收域的局部连接，限制了网络结构。卷积神经网络的另一个特点是权值共享，但是由于同一隐层的神经元共享同一权值集，大大减少了自由参数的数量。

卷积神经网络本质上实现一种输入到输出的映射关系，能够学习大量输入与输出之间的映射关系，不需要任何输入和输出之间的精确数学表达式，只要用已知的模式对卷积神经网络加以训练，就可以使网络具有输入输出之间的映射能力。卷积神经网络执行的是有监督训练，在开始训练前，用一些不同的小随机数对网络的所有权值进行初始化。

卷积神经网络的训练分为两个阶段：

(1)、向前传播阶段：从样本集中抽取一个样本(X,Yp)，将x输入给网络，信息从输入层经过逐级变换传送到输出层，计算相应的实际输出Op；

(2)、向后传播阶段：也称为误差传播阶段。计算实际输出Op与理想输出Yp的差异。并按最小化误差的方法调整权值矩阵。

卷积神经网络的特征检测层通过训练数据来进行学习，避免了显式的特征提取，而是隐式地从训练数据中学习特征，而且同一特征映射面上的神经元权值相同，网络可以并行学习，这也是卷积神经网络相对于其他神经网络的一个优势。权值共享降低了网络的复杂性，特别是多维向量的图像可以直接输入网络这一特点避免了特征提取和分类过程中数据重建的复杂度。

卷积神经网络的成功依赖于两个假设：

(1)、每个神经元有非常少的输入，这有助于将梯度在尽可能多的层中进行传播；

(2)、分层局部连接结构是非常强的先验结构，特别适合计算机视觉任务，如果整个网络的参数处于合适的区域，基于梯度的优化算法能得到很好的学习效果。卷积神经网络的网络结构更接近实际的生物神经网络，在语音识别和图像处理方面具有独特的优越性，尤其是在视觉图像处理领域进行的实验，得到了很好的结果。

2、 反馈深度网络

与前馈网络不同，反馈网络并不是对输入信号进行编码，而是通过解反卷积或学习数据集的基，对输入信号进行反解。

前馈网络是对输入信号进行编码的过程，而反馈网络则是对输入信号解码的过程。典型的反馈深度网络有反卷积网络、层次稀疏编码网络等。

以反卷积网络为例，M. D. Zeiler等提出的反卷积网络模型和Y. LeCun等提出的卷积神经网络思想类似，但在实际的结构构件和实现方法上有所不同。

卷积神经网络是一种自底向上的方法，该方法的每层输入信号经过卷积、非线性变换和下采样3个阶段处理，进而得到多层信息。相比之下，反卷积网络模型的每层信息是自顶向下的，组合通过滤波器组学习得到的卷积特征来重构输入信号。

层次稀疏编码网络和反卷积网络非常相似，只是在反卷积网络中对图像的分解采用矩阵卷积的形式，而在稀疏编码中采用矩阵乘积的方式。

(1)、单层反卷积网络：反卷积网络是通过先验学习，对信号进行稀疏分解和重构的正则化方法。

(2)、反卷积网络：单层反卷积网络进行多层叠加，可得到反卷积网络。多层模型中，在学习滤波器组的同时进行特征图的推导，第L层的特征图和滤波器是由第L-1层的特征图通过反卷积计算分解获得。反卷积网络训练时，使用一组不同的信号y，求解C(y)，进行滤波器组f和特征图z的迭代交替优化。训练从第1层开始，采用贪心算法，逐层向上进行优化，各层间的优化是独立的。

(3)、反卷积网络的特点：反卷积网络的特点在于，通过求解最优化输入信号分解问题计算特征，而不是利用编码器进行近似，这样能使隐层的特征更加精准，更有利于信号的分类或重建。

自动编码器：

对于一个给定的神经网络，假设其输出等于输入（理想状态下），然后通过训练调整其参数得到每一层的权重，这样就可以得到输入的几种不同的表示，这些表示就是特征。

当在原有特征的基础上加入这些通过自动学习得到的特征时，可以大大提高精确度，这就是自动编码（AutoEncoder）。如果再继续加上一些约束条件的话，就可以得到新的深度学习方法。比如在自动编码的基础上加上稀疏性限制，就可得到稀疏自动编码器（Sparse AutoEncoder）。

稀疏自动编码器：

与CNN不同，深度自动编码器是一种无监督的神经网络学习架构。此类架构的基本结构单元为自动编码器，它通过对输入特征X按照一定规则及训练算法进行编码，将其原始特征利用低维向量重新表示。

自动编码器通过构建类似传统神经网络的层次结构，并假设输出Y与输入X相等，反复训练调整参数得到网络参数值。上述自编码器若仅要求X≈Y，且对隐藏神经元进行稀疏约束，从而使大部分节点值为0或接近0的无效值，便得到稀疏自动编码算法。一般情况下，隐含层的神经元数应少于输入X的个数，因为此时才能保证这个网络结构的价值。正如主成分分析（principal component analysis，PCA）算法，通过降低空间维数去除冗余，利用更少的特征来尽可能完整的描述数据信息。实际应用中将学习得到的多种隐层特征（隐层数通常多个）与原始特征共同使用，可以明显提高算法的识别精度。

自动编码器参数训练方法有很多，几乎可以采用任何连续化训练方法来训练参数。但由于其模型结构不偏向生成型，无法通过联合概率等定量形式确定模型合理性。稀疏性约束在深度学习算法优化中的地位越来越重要，主要与深度学习特点有关。大量的训练参数使训练过程复杂，且训练输出的维数远比输入的维数高，会产生许多冗余数据信息。加入稀疏性限制，会使学习到的特征更加有价值，同时这也符合人脑神经元响应稀疏性特点。

3、 双向深度网络

双向网络由多个编码器层和解码器层叠加形成，每层可能是单独的编码过程或解码过程，也可能同时包含编码过程和解码过程。双向网络的结构结合了编码器和解码器2类单层网络结构，双向网络的学习则结合了前馈网络和反馈网络的训练方法，通常包括单层网络的预训练和逐层反向迭代误差2个部分，单层网络的预训练多采用贪心算法：每层使用输入信号IL与权值w计算生成信号IL+1传递到下一层，信号IL+1再与相同的权值w计算生成重构信号I’L 映射回输入层，通过不断缩小IL与I’L间的误差，训练每层网络。网络结构中各层网络结构都经过预训练之后，再通过反向迭代误差对整个网络结构进行权值微调。其中单层网络的预训练是对输入信号编码和解码的重建过程，这与反馈网络训练方法类似；而基于反向迭代误差的权值微调与前馈网络训练方法类似。典型的双向深度网络有深度玻尔兹曼机、深度信念网络、栈式自编码器等。以深度玻尔兹曼机为例，深度玻尔兹曼机由R. Salakhutdinov等提出，它由多层受限玻尔兹曼机(restricted Boltzmann machine, RBM )叠加构成。

(1)、受限玻尔兹曼机：

玻尔兹曼机(Boltzmann machine, BM)是一种随机的递归神经网络，由G. E.Hinton等提出，是能通过学习数据固有内在表示、解决复杂学习问题的最早的人工神经网络之一。玻尔兹曼机由二值神经元构成，每个神经元只取0或1两种状态，状态1代表该神经元处于激活状态，0表示该神经元处于抑制状态。然而，即使使用模拟退火算法，这个网络的学习过程也十分慢。Hinton等提出的受限玻尔兹曼机去掉了玻尔兹曼机同层之间的连接，从而大大提高了学习效率。受限玻尔兹曼机分为可见层v以及隐层h，可见层和隐层的节点通过权值w相连接，2层节点之间是全连接，同层节点间互不相连。

受限玻尔兹曼机一种典型的训练方法：首先随机初始化可见层，然后在可见层与隐层之间交替进行吉布斯采样：用条件分布概率P(h|v)计算隐层；再根据隐层节点，同样用条件分布概率P(v|h)来计算可见层；重复这一采样过程直到可见层和隐层达到平稳分布。而Hinton提出了一种快速算法，称作对比离差(contrastive divergence, CD)学习算法。这种算法使用训练数据初始化可见层，只需迭代k次上述采样过程(即每次迭代包括从可见层更新隐层，以及从隐层更新可见层)，就可获得对模型的估计。

(2)、深度玻尔兹曼机：

将多个受限玻尔兹曼机堆叠，前一层的输出作为后一层的输入，便构成了深度玻尔兹曼机。网络中所有节点间的连线都是双向的。深度玻尔兹曼机训练分为2个阶段：预训练阶段和微调阶段。在预训练阶段，采用无监督的逐层贪心训练方法来训练网络每层的参数，即先训练网络的第1个隐含层，然后接着训练第2，3，…个隐含层，最后用这些训练好的网络参数值作为整体网络参数的初始值。预训练之后，将训练好的每层受限玻尔兹曼机叠加形成深度玻尔兹曼机，利用有监督的学习对网络进行训练(一般采用反向传播算法)。由于深度玻尔兹曼机随机初始化权值以及微调阶段采用有监督的学习方法，这些都容易使网络陷入局部最小值。而采用无监督预训练的方法，有利于避免陷入局部最小值问题。

受限玻尔兹曼机（RBM，RestrictBoltzmann Machine）：

假设有一个二部图（二分图），一层是可视层v（即输入层），一层是隐层h，每层内的节点之间设有连接。在已知v时，全部的隐藏节点之间都是条件独立的（因为这个模型是二部图），即p(h|v) = p(h1|v1) … p(hn|v)。同样的，在已知隐层h的情况下，可视节点又都是条件独立的，又因为全部的h和v满足玻尔兹曼分布，所以当输入v的时候，通过p(h|v)可得到隐层h，得到h之后，通过p(v|h)又可以重构可视层v。通过调整参数，使得从隐层计算得到的可视层与原来的可视层有相同的分布。这样的话，得到的隐层就是可视层的另外一种表达，即可视层的特征表示。若增加隐层的层数，可得到深度玻尔兹曼机（DBM，Deep Boltzmann Machine）。若在靠近可视层v的部分使用贝叶斯信念网，远离可视层的部分使用RBM，那么就可以得到一个深度信念网络（DBNs，Deep Belief Nets）。

受限玻尔兹曼机模型是玻尔兹曼机（BM，BoltzmannMachine）模型的一种特殊形式，其特殊性就在于同层内的节点没有连接，是以二部图的形式存在。

由于受限玻尔兹曼机是一种随机网络，而随机神经网络又是根植于统计力学的，所以受统计力学能量泛函的启发引入了能量函数。在随机神经网络中，能量函数是用来描述整个系统状态的测度。网络越有序或概率分布越集中，网络的能量就越小；反之，网络越无序或概率分布不集中，那么网络的能量就越大。所以当网络最稳定时，能量函数的值最小。

深度信念神经网络：

深度结构的训练大致有无监督的训练和有监督的训练两种，而且两者拥有不一样的模型架构。比如卷积神经网络就是一种有监督下的深度结构学习模型（即需要大量有标签的训练样本），但深度信念网络是一种无监督和有监督混合下的深度结构学习模型（即需要一部分无标签的训练样本和一部分有标签的样本）。

一个典型的深度信念网络可看成多个受限玻尔兹曼机的累加，而DBNs则是一个复杂度较高的有向无环图。

深度信念网络在训练的过程中，所需要学习的即是联合概率分布。在机器学习领域中，其所表示的就是对象的生成模型。如果想要全局优化具有多隐层的深度信念网络是比较困难的。这个时候，可以运用贪婪算法，即逐层进行优化，每次只训练相邻两层的模型参数，通过逐层学习来获得全局的网络参数。这种训练方法（非监督逐层贪婪训练）已经被Hinton证明是有效的，并称其为相对收敛（contrastive divergence）。

深度信任网络模型：DBN可以解释为贝叶斯概率生成模型，由多层随机隐变量组成，上面的两层具有无向对称连接，下面的层得到来自上一层的自顶向下的有向连接，最底层单元的状态为可见输入数据向量。DBN由若干结构单元堆栈组成，结构单元通常为RBM。堆栈中每个RBM单元的可视层神经元数量等于前一RBM单元的隐层神经元数量。根据深度学习机制，采用输入样例训练第一层RBM单元，并利用其输出训练第二层RBM模型，将RBM模型进行堆栈通过增加层来改善模型性能。在无监督预训练过程中，DBN编码输入到顶层RBM后解码顶层的状态到最底层的单元实现输入的重构。作为DBN的结构单元，RBM与每一层DBN共享参数。

RBM是一种特殊形式的玻尔兹曼机(Boltzmannmachine，BM)，变量之间的图模型连接形式有限制，只有可见层节点与隐层节点之间有连接权值，而可见层节点与可见层节点及隐层节点与隐层节点之间无连接。BM是基于能量的无向图概率模型。

BM的典型训练算法有变分近似法、随机近似法(stochastic approximation procedure，SAP)、对比散度算法(contrastivedivergence，CD)、持续对比散度算法(persistent contrastive divergence，PCD)、快速持续对比散度算法(fastpersistent contrastive divergence，FPCD)和回火MCMC算法等。

堆栈自编码网络模型：堆栈自编码网络的结构与DBN类似，由若干结构单元堆栈组成，不同之处在于其结构单元为自编码模型(auto—en—coder)而不是RBM。自编码模型是一个两层的神经网络，第一层称为编码层，第二层称为解码层。

堆栈自编码网络的结构单元除了自编码模型之外，还可以使用自编码模型的一些变形，如降噪自编码模型和收缩自编码模型等。降噪自编码模型避免了一般的自编码模型可能会学习得到无编码功能的恒等函数和需要样本的个数大于样本的维数的限制，尝试通过最小化降噪重构误差，从含随机噪声的数据中重构真实的原始输入。降噪自编码模型使用由少量样本组成的微批次样本执行随机梯度下降算法，这样可以充分利用图处理单元(graphical processing unit，GPU)的矩阵到矩阵快速运算使得算法能够更快地收敛。

收缩自编码模型的训练目标函数是重构误差和收缩罚项(contraction penalty)的总和，通过最小化该目标函数使已学习到的表示C(x)尽量对输入x保持不变。为了避免出现平凡解，编码器权值趋于零而解码器权值趋于无穷，并且收缩自编码模型采用固定的权值，令解码器权值为编码器权值的置换阵。与其他自编码模型相比，收缩自编码模型趋于找到尽量少的几个特征值，特征值的数量对应局部秩和局部维数。收缩自编码模型可以利用隐单元建立复杂非线性流形模型。

MKMs： 受SVM算法中核函数的启发，在深度模型结构中加入核函数，构建一种基于核函数的深度学习模型。MKMs深度模型，如同深度信念网络（deep belief network，DBNs），反复迭代核PCA 来逼近高阶非线性函数，每一层核PCA 的输出作为下一层核PCA 的输入。作者模拟大型神经网络计算方法创建核函数族，并将其应用在训练多层深度学习模型中。L层MKMs深度模型的训练过程如下：

(1)、去除输入特征中无信息含量的特征；

(2)、重复L次：A、计算有非线性核产生特征的主成分；B、去除无信息含量的主成分特征；

(3)、采用Mahalanobis距离进行最近邻分类。

在参数训练阶段，采用核主成分分析法（kernelprincipal component analysis，KPCA）进行逐层贪婪无监督学习，并提取第k层数据特征中的前nk 主成分，此时第k+1层便获得第k层的低维空间特征。为进一步降低每层特征的维数，采用有监督的训练机制进行二次筛选：首先，根据离散化特征点边缘直方图，估计它与类标签之间的互信息，将nk 主成分进行排序；其次，对于不同的k 和w 采用KNN 聚类方法，每次选取排序最靠前的w验证集上的特征并计算其错误率，最终选择错误率最低的w个特征。该模型由于特征选取阶段无法并行计算，导致交叉验证阶段需耗费大量时间。据此，提出了一种改进方法，通过在隐藏层采用有监督的核偏最小二乘法（kernel partial least squares，KPLS）来优化此问题。

DeSTIN： 目前较成熟的深度学习模型大多建立在空间层次结构上，很少对时效性（temporal）有所体现。相关研究表明，人类大脑的运行模式是将感受到的模式与记忆存储的模式进行匹配，并对下一时刻的模式进行预测，反复进行上述步骤，这个过程包含了时空信息。因此在深度结构中将时效性考虑在内，会更接近人脑的工作模式。DeSTIN便是基于这种理念被提出的。DeSTIN 是一种基于贝叶斯推理理论、动态进行模式分类的深度学习架构，它是一种区分性的层次网络结构。在该深度模型中，数据间的时空相关性通过无监督方式来学习。网络的每一层的每个节点结构一致，且包含多个聚类中心，通过聚类和动态建模来模拟输入。每个节点通过贝叶斯信念推理输出该节点信念值，根据信念值提取整个DeSTIN网络的模式特征，最后一层网络输出特征可以输入分类器如SVM中进行模式分类。

DeSTIN 模型的每一个节点都用来学习一个模式时序，底层节点通过对输入数据的时间与空间特征进行提取，改变其信念值，输入到下一层。由于每一个节点结构相同，训练时可采样并行计算，节约运算资源。该模型最重要的步骤就是信念值更新算法。信念值更新算法同时考虑了数据的时间与空间特征。目前将时效性考虑在内的深度学习架构虽然不是很成熟，但也逐渐应用在不同领域，也是深度学习模型未来发展的一个新方向。

四、 深度学习训练算法

实验结果表明，对深度结构神经网络采用随机初始化的方法，基于梯度的优化使训练结果陷入局部极值，而找不到全局最优值，并且随着网络结构层次的加深，更难以得到好的泛化性能，使得深度结构神经网络在随机初始化后得到的学习结果甚至不如只有一个或两个隐层的浅结构神经网络得到的学习结果好。

由于随机初始化深度结构神经网络的参数得到的训练结果和泛化性能都很不理想，在2006年以前，深度结构神经网络在机器学习领域文献中并没有进行过多讨论。

通过实验研究发现，用无监督学习算法对深度结构神经网络进行逐层预训练，能够得到较好的学习结果。最初的实验对每层采用RBM生成模型，后来的实验采用自编码模型来训练每一层，两种模型得到相似的实验结果。

一些实验和研究结果证明了无监督预训练相比随机初始化具有很大的优势，无监督预训练不仅初始化网络得到好的初始参数值，而且可以提取关于输入分布的有用信息，有助于网络找到更好的全局最优解。对深度学习来说，无监督学习和半监督学习是成功的学习算法的关键组成部分，

主要原因包括以下几个方面：

(1)、与半监督学习类似，深度学习中缺少有类标签的样本，并且样例大多无类标签；

(2)、逐层的无监督学习利用结构层上的可用信息进行学习，避免了监督学习梯度传播的问题，可减少对监督准则函数梯度给出的不可靠更新方向的依赖；

(3)、无监督学习使得监督学习的参数进入一个合适的预置区域内，在此区域内进行梯度下降能够得到很好的解；

(4)、在利用深度结构神经网络构造一个监督分类器时，无监督学习可看做学习先验信息，使得深度结构神经网络训练结果的参数在大多情况下都具有意义；

(5)、在深度结构神经网络的每一层采用无监督学习将一个问题分解成若干与多重表示水平提取有关的子问题，是一种常用的可行方法，可提取输入分布较高水平表示的重要特征信息。

基于上述思想，Hinton等人在2006年引入了DBN并给出了一种训练该网络的贪婪逐层预训练算法。

贪婪逐层无监督预训练学习的基本思想为：

首先采用无监督学习算法对深度结构神经网络的较低层进行训练，生成第一层深度结构神经网络的初始参数值；

然后将第一层的输出作为另外一层的输入，同样采用无监督学习算法对该层参数进行初始化。

在对多层进行初始化后，用监督学习算法对整个深度结构神经网络进行微调，得到的学习性能具有很大程度的提高。

以堆栈自编码网络为例，深度结构神经网络的训练过程如下：

(1)、将第一层作为一个自编码模型，采用无监督训练，使原始输入的重建误差最小；

(2)、将自编码模型的隐单元输出作为另一层的输入；

(3)、按步骤(2)迭代初始化每一层的参数；

(4)、采用最后一个隐层的输出作为输入施加于一个有监督的层(通常为输出层)，并初始化该层的参数；

(5)、根据监督准则调整深度结构神经网络的所有参数，堆栈所有自编码模型组成堆栈自编码网络。

基本的无监督学习方法在2006年被Hinton等人提出用于训练深度结构神经网络，该方法的学习步骤如下：

(1)、令h0(x)=x为可观察的原始输入x的最低阶表示;

(2)、对l=1,…,L,训练无监督学习模型，将可观察数据看做l-1阶上表示的训练样例hl-1(x)，训练后产生下一阶的表示hl(x)=Rl(hl-1(x)).

随后出现了一些该算法的变形拓展，最常见的是有监督的微调方法,该方法的学习步骤如下所示：

(1)、初始化监督预测器：a、用参数表示函数hL(x);b、将hL(x)作为输入得到线性或非线性预测器；

(2)、基于已标记训练样本对(x,y)采用监督训练准则微调监督预测器，在表示阶段和预测器阶段优化参数。

深度学习的训练过程：

1、自下向上的非监督学习：采用无标签数据分层训练各层参数，这是一个无监督训练的过程（也是一个特征学习的过程），是和传统神经网络区别最大的部分。具体是：用无标签数据去训练第一层，这样就可以学习到第一层的参数，在学习得到第n-1层后，再将第n-1层的输出作为第n层的输入，训练第n层，进而分别得到各层的参数。这称为网络的预训练。

2、自顶向下的监督学习：在预训练后，采用有标签的数据来对网络进行区分性训练，此时误差自顶向下传输。预训练类似传统神经网络的随机初始化，但由于深度学习的第一步不是随机初始化而是通过学习无标签数据得到的，因此这个初值比较接近全局最优，所以深度学习效果好很多程序上归功于第一步的特征学习过程。

使用到的学习算法包括：
(1)、深度费希尔映射方法：

Wong等人提出一种新的特征提取方法----正则化深度费希尔映射(regularized deep Fisher mapping，RDFM)方法，学习从样本空间到特征空间的显式映射，根据Fisher准则用深度结构神经网络提高特征的区分度。深度结构神经网络具有深度非局部学习结构，从更少的样本中学习变化很大的数据集中的特征，显示出比核方法更强的特征识别能力，同时RDFM方法的学习过程由于引入正则化因子，解决了学习能力过强带来的过拟合问题。在各种类型的数据集上进行实验，得到的结果说明了在深度学习微调阶段运用无监督正则化的必要性。

(2)、非线性变换方法：

Raiko等人提出了一种非线性变换方法，该变换方法使得多层感知器(multi—layer perceptron，MLP)网络的每个隐神经元的输出具有零输出和平均值上的零斜率，使学习MLP变得更容易。将学习整个输入输出映射函数的线性部分和非线性部分尽可能分开，用shortcut权值(shortcut weight)建立线性映射模型，令Fisher信息阵接近对角阵，使得标准梯度接近自然梯度。通过实验证明非线性变换方法的有效性，该变换使得基本随机梯度学习与当前的学习算法在速度上不相上下，并有助于找到泛化性能更好的分类器。用这种非线性变换方法实现的深度无监督自编码模型进行图像分类和学习图像的低维表示的实验，说明这些变换有助于学习深度至少达到五个隐层的深度结构神经网络，证明了变换的有效性，提高了基本随机梯度学习算法的速度，有助于找到泛化性更好的分类器。

(3)、稀疏编码对称机算法：

Ranzato等人提出一种新的有效的无监督学习算法----稀疏编码对称机(sparse encoding symmetric machine，SESM)，能够在无须归一化的情况下有效产生稀疏表示。SESM的损失函数是重构误差和稀疏罚函数的加权总和，基于该损失函数比较和选择不同的无监督学习机，提出一种相关的迭代在线学习算法，并在理论和实验上将SESM与RBM和PCA进行比较，在手写体数字识别MNIST数据集和实际图像数据集上进行实验，表明该方法的优越性。

(4)、迁移学习算法：

在许多常见学习场景中训练和测试数据集中的类标签不同，必须保证训练和测试数据集中的相似性进行迁移学习。Mesnil等人研究了用于无监督迁移学习场景中学习表示的不同种类模型结构，将多个不同结构的层堆栈使用无监督学习算法用于五个学习任务，并研究了用于少量已标记训练样本的简单线性分类器堆栈深度结构学习算法。Bengio等人研究了无监督迁移学习问题，讨论了无监督预训练有用的原因，如何在迁移学习场景中利用无监督预训练，以及在什么情况下需要注意从不同数据分布得到的样例上的预测问题。

(5)、自然语言解析算法：

Collobert基于深度递归卷积图变换网络(graphtransformer network，GTN)提出一种快速可扩展的判别算法用于自然语言解析，将文法解析树分解到堆栈层中，只用极少的基本文本特征，得到的性能与现有的判别解析器和标准解析器的性能相似，而在速度上有了很大提升。

(6)、学习率自适应方法：

学习率自适应方法可用于提高深度结构神经网络训练的收敛性并且去除超参数中的学习率参数，其中包括全局学习率、层次学习率、神经元学习率和参数学习率等。最近研究人员提出了一些新的学习率自适应方法，如Duchi等人提出的自适应梯度方法和Schaul等人提出的学习率自适应方法；Hinton提出了收缩学习率方法使得平均权值更新在权值大小的1/1000数量级上；LeRoux等人提出自然梯度的对角低秩在线近似方法，并说明该算法在一些学习场景中能加速训练过程。

五、 深度学习的优点

深度学习与浅学习相比具有许多优点：

1、 在网络表达复杂目标函数的能力方面，浅结构神经网络有时无法很好地实现高变函数等复杂高维函数的表示，而用深度结构神经网络能够较好地表征。

2、 在网络结构的计算复杂度方面，当用深度为k的网络结构能够紧凑地表达某一函数时，在采用深度小于k的网络结构表达该函数时，可能需要增加指数级规模数量的计算因子，大大增加了计算的复杂度。另外，需要利用训练样本对计算因子中的参数值进行调整，当一个网络结构的训练样本数量有限而计算因子数量增加时，其泛化能力会变得很差。

3、 在仿生学角度方面，深度学习网络结构是对人类大脑皮层的最好模拟。与大脑皮层一样，深度学习对输入数据的处理是分层进行的，用每一层神经网络提取原始数据不同水平的特征。

4、 在信息共享方面，深度学习获得的多重水平的提取特征可以在类似的不同任务中重复使用，相当于对任务求解提供了一些无监督的数据，可以获得更多的有用信息。

5、 深度学习比浅学习具有更强的表示能力，而由于深度的增加使得非凸目标函数产生的局部最优解是造成学习困难的主要因素。反向传播基于局部梯度下降，从一些随机初始点开始运行，通常陷入局部极值，并随着网络深度的增加而恶化，不能很好地求解深度结构神经网络问题。2006年，Hinton等人提出的用于深度信任网络(deep belief network，DBN)的无监督学习算法，解决了深度学习模型优化困难的问题。求解DBN方法的核心是贪婪逐层预训练算法，在与网络大小和深度呈线性的时间复杂度上优化DBN的权值，将求解的问题分解成为若干更简单的子问题进行求解。

6、 深度学习方法试图找到数据的内部结构，发现变量之间的真正关系形式。大量研究表明，数据表示的方式对训练学习的成功产生很大的影响，好的表示能够消除输入数据中与学习任务无关因素的改变对学习性能的影响，同时保留对学习任务有用的信息。深度学习中数据的表示有局部表示(local representation)、分布表示(distributed representation)，和稀疏分布表示(sparsedistributed representation) 三种表示形式。学习输入层、隐层和输出层的单元均取值0或1。举个简单的例子，整数i∈{1，2，…，N}的局部表示为向量R(i)，该向量有N位，由1个1和N-1个0组成，即Rj(i)=1i=j。分布表示中的输入模式由一组特征表示，这些特征可能存在相互包含关系，并且在统计意义上相互独立。对于例子中相同整数的分布表示有log2N位的向量，这种表示更为紧凑，在解决降维和局部泛化限制方面起到帮助作用。稀疏分布表示介于完全局部表示和非稀疏分布表示之间，稀疏性的意思为表示向量中的许多单元取值为0。对于特定的任务需要选择合适的表示形式才能对学习性能起到改进的作用。当表示一个特定的输入分布时，一些结构是不可能的，因为它们不相容。例如在语言建椁中，运用局部表示可以直接用词汇表中的索引编码词的特性，而在句法特征、形态学特征和语义特征提取中，运用分布表示可以通过连接一个向量指示器来表示一个词。分布表示由于其具有的优点，常常用于深度学习中表示数据的结构。由于聚类簇之间在本质上互相不存在包含关系，因此聚类算法不专门建立分布表示，而独立成分分析(independent component analysis，ICA)和主成分分析(principalcomponent analysis，PCA)通常用来构造数据的分布表示。

六、 深度学习已有的应用

深度学习架构由多层非线性运算单元组成，每个较低层的输出作为更高层的输入，可以从大量输入数据中学习有效的特征表示，学习到的高阶表示中包含输入数据的许多结构信息，是一种从数据中提取表示的好方法，能够用于分类、回归和信息检索等特定问题中。

深度学习目前在很多领域都优于过去的方法。如语音和音频识别、图像分类及识别、人脸识别、视频分类、行为识别、图像超分辨率重建、纹理识别、行人检测、场景标记、门牌识别、手写体字符识别、图像检索、人体运行行为识别等。

1、 深度学习在语音识别、合成及机器翻译中的应用

微软研究人员使用深度信念网络对数以千计的senones(一种比音素小很多的建模单元)直接建模,提出了第1个成功应用于大词汇量语音识别系统的上下文相关的深层神经网络–隐马尔可夫混合模型(CD-DNN-HMM)，比之前最领先的基于常规CD-GMM-HMM的大词汇量语音识别系统相对误差率减少16%以上。随后又在含有300h语音训练数据的Switchboard标准数据集上对CD-DNN-HMM模型进行评测。基准测试字词错误率为18.5%，与之前最领先的常规系统相比，相对错误率减少了33%。

H. Zen等提出一种基于多层感知机的语音合成模型。该模型先将输入文本转换为一个输入特征序列，输入特征序列的每帧分别经过多层感知机映射到各自的输出特征，然后采用算法，生成语音参数，最后经过声纹合成生成语音。训练数据包含由一名女性专业演讲者以美国英语录制的3.3万段语音素材，其合成结果的主观评价和客观评价均优于基于HMM方法的模型。

K. Cho等提出一种基于循环神经网络(recurrentneural network, RNN)的向量化定长表示模型(RNNenc模型)，应用于机器翻译。该模型包含2个RNN，一个RNN用于将一组源语言符号序列编码为一组固定长度的向量，另一个RNN将该向量解码为一组目标语言的符号序列。在该模型的基础上，D. Bahdanau等克服了固定长度的缺点(固定长度是其效果提升的瓶颈)，提出了RNNsearch的模型。该模型在翻译每个单词时，根据该单词在源文本中最相关信息的位置以及已翻译出的其他单词，预测对应于该单词的目标单词。该模型包含一个双向RNN作为编码器，以及一个用于单词翻译的解码器。在进行目标单词位置预测时，使用一个多层感知机模型进行位置对齐。采用BLEU评价指标，RNNsearch模型在ACL2014机器翻译研讨会(ACL WMT 2014)提供的英/法双语并行语料库上的翻译结果评分均高于RNNenc模型的评分，略低于传统的基于短语的翻译系统Moses(本身包含具有4.18 亿个单词的多语言语料库)。另外，在剔除包含未知词汇语句的测试预料库上，RNNsearch的评分甚至超过了Moses。

2、 深度学习在图像分类及识别中的应用

(1)、深度学习在大规模图像数据集中的应用：

A. Krizhevsky等首次将卷积神经网络应用于ImageNet大规模视觉识别挑战赛(ImageNetlargescale visual recognition challenge, ILSVRC)中，所训练的深度卷积神经网络在ILSVRC—2012挑战赛中，取得了图像分类和目标定位任务的第一。其中，图像分类任务中，前5选项错误率为15.3%，远低于第2名的26.2%的错误率；在目标定位任务中，前5选项错误率34%，也远低于第2名的50%。

在ILSVRC—2013比赛中，M. D. Zeiler等采用卷积神经网络的方法，对A. Krizhevsky的方法进行了改进，并在每个卷积层上附加一个反卷积层用于中间层特征的可视化，取得了图像分类任务的第一名。其前5 选项错误率为11.7%，如果采用ILSVRC—2011 数据进行预训练，错误率则降低到11.2%。

在目标定位任务中，P. Sermanet等采用卷积神经网络结合多尺度滑动窗口的方法，可同时进行图像分类、定位和检测，是比赛中唯一一个同时参加所有任务的队伍。

多目标检测任务中，获胜队伍的方法在特征提取阶段没有使用深度学习模型，只在分类时采用卷积网络分类器进行重打分。

在ILSVRC—2014比赛中，几乎所有的参赛队伍都采用了卷积神经网络及其变形方法。其中GoogLeNet小组采用卷积神经网络结合Hebbian理论提出的多尺度的模型，以6.7%的分类错误，取得图形分类"指定数据"组的第一名；CASIAWS小组采用弱监督定位和卷积神经网络结合的方法，取得图形分类"额外数据"组的第一名，其分类错误率为11%。

在目标定位任务中，VGG小组在深度学习框架Caffe的基础上，采用3个结构不同的卷积神经网络进行平均评估，以26%的定位错误率取得"指定数据"组的第一名；Adobe 组选用额外的2000类ImageNet数据训练分类器，采用卷积神经网络架构进行分类和定位，以30%的错误率，取得了"额外数据"组的第一名。

在多目标检测任务中，NUS小组采用改进的卷积神经网络----网中网(networkin network, NIN)与多种其他方法融合的模型，以37%的平均准确率(mean average precision, mAP)取得"提供数据"组的第一名；GoogLeNet以44%的平均准确率取得"额外数据"组的第一名。

从深度学习首次应用于ILSVRC挑战赛并取得突出的成绩，到2014年挑战赛中几乎所有参赛队伍都采用深度学习方法，并将分类识错率降低到6.7%，可看出深度学习方法相比于传统的手工提取特征的方法在图像识别领域具有巨大优势。

(2)、深度学习在人脸识别中的应用：

基于卷积神经网络的学习方法，香港中文大学的DeepID项目以及Facebook的DeepFace项目在户外人脸识别(labeledfaces in the wild, LFW)数据库上的人脸识别正确率分别达97.45%和97.35%，只比人类识别97.5%的正确率略低一点点。DeepID项目采用4层卷积神经网络(不含输入层和输出层)结构，DeepFace采用5层卷积神经网络(不含输入层和输出层，其中后3层没有采用权值共享以获得不同的局部统计特征)结构，之后，采用基于卷积神经网络的学习方法。香港中文大学的DeepID2项目将识别率提高到了99.15%，超过目前所有领先的深度学习和非深度学习算法在LFW 数据库上的识别率以及人类在该数据库的识别率。DeepID2项目采用和DeepID项目类似的深度结构，包含4个卷积层，其中第3层采用2*2邻域的局部权值共享，第4层没有采用权值共享，且输出层与第3、4层都全连接。

(3)、深度学习在手写体字符识别中的应用：

Bengio等人运用统计学习理论和大量的实验工作证明了深度学习算法非常具有潜力，说明数据中间层表示可以被来自不同分布而相关的任务和样例共享，产生更好的学习效果，并且在有62个类别的大规模手写体字符识别场景上进行实验，用多任务场景和扰动样例来得到分布外样例，并得到非常好的实验结果。Lee等人对RBM进行拓展，学习到的模型使其具有稀疏性，可用于有效地学习数字字符和自然图像特征。Hinton等人关于深度学习的研究说明了如何训练深度s型神经网络来产生对手写体数字文本有用的表示，用到的主要思想是贪婪逐层预训练RBM之后再进行微调。

3、 深度学习在行人检测中的应用

将CNN应用到行人检测中，提出一种联合深度神经网络模型（unified deep net，UDN）。输入层有3个通道，均为对YUV空间进行相关变换得到，实验结果表明在此实验平台前提下，此输入方式较灰色像素输入方式正确率提高8%。第一层卷积采用64个不同卷积核，初始化采用Gabor滤波器，第二层卷积采用不同尺度的卷积核，提取人体的不同部位的具体特征，训练过程作者采用联合训练方法。最终实验结果在Caltech及ETH 数据集上错失率较传统的人体检测HOG-SVM算法均有明显下降，在Caltech库上较目前最好的算法错失率降低9%。

4、 深度学习在视频分类及行为识别中的应用

A. Karpathy等基于卷积神经网络提供了一种应用于大规模视频分类上的经验评估模型，将Sports-1M数据集的100万段YouTube视频数据分为487类。该模型使用4种时空信息融合方法用于卷积神经网络的训练，融合方法包括单帧(single frame)、不相邻两帧(late fusion)、相邻多帧(early fusion)以及多阶段相邻多帧(slow fusion)；此外提出了一种多分辨率的网络结构，大大提升了神经网络应用于大规模数据时的训练速度。该模型在Sports-1M上的分类准确率达63.9%，相比于基于人工特征的方法(55.3%)，有很大提升。此外，该模型表现出较好的泛化能力，单独使用slow fusion融合方法所得模型在UCF-101动作识别数据集上的识别率为65.4%，而该数据集的基准识别率为43.9%。

S. Ji等提出一个三维卷积神经网络模型用于行为识别。该模型通过在空间和时序上运用三维卷积提取特征，从而获得多个相邻帧间的运动信息。该模型基于输入帧生成多个特征图通道，将所有通道的信息结合获得最后的特征表示。该三维卷积神经网络模型在TRECVID数据上优于其他方法，表明该方法对于真实环境数据有较好的效果；该模型在KTH数据上的表现，逊于其他方法，原因是为了简化计算而缩小了输入数据的分辨率。

M. Baccouche等提出一种时序的深度学习模型，可在没有任何先验知识的前提下，学习分类人体行为。模型的第一步，是将卷积神经网络拓展到三维，自动学习时空特征。接下来使用RNN方法训练分类每个序列。该模型在KTH上的测试结果优于其他已知深度模型，KTH1和KTH2上的精度分别为94.39%和92.17%。

七、 深度学习存在的问题及未来研究方向

1、 深度学习目前存在的问题：

(1)、理论问题：

深度学习在理论方面存在的困难主要有两个，第一个是关于统计学习，另一个和计算量相关。相对浅层学习模型来说，深度学习模型对非线性函数的表示能力更好。根据通用的神经网络逼近理论，对任何一个非线性函数来说，都可以由一个浅层模型和一个深度学习模型很好的表示，但相对浅层模型，深度学习模型需要较少的参数。关于深度学习训练的计算复杂度也是我们需要关心的问题，即我们需要多大参数规模和深度的神经网络模型去解决相应的问题，在对构建好的网络进行训练时，需要多少训练样本才能足以使网络满足拟合状态。另外，网络模型训练所需要消耗的计算资源很难预估，对网络的优化技术仍有待进步。由于深度学习模型的代价函数都是非凸的，这也造成理论研究方面的困难。

(2)、建模问题：

在解决深层学习理论和计算困难的同时，如何构建新的分层网络模型，既能够像传统深层模型一样能够有效的抽取数据的潜在特征，又能够像支持向量机一样便于进行理论分析，另外，如何针对不同的应用问题构建合适的深层模型同样是一个很有挑战性的问题。现在用于图像和语言的深度模型都拥有相似卷积和降采样的功能模块，研究人员在声学模型方面也在进行相应的探索，能不能找到一个统一的深度模型适用于图像，语音和自然语言的处理仍需要探索。

(3)、工程应用问题：

在深度学习的工程应用问题上，如何利用现有的大规模并行处理计算平台进行大规模样本数据训练是各个进行深度学习研发公司首要解决的难题。由于像Hadoop这样的传统大数据处理平台的延迟过高，不适用于深度学习的频繁迭代训练过程。现在最多采用的深度网络训练技术是随机梯度下降算法。这种算法不适于在多台计算机间并行运算，即使采用GPU加速技术对深度神经网络模型进行训练也是需要花费漫长的时间。随着互联网行业的高速发展，特别是数据挖掘的需要，往往面对的是海量需要处理的数据。由于深度学习网络训练速度缓慢无法满足互联网应用的需求。

2、 深度学习未来研究方向：

深度学习算法在计算机视觉(图像识别、视频识别等)和语音识别中的应用，尤其是大规模数据集下的应用取得突破性的进展，但仍有以下问题值得进一步研究：

(1)、无标记数据的特征学习

目前，标记数据的特征学习仍然占据主导地位，而真实世界存在着海量的无标记数据，将这些无标记数据逐一添加人工标签，显然是不现实的。所以，随着数据集和存储技术的发展，必将越来越重视对无标记数据的特征学习，以及将无标记数据进行自动添加标签技术的研究。

(2)、模型规模与训练速度

训练精度之间的权衡。一般地，相同数据集下，模型规模越大，训练精度越高，训练速度会越慢。例如一些模型方法采用ReLU非线性变换、GPU运算，在保证精度的前提下，往往需要训练5~7d。虽然离线训练并不影响训练之后模型的应用，但是对于模型优化，诸如模型规模调整、超参数设置、训练时调试等问题，训练时间会严重影响其效率。故而，如何在保证一定的训练精度的前提下，提高训练速度，依然是深度学习方向研究的课题之一。

(3)、理论分析

需要更好地理解深度学习及其模型，进行更加深入的理论研究。深度学习模型的训练为什么那么困难?这仍然是一个开放性问题。一个可能的答案是深度结构神经网络有许多层，每一层由多个非线性神经元组成，使得整个深度结构神经网络的非线性程度更强，减弱了基于梯度的寻优方法的有效性；另一个可能的答案是局部极值的数量和结构随着深度结构神经网络深度的增加而发生定性改变，使得训练模型变得更加困难。造成深度学习训练困难的原因究竟是由于用于深度学习模型的监督训练准则大量存在不好的局部极值，还是因为训练准则对优化算法来说过于复杂，这是值得探讨的问题。此外，对堆栈自编码网络学习中的模型是否有合适的概率解释，能否得到深度学习模型中似然函数梯度的小方差和低偏差估计，能否同时训练所有的深度结构神经网络层，除了重构误差外，是否还存在其他更合适的可供选择的误差指标来控制深度结构神经网络的训练过程，是否存在容易求解的RBM配分函数的近似函数，这些问题还有待未来研究。考虑引入退火重要性抽样来解决局部极值问题，不依赖于配分函数的学习算法也值得尝试。

(4)、数据表示与模型

数据的表示方式对学习性能具有很大的影响，除了局部表示、分布表示和稀疏分布表示外，可以充分利用表示理论研究成果。是否还存在其他形式的数据表示方式，是否可以通过在学习的表示上施加一些形式的稀疏罚从而对RBM和自编码模型的训练性能起到改进作用，以及如何改进。是否可以用便于提取好的表示并且包含更简单优化问题的凸模型代替RBM和自编码模型；不增加隐单元的数量，用非参数形式的能量函数能否提高RBM的容量等，未来还需要进一步探讨这些问题。此外，除了卷积神经网络、DBN和堆栈自编码网络之外，是否还存在其他可以用于有效训练的深度学习模型，有没有可能改变所用的概率模型使训练变得更容易，是否存在其他有效的或者理论上有效的方法学习深度学习模型，这也是未来需要进一步研究的问题。现有的方法，如DBN．HMM和DBN—CRF，在利用DBN的能力方面只是简单的堆栈叠加基本模型，还没有充分发掘出DBN的优势，需要研究DBN的结构特点，充分利用DBN的潜在优势，找到更好的方法建立数据的深度学习模型，可以考虑将现有的社会网络、基因调控网络、结构化建模理论以及稀疏化建模等理论运用其中。

(5)、特征提取

除了高斯–伯努利模型之外，还有哪些模型能用来从特征中提取重要的判别信息，未来需要提出有效的理论指导在每层搜索更加合适的特征提取模型。自编码模型保持了输入的信息，这些信息在后续的训练过程中可能会起到重要作用，未来需要研究用CD训练的RBM是否保持了输入的信息，在没有保持输入信息的情况下如何进行修正。树和图等结构的数据由于大小和结构可变而不容易用向量表示其中包含的信息，如何泛化深度学习模型来表示这些信息，也是未来需要研究的问题。尽管当前的产生式预训练加判别式微调学习策略看起来对许多任务都运行良好，但是在某些语言识别等其他任务中却失败了，对这些任务，产生式预训练阶段的特征提取似乎能很好地描述语音变化，但是包含的信息不足以区分不同的语言，未来需要提出新的学习策略，对这些学习任务提取合适的特征，这可以在很大程度上减小当前深度学习系统所需模型的大小。

(6)、训练与优化求解

为什么随机初始化的深度结构神经网络采用基于梯度的算法训练总是不能成功，产生式预训练方法为什么有效?未来需要研究训练深度结构神经网络的贪婪逐层预训练算法到底在最小化训练数据的似然函数方面结果如何，是否过于贪婪，以及除了贪婪逐层预训练的许多变形和半监督嵌入算法之外，还有什么其他形式的算法能得到深度结构神经网络的局部训练信息。此外，无监督逐层训练过程对训练深度学习模型起到帮助作用，但有实验表明训练仍会陷入局部极值并且无法有效利用数据集中的所有信息，能否提出用于深度学习的更有效的优化策略来突破这种限制，基于连续优化的策略能否用于有效改进深度学习的训练过程，这些问题还需要继续研究。二阶梯度方法和自然梯度方法在理论研究中可证明对训练求解深度学习模型有效，但是这些算法还不是深度结构神经网络优化的标准算法，未来还需要进一步验证和改进这些算法，研究其能否代替微批次随机梯度下降类算法。当前的基于微批次随机梯度优化算法难以在计算机上并行处理，目前最好的解决方法是用GPU来加速学习过程，但是单个机器的GPU无法用于处理大规模语音识别和类似的大型数据集的学习，因此未来需要提出理论上可行的并行学习算法来训练深度学习模型。

(7)、与其他方法的融合

从上述应用实例中可发现，单一的深度学习方法，往往并不能带来最好的效果，通常融合其他方法或多种方法进行平均打分，会带来更高的精确率。因此，深度学习方法与其他方法的融合，具有一定的研究意义。

(8)、研究拓展

当深度模型没有有效的自适应技术，在测试数据集分布不同于训练集分布时，它们很难得到比常用模型更好的性能，因此未来有必要提出用于深度学习模型的自适应技术以及对高维数据具有更强鲁棒性的更先进的算法。目前的深度学习模型训练算法包含许多阶段，而在在线学习场景中一旦进入微调阶段就有可能陷入局部极值，因此目前的算法对于在线学习环境是不可行的。未来需要研究是否存在训练深度学习的完全在线学习过程能够一直具有无监督学习成分。DBN模型很适合半监督学习场景和自教学习场景，当前的深度学习算法如何应用于这些场景并且在性能上优于现有的半监督学习算法，如何结合监督和无监督准则来学习输入的模型表示，是否存在一个深度使得深度学习模型的计算足够接近人类在人工智能任务中表现出的水平，这也是未来需要进一步研究的问题。

八、 深度学习开源软件

目前网上关于深度学习的源代码非常多，主要的项目有

框架名称：Caffe
主要维护方：BVLC
支持的语言：C++/Python/Matlab
GitHub源码地址：https://github.com/BVLC/caffe

框架名称：PyTorch
主要维护方：Facebook
支持的语言：C/C++/Python
GitHub源码地址：https://github.com/pytorch/pytorch

框架名称：Theano
主要维护方：UdeM
支持的语言：Python
GitHub源码地址：https://github.com/Theano/Theano

框架名称：CNTK
主要维护方：Microsoft
支持的语言：C++/Python/C#/.NET/Java/R
GitHub源码地址：https://github.com/Microsoft/CNTK

框架名称：PaddlePaddle
主要维护方：Baidu
支持的语言：C++/Python
GitHub源码地址：https://github.com/PaddlePaddle/Paddle/

框架名称：Deeplearning4j
主要维护方：Eclipse
支持的语言：Java/Scala等
GitHub源码地址：https://github.com/eclipse/deeplearning4j

框架名称：ONNX
主要维护方：Microsoft/ Facebook
支持的语言：Python/R
GitHub源码地址：https://github.com/onnx/onnx

框架选择建议

根据上节图表及优缺点分析，综合考虑开发语言、跨平台开发、文档完善性、支持接口等因素，得到了当前受众最广且网上文献、资料最为完善的两个框架：TensorFlow及Pytorch。其他几种深度学习框架不是开发语言不匹配（DL4J、Kears、Teano），就是投资资源有限或者已不再维护（Caffe&Cafe2、Theano、CNTK……）。

TensorFlow和Pytorch我目前最为活跃的连个深度学习框架。

但是，行业里智能驾驶相关算法一般都是基于c++语言开发的较多，虽然深度学习框架的开发语言和智能驾驶算法的开发语言是相互独立的，考虑到个人学习成本问题，建议直接上C++，学习一门语言就可以满足需求。因此，如果有c++基础的，TensorFlow是最佳选项。另外，相比TensorFlow，Pytorch具有以下优势：

学习成本低，上手快；
动态计算图，数据参数在CPU于GPU之间迁移灵活，提升开发效率。
因此，如果不会C++，虽然TensorFlow在依赖库及部署等方面有一定优势，但是综合考虑学习时间成本（python上手比C++要快很多），如果项目时间较为紧张、预留时间不多的前提下，Pytorch不失为一个优选方案。

国内的很多智能驾驶项目都是基于Apollo这套东西来的，如果项目开发用的是百度Apollo算法，其代码适用性最强的肯定还是百度自己的深度学习框架PaddlePaddle。

综上，建议如下：

有C++语言基础：TensorFlow；
具备python语言基础：Pytorch；
项目算法基于Apollo项目开发：PaddlePaddle。
国内深度学习框架自研之路

2020年上半年，华为Mindspore、旷视MegEngine、腾讯TNN、清华Jittor等数个国产AI框架渐次宣布开源，讨论的热度一直在持续。最近一流科技的OneFlow又首创性地引入Actor模型和SBP机制，以其独特设计引起关注。很多人也开始思考：在已有成熟的开源深度学习框架并拥有完整生态的情况下，中国企业和机构是否有必要再另造一套框架？自研深度学习框架的创新空间又有多大？

近几年，基础技术的“卡脖子”问题逐渐浮出水面。不久前美国政府发布的“芯片禁令”将华为逼到了非常被动的境地。前事不忘后事之师，中国要想发展好新一代的人工智能，通过自主研发来掌握AI底层技术无疑是未雨绸缪的重要举措。因此自研深度学习框架是非常必要的。不过局中人也都知道要超越那些已有的成熟的框架也是很难的，那么出路何在？

虽然很多人认为深度学习框架的融合是时之所趋势，TensorFlow2.0和PyTorch也的确是越来越像了，但实际上深度学习框架的市场是很大的，用户需求也是多样的，这就注定不可能由某个企业、某个产品垄断。就像TensorFlow也曾一家独大，但PyTorch横空出世后迅速形成两强对峙的局面，关键就在于两者设计初衷的差异。TensorFlow面向工业界，侧重推理，在部署上实现了工业级的稳定；PyTorch面向学术界，侧重训练，足够简单易用，能达成快速实现和验证。最终两者在各自面向的领域都确立了王者地位。

差异化可能将是深度学习框架自研之路上的制胜关键。单纯依靠模仿的框架肯定是没有出路的，如何与现存的成熟的深度学习框架区别开来进而打造自身亮点是众多开发团队所要考虑的。PaddlePaddle模型库丰富，MegEngine追求训练推理一体化，Mindspore深耕自动并行的训练能力，OneFlow专注分布式环境下的性能提升……相比“一枝独秀”，“百花齐放”无疑更有利于国内深度学习框架的长足发展。

以上整理的内容主要摘自五篇文章：

1、 《基于深度学习的图像检索研究》，内蒙古大学，硕论，2014

2、 《基于卷积神经网络的深度学习算法与应用研究》，浙江工商大学，硕论，2014

3、 《深度学习研究进展》，计算机应用研究，期刊，2014

4、 《深度学习研究综述》，北京工业大学学报，期刊，2015

5、 《深度学习最新研究进展综述》，中国科技论文在线，期刊，2015