详解停车位检测算法 Vision-Based Parking-Slot Detection: A DCNN-Based Approach and a Large-Scale Benchmark_deepps

本文介绍一篇基于深度学习的停车位检测论文：DeepPS，作者同时公开了数据集ps2.0，工作很扎实，对于入门停车位检测很有帮助，论文发表在 IEEE T-IP 2018。

项目链接为：https://cslinzhang.github.io/deepps/

---

0. Abstract

在自动泊车系统中，如何能准确而高效地检测和定位停车位是一个关键但尚未解决的问题。由于路面材质的多样性、光照条件的变化以及树木产生的阴影等因素，使得基于视觉的停车位检测变得比看上去困难得多。

本文提出了一种新的基于卷积神经网络的停车位检测方法，即 DeepPS。DeepPS的关键步骤有两个：识别输入图像上的所有标记点和对标记点对形成的局部图像进行分类。

其次，为了便于基于视觉的停车位检测研究，建立了大规模的数据集。包括从典型的室内和室外停车场采集的12165张环视图。

---

1. Introduction & Related Work

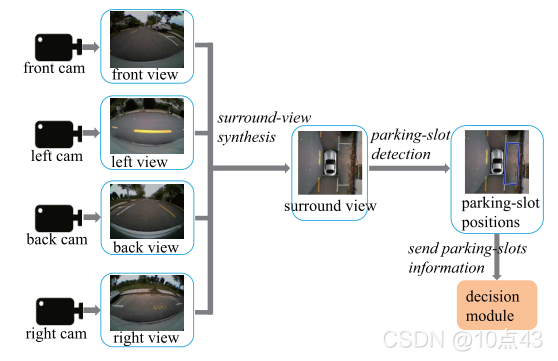
下图是一个典型的基于视觉的停车位检测系统，该系统包括两个模块，即环视图合成和对环视图的停车位检测。（本文重点介绍停车位检测，环视图合成可以查看相关文献。）

下图为本文中收集到的停车位数据：(a)、(b)、( c )、(d)中的停车位是垂直的，(e)、(f)、(g)中的停车位是平行的，(h)中的停车位是倾斜的。(a)和(b)是从室内停车场采集的，其它的是从室外停车场采集的。(b)中的车位线是黄色的，而其它图像中的车位线是白色的。(e)是在雨天采集的，(f)是晚上在路灯下采集的，在(g)中树木造成的阴影覆盖了停车线，(d)和(e)中车位线有所损坏。

对于采集的数据集，作者进行了标注，下图中黄色圆圈为标记点。

---

2. DeepPS: A DCNN-Based Approach

下图分别为理想的垂直、平行和倾斜停车位。在图中，所有标记点都用黄圆圈标记。此外，还标记了车位进入线（有效停车位的两个标记点的连接虚线）和车位分隔线(白色实线)。

对于停车位检测，DeepPS主要分为三步：标记点检测、局部图像模式分类和停车位推理。

---

A. Marking-Point Detection

本文选择YoloV2模型作为标记点检测器。在训练阶段，对于每张环视图，首先人工标注所有的标记点。对于每个标记点 ${\mathbf{p}}_i$，都有一个以标记点为中心固定尺寸为 $p\times p$ 的包围框作为标记点的真值包围框。

为了使检测器具有旋转不变性，作者通过旋转每张原始标记图片来增强训练集。具体地说，每张训练图片 $\mathbf{I}$，可以得到它的 $\mathbf{J}$ 个旋转版本图片， { I j } j = 0 J − 1 \{\mathbf{I}_j\}_{j=0}^{\mathbf{J}-1} {Ij​}j=0J−1​。其中 ${\mathbf{I}}_j$ 经过旋转 $\frac{360}{\mathbf{J}}\times j$ 角度得到。同时标记点的坐标也以同样的方式旋转。

下图中(a)是原始训练图片，(b)是通过将图(a)旋转30度来生成的。标记点为紫色点，边界框为黄色。

---

B. Local Image Pattern Classification

测试时，置信度大于 ${\delta }_1$ 的点将被视为标记点。假如有两个标记点 ${\mathbf{p}}_1,{\mathbf{p}}_2$，还需要验证其是否能够形成有效的车位进入线？

• 首先如果 ${\mathbf{p}}_1,{\mathbf{p}}_2$ 能够形成一个有效的车位进入线，两个标记点之间的距离应该满足一些距离约束条件。如果是平行停车位的车位进入线，应该满足 $t_1<||{\mathbf{p}}_1{\mathbf{p}}_2||<t_2$，如果是垂直或倾斜停车位的车位进入线，应该满足$t_3<||{\mathbf{p}}_1{\mathbf{p}}_2||<t_3$，参数 $t_1、t_2、t_3、t_4$ 是根据各种停车位进入线长度的先验知识确定的。
• 然后，还需要进一步处理满足距离约束的标记点对。首先，对于一对标记点，虽然它可以满足距离约束，但它们仍然很可能无法形成有效的车位进入线。例如，在下面的左图中两个标记点之间的距离满足作为平行停车位的车位进入线的距离约束；然而，这两个标记点仍然无线形成有效的车位进入线，因为它们之间还存在一个标记点未检测出来。另外，假设可以形成有效的车位进入线。还需要确定相关的停车位是在顺时针方向还是在逆时针方向，以及这个停车位是直角还是倾斜。所有这些问题都可以通过将两个标记点形成的局部图像模式分类到预定义的类中来解决。

如中间的图所示：首先建立以 ${\mathbf{p}}_1$ 和 ${\mathbf{p}}_2$ 的中点为原点，以 ${\mathbf{p}}_1{\mathbf{p}}_2$ 为 $\mathbf{X}$ 轴的局部坐标系。因此可以确定它的 $\mathbf{Y}$ 轴。在这个坐标系中，定义了一个矩形区域 $\mathbf{R}$。对于 $\mathbf{R}$，其沿 $\mathbf{X}$ 轴的长度设为 $\Vert {\mathbf{p}}_1{\mathbf{p}}_2\Vert +\Delta x$ 及其沿 $\mathbf{Y}$ 轴的长度设为 $\Delta y$, 从环视图中提取 $\mathbf{R}$ 覆盖的区域，将其归一化为 $w\times h$ 的大小区域，得到了局部图像模式。

在训练阶段，会得到一个由标记点形成的所有局部图像模式组成的集合 $\mathbb{C}$。根据停车位的特征，将集合 $\mathbb{C}$ 中的样本分为7类，如右图所示：逆时针直角，逆时针倾斜（锐角），逆时针倾斜（钝角），顺时针直角，顺时针倾斜(钝角)，顺时针倾斜(锐角)，无效。

在构造集合 $\mathbb{C}$时，还有一个实际问题，类不平衡，这意味着一个特定的类相对于其它类只有很少的实例。为了解决这个问题，作者采用了SMOTE对少数类别进行了过度采样。

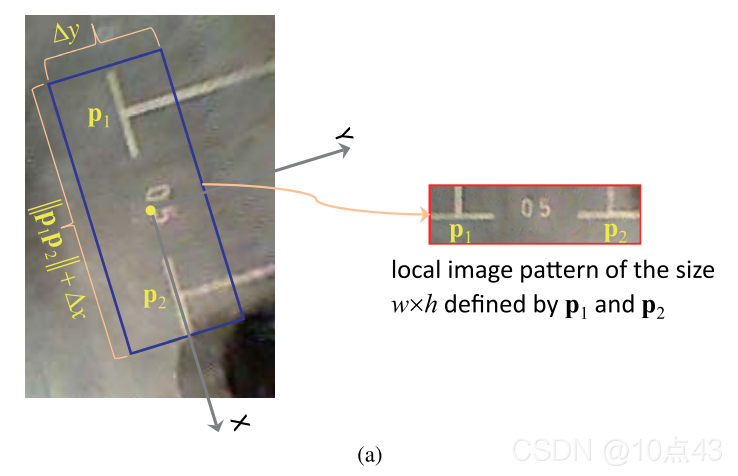作者设计的分类模型如下图所示，右边是模型参数。

---

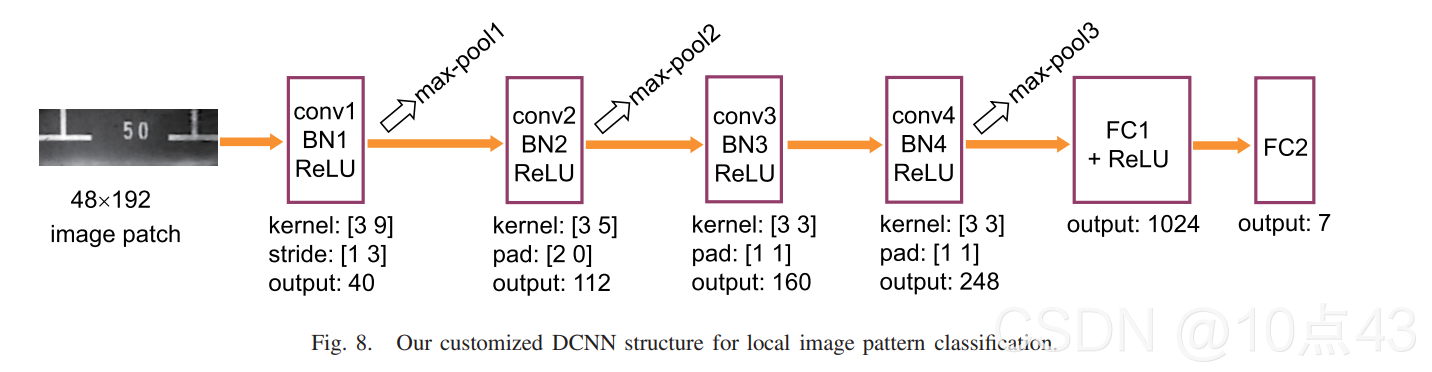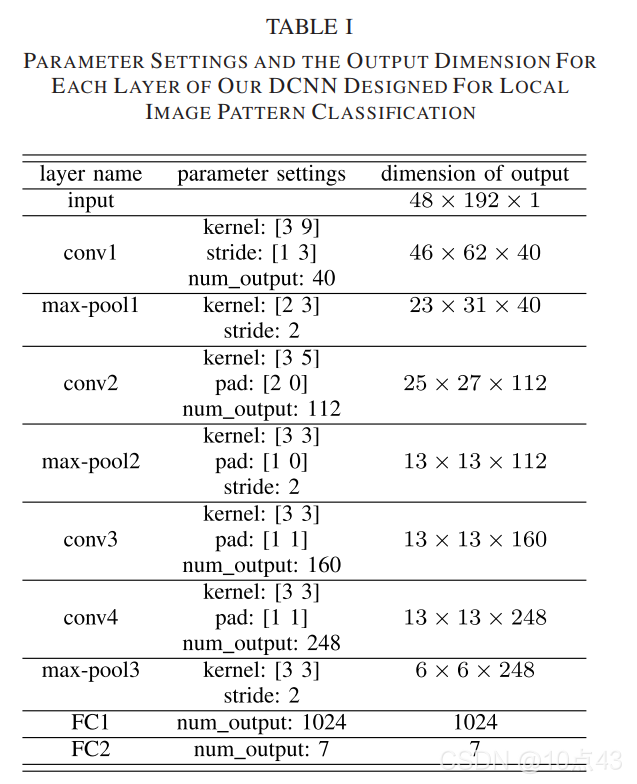C. Parking-Slot Inference

在自动泊车系统中，停车位通常被认为是一个平行四边形，由其四个顶点的坐标表示。在大多数情况下，两个非标记点是不可见的，其坐标只能通过推理得到。为此，需要假设停车位的深度是已知的先验知识。如下图(a)、(b)、( c )所示，垂直、平行和倾斜的停车位的深度分别为 $d_1、d_2、d_3$。

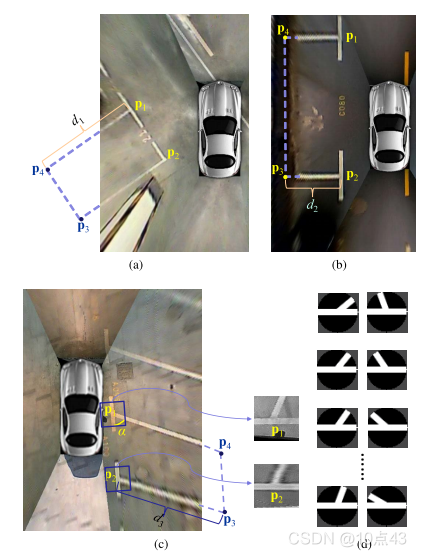
• 假设 ${\mathbf{p}}_1$ 和 ${\mathbf{p}}_2$ 是两个检测到的标记点，形成的局部图像模式分为顺时针直角或逆时针直角，则可以很容易地计算出两个非标记点 ${\mathbf{p}}_3$ 和 ${\mathbf{p}}_4$ 的坐标。例如，在上图(a)中，标记点形成的局部图像模式是顺时针直角并且此停车位应为垂直停车位，其深度为 $d_1$。因此，其另外两个标记点 ${\mathbf{p}}_3$ 和 ${\mathbf{p}}_4$ 可表示为：
  $$\begin{array}{l}{\mathbf{p}}_3=\left[\begin{array}{cc}\cos \frac{\pi }{2}& \sin \frac{\pi }{2}\\ -\sin \frac{\pi }{2}& \cos \frac{\pi }{2}\end{array}\right]\frac{{\mathbf{p}}_1{\mathbf{p}}_2}{\Vert {\mathbf{p}}_1{\mathbf{p}}_2\Vert }\cdot d_1+{\mathbf{p}}_2\\ {\mathbf{p}}_4=\left[\begin{array}{cc}\cos \frac{\pi }{2}& \sin \frac{\pi }{2}\\ -\sin \frac{\pi }{2}& \cos \frac{\pi }{2}\end{array}\right]\frac{{\mathbf{p}}_1{\mathbf{p}}_2}{\Vert {\mathbf{p}}_1{\mathbf{p}}_2\Vert }\cdot d_1+{\mathbf{p}}_1\end{array}$$
• 当由两个标记点形成的局部图像模式被分类为倾斜时，如上图( c )所示。在图( c )中，标记点形成的局部图像模式被分类为逆时针倾斜(锐角)；为了估计两个非标记点的位置，需要估计角度 $\alpha$。为了解决这个问题，采用基于模板匹配的策略。图(d)中所示的是一套理想的T形模板 { T θ j } j = 1 M \{\mathbf{T}_{\theta_j}\}_{j=1}^{M} {Tθj​​}j=1M​，$M$ 是模板数量。每个模板的大小为 $s\times s$。测试时，提取两个标记点的图像进行匹配，则角度 $\alpha$ 为：
  $$\alpha =\underset{{\theta }_j}{\mathrm{argmax}}\left\{{\mathbf{I}}_1\ast {\mathbf{T}}_{{\theta }_j}+{\mathbf{I}}_2\ast {\mathbf{T}}_{{\theta }_j}\right\},j=1,\dots ,M$$
  则其余两个标记点计算为：
  $$\begin{array}{l}{\mathbf{p}}_3=\left[\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\frac{{\mathbf{p}}_1{\mathbf{p}}_2}{\Vert {\mathbf{p}}_1{\mathbf{p}}_2\Vert }\cdot d_3+{\mathbf{p}}_2\\ {\mathbf{p}}_4=\left[\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\frac{{\mathbf{p}}_1{\mathbf{p}}_2}{\Vert {\mathbf{p}}_1{\mathbf{p}}_2\Vert }\cdot d_3+{\mathbf{p}}_1\end{array}$$

最终，DeepPS的训练和测试工作流程如下：

---

3. Experimental Results

A. Benchmark Dataset & Settings

首先介绍数据集：每张环视图的分辨率为600×600，对应于一个10m×10m的区域，即环视图上1个像素的长度对应于物理地面上1.67cm长度。通过离线标定，可以得到从环视图坐标系到以车辆为中心的世界坐标系的变换矩阵。因此，当在环视图上检测到停车位时，可以反投影确定其在世界坐标系中的坐标。

表3和4是 ps1.0，ps2.0 数据集的比较与测试集数据采样分布，表5是超参数设置。

---

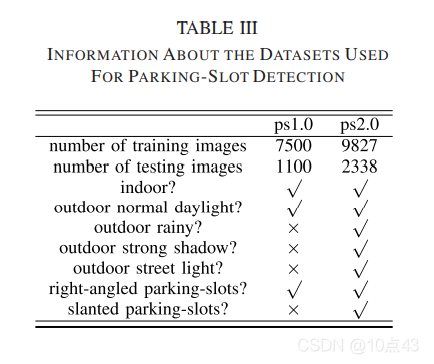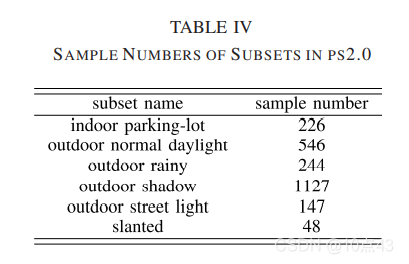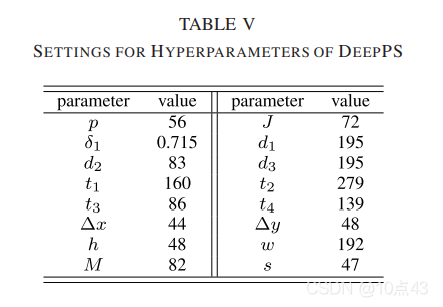B. Marking-Point Detection & Local Image Pattern Classification

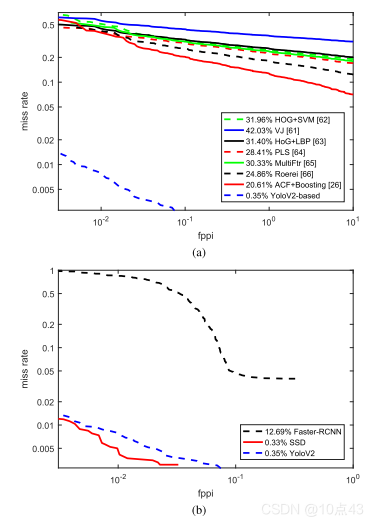
下面介绍标记点检测，对于标记点真值 ${\mathbf{g}}_i$，如果一个检测到的标记点 ${\mathbf{d}}_i$ 满足 $\Vert {\mathbf{g}}_i-{\mathbf{d}}_i\Vert <{\delta }_2$，则认为 ${\mathbf{g}}_i$ 是正确检测的。为了比较不同的检测器，我们通过改变检测置信度的阈值，画出log-log图绘制漏检率与每张图片的误报率。

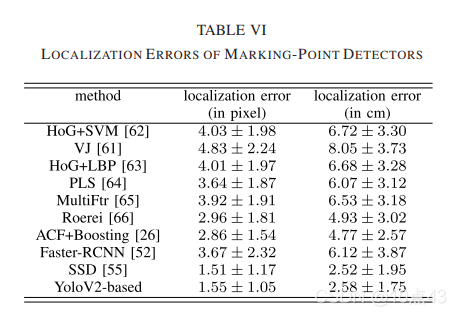
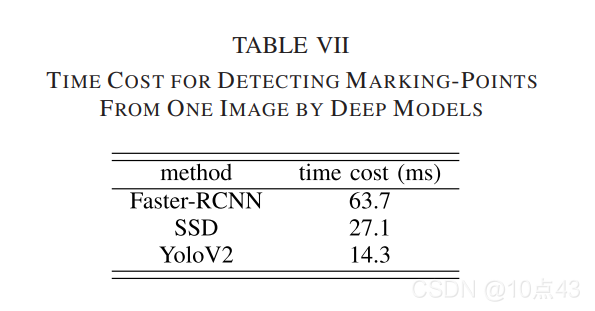
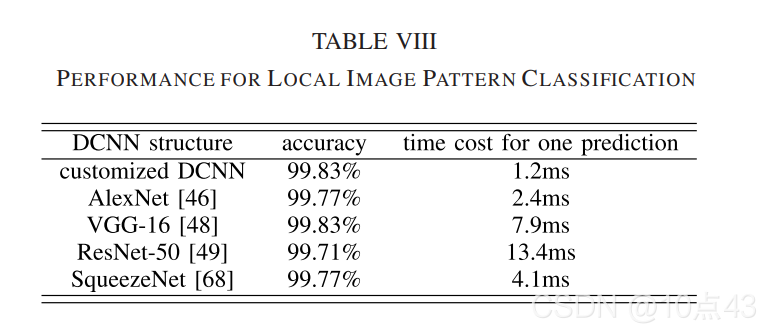
然后是定位误差，用 ${\mathbf{g}}_i$ 表示真值，${\mathbf{g}}_i^{{}^{\prime }}$ 表示检测到的标记点（真阳性）。用 $e_i=\Vert {\mathbf{g}}_i^{\prime }-{\mathbf{g}}_i\Vert$ 表示定位误差，这里使用平均定位误差作为定位误差。漏检率与误报率、定位误差、检测时间比较、局部图案分类结果如下表：

---

C.Parking-Slot Detection

作者与其它几种停车位检测算法进行了比较，结果如下：
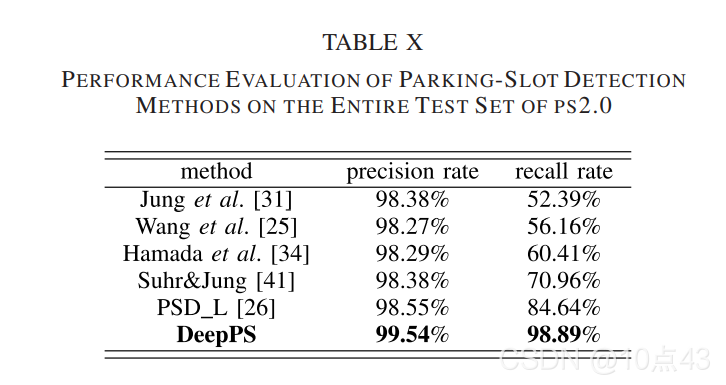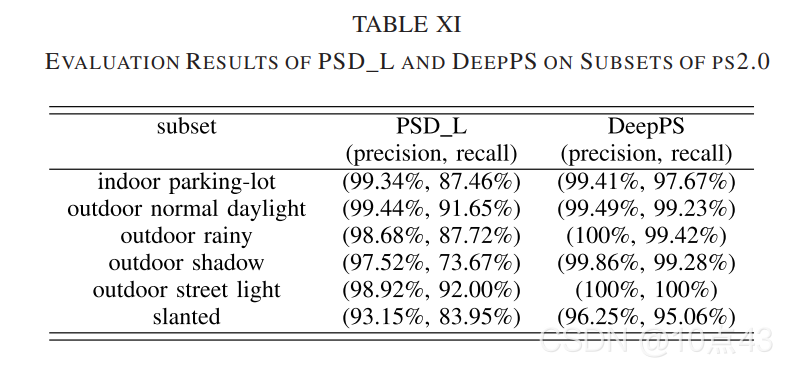