热门标签
热门文章
- 1【Unity3D_常用模块】 Socket网络模块(超级详细完整,上线项目中稳定使用着)_【unity3d_常用模块】 socket网络模块(超级详细完整,上线项目中稳定使用着)
- 2English trip V2-B 24 Biographies Teacher: TAALAN
- 3使用kindeditor直接粘贴本地图片或者是qq截图_营销zz3yswononyon
- 420个优秀免费开源的WEB前端UI框架提高网站开发效率_web ui框架
- 5Day19_多线程(相关概念,另行创建和启动线程,Thread类,线程安全,等待唤醒机制,面试题)
- 6MATLAB小白入门(初级)_菜鸟教程matlab
- 7【Unity】 2D贪吃豆开发流程_unity2d吃豆豆游戏向上碰撞物体,不能销毁
- 8大气模型软件:WRF、CMAQ、SMOKE、MCM、CAMx、Calpuff、人工智能气象、WRFchem、PMF、FLEXPART拉格朗日粒子扩散、WRF-UCM、EKMA_wrf属于统计模型吗
- 9Zabbix 监控ESXi服务器【非虚拟机】CPU、内存、硬盘、网络带宽
- 10ESP8266-01S(ESP-01S)相关资料记录_esp01s原理图
当前位置: article > 正文
主成分分析(Principal Component Analysis,PCA)_extraction method:princplal component analysis.^--
作者:知新_RL | 2024-02-21 23:20:47
赞
踩
extraction method:princplal component analysis.^---^由相关阵出发求主成分
主成分分析(Principal Component Analysis,PCA)是一种常用的降维方法,适用于数据集中特征维度较高的情况。PCA的目的是通过对数据进行线性变换,将原始特征投影到新的低维度空间中,从而实现降维的效果。
PCA的基本原理如下:
-
数据标准化:首先对原始数据进行标准化处理,即将每个特征缩放到零均值和单位方差。这是为了确保每个特征对主成分分析的贡献度均衡。

-
协方差矩阵计算:通过计算原始数据的协方差矩阵来衡量特征之间的相关性。协方差矩阵是一个对称矩阵,其元素为各个特征之间的协方差。
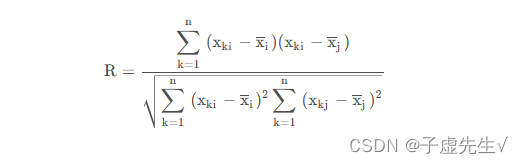
-
特征值分解:对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。特征值表示了特征向量所对应的主成分的重要程度,特征向量表示了原始特征在主成分上的投影。

-
特征值排序:将特征值按照大小进行排序,选择其中最大的k个特征值所对应的特征向量。这k个特征向量构成了新的低维特征空间。

-
数据投影:将原始数据投影到选取的特征向量上,得到降维后的数据。这些新的特征向量是原始特征的线性组合,也称为主成分。
通过PCA降维,可以达到减少数据特征维度、去除冗余信息、提高计算效率等目的。同时,主成分的选择也是根据特征值的大小,选取最具有代表性和区分性的特征,可以更好地反映数据的结构和特征。
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/知新_RL/article/detail/127228
推荐阅读
相关标签


