【机器学习/人工智能】 实验一：典型监督学习方法分类实践与比较分析_基于机器学习的分类实验对比

一、实验目的与要求

(1)利用所学习的监督学习方法完成目标识别实验方案的设计。
(2)编程并利用相关软件完成实验测试，得到实验结果。
(3)通过对实验数据的分析﹑整理，方法的对比，得出实验结论，培养学生创新思维和编写实验报告的能力，以及处理一般工程设计技术问题的初步能力及实事求是的科学态度。
(4)利用实验更加直观﹑方便和易于操作的优势，提高学生学习兴趣，让学生自主发挥设计和实施实验，发挥出学生潜在的积极性和创造性。

二、实验内容

(1)采用已经学过的监督学习的方法，如逻辑回归、决策树、神经网络等实现分类任务。
(2)分析比较不同方法的优缺点。

三、实验设备与环境

Windows11系统、Anaconda3、Pycharm Community、Jupyter Notebook、Scikit-learn库

四、设计正文

（包括分析与设计思路、各模块流程图以及带注释的主要算法源码，若有改进或者创新，请描述清楚，并在实验结果分析中对比改进前后的结果并进行分析）

4.1 分析与设计思路

逻辑回归的基础是线性回归。线性模型试图学习一个通过属性的线性组合进行预测的函数，用向量形式写作$f(\vec{x})=\overrightarrow{w^T}\vec{x}+b$，学习合适的$\overrightarrow{w^T}$和$b$值，使得目标函数$J(\vec{w},b)={\sum }_{i=1}^{m}f({\vec{x}}_i-y_i{)}^2$最小。可以使用线性回归或梯度下降法得到$\vec{w}$和$b$值。
逻辑回归在线性回归的基础上，使用一个Sigmoid函数作为预测分类函数。Sigmoid函数公式为$\varphi (z)=\frac{1}{1+e^{-z}}$。将$f(\vec{x})$代入$z$，得到$h_{\theta }(\vec{x})=\frac{1}{1+e^{-f(\vec{x})}}$，其中$h_{\theta }(x)$表示函数概率值，即结果为1的概率。对于输入$\vec{x}$,分类属于类别1和类别0的概率分别为$h_{\theta }(x)$和$1-h_{\theta }(x)$。逻辑回归的损失函数采用对数损失函数。
$$L(\hat{y},y)=-[y{\log }_2\hat{y}+(1-y){\log }_2(1-\hat{y})]$$
利用梯度下降的办法对参数$\overrightarrow{w^T}$和$b$进行更新的公式如下：
$$\begin{gathered} \overrightarrow{w^T}\leftarrow \overrightarrow{w^T}-\alpha [\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}(\overrightarrow{x^{(i)})-y^{(i)}})x_j^{(i)}] \\ b\leftarrow b-\alpha [\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}(\overrightarrow{x^{(i)})-y^{(i)}})] \end{gathered}$$

对逻辑回归的效果评估，一般采用AUC曲线下面积指标进行评价。
逻辑回归的流程图如图所示。

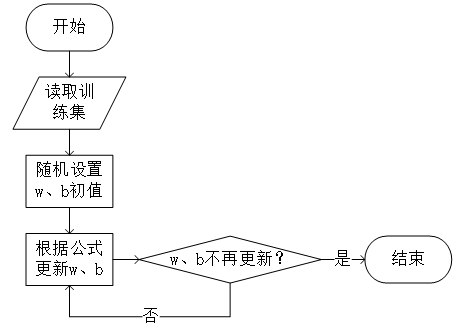
决策树把数据样本分配到叶子结点确定数据集中样本所属的分类。决策结点表示在样本的一个属性上进行的划分，叶结点表示经过分支到达的类。从根结点出发，每个决策结点进行一次划分，到达叶子结点得到最终的分类结果。
ID3算法在每个结点选取能获取最高信息增益的分支属性进行分裂。设样本集合$S$的大小为$n$，其分类属性有$m$个不同取值，将样本集分为$C_i(i=1,2,...,n)$,则信息熵计算公式为
$$Ent(S)=-\sum _{i=1}^m{p}_i{\log }_2(p_i),p_i=\frac{|C_i|}{|n|}$$
得到了信息熵后，对于样本集$S$，计算以属性$A$为分支属性的信息增益$Gain(S,A)$，其公式为
$$Gain(S,A)=Ent(S)-\sum _{i=1}^v\frac{|S_i|}{|S|}Ent(S_i)$$
不断重复以上分裂过程，直到满足以下几个条件之一时，停止分裂生长：样本中的所有数据属于同一标签、已达最大深度、结点中样本数小于某阈值、信息增益小于某阈值（防止过拟合）。
因此，决策树的整体流程如下图所示。

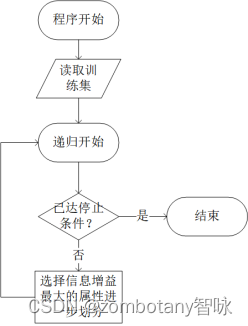
神经网络最基本的成分是神经元，神经元接受多个输入，并利用激活函数输出作为整个神经网络的输出或多层感知机中下一层网络的输入。
最简单的神经网络模型就是简单感知机，感知机是二分类模型。输入为特征向量$\vec{x}$，输出为实例$y=g(\vec{w}\cdot \vec{x}+b)$。其中$g(z)$为激励函数。Loss函数可以使用误分类点到超平面的距离，即$\frac{1}{||w||}|\vec{w}\cdot \vec{x}+b|$。对于误分类点$(x_i,y_i)$，有$-y_i(w\cdot x_i+b)>0$成立。所有误分类点到超平面总距离$\frac{1}{||w||}{\sum }_{x_i\in M}{y}_i(\vec{w}\cdot {\vec{x}}_i+b)$。误分类点总数为$L(w,b)=-{\sum }_{x_i\in M}{y}_i(\vec{w}\cdot {\vec{x}}_i+b)$
利用梯度下降法进行迭代
$${\theta }^{\prime }=\theta -\eta {\nabla }_{\theta }L(\theta ),\frac{\partial L(\theta )}{\partial w}=-\sum _{x_i\in M}{y}_i{x}_i,\frac{\partial L(\theta )}{\partial b}=-\sum _{x_i\in M}{y}_i$$
所以对于误分类点，更新$\vec{w}$和$b$，${\vec{w}}^{\prime }=\vec{w}+\eta y_i{x}_i,b^{\prime }=b+\eta y_i$
整体流程如下图所示。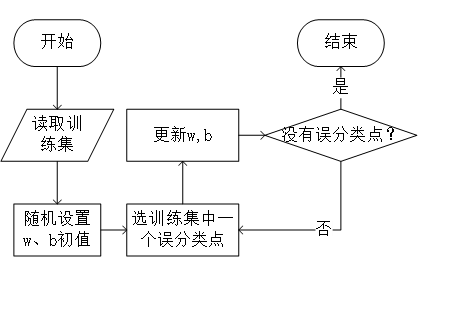
在测试各类算法时，需要先读取数据集，将数据集分为训练集与测试集。训练模型，并用模型对测试集数据进行预测，将预测值与真实值比对，得到accuracy值。将预测结果与训练数据的切片绘散点图输出。

4.2 主要算法源码

逻辑回归算法代码如下：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.metrics import plot_confusion_matrix
from mlxtend.plotting import plot_decision_regions
from sklearn import metrics
iris = load_iris()#加载数据集
x_train,x_test,y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3)#分割数据集
lr = LogisticRegression()#逻辑回归
lr.fit(x_train, y_train)#训练模型

y_pred = lr.predict(x_test)#用模型预测
print('The accuracy of the Logistic Regression is',metrics.accuracy_score(y_pred,y_test))
matrix = plot_confusion_matrix(lr, x_test, y_test,
                                 cmap=plt.cm.Blues,
                                 normalize='true')
plt.title('Confusion matrix for our classifier')
plt.show()#输出混淆矩阵
plt.figure(1, figsize=(8, 6))
#绘制散点图
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='r',marker='+',label='A型')
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='g',marker='+',label='B型')
plt.scatter(x_train[y_train==2,0],x_train[y_train==2,1],color='b',marker='+',label='C型')

plt.scatter(x_test[y_pred==0,0],x_test[y_pred==0,1],color='r',label='A型')
plt.scatter(x_test[y_pred==1,0],x_test[y_pred==1,1],color='g',label='B型')
plt.scatter(x_test[y_pred==2,0],x_test[y_pred==2,1],color='b',label='C型')
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

决策树算法代码如下：

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn import tree      # 导入scikit-learn的tree模块
from sklearn.model_selection import train_test_split
from sklearn.metrics import plot_confusion_matrix
import graphviz
from sklearn import metrics
iris = load_iris()#加载数据集
x_train,x_test,y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3)#分割数据集
model = tree.DecisionTreeClassifier(criterion='entropy',max_depth=3)#信息熵增益，最大深度为3
model.fit(x_train, y_train)#训练模型

y_pred = model.predict(x_test)#用模型预测
print('The accuracy of the Logistic Regression is',metrics.accuracy_score(y_pred,y_test))
matrix = plot_confusion_matrix(model, x_test, y_test,
                                 cmap=plt.cm.Blues,
                                 normalize='true')
plt.title('Confusion matrix for our classifier')
plt.show()#输出混淆矩阵
plt.figure(1, figsize=(8, 6))
#绘制散点图
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='r',marker='+',label='A型')
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='g',marker='+',label='B型')
plt.scatter(x_train[y_train==2,0],x_train[y_train==2,1],color='b',marker='+',label='C型')

plt.scatter(x_test[y_pred==0,0],x_test[y_pred==0,1],color='r',label='A型')
plt.scatter(x_test[y_pred==1,0],x_test[y_pred==1,1],color='g',label='B型')
plt.scatter(x_test[y_pred==2,0],x_test[y_pred==2,1],color='b',label='C型')
plt.show()

#输出决策树
dot_data=tree.export_graphviz(model)
graph = graphviz.Source(dot_data)
graph.render("decisiontree")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

神经网络算法代码如下：

from sklearn import datasets
from sklearn.datasets import load_iris
import tensorflow as tf
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
iris = load_iris()#加载数据集
x_train,x_test,y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)#分割数据集
w = tf.Variable(tf.random.truncated_normal([4,3],seed=1,stddev=0.1))#随机初始值
b = tf.Variable(tf.random.truncated_normal([  3],seed=1,stddev=0.1))#随机初始值
x_train = tf.cast(x_train,dtype=tf.float32)
x_test  = tf.cast(x_test ,dtype=tf.float32)
train=tf.data.Dataset.from_tensor_slices((x_train,y_train)).batch(32)#batch
test =tf.data.Dataset.from_tensor_slices((x_test, y_test )).batch(32)
epochs=200
alpha=0.2#学习率
history_error=[]#历史损失函数error
history_acc=[]#历史准确率
for _ in range(epochs):
    sumerror=0
    for(x,y) in train:
        with tf.GradientTape() as tape:
            forward_propagation=tf.matmul(x,w)+b#前向传播结果
            forward_propagation=tf.nn.softmax(forward_propagation)#激活前向传播结果
            label_onehot=tf.one_hot(y,depth=3,dtype=tf.float32)#将y转变为onehot编码
            error=tf.reduce_mean(tf.square(label_onehot-forward_propagation))#loss函数
            sumerror+=error.numpy()
        error_grad=tape.gradient(error,[w,b])
        w.assign(w-alpha*error_grad[0])#更新wb
        b.assign(b-alpha*error_grad[1])
    print("train set:epoch:%d error:%f"%(_,sumerror/4))
    truesum=0#总正确数
    testsum=0#测试总数
    for (x,y) in test:
        forward_propagation=tf.matmul(x,w)+b
        forward_propagation=tf.nn.softmax(forward_propagation)
        label=tf.cast(tf.argmax(forward_propagation,axis=1),dtype=y.dtype)
        isaccurate=tf.cast(tf.equal(label,y),dtype=tf.int32)#判断结果
        true=tf.reduce_sum(isaccurate)#正确数
        testsum+=x.shape[0]#测试总数
        truesum+=int(true)#总正确数
    print("test  set:epoch:%d error:%f accuracy:%f"%(_,sumerror/4,truesum/testsum))
    history_error.append(sumerror)
    history_acc.append(truesum/testsum)
plt.title("Loss")
plt.xlabel("Epoch")
plt.ylabel("loss")
plt.plot(history_error)
plt.show()

plt.title("Acc")
plt.xlabel("Epoch")
plt.ylabel("acc")
plt.plot(history_acc)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

五、实验结果及分析

逻辑回归运行结果如下，训练集数据点用+号表示，测试集数据点用默认的圆表示。

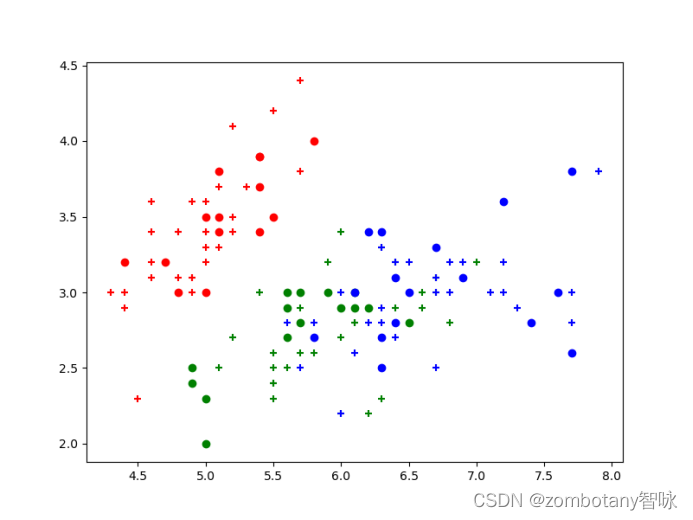
其准确率为0.97，混淆矩阵如下。

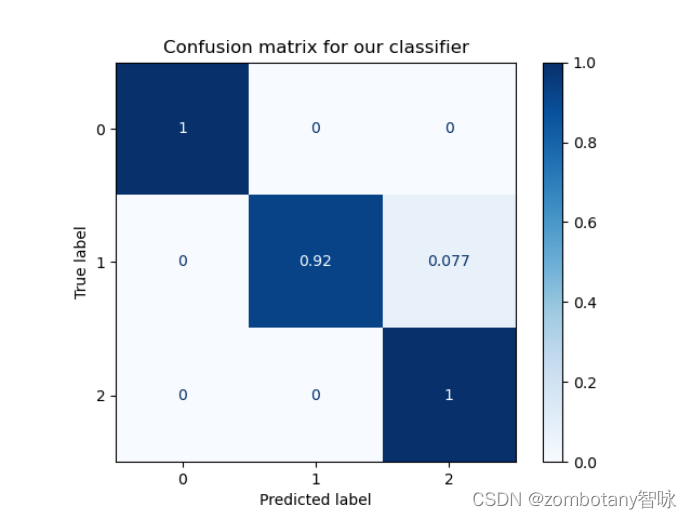
决策树运行结果如下，训练集数据点用+号表示，测试集数据点用默认的圆表示。

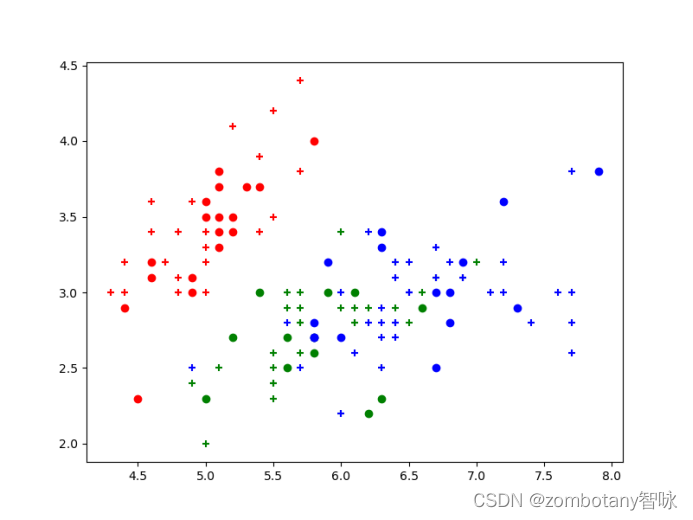
其准确率为0.91，混淆矩阵如下。

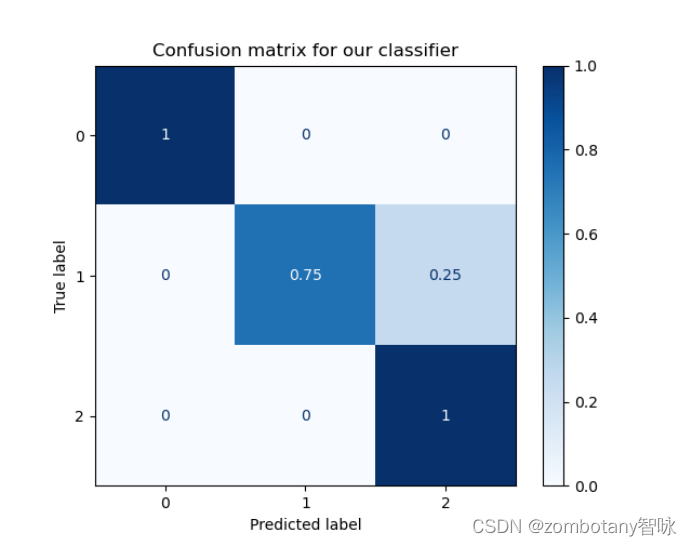
可以对决策树进行可视化，可视化结果如下。决策树采用信息增益算法，最大深度为3。

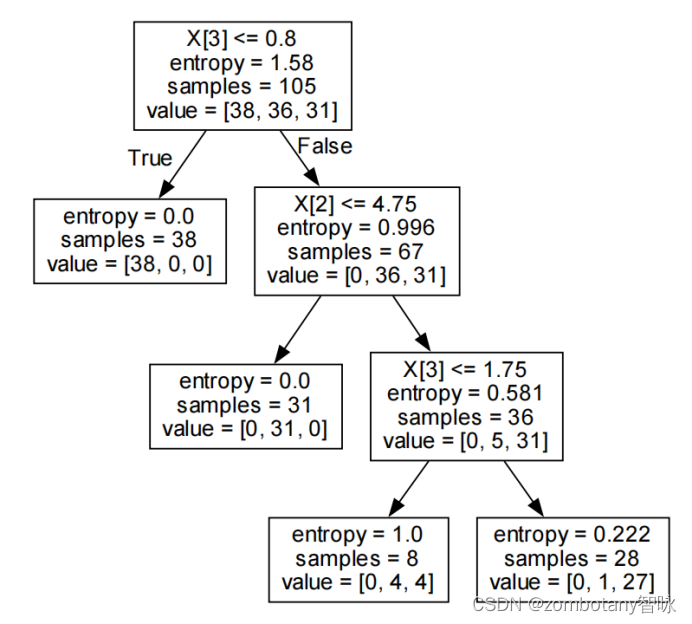
神经网络是黑盒，但可以看到损失函数的曲线收敛的过程、准确性逐渐提升的过程如下。


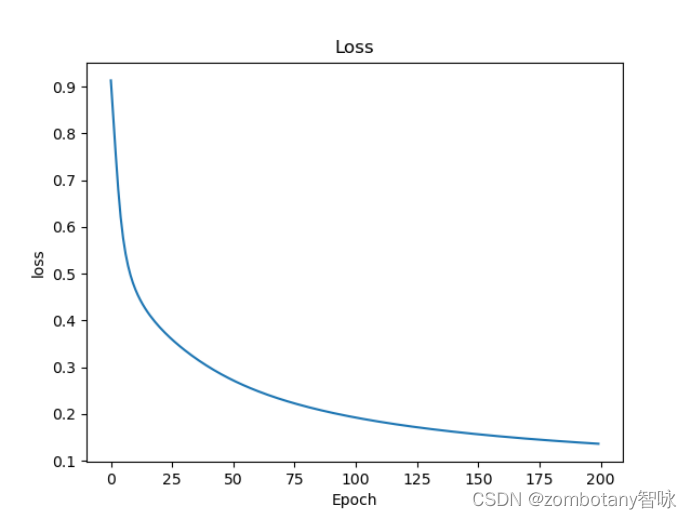
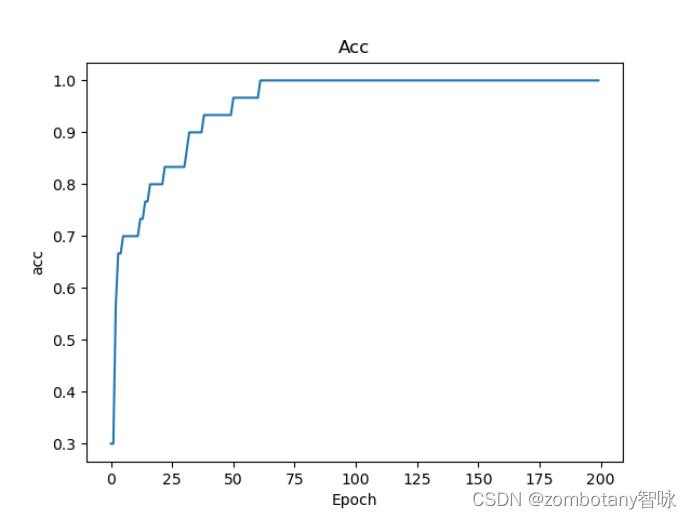
逻辑回归算法的优点是训练速度较快，适合二分类问题，不需要缩放输入特征，可解释性好。缺点是对于非结构化的数据难以自动识别、提取特征。因为模型本身很简单，所以会造成欠拟合等问题，导致模型的准确率不高。
决策树算法的优点是可解释性强，可以很好地处理离散或连续的结构化数据，运行速度快。缺点是容易发生过拟合。
基础神经网络算法的优点是准确率高，可以自动学习各种特征的权重值。缺点是可解释性差，容易发生过拟合，且耗时长。