RC低通滤波器截止频率公式推导_rc低通滤波电路

一阶RC低通滤波器

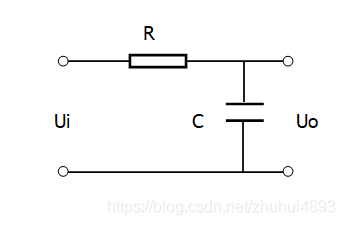
一阶RC滤波器如图所示，电阻$R$串联电容$C$，输入电压记为$U_i$，输出电压记为$U_o$，电容容抗记为$X_c=\frac{1}{j\omega c}$，

根据串联分压，列出传递函数，
$$H(j\omega )=\frac{U_o}{U_i}=\frac{X_c}{R+X_c}=\frac{\frac{1}{j\omega c}}{R+\frac{1}{j\omega c}}=\frac{1}{1+j\omega RC}$$
复数为分母，实数为分子，不方便我们后续计算复向量的模，这里做一下简单的变换，给出变换的过程。
假设有复数$Z=a+bj$，则倒数为$\frac{1}{Z}=\frac{1}{a+bj}$，分子分母同乘以$a-bj$，即有，
$$\frac{1}{Z}=\frac{a-bj}{(a+bj)(a-bj)}=\frac{a-bj}{a^2+b^2}$$
带入可得，
$$H(j\omega )=\frac{U_o}{U_i}=\frac{1-j\omega RC}{1+(\omega RC{)}^2}$$

计算该复数的模，则有，
$$|H(j\omega )|=\sqrt{(\frac{1}{1+(\omega RC{)}^2}{)}^2+(\frac{\omega RC}{1+(\omega RC{)}^2}{)}^2}=\sqrt{\frac{1}{1+(\omega RC{)}^2}}$$
复数的模代表了电压增益，当电压增益下降到$\frac{\sqrt{2}}{2}$倍时，此时的频率即为截止频率，记为$f_c$，那么就有，
$$|H(j\omega )|=\sqrt{\frac{1}{1+(\omega RC{)}^2}}=\frac{\sqrt{2}}{2}$$
化简可得，
$$\omega RC=1=2\pi f_{c}RC$$
求得截止频率$f_c$，
$$f_c=\frac{1}{2\pi RC}$$

二阶RC低通滤波器

二阶RC滤波器如图所示，可见由两个一阶电路构成。第一个一阶电路的电阻记为$R1$，电容记为$C1$；第二个一阶电路的电阻记为$R2$，电容记为$C2$，，输入电压记为$U_i$，输出电压记为$U_o$，电容容抗记为$X_c=\frac{1}{j\omega c}$（这里便于分析，取电阻$R1=R2=R$，电容$C1=C2=C$）。

二阶电路的分析比一阶稍繁琐，不过原理还是一样，输出电压$U_o$即为电容$C2$上的压降，电容C2上的压降来自于电容$C1$上压降的分压。

梳理完电路结构，列出传递函数，
$$H(j\omega )=\frac{U_o}{U_i}=\frac{X_c//(R+X_c)}{R+X_c//(R+X_c)}\frac{X_c}{R+X_c}$$
化简可得，
$$H(j\omega )=\frac{j\omega RC+1}{(j\omega RC{)}^2+3j\omega RC+1}\frac{1}{j\omega RC+1}=\frac{1}{1-(\omega RC{)}^2+3j\omega RC}$$
计算该复数的模，
$$|H(j\omega )|=\sqrt{\frac{1}{(1-(\omega RC{)}^2{)}^2+9(\omega RC{)}^2}}$$
令$|H(j\omega )|=\frac{\sqrt{2}}{2}$，解得，
$$\omega =\frac{1}{2.672RC}$$
求得截止频率$f_c$，
$$f_c=\frac{1}{5.344\pi RC}$$