PTA-6-2 是否二叉搜索树 (25 分)_是否二叉搜索树 分数 25 作者 ds课程组 单位 浙江大学 本题要求实现函数,判断给定

本题要求实现函数，判断给定二叉树是否二叉搜索树。

函数接口定义：

bool IsBST ( BinTree T );
1

其中BinTree结构定义如下：

typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};
1
2
3
4
5
6
7

函数IsBST须判断给定的T是否二叉搜索树，即满足如下定义的二叉树：

定义：一个二叉搜索树是一棵二叉树，它可以为空。如果不为空，它将满足以下性质：

• 非空左子树的所有键值小于其根结点的键值。
• 非空右子树的所有键值大于其根结点的键值。
• 左、右子树都是二叉搜索树。

如果T是二叉搜索树，则函数返回true，否则返回false。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef enum { false, true } bool;
typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

BinTree BuildTree(); /* 由裁判实现，细节不表 */
bool IsBST ( BinTree T );

int main()
{
    BinTree T;

    T = BuildTree();
    if ( IsBST(T) ) printf("Yes\n");
    else printf("No\n");

    return 0;
}
/* 你的代码将被嵌在这里 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

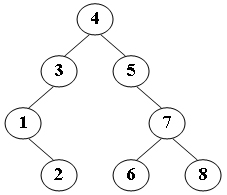
输入样例1：如下图

输出样例1：

Yes
1

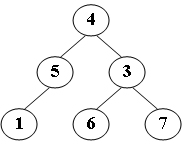
输入样例2：如下图

输出样例2：

No
1

作者: DS课程组

单位: 浙江大学

时间限制: 400ms

内存限制: 64MB

代码长度限制: 16KB

这道题就是个坑，坑死个人。注意，除开他说的这些条件，一个二叉搜索树还应该满足，左子树的最右边<根节点<右子树的最左边

代码如下：

bool IsBST ( BinTree T )
{
    if(!T)
    {
        return true;
    }
    else
    {
        if(IsBST(T->Left)&&IsBST(T->Right))
        {
            BinTree p,q;
            p=T->Left;
            q=T->Right;
            while(p&&p->Right)
            {
                p=p->Right;
            }
            while(q&&q->Left)
            {
                q=q->Left;
            }
            if(T->Left&&T->Right)
            {
               
                if(T->Data>T->Left->Data&&T->Right->Data>T->Data)
                {
                    if(p->Data<T->Data&&q->Data>T->Data)
                        return true;
                    else
                        return false;
                }  
                else
                    return false;
            }
            if(T->Left||T->Right)
            {
                if(!T->Left)
                {
                    if(T->Right->Data<T->Data)
                    {
                        return false;
                    }
                    else
                        return true;
                }
                else if(!T->Right)
                {
                   
                    if(T->Left->Data>T->Data)
                    {
                        return false;
                    }
                    else
                        return true;
                }
            } 
        }
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60