由给定的二叉树存储结构创建其顺序存储结构_数据结构与算法：15 树

15 树

知识结构：

---

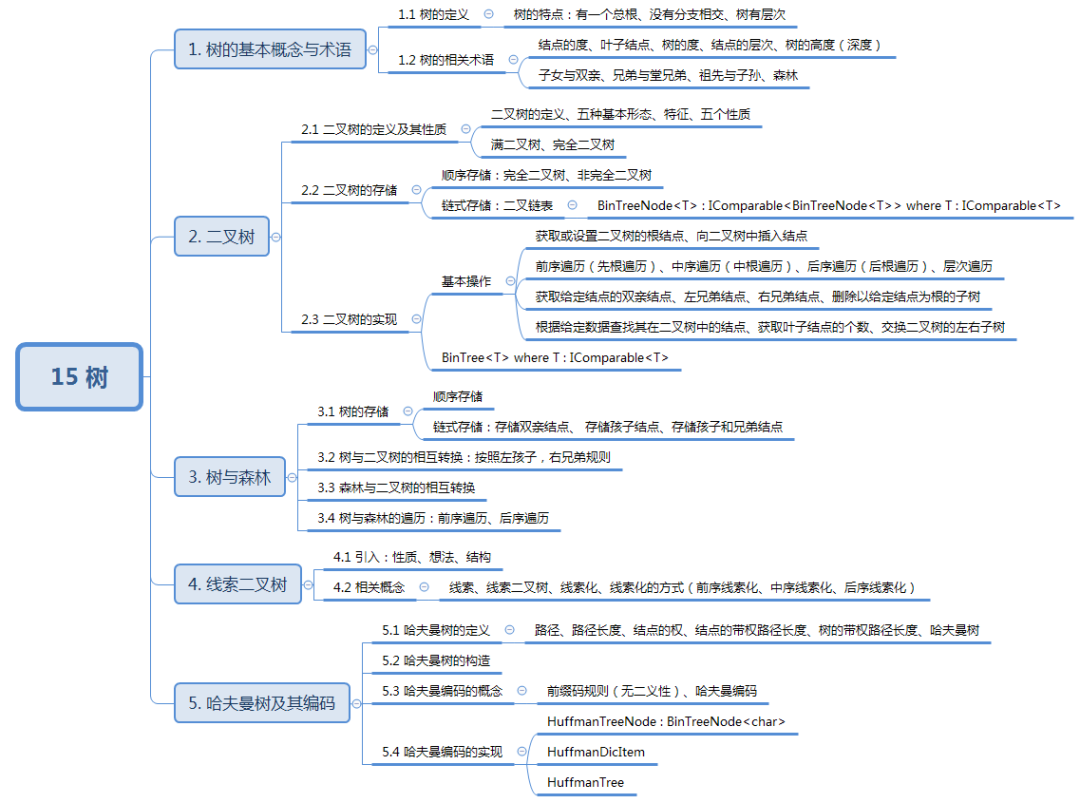
1. 树的基本概念与术语

1.1 树的定义

树是个结点组成的有穷集合 ，该集合具有如下特征：

(1)除的树外，有且仅有一个特定的称为根的结点。

(2)其余结点分为个互不相交的有穷集合，其中每一个集合都是一棵树，称为该根的子树。

例：

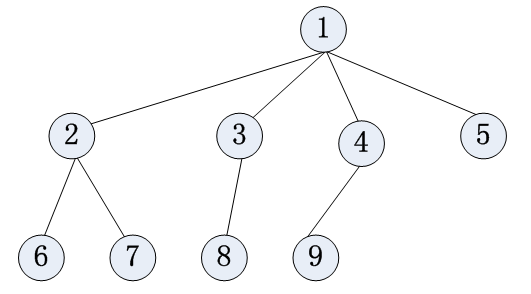
树的特点：

(1)有一个总根。

(2)没有分支相交。

(3)树有层次。

1.2 树的相关术语

结点的度：该结点具有子树的数目。

叶子结点：度为零的结点。(没有子树的结点)

树的度：树中结点度的最大值。

子女与双亲：子女指该结点子树的根结点，双亲即该结点。

结点的层次(Level)：根到该结点的路径长度。(根为第零层、若结点在层，则其子女在层)。

树的高度(深度)：树中结点层的最大值。

兄弟与堂兄弟：同一双亲孩子之间称为兄弟，其双亲在同一层的结点互为堂兄弟。

祖先与子孙：从根到该结点所经分支上的所有结点称为该结点的祖先，以该结点为根的子树中的所有结点称为该结点的子孙。

森林：棵互不相交的树的集合。

---

2. 二叉树

2.1 二叉树的定义及其性质

(1)二叉树的定义

二叉树是结点的有穷集合，且必须满足下面的条件之一：

• 它是空集。
• 它由一个根结点和其左右子树构成且其左右子树满足二叉树的定义。

(2)二叉树的基本形态

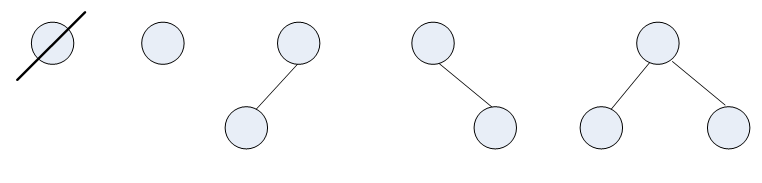
(3)二叉树的特征

• 二叉树的每个结点的度不大于2。
• 二叉树的子树有左右之分。

(4)二叉树的性质

性质1：二叉树中层数为的结点至多有个。

性质2：高度为的二叉树至多有个结点。

若一棵高度为的二叉树，具有个结点，这样的二叉树称为满二叉树。

若一棵具有个结点，高度为的二叉树，其中所有结点与高度为的满二叉树中编号由1至的那些结点对应，这样的二叉树称为完全二叉树。

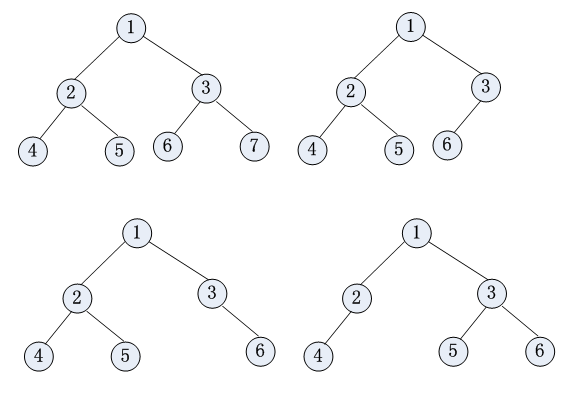
注：满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

性质3：设二叉树中叶子结点的个数为，度为2结点的个数为，则。

性质4：将一棵具有个结点的完全二叉树按层次顺序(从上到下、从左到右)从1开始编号，则对编号为的结点有：

• 若不等于1，则编号为结点的双亲结点的编号为；
• 若，则编号为结点的左孩子的编号为，否则无左孩子；
• 若，则编号为结点的右孩子的编号为，否则无右孩子；

性质5：具有个结点的完全二叉树的高度为。

2.2 二叉树的存储

(1)顺序存储

完全二叉树：

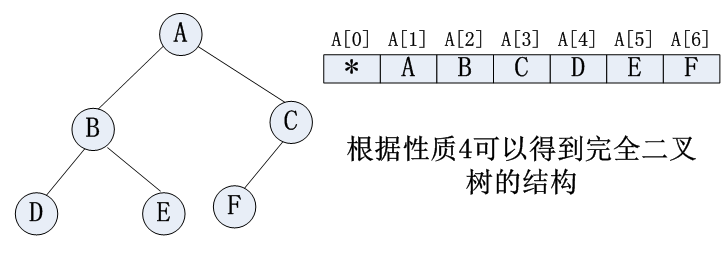
非完全二叉树：

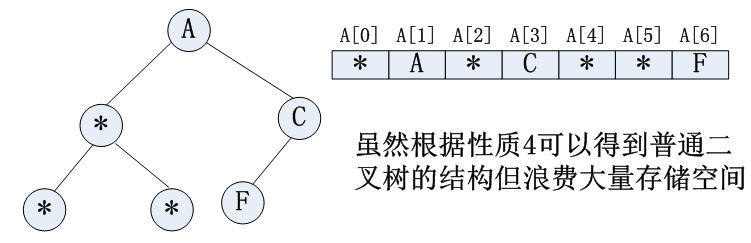
(2)链式存储

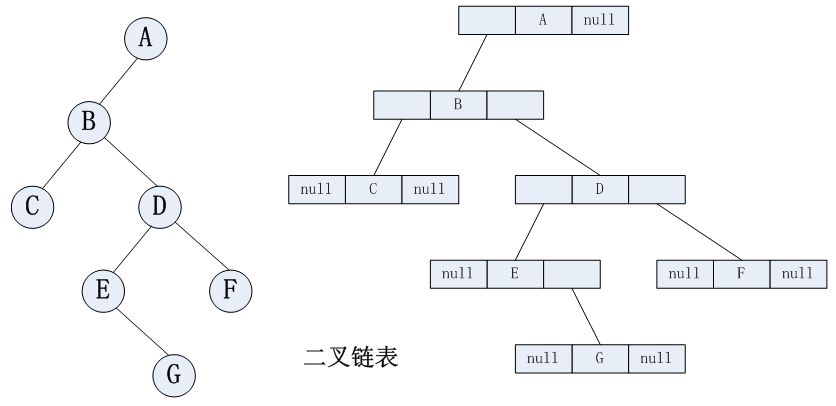
通常：完全二叉树用顺序存储，普通二叉树用链式存储。

二叉树结点的结构：

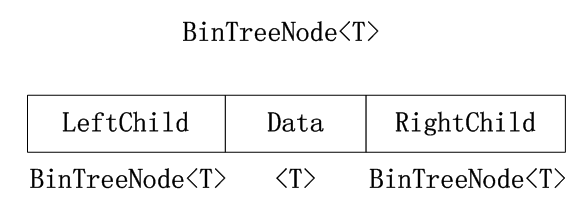
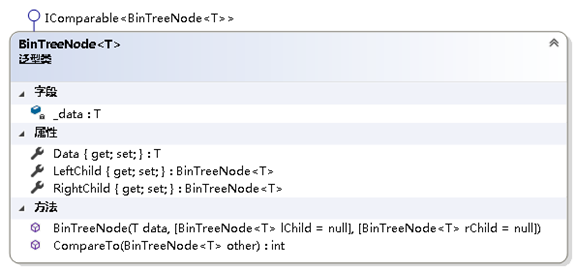
using System;namespace NonLinearStruct{    ///     /// 二叉树结点    ///     /// 结点中数据元素的类型    public class BinTreeNode : IComparable> where T : IComparable    {private T _data;/// /// 获取或设置该结点的左孩子/// public BinTreeNode LeftChild { get; set; }/// /// 获取或设置该结点的右孩子/// public BinTreeNode RightChild { get; set; }/// /// 获取或设置该结点的数据元素/// public T Data        {            get { return _data; }set            {if (value == null)throw new ArgumentNullException();                _data = value;            }        }/// /// 初始化BinTreeNode类的新实例/// /// 该结点的左孩子///    该结点的数据元素 /// 该结点的右孩子public BinTreeNode(T data, BinTreeNode lChild = null, BinTreeNode rChild = null){if (data == null)throw new ArgumentNullException();            LeftChild = lChild;            _data = data;            RightChild = rChild;        }/// /// 实现接口IComparable>中的方法。/// /// /// public int CompareTo(BinTreeNode other){if (other == null)throw new ArgumentNullException();return _data.CompareTo(other.Data);        }    }}

2.3 二叉树的遍历

定义：按照一定次序访问树中所有结点，并且每个结点的值仅被访问一次的过程。

遍历的方式：

• 前序遍历(先根遍历)：访问根结点，前序遍历左子树，前序遍历右子树；
• 中序遍历(中根遍历)：中序遍历左子树，访问根结点，中序遍历右子树；
• 后序遍历(后根遍历)：后序遍历左子树，后序遍历右子树，访问根结点
• 层次遍历：遍历第0层，遍历第1层，，遍历第层(为树的深度)；

例子：

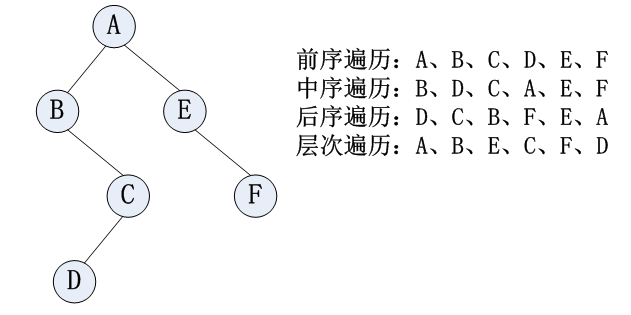
例子：中序遍历与递归

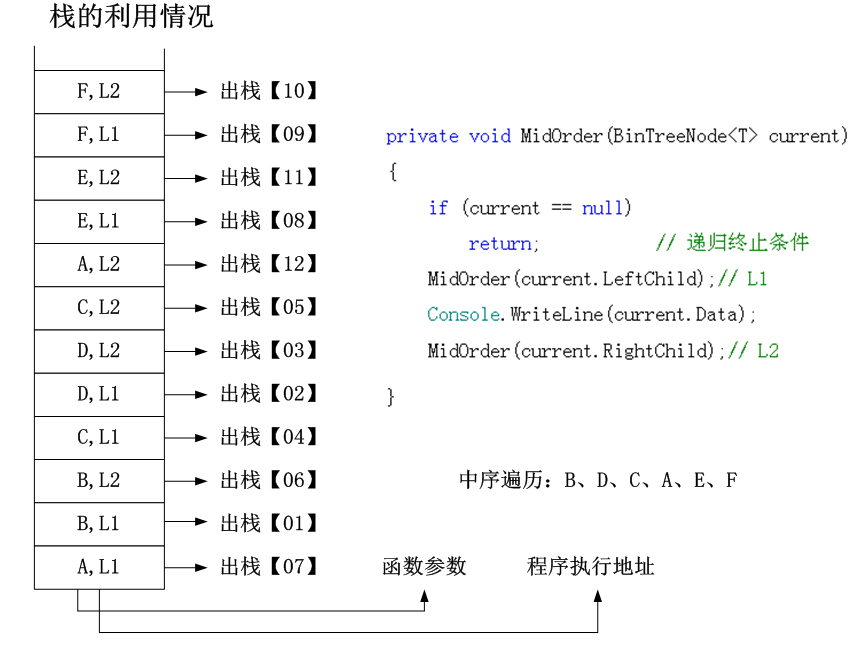
2.4 二叉树的实现

二叉树的操作

• 获取或设置二叉树的根结点
• 向二叉树中插入结点
• 获取前序遍历序列
• 获取中序遍历序列
• 获取后序遍历序列
• 获取层次遍历序列
• 获取给定结点的双亲结点
• 获取给定结点的左兄弟结点
• 获取给定结点的右兄弟结点
• 删除以给定结点为根的子树
• 根据给定数据查找其在二叉树中的结点
• 获取叶子结点的个数
• 交换二叉树的左右子树

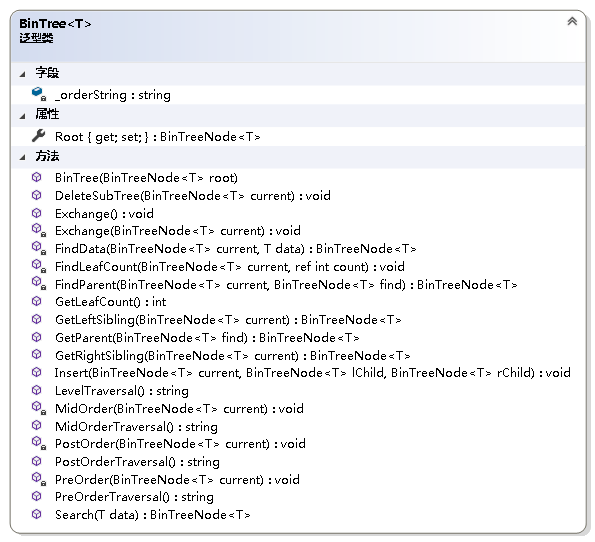
using System;using LinearStruct;namespace NonLinearStruct{    ///     /// 二叉树的抽象数据类型实现    ///     /// 二叉树中结点数据的类型    public class BinTree where T : IComparable    {private string _orderString = string.Empty;/// /// 获取或设置二叉树的根结点/// public BinTreeNode Root { get; set; }/// /// 初始化BinTree类的新实例/// /// 二叉树的根结点public BinTree(BinTreeNode root){            Root = root;        }/// /// 向树中插入结点/// /// 要插入的结点/// 该结点的左孩子结点/// 该结点的右孩子结点public void Insert(BinTreeNode current, BinTreeNode lChild, BinTreeNode rChild){if (Root == null)throw new Exception("树为空.");if (current == null)throw new ArgumentNullException();            current.LeftChild = lChild;            current.RightChild = rChild;        }/// /// 前序遍历的递归函数/// /// 开始递归的根结点private void PreOrder(BinTreeNode current){if (current == null)return;            _orderString += current.Data + " ";            PreOrder(current.LeftChild);            PreOrder(current.RightChild);        }/// /// 得到前序遍历序列/// /// 前序遍历序列public string PreOrderTraversal(){            _orderString = string.Empty;            PreOrder(Root);return _orderString.Trim();        }/// /// 中序遍历的递归函数/// /// 开始递归的根结点private void MidOrder(BinTreeNode current){if (current == null)return;            MidOrder(current.LeftChild);            _orderString += current.Data + " ";            MidOrder(current.RightChild);        }/// /// 得到中序遍历序列/// /// 中序遍历序列public string MidOrderTraversal(){            _orderString = string.Empty;            MidOrder(Root);return _orderString.Trim();        }/// /// 后序遍历的递归函数/// /// 开始递归的根结点private void PostOrder(BinTreeNode current){if (current == null)return;            PostOrder(current.LeftChild);            PostOrder(current.RightChild);            _orderString += current.Data + " ";        }/// /// 得到后序遍历序列/// /// 后序遍历序列public string PostOrderTraversal(){            _orderString = string.Empty;            PostOrder(Root);return _orderString.Trim();        }/// /// 得到层次遍历序列/// /// 层次遍历序列public string LevelTraversal(){            _orderString = string.Empty;if (Root != null)            {                LinkQueue> lq = new LinkQueue>();                lq.EnQueue(Root);while (lq.IsEmpty() == false)                {                    BinTreeNode temp = lq.QueueFront;                    lq.DeQueue();                    _orderString += temp.Data + " ";if (temp.LeftChild != null)                        lq.EnQueue(temp.LeftChild);if (temp.RightChild != null)                        lq.EnQueue(temp.RightChild);                }            }return _orderString.Trim();        }/// /// 从current结点开始寻找find结点的父亲结点的递归函数/// /// 开始递归的根结点/// 要寻找的结点/// find结点的父亲结点private BinTreeNode FindParent(BinTreeNode current, BinTreeNode find){if (find == null)throw new ArgumentNullException();if (current == null)return null;if (current.LeftChild != null && current.LeftChild.Equals(find))return current;if (current.RightChild != null && current.RightChild.Equals(find))return current;            BinTreeNode temp = FindParent(current.LeftChild, find);if (temp != null)return temp;return FindParent(current.RightChild, find);        }/// /// 得到find结点的父亲结点,若不存在返回null./// /// 要寻找的结点/// 该结点的父亲结点public BinTreeNode GetParent(BinTreeNode find){if (find == null)throw new ArgumentNullException();return FindParent(Root, find);        }/// /// 得到当前结点的左兄弟结点,若不存在返回null./// /// 当前结点/// 当前结点的左兄弟结点public BinTreeNode GetLeftSibling(BinTreeNode current){if (current == null)throw new ArgumentNullException();            BinTreeNode parent = GetParent(current);if (parent != null && parent.LeftChild != null && parent.LeftChild.Equals(current) == false)return parent.LeftChild;return null;        }/// /// 得到当前结点的右兄弟结点,若不存在返回null./// /// 当前结点/// 当前结点的右兄弟结点public BinTreeNode GetRightSibling(BinTreeNode current){if (current == null)throw new ArgumentNullException();            BinTreeNode parent = GetParent(current);if (parent != null && parent.RightChild != null && parent.RightChild.Equals(current) == false)return parent.RightChild;return null;        }/// /// 删除以current为根的子树/// /// 要删除子树的根public void DeleteSubTree(BinTreeNode current){if (current == null)throw new ArgumentNullException();if (Root == null)throw new Exception("二叉树为null.");if (Root.Equals(current))            {                Root = null;            }else            {                BinTreeNode parent = GetParent(current);if (parent != null && parent.LeftChild != null && parent.LeftChild.Equals(current))                    parent.LeftChild = null;if (parent != null && parent.RightChild != null && parent.RightChild.Equals(current))                    parent.RightChild = null;            }        }/// /// 寻找结点的递归函数/// /// 开始结点/// 数据/// 数据所在的结点private BinTreeNode FindData(BinTreeNode current, T data){if (data == null)throw new ArgumentNullException();if (current == null)return null;if (current.Data.CompareTo(data) == 0)return current;            BinTreeNode temp = FindData(current.LeftChild, data);if (temp != null)return temp;return FindData(current.RightChild, data);        }/// /// 根据数据的值找到二叉树中对应的结点,若不存在返回null./// /// 数据的值/// 二叉树中对应的结点public BinTreeNode Search(T data){if (data == null)throw new ArgumentNullException();return FindData(Root, data);        }/// /// 统计叶子结点个数的递归函数/// /// 统计叶子结点子树的根/// 叶子结点的个数private void FindLeafCount(BinTreeNode current, ref int count){if (current == null)return;if (current.LeftChild == null && current.RightChild == null)            {                count++;return;            }            FindLeafCount(current.LeftChild, ref count);            FindLeafCount(current.RightChild, ref count);        }/// /// 得到该树叶子结点的个数/// /// 叶子结点的个数public int GetLeafCount(){int count = 0;            FindLeafCount(Root, ref count);return count;        }/// /// 交换左右子树的递归函数/// /// 子树的根结点private void Exchange(BinTreeNode current){if (current == null)return;if (current.LeftChild != null || current.RightChild != null)            {                BinTreeNode temp = current.LeftChild;                current.LeftChild = current.RightChild;                current.RightChild = temp;            }if (current.LeftChild != null)                Exchange(current.LeftChild);if (current.RightChild != null)                Exchange(current.RightChild);        }/// /// 交换二叉树的左右子树/// public void Exchange(){            Exchange(Root);        }    }}

例子：

class Program{    static void Main(string[] args){        BinTreeNode<string> a = new BinTreeNode<string>("A");        BinTreeNode<string> b = new BinTreeNode<string>("B");        BinTreeNode<string> c = new BinTreeNode<string>("C");        BinTreeNode<string> d = new BinTreeNode<string>("D");        BinTree<string> bintree = new BinTree<string>(a);        bintree.Insert(a, b, c);        bintree.Insert(b, d, null);        Console.WriteLine("前序遍历:{0}", bintree.PreOrderTraversal());        // 前序遍历:A B D C        Console.WriteLine("中序遍历:{0}", bintree.MidOrderTraversal());        // 中序遍历:D B A C        Console.WriteLine("后序遍历:{0}", bintree.PostOrderTraversal());        // 后序遍历:D B C A        Console.WriteLine("层次遍历:{0}", bintree.LevelTraversal());        // 层次遍历:A B C D        BinTreeNode<string> parent = bintree.GetParent(d);        BinTreeNode<string> lSibling = bintree.GetLeftSibling(c);        BinTreeNode<string> rSibling = bintree.GetRightSibling(b);        if (parent != null)            Console.WriteLine("结点{0}的Parent结点:{1}", d.Data, parent.Data);        else            Console.WriteLine("结点{0}无Parent.", d.Data);        // 结点D的Parent结点:B        if (lSibling != null)            Console.WriteLine("结点{0}的左兄弟结点:{1}", c.Data, lSibling.Data);        else            Console.WriteLine("结点{0}无左兄弟结点.", c.Data);        // 结点C的左兄弟结点:B                if (lSibling != null)            Console.WriteLine("结点{0}的右兄弟结点:{1}", b.Data, rSibling.Data);        else            Console.WriteLine("结点{0}无右兄弟结点.", b.Data);        // 结点B的右兄弟结点:C        bintree.DeleteSubTree(d);        Console.WriteLine("把结点{0}从二叉树中移除.", d.Data);        // 把结点D从二叉树中移除.        Console.WriteLine("前序遍历:{0}", bintree.PreOrderTraversal());        // 前序遍历: A B C        Console.WriteLine("中序遍历:{0}", bintree.MidOrderTraversal());        // 中序遍历:B A C                    Console.WriteLine("后序遍历:{0}", bintree.PostOrderTraversal());        // 后序遍历: B C A                    Console.WriteLine("层次遍历:{0}", bintree.LevelTraversal());        // 层次遍历: A B C        BinTreeNode<string> e = bintree.Search("A");        if (e != null && e.LeftChild != null)            Console.WriteLine("寻找结点{0}的左孩子为{1}", e.Data, e.LeftChild.Data);        else            Console.WriteLine("未找到{0}结点或者{0}结点左孩子为null", a.Data);        // 寻找结点A的左孩子为B                Console.WriteLine("叶子结点的个数:{0}", bintree.GetLeafCount());        // 叶子结点的个数:2        bintree.Exchange();        Console.WriteLine("前序遍历:{0}", bintree.PreOrderTraversal());        // 前序遍历:A C B        Console.WriteLine("中序遍历:{0}", bintree.MidOrderTraversal());        // 中序遍历: C A B                    Console.WriteLine("后序遍历:{0}", bintree.PostOrderTraversal());        // 后序遍历: C B A                    Console.WriteLine("层次遍历:{0}", bintree.LevelTraversal());        // 层次遍历: A C B    }}

---

3. 树与森林

3.1 树的存储

(1)顺序存储

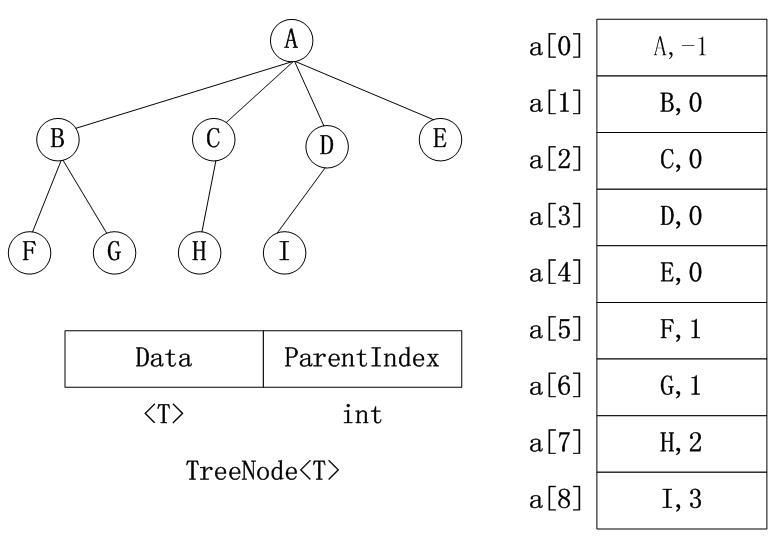
(2)链式存储

A. 存储双亲结点

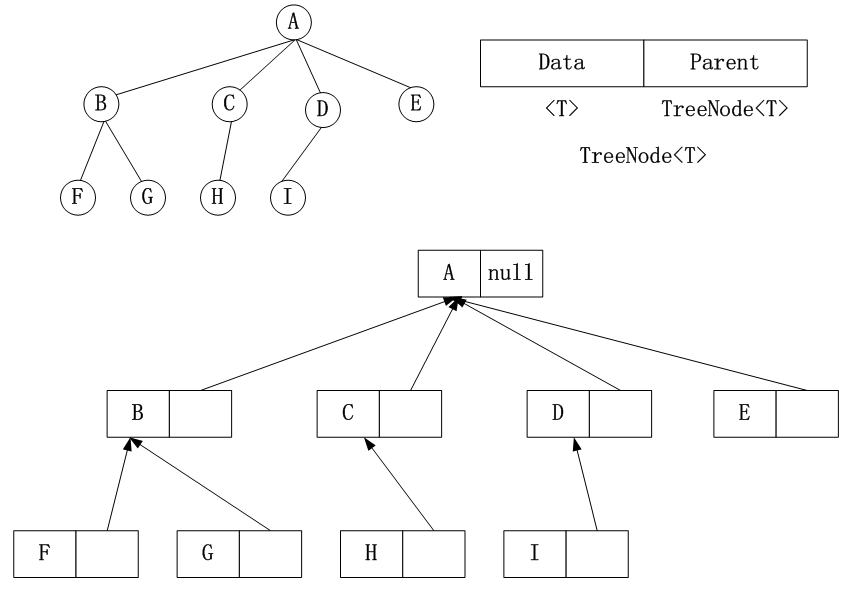
B. 存储孩子结点

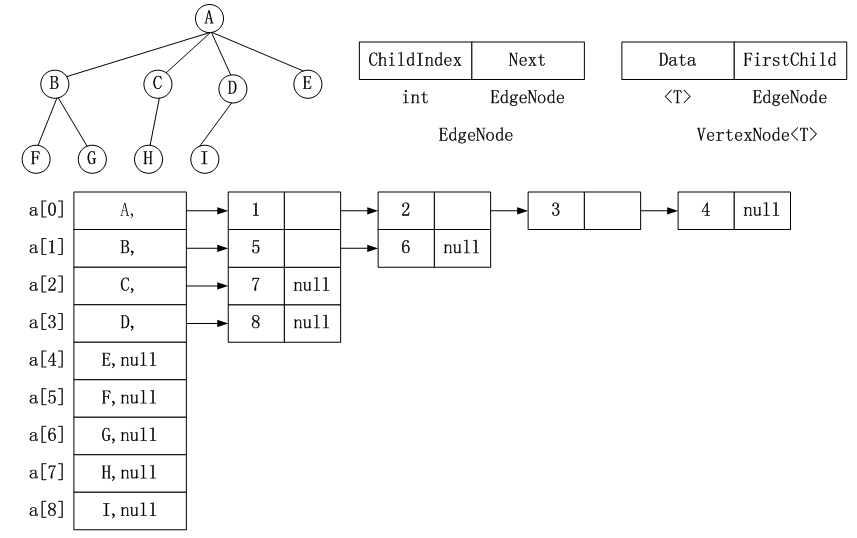
C. 存储孩子和兄弟结点

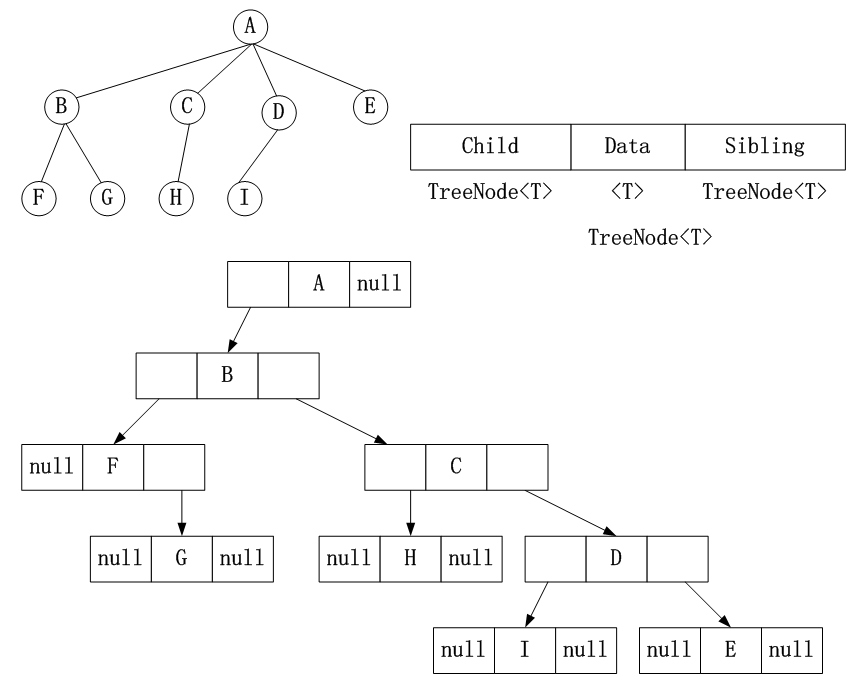
3.2 树与二叉树的相互转换

(1)树转换成二叉树

按照左孩子，右兄弟规则。

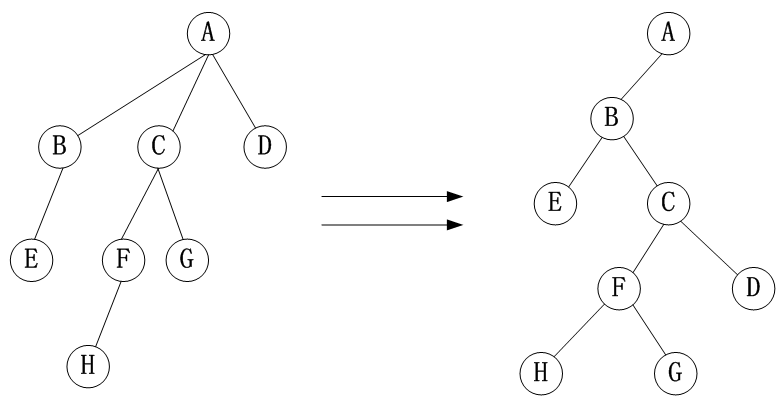
(2)二叉树转换成树

按照左孩子，右兄弟规则的逆过程。

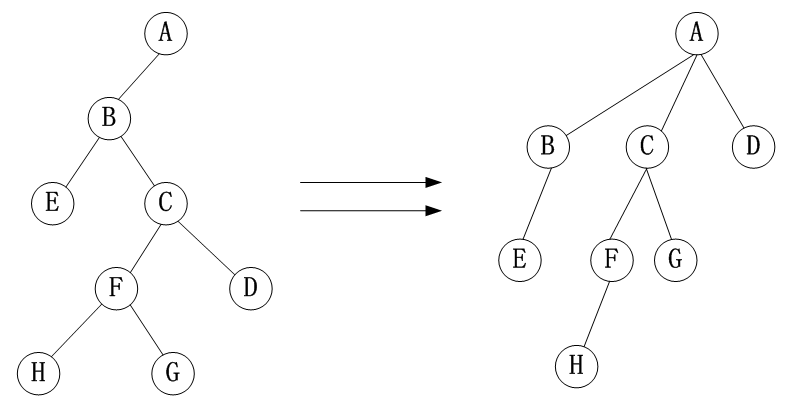
3.3 森林与二叉树的相互转换

(1)森林转化成二叉树

设为树组成的森林，为其对应的二叉树。

• 若，则。
• 若，`的根为，的左子树由的诸子树组成，右子树由组成。

方式1：

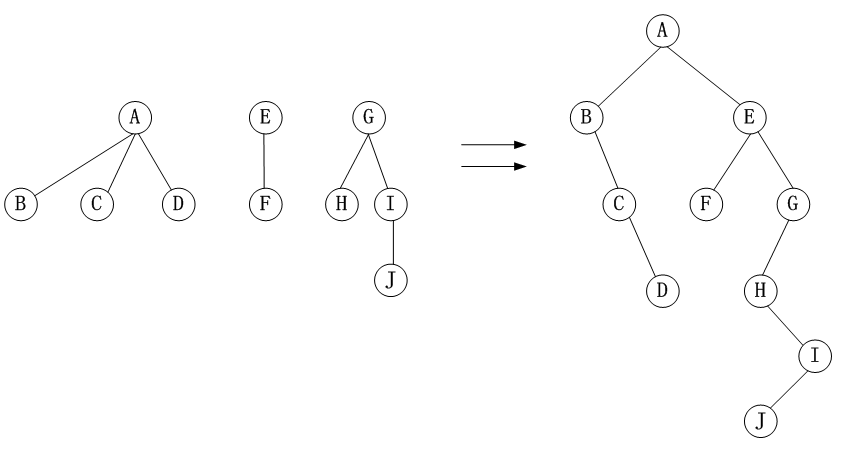
方式2：

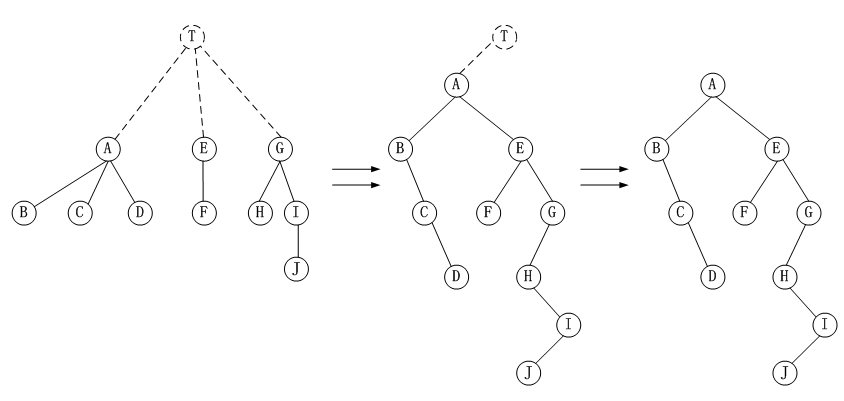
(2)二叉树转化成森林

设是一颗二叉树，为其对应的森林。

• 若，则 。
• 若不等于，则的根为二叉树的根，的子树森林由的左子树转换而成，其余树组成的森林由的右子树转换而成。

方式1：

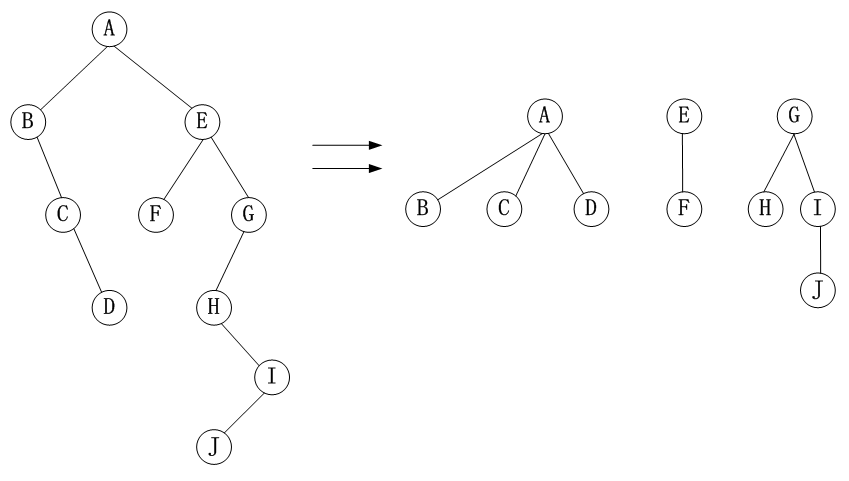
方式2：

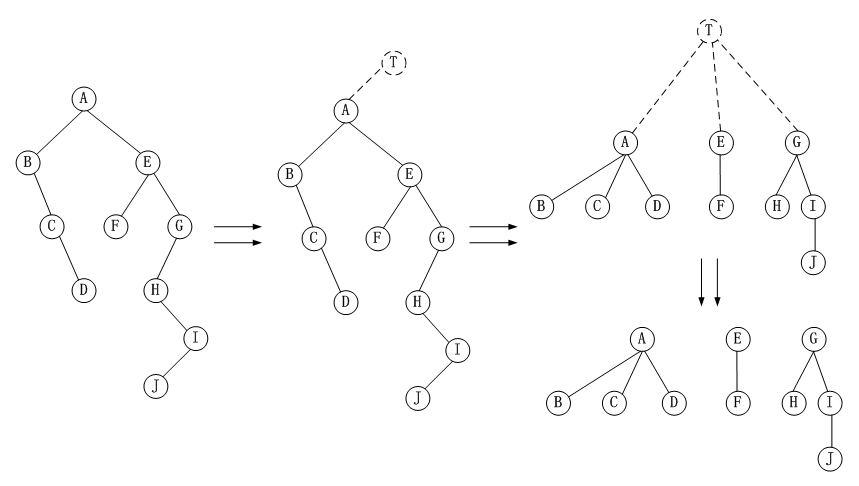
3.4 树与森林的遍历

(1)树的遍历

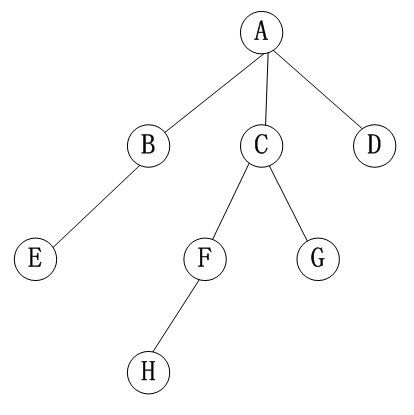
前序遍历：首先访问根结点；然后前序遍历每棵子树。

• 前序遍历序列：A B E C F H G D

后序遍历：首先后序遍历每棵子树；然后访问根结点。

• 后序遍历序列：E B H F G C D A

(2)森林的遍历

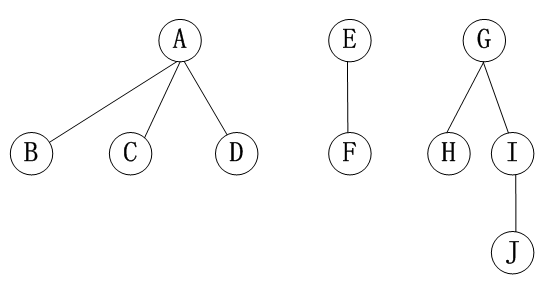
前序遍历：首先访问第一棵树的根结点；然后前序遍历第一棵树的子树；再前序遍历由其余树组成的森林。

• 前序遍历序列：A B C D E F G H I J

后序遍历：先后序遍历第一棵树的子树；然后访问第一棵树的根结点；再后序遍历由其余树组成的森林。

• 后序遍历序列：B C D A F E H J I G

---

4. 线索二叉树

4.1 引入

性质：设二叉树利用二叉链表存储且结点个数为，则该二叉树的链域个数为，空链域个数为。

想法：利用空链域存储该树按照某种方式遍历(前序、中序、后序)的前趋或后继结点。

结构：

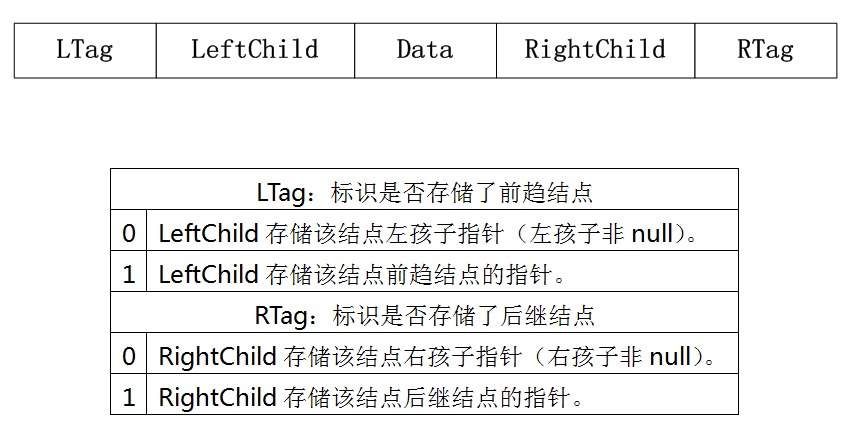
4.2 相关概念

线索：在这种结构中指向其前趋或后继结点的指针。

线索二叉树：加上线索的二叉树。

线索化：把二叉树变成线索二叉树的过程。

线索化的方式：前序线索化、中序线索化、后序线索化

例子：中序线索化

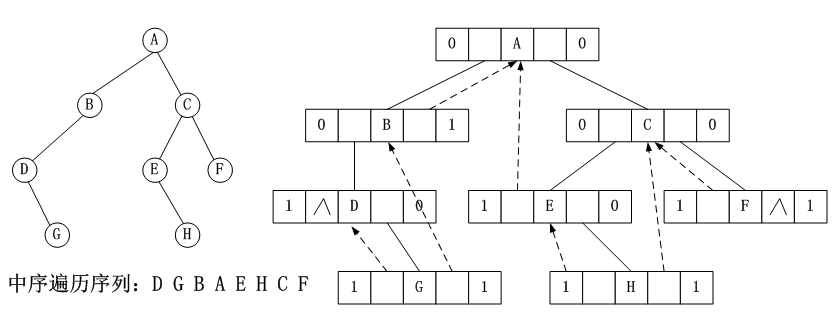
例子：前序线索化

---

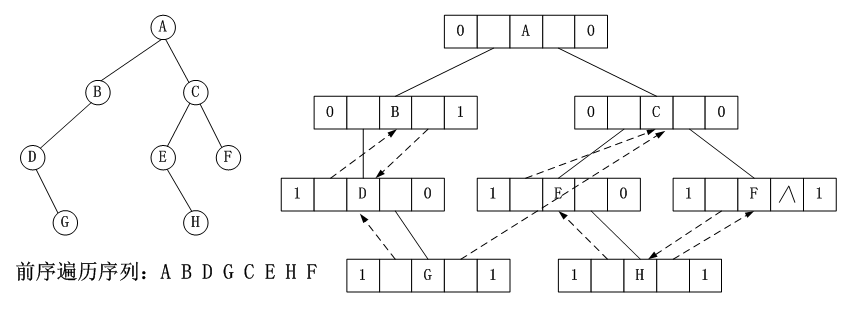
5. 哈夫曼树及其编码(Huffman)

5.1 哈夫曼树的定义

路径：连接两个结点的分支，构成这两个结点的路径。

路径长度：两个结点路径上的分支数。

结点的权：为结点赋的一个有意义的实数。

结点的带权路径长度：根结点到该结点的路径长度与该结点权值的乘积。

树的带权路径长度：树中所有叶子结点的带权路径长度之和。记为：，为叶子结点的个数。

哈夫曼树：个带权叶子结点构成的所有二叉树中，带权路径长度最小的二叉树。(最优二叉树)

5.2 哈夫曼树的构造

第1步：根据给定的个权值，构成棵二叉树的森林，其中每棵二叉树中都只有一个权值`的根结点，其左右子树均为空。

第2步：在森林中选出两棵根结点权值最小的树作为一棵新树的左右子树，且置新树的根结点的权值为其左右子树上根结点的权值之和。

第3步：从中删除构成新树的哪两棵树，同时把新树加入中。

第4步：重复第2和3步，直到中只含有一棵树为止，此树便是Huffman树。

例子：给定权集 ，试构造关于的一颗哈夫曼树，并求其带权路径长度 。

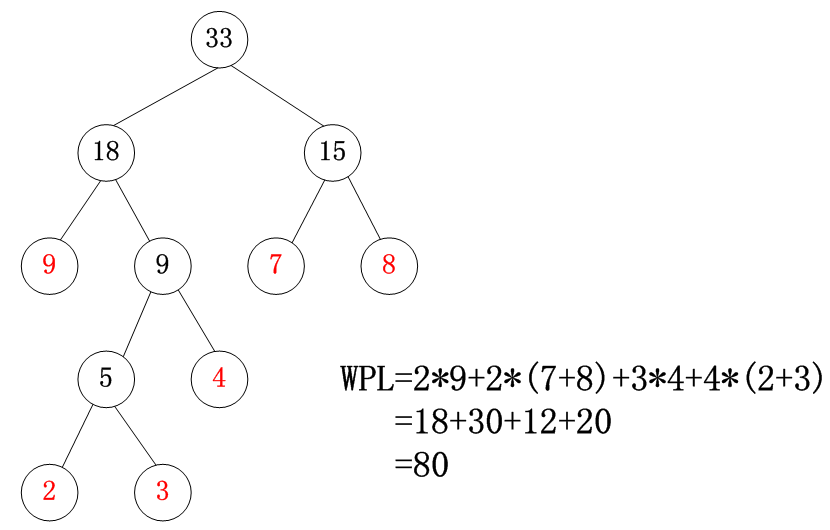
5.3 哈夫曼编码的概念

前缀码规则：对字符集编码时，字符集中任一字符的编码都不是其它字符编码的前缀。

例子：

A：0 B：00 C：01 D：10(违反前缀码规则)

000010  BBD、AAAAD、BAAD、AABD (不唯一，解码时有二义性)

A：00 B：01 C：10 D：11(满足前缀码规则)

000010  AAC (唯一)

哈夫曼编码：将哈夫曼树中，每个分支结点的左分支标0，右分支标1，把从根结点到每个叶子结点的路径上的标号连接起来作为该叶子结点所代表符号的编码，这样得到的编码称为Huffman编码。(优点：满足前缀码规则)

例子：对所要发送的数据进行二进制编码。

state，seat，act，tea，cat，set，a，eat

第一种编码方式：

's'："000” 't'：“001” 'a'：“010” 'e'：“011” 'c'：“100” ','：“110”

此种编码满足前缀码规则，但编码过长。eat：011010001

第二种编码方式：

统计字符出现的频数：‘s’：3  ‘t’：8  ‘a’：7  ‘e’：5  ‘c’：2 ‘,’：7

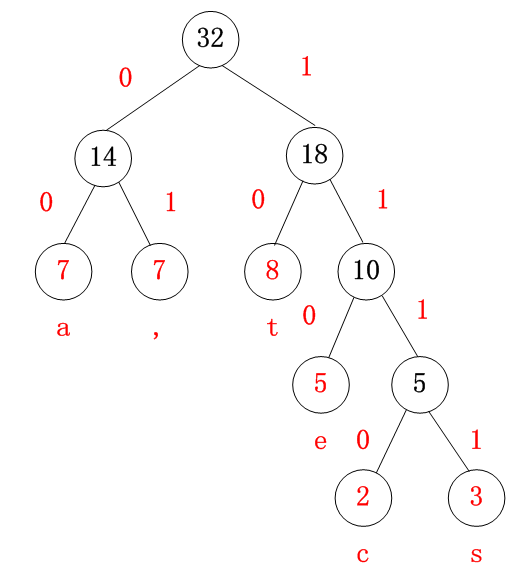
'a'："00” ','：“01” 't'：“10” 'e'：“110” 'c'：“1110” 's'：“1111”

• eat：1100010
• state：1111100010110
• seat：11111100010

5.4 哈夫曼编码的实现

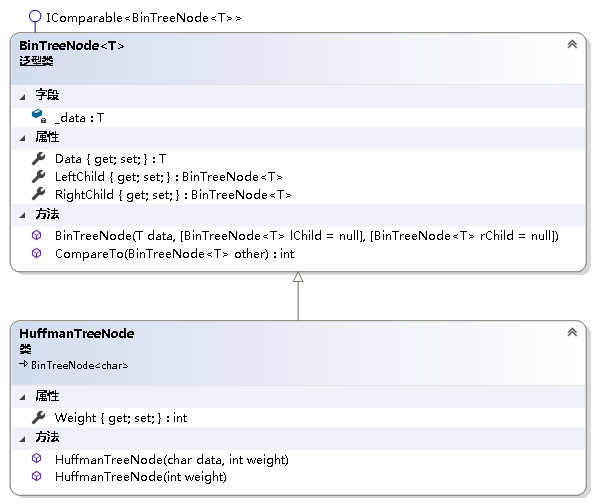
namespace NonLinearStruct{    ///     /// 表示Huffman树的结点    ///     public class HuffmanTreeNode : BinTreeNode<char>    {        ///         /// 结点的权值        ///         public int Weight { get; set; }        ///         /// 叶子结点 -- 字符        ///         /// 字符        /// 结点的权        public HuffmanTreeNode(char data, int weight) : base(data){            Weight = weight;        }        ///         /// 其它结点        ///         /// 结点的权        public HuffmanTreeNode(int weight) : base('\0'){            Weight = weight;        }    }}

namespace NonLinearStruct{    ///     /// Huffman字典    ///     public class HuffmanDicItem    {        ///         /// 获取或设置字符        ///         public char Character { get; set; }        ///         /// 获取或设置编码        ///         public string Code { get; set; }        ///         /// 构造函数        ///         /// 字符        /// 编码        public HuffmanDicItem(char charactor, string code){            Character = charactor;            Code = code;        }    }}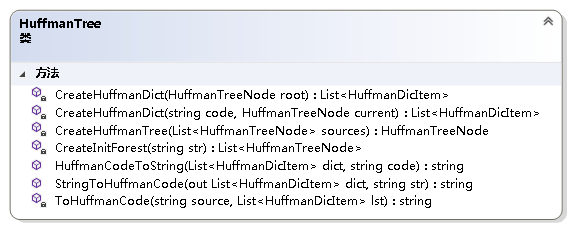

using System;using System.Collections.Generic;using System.Linq;namespace NonLinearStruct{    ///     /// Huffman树    ///     public class HuffmanTree    {        ///         /// 构造Huffman树初始的森林        ///         /// 字符串        /// 结点的集合，构成初始的森林        private List CreateInitForest(string str){            if (string.IsNullOrEmpty(str))                throw new ArgumentNullException();            List result = new List();char[] charArray = str.ToCharArray();            Listchar, char>> lst = charArray.GroupBy(a => a).ToList();            foreach (IGrouping<char, char> g in lst)            {char data = g.Key;int weight = g.ToList().Count;                HuffmanTreeNode node = new HuffmanTreeNode(data, weight);                result.Add(node);            }return result;        }/// /// 构造Huffman树/// /// 初始的结点的集合/// Huffman树的Rootprivate HuffmanTreeNode CreateHuffmanTree(List sources){if (sources == null)throw new ArgumentNullException();if (sources.Count 2)throw new ArgumentException("构造Huffman树，最少为2个结点。");            HuffmanTreeNode root = default(HuffmanTreeNode);bool isNext = true;while (isNext)            {                List lst = sources.OrderBy(a => a.Weight).ToList();                HuffmanTreeNode n1 = lst[0];                HuffmanTreeNode n2 = lst[1];int weight = n1.Weight + n2.Weight;                HuffmanTreeNode node = new HuffmanTreeNode(weight);                node.LeftChild = n1;                node.RightChild = n2;if (lst.Count == 2)                {                    root = node;                    isNext = false;                }else                {                    sources = lst.GetRange(2, lst.Count - 2);                    sources.Add(node);                }            }return root;        }/// /// 创建Huffman编码的字典/// /// /// /// private List CreateHuffmanDict(string code, HuffmanTreeNode current){if (current == null)throw new ArgumentNullException();            List result = new List();if (current.LeftChild == null && current.RightChild == null)            {                result.Add(new HuffmanDicItem(current.Data, code));            }else            {                List dictL = CreateHuffmanDict(code + "0",                    (HuffmanTreeNode)current.LeftChild);                List dictR = CreateHuffmanDict(code + "1",                    (HuffmanTreeNode)current.RightChild);                result.AddRange(dictL);                result.AddRange(dictR);            }return result;        }/// /// 创建Huffman编码的字典/// /// Huffman树/// Huffman字典private List CreateHuffmanDict(HuffmanTreeNode root){if (root == null)throw new ArgumentNullException();return CreateHuffmanDict(string.Empty, root);        }/// /// 对字符串进行编码/// /// Huffman字典/// 编码字符串/// 编码后的字符串public string StringToHuffmanCode(out List dict, string str){            List forest = CreateInitForest(str);            HuffmanTreeNode root = CreateHuffmanTree(forest);            dict = CreateHuffmanDict(root);string result = ToHuffmanCode(str, dict);return result;        }/// /// 给定Huffman字典对编码进行解码/// /// Huffman字典/// 解码的字符/// 解码后的字符public string HuffmanCodeToString(List dict, string code){string result = string.Empty;for (int i = 0; i             {                foreach (HuffmanDicItem item in dict)                {if (code[i] == item.Code[0] && item.Code.Length + i <= code.Length)                    {string temp = code.Substring(i, item.Code.Length);if (temp == item.Code)                        {                            result += item.Character;                            i += item.Code.Length;break;                        }                    }                }            }return result;        }/// /// 利用Huffman字典对字符集进行编码/// /// 编码的字符/// Huffman字典/// 编码后的字符串private string ToHuffmanCode(string source, List lst){if (string.IsNullOrEmpty(source))throw new ArgumentNullException();if (lst == null)throw new ArgumentNullException();string result = string.Empty;for (int i = 0; i             {                result += lst.Single(a => a.Character == source[i]).Code;            }return result;        }    }}

客户端代码：

class Program{    static void Main(string[] args){        string str = "state,seat,act,tea,cat,set,a,eat";        Console.WriteLine(str);        // state,seat,act,tea,cat,set,a,eat        HuffmanTree huffmanTree = new HuffmanTree();        List dic;string huffmanCode = huffmanTree.StringToHuffmanCode(out dic, str);string temp = string.Empty;for (int i = 0; i         {            temp += @"'" + dic[i].Character + "':" + "\"" + dic[i].Code + "\"\r\n";        }        Console.WriteLine(temp.Substring(0, temp.Length - 2));//  'a':"00"//  ',':"01"//  't':"10"//  'e':"110"//  'c':"1110"//  's':"1111"        Console.WriteLine(huffmanCode);// 1111100010110011111110001001001110100110110000111100010011111110100100011100010string decode = huffmanTree.HuffmanCodeToString(dic, huffmanCode);        Console.WriteLine(decode);//state,seat,act,tea,cat,set,a,eat    }}

---