小波时频图

 一、绘制原理：

1.需要用到的小波工具箱中的三个函数cwt()，centfrq()，scal2frq()

COEFS = cwt(S,SCALES,'wname')

该函数实现连续小波变换，其中S为输入信号，SCALES为尺度，wname为小波名称。

 

FREQ = centfrq('wname')

该函数求以wname命名的母小波的中心频率。

 

F = scal2frq(A,'wname',DELTA)

该函数能将尺度转换为实际频率，其中A为尺度，wname为小波名称，DELTA为采样周期。

 

2.尺度与频率之间的关系

设a为尺度，fs为采样频率，Fc为小波中心频率，则a对应的实际频率Fa为

Fa＝Fc*fs/a

显然，根据采样定理，为使小波尺度图的频率范围为(0,fs/2)，尺度范围应为(2*Fc,inf),其中inf表示为无穷大。在实际应用中，只需取尺度足够大即可。

 

3.尺度序列的确定

由上式可以看出，为使转换后的频率序列是一等差序列，尺度序列必须取为以下形式：

c/totalscal, c/(totalscal-1), ...,c/2,c

其中，totalscal是对信号进行小波变换时所用尺度序列的长度(通常需要预先设定好)，c为一常数。

而尺度c/totalscal所对应的实际频率应为fs/2，于是可得

c=2*Fc*totalscal

于是可得到所需的尺度序列。

 

4.时频图的绘制

确定了小波基和尺度后，就可以用cwt求小波系数coefs（系数是复数时要取模），然后用scal2frq将尺度序列转换为实际频率序列f，最后结合时间序列t，用imagesc(t,f,abs(coefs))便能画出小波时频图。

 

二、应用例子

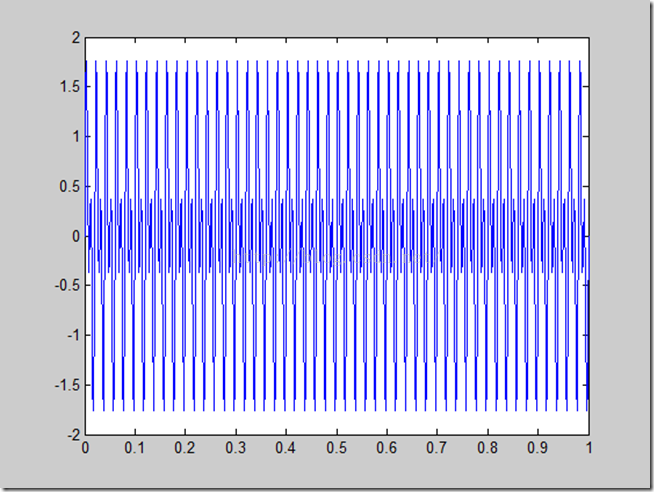
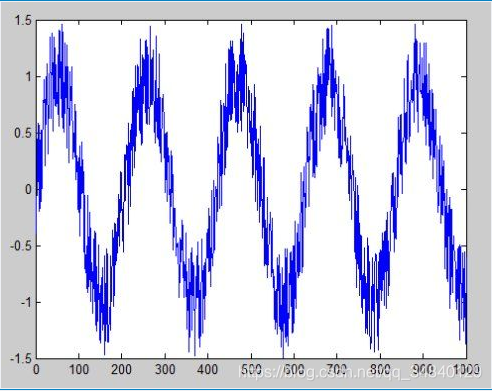
下面给出一实际例子来说明小波时频图的绘制。所取仿真信号是由频率分别为50Hz和100Hz的两个正弦分量所合成的信号。

% 小波时频分析
 
clc
 
clear all
 
close all
 
% 原始信号
 
fs=1000;
 
f1=50;
 
f2=100;
 
t=0:1/fs:1;
 
s=sin(2*pi*f1*t)+sin(2*pi*f2*t);
 
figure
 
plot(t, s)
 
% 连续小波变换
 
wavename='cmor3-3';
 
totalscal=256;
 
Fc=centfrq(wavename); % 小波的中心频率
 
c=2*Fc*totalscal;
 
scals=c./(1:totalscal);
 
f=scal2frq(scals,wavename,1/fs); % 将尺度转换为频率
 
coefs=cwt(s,scals,wavename); % 求连续小波系数
 
figure
 
imagesc(t,f,abs(coefs));
 
set(gca,'YDir','normal')
 
colorbar;
 
xlabel('时间 t/s');
 
ylabel('频率 f/Hz');
 
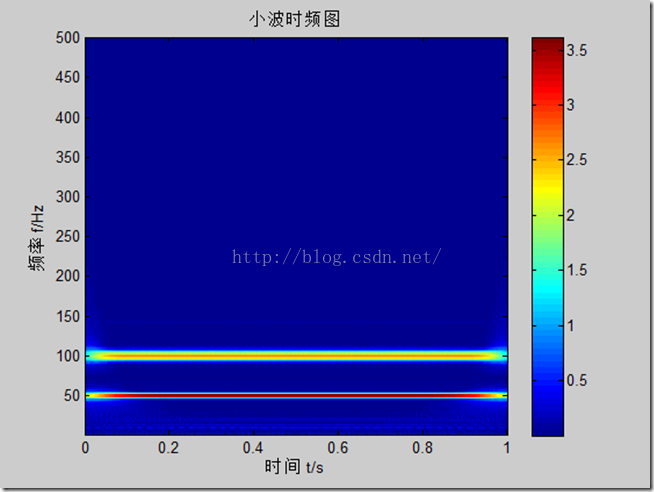
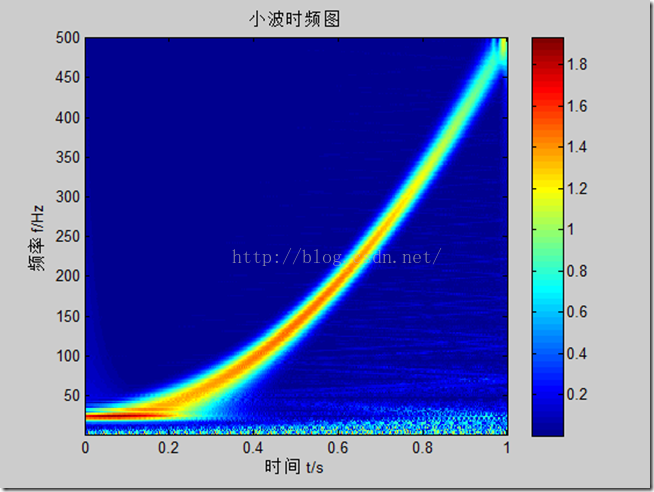
title('小波时频图');

说明：

在这个例子中，最好选用复的morlet小波，其它小波的分析效果不好，而且morlet小波的带宽参数和中心频率取得越大，时频图上反映的时频聚集性越好。

 

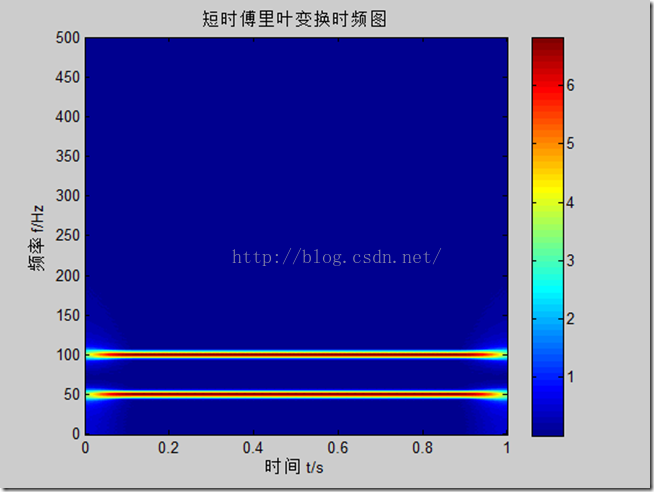
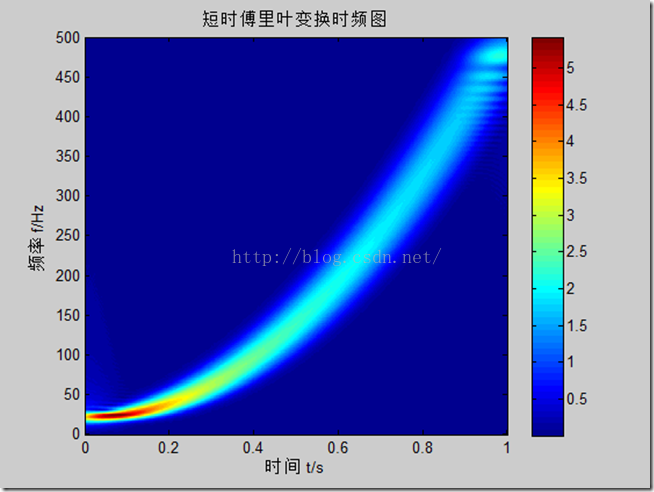
与其他时频分析对比，如短时傅里叶变换时频图

 

小结：

高频时小波效果好，因为小波在高频处分辨率可以自动调整，分辨率高。

代码：

% 时频分析
 
clc
 
clear all
 
close all
 
% 原始信号
 
fs=1000;
 
f1=50;
 
f2=100;
 
t=0:1/fs:1;
 
s = sin(2*pi*f1*t)+sin(2*pi*f2*t);%+randn(1, length(t));
 
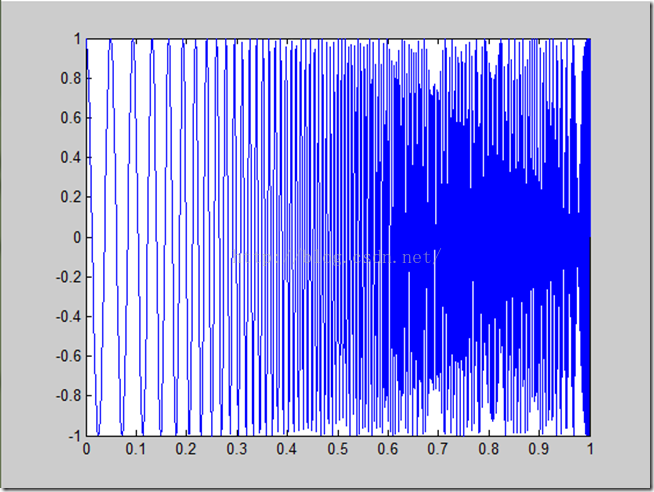
% s = chirp(t,20,0.3,300);
 
s = chirp(t,20,1,500,'q');
 
figure
 
plot(t, s)
 
% 连续小波变换时频图
 
wavename='cmor3-3';
 
totalscal=256;
 
Fc=centfrq(wavename); % 小波的中心频率
 
c=2*Fc*totalscal;
 
scals=c./(1:totalscal);
 
f=scal2frq(scals,wavename,1/fs); % 将尺度转换为频率
 
coefs=cwt(s,scals,wavename); % 求连续小波系数
 
figure
 
imagesc(t,f,abs(coefs));
 
set(gca,'YDir','normal')
 
colorbar;
 
xlabel('时间 t/s');
 
ylabel('频率 f/Hz');
 
title('小波时频图');
 
% 短时傅里叶变换时频图
 
figure
 
spectrogram(s,256,250,256,fs);
 
% 时频分析工具箱里的短时傅里叶变换
 
f = 0:fs/2;
 
tfr = tfrstft(s');
tfr = tfr(1:floor(length(s)/2), :);
figure
imagesc(t, f, abs(tfr));
set(gca,'YDir','normal')
colorbar;
xlabel('时间 t/s');
ylabel('频率 f/Hz');
title('短时傅里叶变换时频图');

 

使用命令行执行连续小波分析

这个例子是一个包含噪声的正弦波

1. 加载信号

load noissin

可以使用whos显示信号信息

whos

Name	Size	Bytes	Class
noissin	1x1000	8000	double

2. 执行连续小波变换

c = cwt(noissin,1:48,'db4');

函数cwt的参数分别为分析的信号、分析的尺度和使用的小波。返回值c包含了在各尺度下的小波系数。对于这里，c是一个48x1000的矩阵，每一行与一个尺度相关。

3. 绘制小波系数

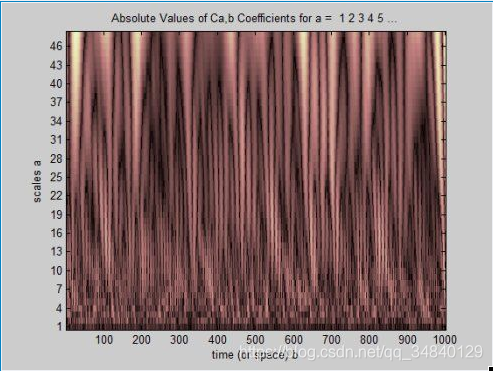
cwt函数可以接受第四个参数，来指定函数在执行结束后是否绘制连续小波变换系数的绝对值。另外还可以接受更多的参数来定义显示的不同特性，详见cwt函数。如下面的语句绘制系数结果

c = cwt(noissin,1:48,'db4','plot');

4. 选择分析的尺度

cwt函数的第二个参数可以设定任意小波分析的尺度，只要这些尺度满足如下要求

l 所有尺幅必须为正实数

l 尺度的增量必须为正

l 最高的尺度不能超过由信号决定的一个最大值

如下面的代码可以执行从2开始的偶数尺度计算

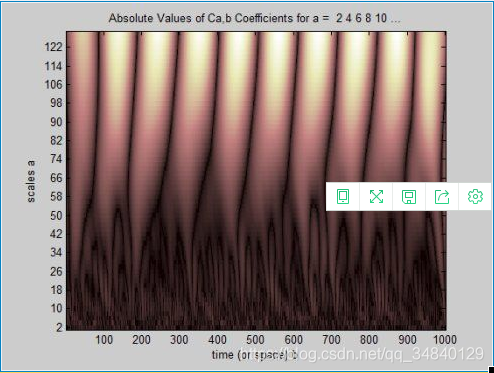
c = cwt(noissin,2:2:128,'db4','plot');

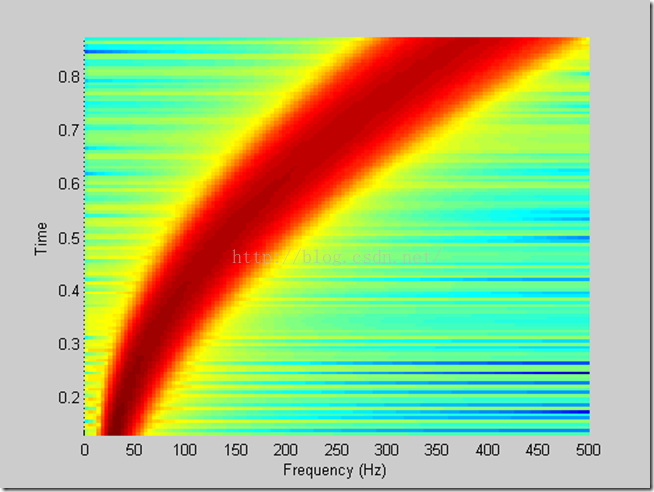
显示结果如下

这幅图像很明确的表示出了信号的周期性。