数据不平衡的常用处理方法_数据不平衡常用解决办法
赞
踩
数据不平衡处理
常见处理方法
1. 欠采样(下采样、Under-sampling、US)
减少分类中多数类样本的样本数量实现样本均衡。
-
随机删除
随机删除一些多量样本。
-
PG算法(Prototype Generation)
在原有样本的基础上生成新的样本来实现样本均衡。

2. 过采样(上采样、over-sampling )
增加分类中少数样本的数量来现样本均衡。
-
随机复制
简单复制少数类样本形成多条记录。缺点:可能导致过拟合问题。
-
样本构建
SMOTE(Synthetic minority over-sampling technique):通过从少量样本集合中筛选的样本 x i x_i xi 和 x j x_j xj及对应的随机数 0 < λ < 1 0<\lambda<1 0<λ<1,通过两个样本间的关系来构建新的样本 x n = x i + λ ( x j − x i ) x_n = x_i + \lambda(x_j -x_i) xn=xi+λ(xj−xi)。
缺点:1)未考率样本分布情况:随机选择样本点组合和 λ \lambda λ参数设置;2)若样本维度过高,样本在空间上的分布会稀疏,由此可能使构建的样本无法代表少量样本的特征。
-
改进算法1——SMOTEBoost:把SMOTE算法和Boost算法结合,在每一轮分类学习过程中增加对少数类的样本的权重,使得基学习器 (base learner) 能够更好地关注到少数类样本。
-
改进算法2——Borderline-SMOTE:【考虑了样本分布,避免新样本受“噪声”点影响】在构造样本时考虑少量样本周围的样本分布,选择少量样本集合(DANGER集合)——其邻居节点 既有多量样本也有少量样本,且多量样本数不大于少量样本的点来构造新样本。
-
改进算法3——KMeans-SMOTE:包括聚类、过滤和过采样三步。利用Kmeans算法完成聚类后,进行样本簇过滤,在每个样本簇内利 用SMOTE算法构建新样本。【样本数量受限制,因为要先找到簇再构建】
-
3. 模型算法
过采样和欠采样都是从样本的层面去克服样本的不平衡,从算法层面来克服样本不平衡。
-
Cost-Sensitive 算法
paper: The Foundations of Cost-Sensitive Learning
代价矩阵 -
MetaCost算法
paper: https://homes.cs.washington.edu/~pedrod/papers/kdd99.pdf “MetaCost”
github: https://github.com/Treers/MetaCost “MetaCost-Python-Coding”
-
在训练集中多次采样,生成多个模型。
-
根据多个模型,得到训练集中每条记录属于 每个类别的概率。
-
计算训练集中每条记录的属于每个类的代价, 根据最小代价,修改类标签。
-
训练修改过的数据集,得到新的模型。

-
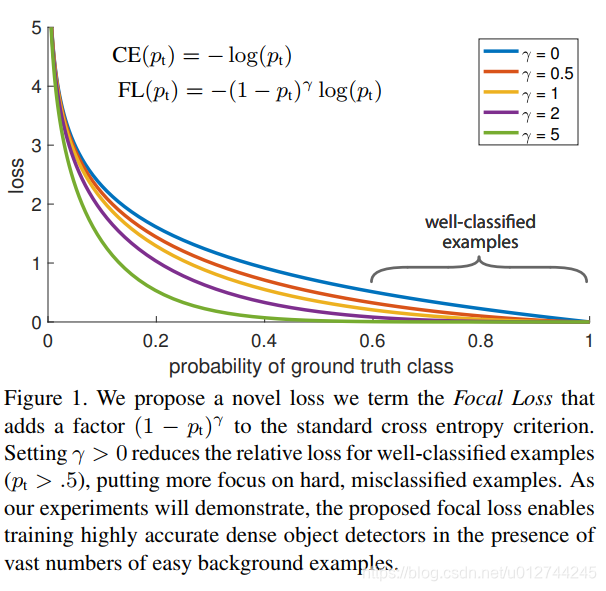
Focal Loss
paper: Focal Loss for Dense Object DetectionFocal loss 是在标准交叉熵损失基础上修改得到的,通过减少易分类样本的权重,使得模型在训练时更专注于难分类的样本。
评价指标
-
基础:混淆矩阵,Recall,Precision,Accuracy,F1
-
衡量不平衡数据:
G − m e a n = T P T P + F N × T N T N + F P G-mean=\sqrt{\frac{TP}{TP+FN}\times\frac{TN}{TN+FP}} G−mean=TP+FNTP×TN+FPTN -
对于多分类问题:Macro,Micro
reference links: F1-score中的Micro和Macro的区别当任务为多分类任务时,Precision和Recall的计算方式就需要权衡每一类的 P r e c i s i o n i Precision_i Precisioni和 R e c a l l i Recall_i Recalli
Macro Micro 适用环境 多分类问题,不受数据不平衡影响,容易受高Recall、高Precision的类别影响。 多分类不平衡问题,若数据极度不平衡影响结果。 使用场景 没有考虑到数据的数量,所以会平等的看待每一类(因为每一类的precision和recall都在0-1之间),会相对受高precision和高recall类的影响较大。 在计算公式中考虑到了每个类别的数量,所以适用于数据分布不平衡的情况;但同时因为考虑到数据的数量,所以在数据极度不平衡的情况下,数量较多数量的类会较大的影响到F1的值。 计算方法 将所有类别的Precision和Recall求平均 计算所有类别的总的Precision和Recall M a c r o P r e c i s i o n = 1 n ∑ i = 1 n P r e c i s i o n i M i c r o P r e c i s i o n = ∑ i = 1 n T P i ∑ i = 1 n T P i + ∑ i = 1 n F P i M a c r o R e c a l l = 1 n ∑ i = 1 n R e c a l l i M i c r o R e c a l l = ∑ i = 1 n T P i ∑ i = 1 n T P i + ∑ i = 1 n F N i M a c r o F 1 = 2 ∗ M a c r o P r e c i s i o n ∗ M a c r o R e c a l l M a c r o P r e c i s i o n + M a c r o R e c a l l M i c r o F 1 = 2 ∗ M i c r o P r e c i s i o n ∗ M i c r o R e c a l l M i c r o P r e c i s i o n + M i c r o R e c a l l MacroPrecision=\frac{1}{n}\sum_{i=1}^{n}Precision_i \qquad MicroPrecision= \frac{\sum_{i=1}^{n}TP_i}{\sum_{i=1}^{n}TP_i + \sum_{i=1}^{n}FP_i}\\ MacroRecall=\frac{1}{n}\sum_{i=1}^{n}Recall_i \qquad MicroRecall=\frac{\sum_{i=1}^{n}TP_i}{\sum_{i=1}^{n}TP_i + \sum_{i=1}^{n}FN_i} \\ MacroF_1=\frac{2*MacroPrecision*MacroRecall}{MacroPrecision + MacroRecall} \qquad MicroF_1=\frac{2*MicroPrecision*MicroRecall}{MicroPrecision + MicroRecall} MacroPrecision=n1i=1∑nPrecisioniMicroPrecision=∑i=1nTPi+∑i=1nFPi∑i=1nTPiMacroRecall=n1i=1∑nRecalliMicroRecall=∑i=1nTPi+∑i=1nFNi∑i=1nTPiMacroF1=MacroPrecision+MacroRecall2∗MacroPrecision∗MacroRecallMicroF1=MicroPrecision+MicroRecall2∗MicroPrecision∗MicroRecall
-
ROC-AUC
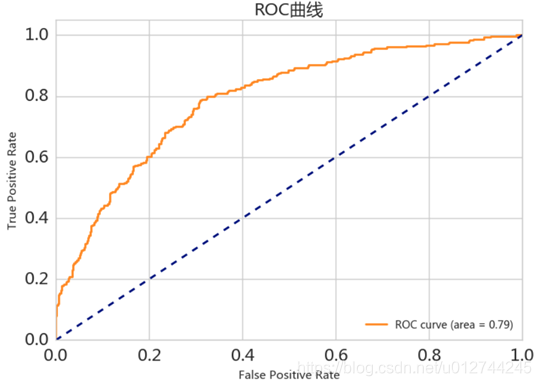
优点:兼顾正例和负例的权衡
- PR-AUC
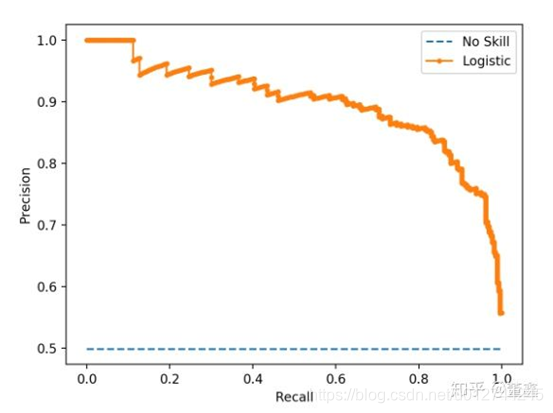
- ROC和PR曲线区别
| ROC | PR | |
|---|---|---|
| 特点 | ROC曲线兼顾正例和负例。在数据不平衡下,ROC曲线具有鲁棒性(稳定),在类别分布发生明显改变时依然能客观识别出较好的分类器。 | 完全聚焦于正例。在数据不平衡下,PR曲线容易受极端的类别数据影响。 |
| 应用场景 | 评估分类器的整体性能:1)当有多份数据且存在不同的类别分布,ROC曲线较适合,可以比较分类器性能且剔除类别分布改变的影响。 | 1)测试不同类别分布下对分类器的性能的影响,PR曲线较适合。2)评估在相同的类别分布下正例的预测情况,PR曲线较适合。 |
类别不平衡问题中,ROC曲线通常会给出一个乐观的效果估计,所以大部分时候还是PR曲线更好。
NLP数据增强
1. UDA (Unsupervised Data Augmentation)【推荐】
paper: Unsupervised Data Augmentation For Consistency Training
github: Unsupervised Data Augmentation
一个半监督的学习方法,减少对标注数据的需求,增加对未标注数据的利用。
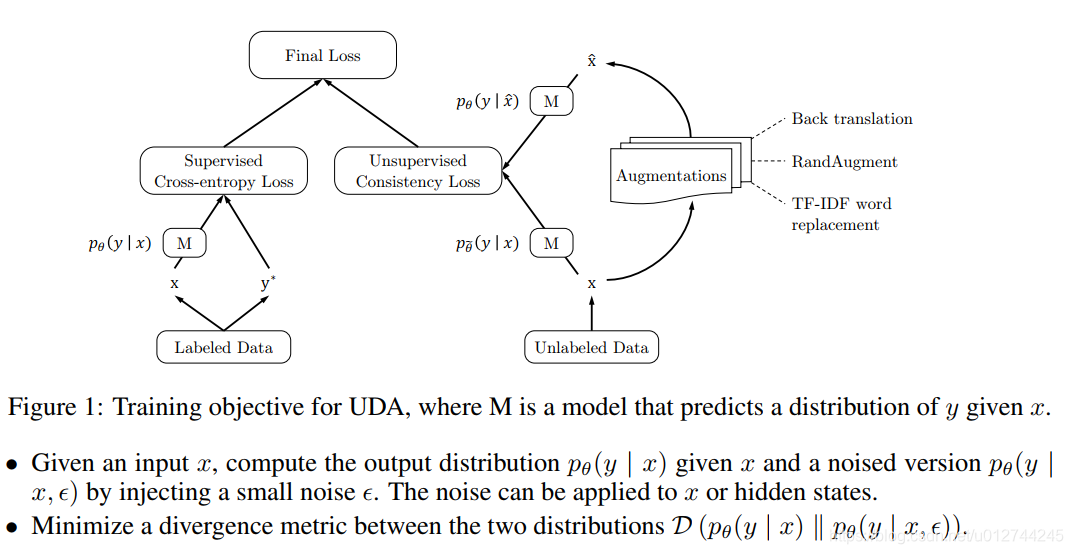

UDA使用的语言增强技术——Back-translation:回译能够在保存语义不变的情况下,生成多样的句式。
关于UDA的文章,有必要阅读并仔细理解,后续会更新。这里先简单给出个人的理解。
UDA关键解决的是如何根据少量的标注数据来增加未标注数据的使用?
对给定的标注数据,可以根据监督学习方法学习到一个模型 M = p θ ( y ∣ x ) M=p_{\theta}(y|x) M=pθ(y∣x)。对未标注数据,进行半监督学习:参考标注数据分布,对未标注数据添加噪声后学习到的模型 p θ ( y ∣ x ^ ) p_{\theta}(y|\hat{x}) pθ(y∣x^)。为了保证一致性的训练(consistency training),需要尽量减少标注数据和未标注数据的分布差异,即最小化两个分布的KL散度: m i n D K L ( p θ ( y ∣ x ) ∣ ∣ p θ ( y ∣ x ^ ) ) min \quad D_{KL} (p_{\theta}(y|x)||p_{\theta}(y|\hat{x})) minDKL(pθ(y∣x)∣∣pθ(y∣x^)) 。而 x ^ = q ( x , ϵ ) \hat{x}=q(x,\epsilon) x^=q(x,ϵ)是对未标注数据添加噪声后得到的增强数据。
那么如何添加噪声 ϵ \epsilon ϵ,来得到增强的数据集 x ^ \hat{x} x^?
文章给出3类noise:
- valid noise: 可以保证原始未标注数据和扩展的未标注数据的预测具有一致性。
- diverse noise: 在不更改标签的情况下对输入进行大量修改,增加样本多样性,而不是仅用高斯噪声进行局部更改。
- targeted inductive biases: 不同的任务需要不同的归纳偏差。
UDA论文中对图像分类、文本分类任务做了实验,分别用到不同的数据增强策略:
- Image Classification: RandAugment
- Text Classification: Back-translation回译,保持语义,利用机器翻译系统进行多语言互译,增加句子多样性。
- Text Classification: Word replacing with TF-IDF ,回译可以保证全局语义不变,但无法控制某个词的保留。对于主题分类任务,某些关键词在确定主题时具有更重要的信息。新的增强方法:用较低的TF-IDF分数替换无信息的单词,同时保留较高的TF-IDF值的单词。
2. EDA (Easy Data Augmentation)
国内中文EDA代码实现:EDA_NLP_for_Chinese
EDA paper:EDA: Easy Data Augmentation Techniques for Boosting Performance on Text Classification Tasks
EDA GitHub:EDA: Easy Data Augmentation Techniques for Boosting Performance on Text Classification Tasks
EDA 的4个数据增强操作:
- 同义词替换(Synonym Replacement, SR):从句子中随机选取n个不属于停用词集的单词,并随机选择其同义词替换它们;
- 随机插入(Random Insertion, RI):随机的找出句中某个不属于停用词集的词,并求出其随机的同义词,将该同义词插入句子的一个随机位置。重复n次;
- 随机交换(Random Swap, RS):随机的选择句中两个单词并交换它们的位置。重复n次;
- 随机删除(Random Deletion, RD):以 p的概率,随机的移除句中的每个单词;
使用EDA需要注意:控制样本数量,少量学习,不能扩充太多,因为EDA操作太过频繁可能会改变语义,从而降低模型性能。
欢迎各位关注我的个人公众号:HsuDan,我将分享更多自己的学习心得、避坑总结、面试经验、AI最新技术资讯。



