- 1SpringBoot整合Kafka
- 2map，split用法,nodejs实现水仙花数_node split map
- 3安装minikube中启动kubectl失败踩坑_failed to run kubelet" err="failed to run kubelet:
- 4【随笔】Git -- 高级命令（下篇）（八）
- 5单片机蜂鸣器音乐代码_51单片机蜂鸣器
- 6axios的介绍与使用_$axios
- 7EXCEL中所有函数的使用_excel 定义相对位置的数组
- 8Ts学习之路-基础篇(可选参数 or 参数默认值)_ts 定义对象设置默认值
- 9软件测试培训分享：软件测试自学能找到工作吗_医疗专业自学软件测试可以找到工作吗
- 10springBoot使用rabbitmq并保证消息可靠性_springboot rabbitmq保证消息不丢失
路径规划算法——基于采样_基于采样的路径规划算法
赞
踩
基于采样的路径规划算法
1.PRM算法
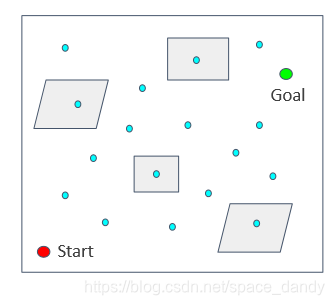
PRM(Probabilistic Road Map)算法，即概率路线图算法是一种融合了采样和图搜索的综合查询方法，该方法首先构建路线图，通过采样和碰撞检测建立完整的无向图，从而得到环境的完整连接属性，然后再通过图搜索得到可行的路径。PRM算法包括学习阶段和查询阶段两部分。
学习阶段 (learning phase)
- 初始化，假设G(V,E)为无向图，顶点集V为环境中无碰撞的节点，E表示无碰撞路径，初始状态设定为空集；
- 采样，从环境空间中采样一个无碰撞的点a(i)加入到顶点集V中；
- 计算邻域，定于距离p，对于已经存在于顶点集V中的点，如果它与a(i)的距离小于p。称其为a(i)的邻域点；
- 边线连接：将a(i)与其邻域点相连，生成连线t；
- 碰撞检测，检测连线t与障碍物是否发生了碰撞，若未发生碰撞，将其加入连线集E中；
- 结束条件，当所有采样点完成上述步骤后结束，否则重复上一步
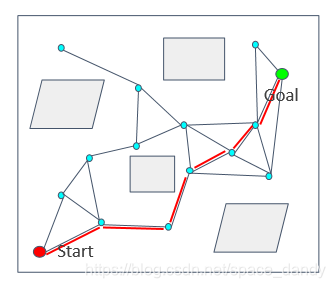
查询阶段 (query phase)
学习阶段建立了无向图，查询阶段使用Dijkstra算法或A*等图搜索算法对无向图G进行搜索，若能找到起始点到终点的路线，表明存在可行的运动规划。
2.RRT(快速搜索随机树)
快速搜索随机树（RRT)算法通过对状态空间中的采样点进行碰撞检测，避免对空间进行建模，可以有效解决高维空间和复杂约束的路径规划问题。该方法是一种增量式采样的搜索方法，可以快速有效地搜索高维空间，通过状态空间的随机采样点，把搜索导向空包区域，从而寻找到一条起始点到目标点的规划路径。
RRT算法思想
RRT以一个初始点作为根节点，通过随机采样增加子节点的方式，生成一个随机扩展树，当随机数的叶子节点包含了目标点或进入了目标区域，便可以在随机树中找到一条由初始点到目标点的路径。具体步骤如下：
- 初始化随机数，仅包含一个根节点 q i n i t q_{init} qinit
- 使用随机采样函数从状态空间随机选择一个采样点 q r a n d q_{rand} qrand
- 使用nearest函数从随机树中选择一个距离 q r a n d q_{rand} qrand最近的节点 q n e a r e s t q_{nearest} qnearest
- 通过扩展函数extend从 q n e a r e s t q_{nearest} qnearest向 q r a n d q_{rand} qrand扩展一段距离，得到新节点 q n e w q_{new} qnew
- 如果 q n e w q_{new} qnew与障碍物发生了碰撞，扩展函数extend返回空值，放弃生长，否则将 q n e w q_{new} qnew加入到随机树
- 充数上述步骤，当 q n e a r e s t q_{nearest} qnearest与目标点 q g o a l q_{goal} qgoal小于一个阈值时，标明随机树到达了目标点
简单的改进
在随机树的每次生长过程中，设置一个随机概念，确定
q
r
a
n
d
q_{rand}
qrand是目标点还是随机点，设置参数prob，每次得到一个0与1之间的随机值p，当0<p<prob，随机树朝目标点生长；当prob<P<1时，随机树朝着随机方向生长。这种方法可以加快随机树到达目标点的速度。
RRT缺点
难以在有狭窄通道的环境找到路径，因为狭窄通道的面积小，被碰到的概率较低
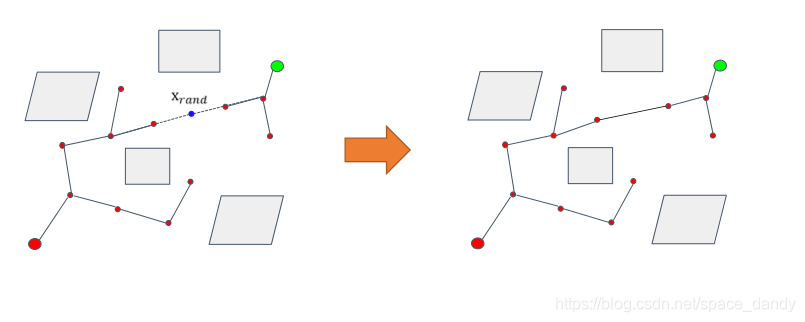
RRT Connect
RRT Connect算法从初始状态点和目标状态点同时生长两棵RRT搜索状态空间。与原始RRT算法相比，该算法在目标点建立了第二棵树，在每次迭代中，开始步骤与原始RRT相同，通过采样随机点进行扩展，在扩展完第一棵树的新节点
q
n
e
w
q_{new}
qnew后，以
q
n
e
w
q_new
qnew为第二棵树的扩展方向，第二棵树的扩展方式略有不同，该算法首先会扩展第一步得到
q
n
e
w
1
q^1_{new}
qnew1，若没有产生碰撞，继续向相同的方向扩展第二步，知道扩展失败或者
q
n
e
w
1
q_{new}^1
qnew1=
q
n
e
w
q_{new}
qnew（表示与第一棵树相连），算法结束。
每次迭代中考虑两棵树的平衡性，即两棵树节点的多少，交换次序小的树进行扩展。
算法代码地址：RRT
3. RRT*
RRT算法不能保证得到的可行路径是相对优化的， R R T ∗ RRT^{*} RRT∗算法针对路径优化问题进行了改进。 R R T ∗ RRT^{*} RRT∗的主要特征是快速找到初始路径，之后随着采样点的增加，不断进行优化直到找到目标点或者设定的最大循环次数。 R R T ∗ RRT^{*} RRT∗算法的收敛时间更长，但计算出路径的代价比RRT算法有所降低，二者的区别主要在于针对新节点 x n e w x_{new} xnew的重计算过程：
- 为 x n e w x_{new} xnew选择父节点的过程与RRT算法相比多了rewire操作
- 重布线随机树
3.1重新选择父节点
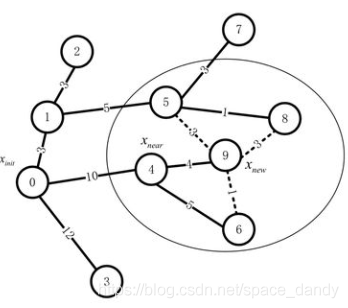
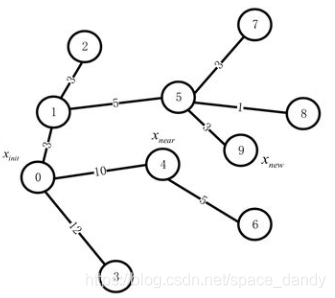
上图表示随机树在扩展过程中的一个时刻，节点上的标号为节点的顺序，节点9为新产生的节点 x n e w x_{new} xnew，节点6为产生节点9的 x n e a r x_{near} xnear(图中标错了)，节点之间连接的边上数字表示两个节点之间的欧氏距离，代表路径代价。
重新选择父节点的过程中，以节点9为圆心，按照事先规定的半径找到圆内的近邻，包括节点4、5、8。原有的0-4-6-9的路径代价和为10+5+1=16；备选的三个节点中，节点5与节点9组成的路径为0-1-5-9，代价和为3+5+3=11；
节点8与节点9组成的路径为0-1-5-8-9，代价和为3+5+1+3=12；节点4与节点9的路径为0-4-9，代价和为10+4=14。
可以看出，如果将节点5作为节点9的新的父节点，路径代价相对最小，因此将节点9的父节点由原来的节点4修改为节点5，生成随机树如下图：
3.2 重新布线随机树
为
x
n
e
w
x_{new}
xnew重新选择父节点后，对随机树进行重新布线可以使得随机树节点间的代价尽量小，即若邻近节点的父节点修改为
x
n
e
w
x_{new}
xnew可以减小路径代价，就对其进行更改。
如下图所示，节点9为新生成的节点
x
n
e
w
x_{new}
xnew，节点4、6、8为其邻近节点，他们的父节点分别为节点0、4、5，构成的路径分别为0-4、0-4-6、0-1-5-8，代价分别为10、15和9。
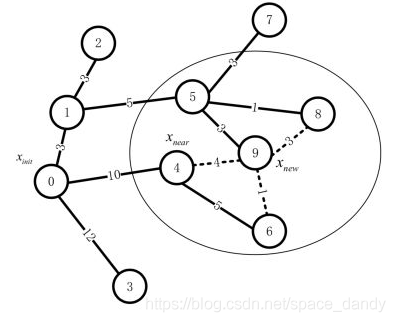
当修改节点4的父节点为节点9时，到达节点为0-1-5-9-4，代价为3+5+3+4大于原来的路径代价10，因此不需要改变节点4的父节点；同理修改节点8的父节点，路径代价将变为14，大于原来的路径代价9，因此不需要修改节点8的父节点；对于节点6，修改其父节点之后，代价为12，小于原来的路径代价，因此将节点6的父节点修改为节点9。由此重新布线后的随机树如下图所示：
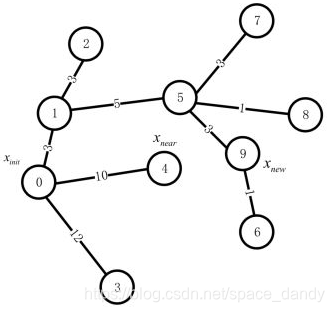
R
R
T
∗
RRT^{*}
RRT∗的核心在于上述的重新选择父节点和重新布线两个过程，重新选择父节点可以使得新生成的节点路径代价尽可能小、重新布线可以使得生成新节点后的随机树减少冗余通路和路径代价，二者相辅相成。
避障策略
对于圆形障碍物，圆形边界的判断属于非线性问题，一般情况下将其转化为多边形进行非线性处理，只需要判断新生成节点
x
n
e
w
x_{new}
xnew的坐标是否是在圆内，如果其位于圆形障碍物的外接正方形内，判断碰撞产生。假设圆形障碍物圆心坐标为(x0,y0)，半径为r，考虑到移动机器人的尺寸，对障碍物进行膨化处理，膨化尺寸为inf，碰撞条件可以表述为：
x
0
−
r
−
i
n
f
<
x
n
e
w
,
x
<
x
0
+
r
+
i
n
f
x_0-r-inf<x_{new,x}<x_0+r+inf
x0−r−inf<xnew,x<x0+r+inf
y
0
−
r
−
i
n
f
<
y
n
e
w
,
y
<
y
0
+
r
+
i
n
f
y_0-r-inf<y_{new,y}<y_0+r+inf
y0−r−inf<ynew,y<y0+r+inf
实际仿真环境中障碍物主要选择为长方形，其碰撞机制需要满足 x n e a r x_{near} xnear与 x n e w x_{new} xnew的连线不能与矩形相交，若二者均位于矩形任意一条边的同侧， 必不相交；若二者分别位于矩形某条边的两侧，则需要进行第二步判断。
若分别位于不同册，有两种情况：
- x n e w x_{new} xnew位于矩形内部，则二者必定相交
- 二者均位于矩形外部，需要利用直线与矩形的性质
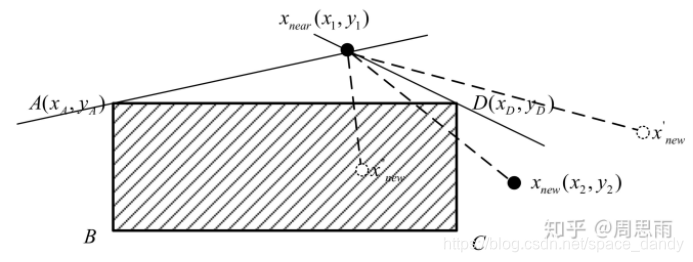
如上图所示，二者均位于AD边两侧且位于矩形外侧，两点连线与矩形相交，
D
x
n
e
a
r
Dx_{near}
Dxnear与
A
x
n
e
a
r
Ax_{near}
Axnear为两个边界，当
x
n
e
a
r
x_{near}
xnear与
x
n
e
w
x_{new}
xnew的连线位于
D
x
n
e
a
r
Dx_{near}
Dxnear与
A
x
n
e
a
r
Ax_{near}
Axnear两条直线的下方时，二者与矩形相交，反正不相交；对于AD边而言，必定发生碰撞的过程可以表述为：
k
x
n
e
a
r
x
n
e
w
<
k
D
x
n
e
a
r
k_{x_{near}x_{new}}<k_{Dx_{near}}
kxnearxnew<kDxnear &&
k
x
n
e
a
r
x
n
e
w
>
k
A
x
n
e
a
r
k_{x_{near}x_{new}}>k_{Ax_{near}}
kxnearxnew>kAxnear
其中k表示直线斜率。
碰撞检测的逻辑如下：
对矩形的一条边设定布尔值b，当b=1时表示发生碰撞；定义判断函数judge(M,N,P),其中：
M
=
(
x
1
,
y
1
)
,
N
=
(
x
2
,
y
2
)
,
P
=
(
x
,
y
)
M=(x_1,y_1),N=(x_2,y_2),P=(x,y)
M=(x1,y1),N=(x2,y2),P=(x,y)
j
u
d
g
e
(
M
,
N
,
P
)
=
(
(
y
−
y
1
)
(
x
2
−
x
1
)
>
(
y
2
−
y
1
)
(
x
−
x
1
)
)
judge(M,N,P)=((y-y_1)(x_2-x_1)>(y_2-y_1)(x-x_1))
judge(M,N,P)=((y−y1)(x2−x1)>(y2−y1)(x−x1))
judge函数为布尔函数，等式右边为真时值为1，否则为0。对于每一条边，其判断逻辑为：
b
=
(
j
u
d
g
e
(
x
n
e
a
r
,
V
e
r
t
e
x
1
,
V
e
r
t
e
x
2
)
!
=
j
u
d
g
e
(
x
n
e
w
,
V
e
r
t
e
x
1
,
V
e
r
t
e
x
2
)
)
b=(judge(x_{near},Vertex_1,Vertex_2)!=judge(x_{new},Vertex_1,Vertex_2))
b=(judge(xnear,Vertex1,Vertex2)!=judge(xnew,Vertex1,Vertex2)) and
(
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
V
e
r
t
e
x
1
)
!
=
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
V
e
r
t
e
x
2
)
)
(judge(x_{near},x_{new},Vertex_1)!=judge(x_{near},x_{new},Vertex_2))
(judge(xnear,xnew,Vertex1)!=judge(xnear,xnew,Vertex2))
V
e
r
t
e
x
i
Vertex_i
Vertexi表示矩形障碍物某一条边的两个定点。
针对前图案例，布尔函数为：
b
1
=
(
j
u
d
g
e
(
x
n
e
a
r
,
A
,
D
)
!
=
j
u
d
g
e
(
x
n
e
w
,
A
,
D
)
)
b_1=(judge(x_{near},A,D)!=judge(x_{new},A,D))
b1=(judge(xnear,A,D)!=judge(xnew,A,D)) and
b
=
(
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
A
)
!
=
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
D
)
)
b=(judge(x_{near},x_{new},A)!=judge(x_{near},x_{new},D))
b=(judge(xnear,xnew,A)!=judge(xnear,xnew,D))
判断逻辑左半部分：
j
u
d
g
e
(
x
n
e
a
r
,
A
,
D
)
=
(
(
y
D
−
y
1
)
(
x
A
−
x
1
)
>
(
y
A
−
y
1
)
(
x
A
−
x
1
)
)
=
0
judge(x_{near},A,D)=((y_D-y_1)(x_A-x_1)>(y_A-y_1)(x_A-x_1))=0
judge(xnear,A,D)=((yD−y1)(xA−x1)>(yA−y1)(xA−x1))=0
j
u
d
g
e
(
x
n
e
w
,
A
,
D
)
=
(
(
y
D
−
y
1
)
(
x
2
−
x
1
)
>
(
y
2
−
y
1
)
(
x
D
−
x
1
)
)
=
1
judge(x_{new},A,D)=((y_D-y_1)(x_2-x_1)>(y_2-y_1)(x_D-x_1))=1
judge(xnew,A,D)=((yD−y1)(x2−x1)>(y2−y1)(xD−x1))=1
因此 ( j u d g e ( x n e a r , A , D ) ! = j u d g e ( x n e w , A , D ) ) = 1 (judge(x_{near},A,D)!=judge(x_{new},A,D))=1 (judge(xnear,A,D)!=judge(xnew,A,D))=1，表示 x n e a r x_{near} xnear与 x n e w x_{new} xnew位于AD边两侧；
判断逻辑右半部分：
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
A
)
=
(
(
y
A
−
y
1
)
(
x
2
−
x
1
)
>
(
y
2
−
y
1
)
(
x
A
−
x
1
)
)
=
0
judge(x_{near},x_{new},A)=((y_A-y_1)(x_2-x_1)>(y_2-y_1)(x_A-x_1))=0
judge(xnear,xnew,A)=((yA−y1)(x2−x1)>(y2−y1)(xA−x1))=0
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
D
)
=
(
(
y
D
−
y
1
)
(
x
2
−
x
1
)
>
(
y
2
−
y
1
)
(
x
D
−
x
1
)
)
=
0
judge(x_{near},x_{new},D)=((y_D-y_1)(x_2-x_1)>(y_2-y_1)(x_D-x_1))=0
judge(xnear,xnew,D)=((yD−y1)(x2−x1)>(y2−y1)(xD−x1))=0
所以
(
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
A
)
!
=
j
u
d
g
e
(
x
n
e
a
r
,
x
n
e
w
,
D
)
)
=
0
(judge(x_{near},x_{new},A)!=judge(x_{near},x_{new},D))=0
(judge(xnear,xnew,A)!=judge(xnear,xnew,D))=0;因此b1=0
综上所述，
x
n
e
a
r
x_{near}
xnear与
x
n
e
w
x_{new}
xnew连线不会与矩形这一条边相交，因此不会发生碰撞。
其他边的判断方法相同，当且仅当
(
b
1
=
0
b1=0
b1=0 and
b
2
=
0
b2=0
b2=0 and
b
3
=
0
b3=0
b3=0 and
b
4
=
0
b4=0
b4=0)=1时，表明
x
n
e
a
r
x_{near}
xnear与
x
n
e
w
x_{new}
xnew与矩形整体不相交。
4.RRT*算法的改进
4.1 Informed RRT*
R
R
T
∗
RRT^*
RRT∗提高规划路径质量的同时，消耗了更长的时间，在保证规划的路径质量的同时，缩短搜索时间是一个探索方向，
I
n
f
o
r
m
e
d
−
R
R
T
∗
Informed-RRT^*
Informed−RRT∗是一个可行的方向。
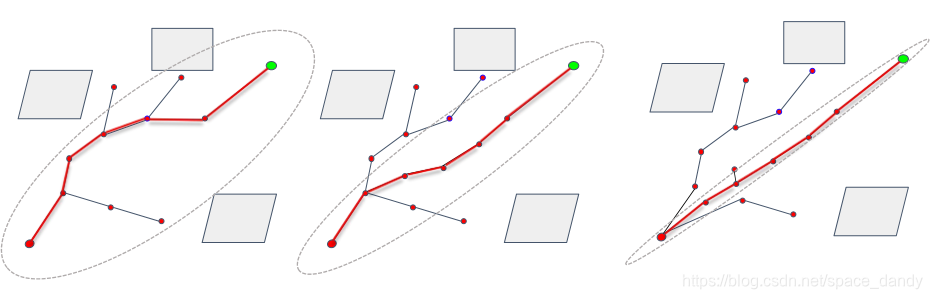
如上图最左侧所示，
R
R
T
∗
RRT*
RRT∗在得到一条可行的路径后，将采样空间限制在一个椭圆形的区域中，并且随着路径长度的不断缩短，逐渐缩小该椭圆形的区域，
I
n
f
o
r
m
e
d
−
R
R
T
∗
Informed-RRT^*
Informed−RRT∗就是对这个椭圆形区域直接采样的方法。算法伪代码如下所示：
伪代码中标红的部分是在
R
R
T
∗
RRT^*
RRT∗基础上进行修改的地方，主要修改内容在第7行采样部分，采样函数的伪代码如下：
采样具体过程如下图所示：
I
n
f
o
r
m
e
d
−
R
R
T
∗
Informed-RRT^*
Informed−RRT∗将目前已经搜索到的最短路径作为
c
b
e
s
t
c_{best}
cbest，起点和终点的距离作为
c
m
i
n
c_{min}
cmin，以此构建椭圆，当没有规划结果时，
c
b
e
s
t
c_{best}
cbest为inf；椭圆中采样涉及到均匀采样方法，是首先在一个单位大小的n维超平面进行采样，然后再映射到超椭球中，具体采样方式见原始论文Informed RRT*
4.2 Cross-entropy motion planning
该算法主要对RRT*采样方式进行了改进，算法思想如下：
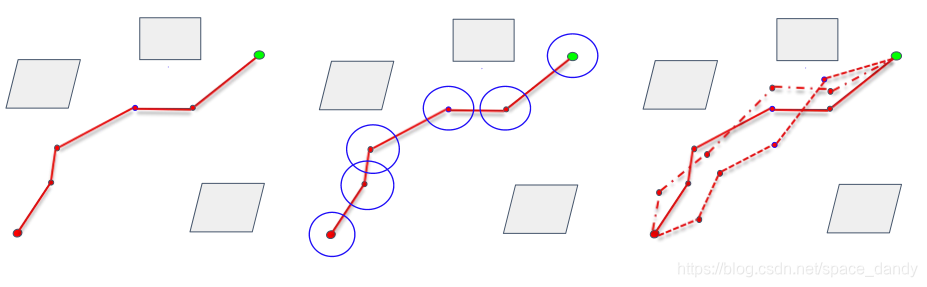
如图所示，首先生成路径，然后在路径的节点附近进行多高斯模型采样，得到更多的路径
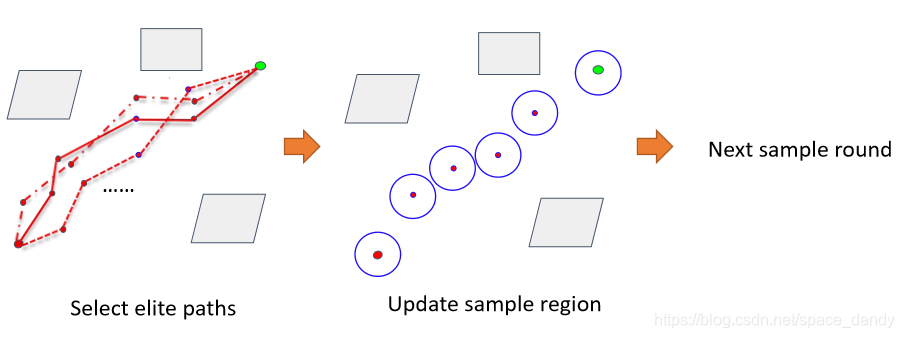
得到更多路径后，算法在更多路径的节点做均值，对均值后的节点重新采样，继续得到更多路径；如此反复。
5.状态栅格搜索器(State Lattice Search)
前述的几种路径搜索算法规划的路径往往没有考虑到机器人的动力学模型，不符合机器人的动力学约束。状态栅格搜索对被控对象进行了运动学模型分析，在此基础上进行路径规划。算法具体思想及理论见下篇State Lattice Search。
参考
[1] https://zhuanlan.zhihu.com/p/65673502
[2] https://www.cnblogs.com/21207-iHome/p/7210543.html
[3] https://zhuanlan.zhihu.com/p/51087819
[4] https://blog.csdn.net/weixin_43890711/article/details/107516647
