dfs与bfs_dfs bfs

深度优先搜素（dfs）

对二叉树尽可能地往节点的终点搜索，只有走到终点才会返回到分叉路口

特点：执着，不撞南墙不回头

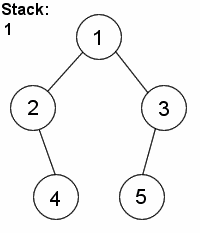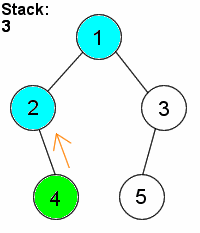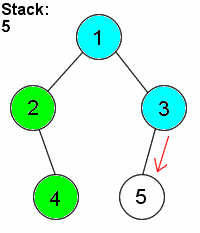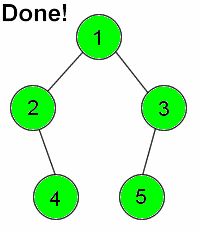
宽度优先搜素（bfs）

对二叉树一层层搜索，只有该层完全搜索完成后才会进行到下一层

特点：稳重，喜欢薅羊毛

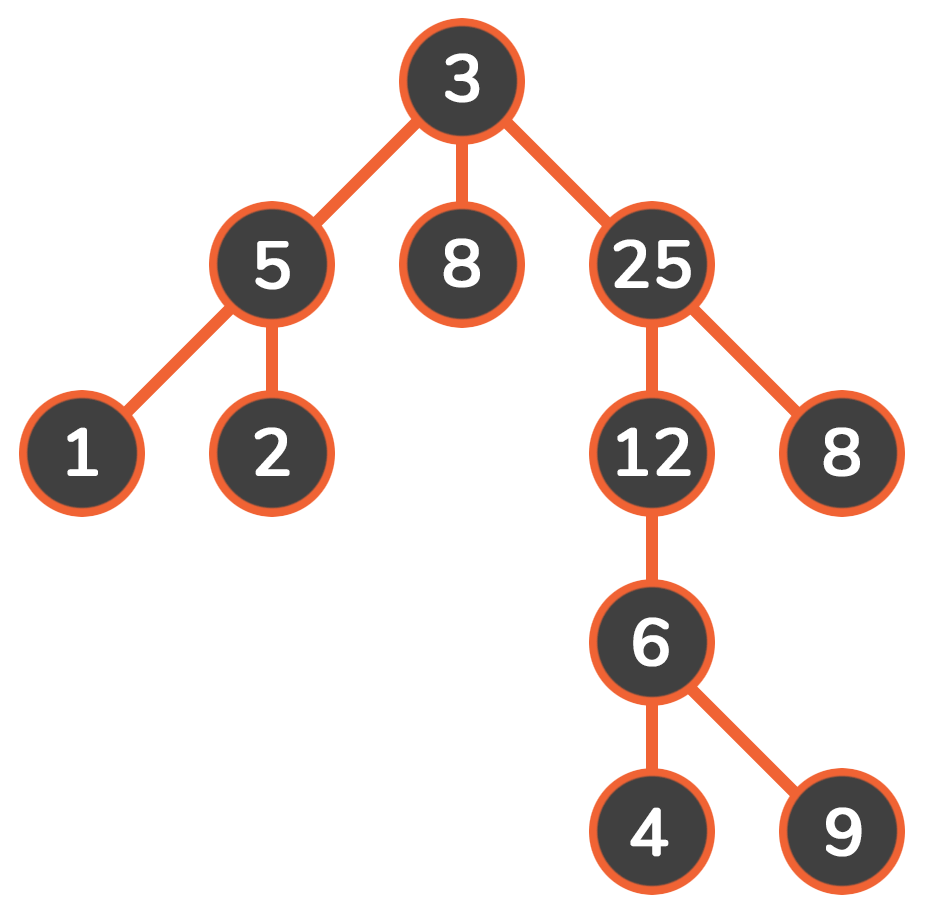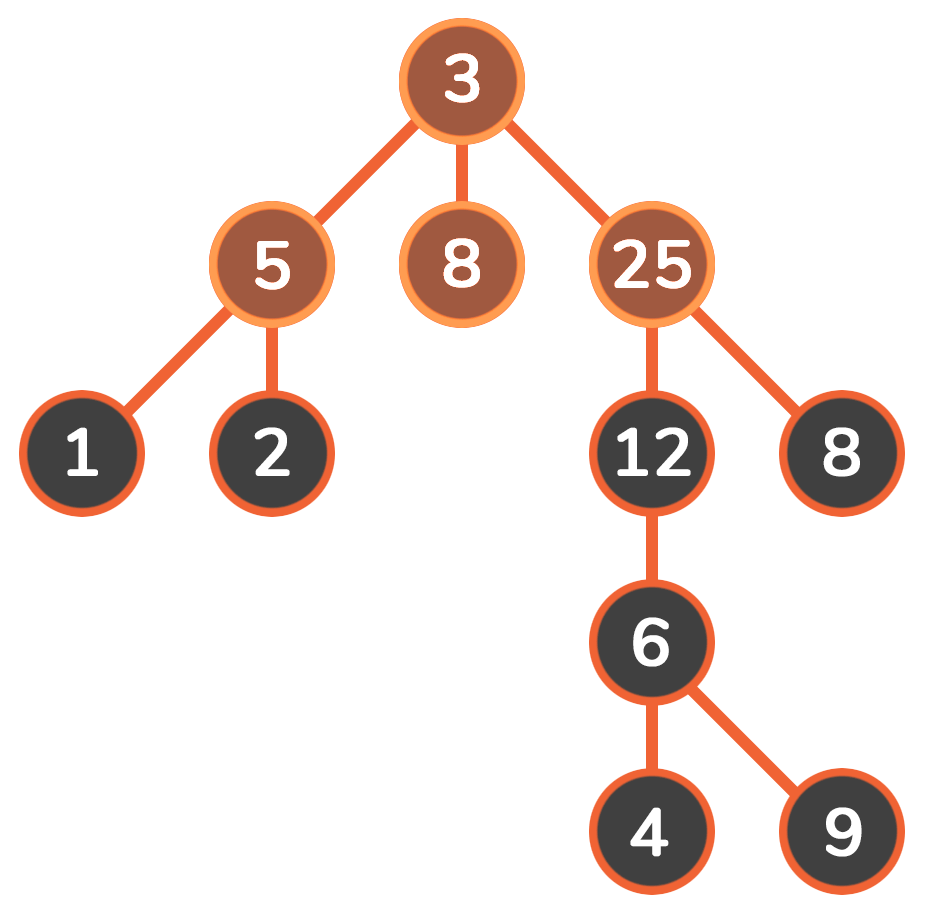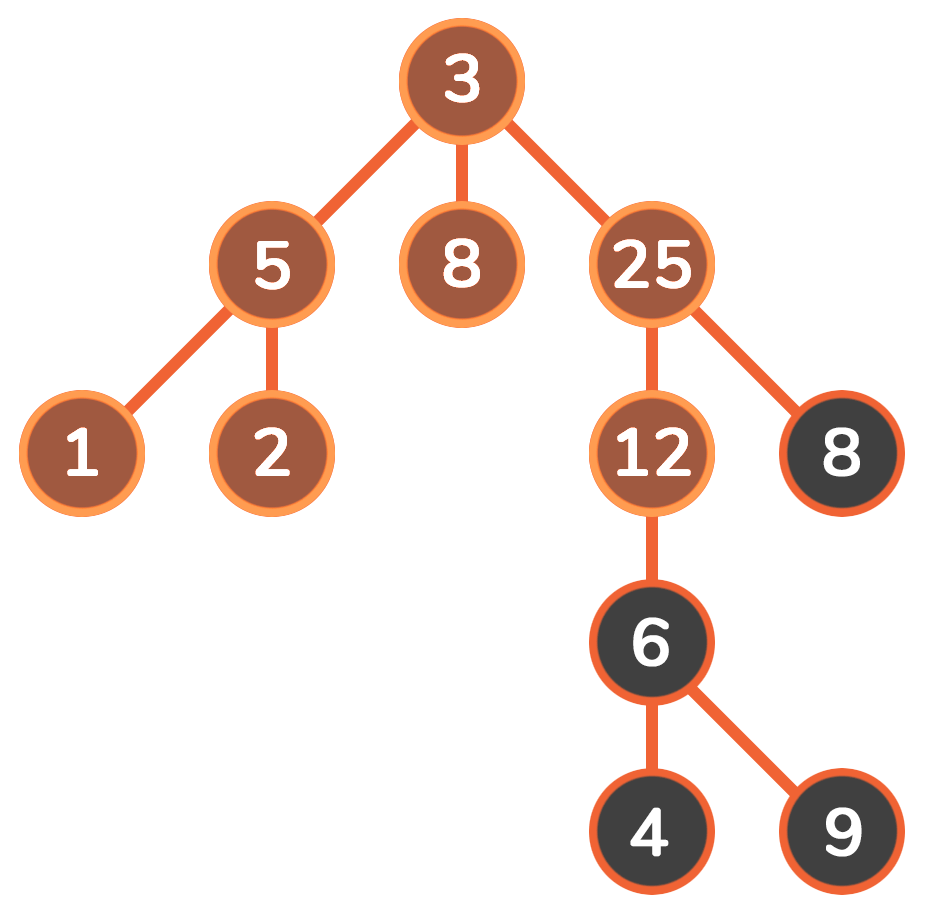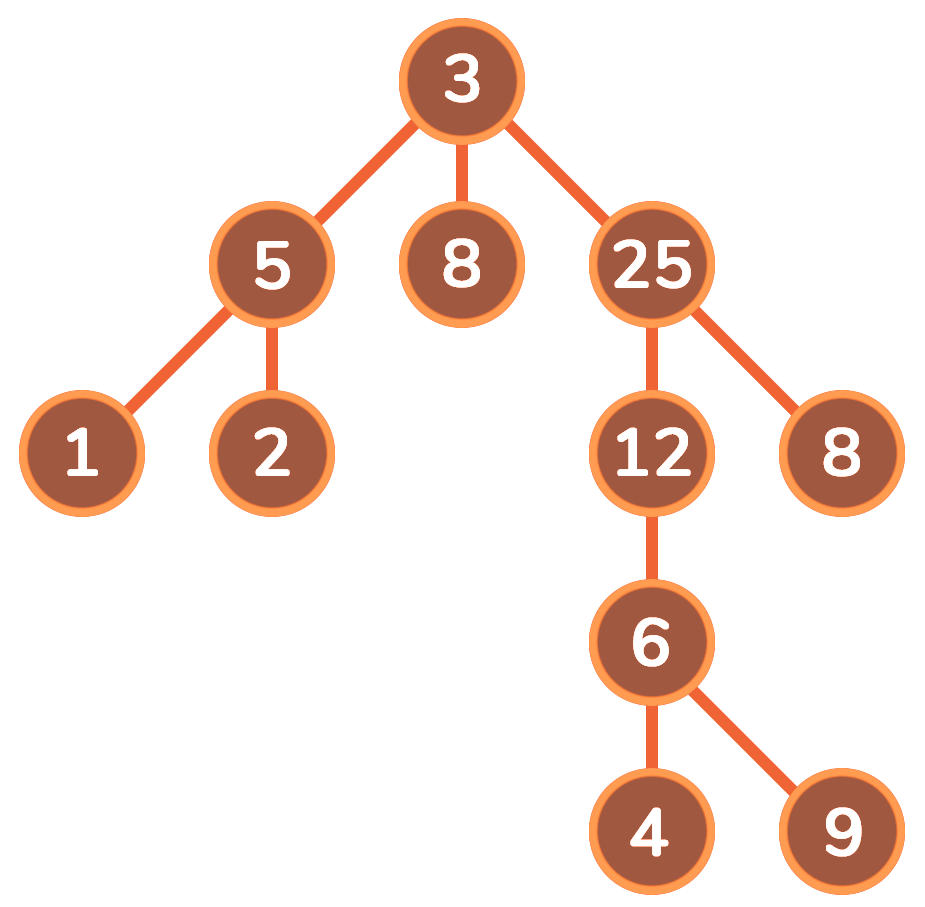
对比

从使用的数据结构来看，dfs使用的是栈，bfs使用的是队列

从使用空间看，dfs只需记录这条路径的所有点，空间复杂度为O（h），bfs记录每层的节点，空间复杂度为O（z ^ h），该特点使bfs有了一个最短路的概念

例题

全排列问题（dfs）

dfs俗称暴搜，他的关键是顺序

题目描述

按照字典序输出自然数 1 到 n 所有不重复的排列，即 n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入格式

一个整数 n。

输出格式

由 1 - n组成的所有不重复的数字序列，每行一个序列。

每个数字保留 5场宽。

样例 #1

样例输入 #1

3
1

样例输出 #1

	1    2    3
    1    3    2
    2    1    3
    2    3    1
    3    1    2
    3    2    1
1
2
3
4
5
6

提示

1≤n≤9。

实现代码

//假设排列1-3
//当你一个数填2时，后面两个的数就不能和前面一样
//如果某一子路径走完了，就需要回溯到上一节点，枚举下一节点
//回溯的同时要记得恢复现场，将改变的变回来
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

const int N = 10;

int n;
int path[N];
bool st[N];//默认为false，如果为true表示该层的某个数被占用
void dfs(int u)//u即层数
{
	if (u == n)//代表path数组填满了，该条路劲走完 
	{
		for (int i = 0;i < n;++i) printf("%5d", path[i]);
		printf("\n");
		return;
	}

	for (int i = 1;i <= n;++i)//排 1 2 3
	{
		if (!st[i])//判断哪个数被占用
		{
			path[u] = i;
			st[i] = true;
			dfs(u + 1);
			st[i] = false;//恢复现场
		}
	}
}
int main()
{
	cin >> n;

	dfs(0);

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

n皇后问题

关键：剪枝，即遇到不合理的情况立刻回溯

输入格式
共一行，包含整数 n。

输出格式
每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围
1≤n≤9
输入样例：

4
1

输出样例：

.Q…
…Q
Q…
…Q.

…Q.
Q…
…Q
.Q…
1
2
3
4
5
6
7
8
9

实现代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

int n;
const int N = 10;
char g[N][N];
bool col[N], dg[N],udg[N];//列，对角线，反对角线
void dfs(int u)
{
	if (u == n)
	{
		for (int i = 0;i < n;++i) printf("%s\n", g[i]);
		return;
	}
	for (int i = 0;i < n;++i)
	{
		if (!col[i] && dg[u + i] && udg[n - u + i])
		{
			g[u][i] = 'Q';
			col[i] = dg[u + i] = udg[n - u + i] = true;
			dfs(u + 1);
			col[i] = dg[u + i] = udg[n - u + i] = false;
		}
	}
}
int main()
{
	cin >> n;
	for (int i = 0; i < n;++i)
	{
		for (int j = 0;j < n;++j)
			g[i][j] = '.';
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

真全排列

//1-9 9个数凑一个等式，其中每个数由3个数字组成
//比如 124 + 659 = 783
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>

using namespace std;

int a[10];
bool st[10];

void dfs(int u)
{
	if (u == 10)
	{
		if (a[1] * 100 + a[2] * 10 + a[3] + a[4] * 100 + a[5] * 10 + a[6] == a[7] * 100 + a[8] * 10 + a[9])//判断是否符合9个数刚好能得到正确结果
			printf("%d%d%d + %d%d%d = %d%d%d\n", a[1], a[2], a[3], a[4], a[5], a[6], a[7], a[8],a[9]);
		return;
	}
	for (int i = 1;i <= 9;++i)
	{
		if (!st[i])
		{
			a[u] = i;
			st[i] = true;
			dfs(u + 1);
			st[i] = false;//恢复现场
		}
	}
}
int main()
{

	dfs(1);//从1开始遍历

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

走迷宫（bfs）

#include <iostream>
#include <queue>
#include <cstring>

using namespace std;
typedef pair<int, int> PII;

int n, m;
const int N = 101;
int g[N][N];//记录图形
int d[N][N];//记录路径数
queue<PII> q;//起始位置

int bfs()
{
	memset(d, -1, sizeof(d));
	d[0][0] = 0;

	q.push({ 0,0 });

	int dx[4] = { 1,0,-1,0 }, dy[4] = { 0,1,0,-1 };

	while (!q.empty())
	{
		PII t = q.front();
		q.pop();

		for (int i = 0; i < 4;++i)
		{
			int x = t.first + dx[i], y = t.second + dy[i];

			if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
			{
				d[x][y] = d[t.first][t.second] + 1;//路径数 + 1
				q.push({x,y});//下一次起始位置
			}
		}
	}

	return d[n - 1][m - 1];
}
int main()
{
	cin >> n >> m;

	for (int i = 0;i < n;++i)
	{
		for (int j = 0;j < m;++j)
			cin >> g[i][j];
	}

	cout << bfs() << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53