线性表 - 栈（数组和链表两种方式实现栈）_栈用链表还是数组存贮

线性表 - 栈（数组和链表两种方式实现栈）

1.1 栈的介绍

• 栈和队列都属于线性数据的逻辑存储结构

• 栈（stack）是一种线性数据结构，栈中的元素只能先入后出（First In Last Out，简称FILO）

• 最早进入的元素存放的位置叫作栈底（bottom），最后进入的元素存放的位置叫作栈顶（top）

• 存储原理
  

  • 栈既可以用数组来实现，也可以用链表来实现

  • 栈的数组实现如下：

    • 数组实现的栈也叫顺序栈或静态栈，链表实现的栈也叫做链式栈或动态栈
    • 栈的链表实现如下：
      

• 操作

  • 入栈（压栈）

    • 入栈操作（push）就是把新元素放入栈中，只允许从栈顶一侧放入元素，新元素的位置将会成为新的栈顶
      
      

  • 出栈（弹栈）

    • 出栈操作（pop）就是把元素从栈中弹出，只有栈顶元素才允许出栈，出栈元素的前一个元素将会成为新的栈顶
      
      

1.2 数组实现栈（顺序栈 / 静态栈）

package com.lagou.entity;

import java.util.Arrays;

/**
 * @author 云梦归遥
 * @date 2022/5/12 17:18
 * @description
 */
public class MyArrayStack {
    private int[] array; //构建的数组对象
    private static final int ARRAY_LENGTH = 8; // 定义无参构造默认的数组长度
    private int length = 0; // 记录数组有效长度

    // 数组构造方法
    public MyArrayStack(){// 默认构造方法数组长度为 8
        this.array = new int[ARRAY_LENGTH];
    }
    public MyArrayStack(int len){// 有参构造则依靠传入的整型数字来构造数组
        this.array = new int[len];
    }

    // 入栈
    public void push(int num){
        array[length++] = num;
    }

    // 出栈
    public int pop(){
        return array[length--];
    }

    // 获取栈顶元素，但不删除栈顶元素
    public int top(){
        return array[length];
    }

    @Override
    public String toString() {
        return "MyArrayStack{" +
                "array=" + Arrays.toString(array) +
                '}';
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

进行测试

package com.lagou.test;

import com.lagou.entity.MyArrayStack;

/**
 * @author 云梦归遥
 * @date 2022/5/12 17:22
 * @description
 */
public class MyArrayStackTest {
    public static void main(String[] args) {
        MyArrayStack stack = new MyArrayStack();
        stack.push(1);
        stack.push(2);
        stack.push(3);
        stack.pop();
        int top = stack.top();
        System.out.println("此时的栈顶元素为：" + top);
        System.out.println("栈：" + stack);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

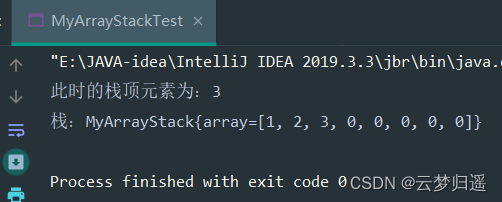
1.3 链表实现栈（链栈 / 动态栈）

package com.lagou.entity;

/**
 * @author 云梦归遥
 * @date 2022/5/12 17:25
 * @description
 */
public class MyLinkStack {
    public class MyLink{
        private int value;
        private MyLink link;

        public MyLink(){
            this.value = 0;
            this.link = null;
        }
        public MyLink(int value){
            this.value = value;
            this.link = null;
        }
        public MyLink(int value, MyLink link){
            this.value = value;
            this.link = link;
        }

        @Override
        public String toString() {
            return "MyLink{" +
                    "value=" + value +
                    ", link=" + link +
                    '}';
        }
    }

    private MyLink head = new MyLink(0, null); // 头结点

    public void push(int num){
        MyLink node = new MyLink(num);
        MyLink temp = head.link; // 创建临时节点吗，进行节点的遍历
        if (head.link == null){
            head.link = node;
        } else {
            while (true){
                if (temp.link == null){
                    break;
                } else {
                    temp = temp.link;
                }
            }
            temp.link = node;
        }
        head.value++; // 链表长度 + 1
    }

    // 出栈
    public int pop(){
        if (head.value == 0){
            return 0;
        } else {
            MyLink temp = head;
            for (int i = 1; i < head.value; i++){
                temp = temp.link;
            }
            MyLink popNode = temp.link;
            temp.link = null;
            head.value--;
            return popNode.value;
        }
    }

    // 只返回栈顶元素，而不让元素出栈
    public int top(){
        if (head.value == 0){
            return 0;
        } else {
            MyLink temp = head;
            for (int i = 1; i < head.value; i++){
                temp = temp.link;
            }
            return temp.link.value;
        }
    }

    // 获取整个栈
    public String select(){
        StringBuilder stringBuilder = new StringBuilder();
        if (head.value == 0){
            return "null";
        } else {
            stringBuilder.append("【栈中元素个数：" + head.value + "】");
            MyLink temp = head;
            for (int i = 1; i < head.value; i++){
                temp = temp.link;
                stringBuilder.append(temp.value + " => ");
            }
            stringBuilder.append(temp.link.value);
            return stringBuilder.toString();
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

进行测试

package com.lagou.test;

import com.lagou.entity.MyLinkStack;

/**
 * @author 云梦归遥
 * @date 2022/5/12 17:40
 * @description
 */
public class MyLinkStackTest {
    public static void main(String[] args) {
        MyLinkStack myLinkStack = new MyLinkStack();
        myLinkStack.push(1);
        myLinkStack.push(2);
        myLinkStack.push(3);
        System.out.println("当前整个栈：" + myLinkStack.select());
        myLinkStack.pop();
        int num = myLinkStack.top();
        System.out.println("当前栈顶元素为：" + num);
        System.out.println("当前整个栈：" + myLinkStack.select());
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

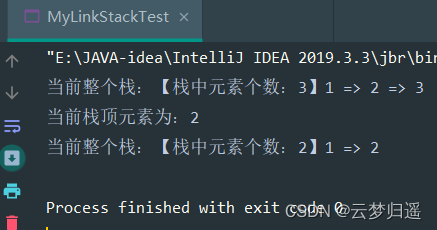
1.4 栈的总结

• 时间复杂度

  • 入栈和出栈的时间复杂度都是O(1)
  • 支持动态扩容的顺序栈
  • 当数组空间不够时，我们就重新申请一块更大的内存，将原来数组中数据统统拷贝过去。这样就实现了
  • 一个支持动态扩容的数组，通过前面学过的知识，可以得知入栈的时间复杂度是O(n)

• 应用

  • 函数调用
    • 每进入一个函数，就会将临时变量作为一个栈入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈
  • 浏览器的后退功能
    • 我们使用两个栈，X 和 Y，我们把首次浏览的页面依次压入栈 X，当点击后退按钮时，再依次从栈X 中出栈，并将出栈的数据依次放入栈 Y。当我们点击前进按钮时，我们依次从栈 Y 中取出数据，放入栈 X 中。当栈 X 中没有数据时，那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据，那就说明没有页面可以点击前进按钮浏览了