热门标签
热门文章
- 12024 Flutter 一季度热门 issue/roadmap 进展和个人感触闲聊
- 2计算机操作系统实验:进程调度实验_操作系统进程调度实验
- 3项目部署阿里云服务器准备工作——最全安装SQLServer 2008教程图解_sql server 2008安装包 阿里云盘
- 4Git第九讲 Git stash暂存消息_git 暂存
- 5element源码学习笔记_elementui 源码学习
- 6深入分析Cocos2d-x 2.0中的“纹理”
- 7micropython esp32驱动舵机_PCA9685舵机控制板与MicroPython-ESP32-1Z实验室
- 8Zookeeper一伪分布式集群搭建_仲裁模式与伪分布式环境搭建头歌
- 9Java 发送邮件,带附件,抄送_java 邮箱 包含 附件、抄送功能么
- 10AI绘画Stable Diffusion | 如何利用SD垫图实现照片风格转换,动漫真人互转教程
当前位置: article > 正文
波士顿房价预测案例(python scikit-learn)---多元线性回归(多角度实验分析)
作者:知新_RL | 2024-05-17 21:30:52
赞
踩
波士顿房价预测
波士顿房价预测案例(python scikit-learn)—多元线性回归(多角度实验分析)
这次实验,我们主要从以下几个方面介绍:
一、相关框架介绍
二、数据集介绍
三、实验结果-优化算法对比实验,数据标准化对比实验,正则化对比试验,多项式回归degree对比实验,岭回归alpha敏感度实验
一、相关框架介绍
Scikit-learn(全称:Simple and Efficient Tools for Machine Learning,意为“简单高效的机器学习工具”)是一个开源的Python机器学习库,它提供了简单而高效的工具,用于数据挖掘和数据分析。
Scikit-learn主要特点包括:丰富的算法库、易于使用、高效的性能、数据预处理和特征选择、模型评估和选择、可扩展性、社区支持。
二、数据集介绍
2.1数据集来源
波士顿房价数据集是一个著名的数据集,它在机器学习和统计分析领域中被广泛用于回归问题的实践和研究。这个数据集包含了美国马萨诸塞州波士顿郊区的房价信息,这些信息是由美国人口普查局收集的。

该数据集共包括507行数据,十三列特征,外加一列标签。
2.2数据集特征
数据集的特征:
CRIM: 城镇人均犯罪率 ZN: 占地面积超过25,000平方英尺的住宅用地比例
INDUS: 每个城镇非零售业务的比例 CHAS: 查尔斯河虚拟变量(如果是河道,则为1;否则为0)
NOX: 一氧化氮浓度(每千万份) RM: 每间住宅的平均房间数
AGE: 1940年以前建造的自住单位比例 DIS: 波士顿的五个就业中心加权距离
RAD: 径向高速公路的可达性指数 TAX: 每10,000美元的全额物业税率
PTRATIO: 城镇的学生与教师比例 B: 1000(Bk - 0.63)^ 2,其中Bk是城镇黑人的比例
LSTAT: 人口状况下降% MEDV: 自有住房的中位数报价, 单位1000美元
三、实验结果-优化算法对比实验,数据标准化对比实验,正则化对比试验,多项式回归degree对比实验,岭回归alpha敏感度实验
3.1 优化算法对比实验
# 从 sklearn.datasets 导入波士顿房价数据读取器。 from sklearn.datasets import load_boston # 从读取房价数据存储在变量 boston 中。 boston = load_boston() # 输出数据描述。 from matplotlib import pyplot as plt from matplotlib import font_manager from matplotlib import pyplot as plt import numpy as np import matplotlib # 参数设置 import matplotlib.pyplot as plt plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体 plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题 # 从sklearn.cross_validation 导入数据分割器。 from sklearn.model_selection import train_test_split # 导入 numpy 并重命名为 np。 import numpy as np from sklearn.linear_model import Ridge,Lasso X = boston.data y = boston.target # 随机采样 25% 的数据构建测试样本,其余作为训练样本。 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25) # 分析回归目标值的差异。 print("The max target value is", np.max(boston.target)) print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target)) # 从 sklearn.preprocessing 导入数据标准化模块。 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import Normalizer # 分别初始化对特征和目标值的标准化器。 ss_X = StandardScaler() ss_y = StandardScaler() ss="StandardScaler" # 分别对训练和测试数据的特征以及目标值进行标准化处理。 X_train = ss_X.fit_transform(X_train) X_test = ss_X.transform(X_test) y_train = ss_y.fit_transform(y_train.reshape(-1, 1)) y_test = ss_y.transform(y_test.reshape(-1, 1)) # 从 sklearn.linear_model 导入 LinearRegression。 from sklearn.linear_model import LinearRegression # 使用默认配置初始化线性回归器 LinearRegression。 def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso = Lasso(alpha=0.01) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model): # 使用 LinearRegression 模型自带的评估模块,并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块,并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块,并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块,并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2): # 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") #plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") #plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01") plt.title("lr,sdgr+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) #plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) #plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列,用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model() models=[lr,sgdr] r2s=[] mess=[] maes=[] nmse=[] results=[] plot_line(X,y,lr,'LinearRegression+'+ss) plot_line(X,y,sgdr,'SGDRegressor+'+ss) #plot_line(X,y,lasso,'lasso'+ss) #plot_line(X,y,ridge,'ridge'+ss) print("sgdr_y_predict") print(sgdr_y_predict) predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict] i=0 for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) plot(results[0][1:4],results[1][1:4])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
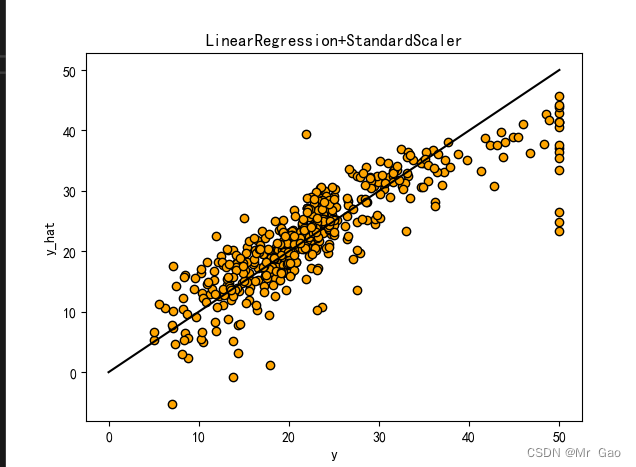
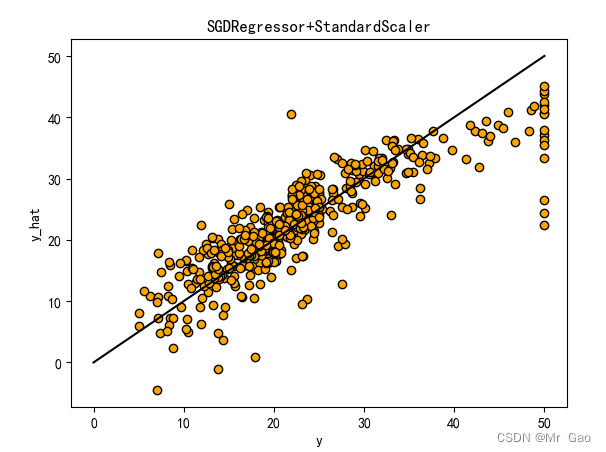
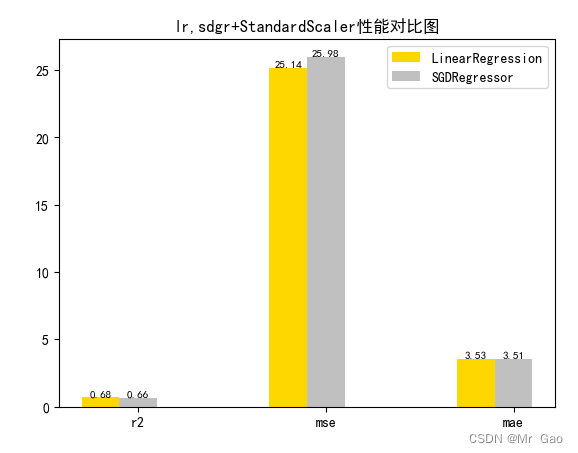
3.2 数据标准化对比实验
# 从 sklearn.datasets 导入波士顿房价数据读取器。 from sklearn.datasets import load_boston # 从读取房价数据存储在变量 boston 中。 boston = load_boston() # 输出数据描述。 from matplotlib import pyplot as plt from matplotlib import font_manager from matplotlib import pyplot as plt import numpy as np import matplotlib # 参数设置 import matplotlib.pyplot as plt plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体 plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题 # 从sklearn.cross_validation 导入数据分割器。 from sklearn.model_selection import train_test_split # 导入 numpy 并重命名为 np。 import numpy as np from sklearn.linear_model import Ridge,Lasso X = boston.data y = boston.target # 随机采样 25% 的数据构建测试样本,其余作为训练样本。 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25) # 分析回归目标值的差异。 print("The max target value is", np.max(boston.target)) print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target)) # 从 sklearn.preprocessing 导入数据标准化模块。 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import Normalizer # 分别初始化对特征和目标值的标准化器。 ss_X = StandardScaler() ss_y = StandardScaler() ss="StandardScaler" # 分别对训练和测试数据的特征以及目标值进行标准化处理。 X_train = ss_X.fit_transform(X_train) X_test = ss_X.transform(X_test) y_train = ss_y.fit_transform(y_train.reshape(-1, 1)) y_test = ss_y.transform(y_test.reshape(-1, 1)) # 从 sklearn.linear_model 导入 LinearRegression。 from sklearn.linear_model import LinearRegression # 使用默认配置初始化线性回归器 LinearRegression。 def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso = Lasso(alpha=0.01) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model): # 使用 LinearRegression 模型自带的评估模块,并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块,并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块,并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块,并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2): # 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") #plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") #plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01") plt.title("lr,sdgr+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) #plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) #plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列,用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model() models=[lr,sgdr] r2s=[] mess=[] maes=[] nmse=[] results=[] plot_line(X,y,lr,'LinearRegression+'+ss) plot_line(X,y,sgdr,'SGDRegressor+'+ss) #plot_line(X,y,lasso,'lasso'+ss) #plot_line(X,y,ridge,'ridge'+ss) print("sgdr_y_predict") print(sgdr_y_predict) predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict] i=0 for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) plot(results[0][1:4],results[1][1:4])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
# 从 sklearn.datasets 导入波士顿房价数据读取器。 from sklearn.datasets import load_boston # 从读取房价数据存储在变量 boston 中。 boston = load_boston() # 输出数据描述。 from matplotlib import pyplot as plt from matplotlib import font_manager from matplotlib import pyplot as plt import numpy as np import matplotlib # 参数设置 import matplotlib.pyplot as plt plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体 plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题 # 从sklearn.cross_validation 导入数据分割器。 from sklearn.model_selection import train_test_split # 导入 numpy 并重命名为 np。 import numpy as np from sklearn.linear_model import Ridge, RidgeCV X = boston.data print(X.min(axis=0)) print(X.max(axis=0)) y = boston.target # 随机采样 25% 的数据构建测试样本,其余作为训练样本。 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25) # 分析回归目标值的差异。 print("The max target value is", np.max(boston.target)) print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target)) # 从 sklearn.preprocessing 导入数据标准化模块。 from sklearn.preprocessing import StandardScaler # 分别初始化对特征和目标值的标准化器。 ss_X = StandardScaler() ss_y = StandardScaler() # 分别对训练和测试数据的特征以及目标值进行标准化处理。 # X_train = ss_X.fit_transform(X_train # X_test = ss_X.transform(X_test) y_train = y_train.reshape(-1, 1) y_test = y_test.reshape(-1, 1) # 从 sklearn.linear_model 导入 LinearRegression。 from sklearn.linear_model import LinearRegression # 使用默认配置初始化线性回归器 LinearRegression。 def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) return lr,sgdr,ridge,lr_y_predict,sgdr_y_predict,ridge_y_predict def evaluate(X_test,y_test,lr_y_predict,model): # 使用 LinearRegression 模型自带的评估模块,并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块,并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块,并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(y_test, lr_y_predict) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块,并输出评估结果。 mae= mean_absolute_error(y_test, lr_y_predict) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2): # 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") # plt.bar(nmse_x,nmse,width=width, color="saddlebrown",label="mse") # plt.bar(mae_x,maes,width=width, color="red",label="mae") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) # plt.text(nmse_x[i],nmse[i], nmse[i],va="bottom",ha="center",fontsize=8) # plt.text(mae_x[i],maes[i], maes[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列,用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,model.predict(X),c="orange",edgecolors='k') print(model.predict(X)) plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lr_y_predict,sgdr_y_predict,ridge_y_predict=train_model() models=[lr,sgdr,] r2s=[] mess=[] maes=[] nmse=[] results=[] plot_line(X,y,lr,'LinearRegression') plot_line(X,y,sgdr,'SGDRegressor') print("sgdr_y_predict") print(sgdr_y_predict) predicts=[lr_y_predict,sgdr_y_predict] i=0 for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) print(results) plot(results[0][1:4],results[1][1:4] )
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
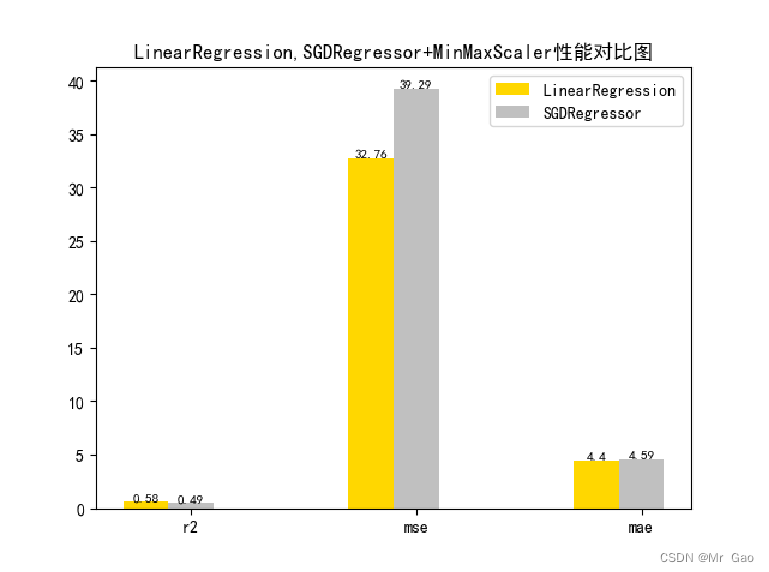
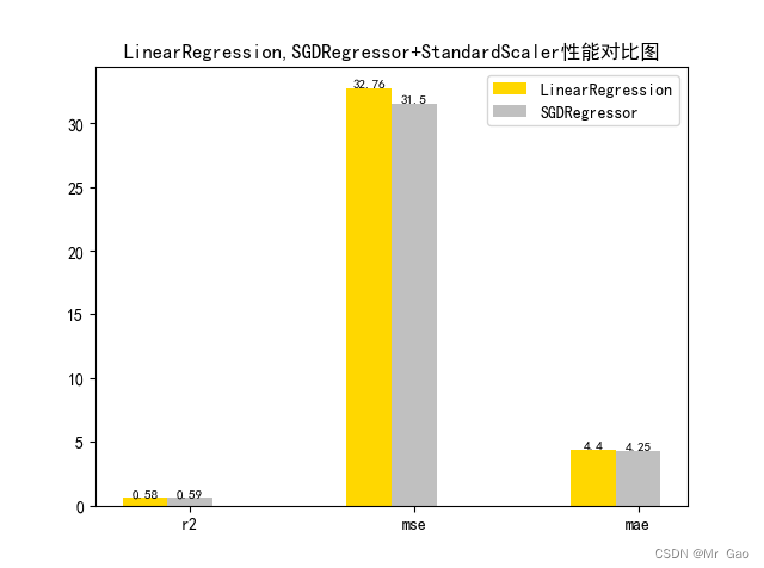

3.3 正则化对比试验
# 从 sklearn.datasets 导入波士顿房价数据读取器。 from sklearn.datasets import load_boston # 从读取房价数据存储在变量 boston 中。 boston = load_boston() # 输出数据描述。 from matplotlib import pyplot as plt from matplotlib import font_manager from matplotlib import pyplot as plt import numpy as np import matplotlib # 参数设置 import matplotlib.pyplot as plt plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体 plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题 # 从sklearn.cross_validation 导入数据分割器。 from sklearn.model_selection import train_test_split # 导入 numpy 并重命名为 np。 import numpy as np from sklearn.linear_model import Ridge,Lasso X = boston.data y = boston.target # 随机采样 25% 的数据构建测试样本,其余作为训练样本。 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25) # 分析回归目标值的差异。 print("The max target value is", np.max(boston.target)) print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target)) # 从 sklearn.preprocessing 导入数据标准化模块。 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import Normalizer # 分别初始化对特征和目标值的标准化器。 ss_X = StandardScaler() ss_y = StandardScaler() ss="StandardScaler" # 分别对训练和测试数据的特征以及目标值进行标准化处理。 X_train = ss_X.fit_transform(X_train) X_test = ss_X.transform(X_test) y_train = ss_y.fit_transform(y_train.reshape(-1, 1)) y_test = ss_y.transform(y_test.reshape(-1, 1)) # 从 sklearn.linear_model 导入 LinearRegression。 from sklearn.linear_model import LinearRegression # 使用默认配置初始化线性回归器 LinearRegression。 def train_model(): lr = LinearRegression() # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = SGDRegressor() # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso = Lasso(alpha=0.01) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model): # 使用 LinearRegression 模型自带的评估模块,并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块,并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块,并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块,并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2,model3,model4): # 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression') plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor") plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01") plt.title("lr,sdgr,lasso,ridge+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model() models=[lr,sgdr,ridge,lasso] r2s=[] mess=[] maes=[] nmse=[] results=[] plot_line(X,y,lr,'LinearRegression+'+ss) plot_line(X,y,sgdr,'SGDRegressor'+ss) plot_line(X,y,lasso,'lasso'+ss) plot_line(X,y,ridge,'ridge'+ss) print("sgdr_y_predict") print(sgdr_y_predict) predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict] i=0 for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
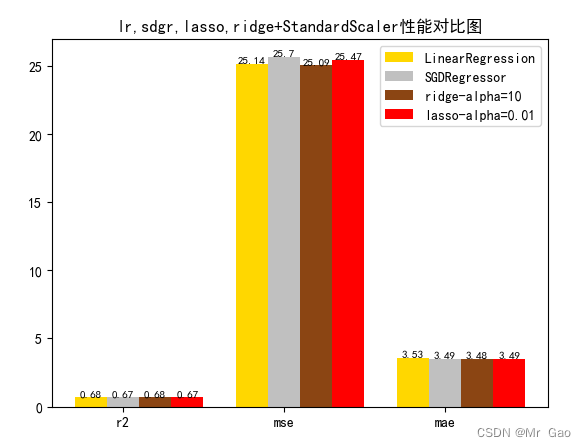
3.4多项式回归degree对比实验
# 从 sklearn.datasets 导入波士顿房价数据读取器。 from sklearn.datasets import load_boston # 从读取房价数据存储在变量 boston 中。 boston = load_boston() # 输出数据描述。 from matplotlib import pyplot as plt from matplotlib import font_manager from matplotlib import pyplot as plt import numpy as np import matplotlib # 参数设置 from sklearn.preprocessing import PolynomialFeatures import matplotlib.pyplot as plt plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体 plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题 # 从sklearn.cross_validation 导入数据分割器。 from sklearn.model_selection import train_test_split # 导入 numpy 并重命名为 np。 import numpy as np from sklearn.linear_model import Ridge,Lasso X = boston.data y = boston.target # 随机采样 25% 的数据构建测试样本,其余作为训练样本。 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25) # 分析回归目标值的差异。 print("The max target value is", np.max(boston.target)) print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target)) # 从 sklearn.preprocessing 导入数据标准化模块。 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import Normalizer # 分别初始化对特征和目标值的标准化器。 ss_X = StandardScaler() ss_y = StandardScaler() ss="StandardScaler" # 分别对训练和测试数据的特征以及目标值进行标准化处理。 X_train = ss_X.fit_transform(X_train) X_test = ss_X.transform(X_test) y_train[0]=y_train[0]+300 y_train = ss_y.fit_transform(y_train.reshape(-1, 1)) y_test = ss_y.transform(y_test.reshape(-1, 1)) # 从 sklearn.linear_model 导入 LinearRegression。 from sklearn.linear_model import LinearRegression # 使用默认配置初始化线性回归器 LinearRegression。 def train_model(): poly_reg = PolynomialFeatures(degree=1) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) # 建模 #lin_reg = LinearRegression().fit(x_poly, y_data) lr = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 poly_reg = PolynomialFeatures(degree=2) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) sgdr = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) poly_reg = PolynomialFeatures(degree=3) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) ridge = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso poly_reg = PolynomialFeatures(degree=4) # 数据转换 x0-->1 x1-->x x2-->x^2 x3-->x^3 x_poly = poly_reg.fit_transform(X_train) lasso = LinearRegression().fit(x_poly, y_train[:,0]) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model): # 使用 LinearRegression 模型自带的评估模块,并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块,并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块,并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块,并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2,model3,model4): # 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='ploy-degree=1') plt.bar(mess_x,model2,width=width,color="silver",label="ploy-degree=2") plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ploy-degree=3") plt.bar(mae_x,model4,width=width, color="red",label="ploy-degree=4") plt.title("不同degree多项式回归+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列,用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model() models=[lr,sgdr,ridge,lasso] r2s=[] mess=[] maes=[] nmse=[] results=[] #plot_line(X,y,lr,'LinearRegression+'+ss) #plot_line(X,y,sgdr,'SGDRegressor'+ss) #plot_line(X,y,lasso,'lasso'+ss) #plot_line(X,y,ridge,'ridge'+ss) print("sgdr_y_predict") print(sgdr_y_predict) predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict] i=0 for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
截图:
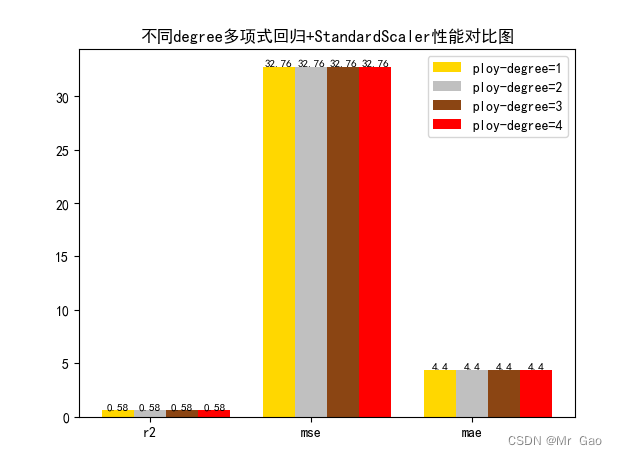
3.5 岭回归alpha敏感度实验
# 从 sklearn.datasets 导入波士顿房价数据读取器。 from sklearn.datasets import load_boston # 从读取房价数据存储在变量 boston 中。 boston = load_boston() # 输出数据描述。 from matplotlib import pyplot as plt from matplotlib import font_manager from matplotlib import pyplot as plt import numpy as np import matplotlib # 参数设置 import matplotlib.pyplot as plt plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体 plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题 # 从sklearn.cross_validation 导入数据分割器。 from sklearn.model_selection import train_test_split # 导入 numpy 并重命名为 np。 import numpy as np from sklearn.linear_model import Ridge,Lasso X = boston.data y = boston.target # 随机采样 25% 的数据构建测试样本,其余作为训练样本。 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25) # 分析回归目标值的差异。 print("The max target value is", np.max(boston.target)) print("The min target value is", np.min(boston.target)) print("The average target value is", np.mean(boston.target)) # 从 sklearn.preprocessing 导入数据标准化模块。 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import Normalizer # 分别初始化对特征和目标值的标准化器。 ss_X = StandardScaler() ss_y = StandardScaler() ss="StandardScaler" # 分别对训练和测试数据的特征以及目标值进行标准化处理。 X_train = ss_X.fit_transform(X_train) X_test = ss_X.transform(X_test) y_train[0]=y_train[0]+300 y_train = ss_y.fit_transform(y_train.reshape(-1, 1)) y_test = ss_y.transform(y_test.reshape(-1, 1)) # 从 sklearn.linear_model 导入 LinearRegression。 from sklearn.linear_model import LinearRegression # 使用默认配置初始化线性回归器 LinearRegression。 def train_model(): lr = Ridge(alpha=2) # 使用训练数据进行参数估计。 lr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lr_y_predict = lr.predict(X_test) # 从 sklearn.linear_model 导入 SGDRegressor。 from sklearn.linear_model import SGDRegressor # 使用默认配置初始化线性回归器 SGDRegressor。 sgdr = Ridge(alpha=5) # 使用训练数据进行参数估计。 sgdr.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 sgdr_y_predict = sgdr.predict(X_test) ridge = Ridge(alpha=10) # 使用训练数据进行参数估计。 ridge.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 ridge_y_predict = ridge.predict(X_test) # Lasso lasso =Ridge(alpha=15) # 使用训练数据进行参数估计。 lasso.fit(X_train, y_train[:,0]) # 对测试数据进行回归预测。 lasso_y_predict = lasso.predict(X_test) return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict def evaluate(X_test,y_test,lr_y_predict,model): # 使用 LinearRegression 模型自带的评估模块,并输出评估结果。 nmse=model.score(X_test, y_test) print('The value of default measurement of LinearRegression is',nmse ) # 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。 from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 使用 r2_score 模块,并输出评估结果。 r2=r2_score(y_test, lr_y_predict) print('The value of R-squared of LinearRegression is',r2 ) # 使用 mean_squared_error 模块,并输出评估结果。 #print(y_test) lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1) #print(lr_y_predict) #print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))) mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean squared error of LinearRegression is',mse ) # 使用 mean_absolute_error 模块,并输出评估结果。 mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)) print('The mean absoluate error of LinearRegression is', mae ) return round(nmse,2),round(r2,2),round(mse,2),round(mae,2) def plot(model1,model2,model3,model4): # 数据 classes = [ 'r2', 'mse', 'mae'] # r2s = [87, 85, 89, 81, 78] # mess = [85, 98, 84, 79, 82] # nmse = [83, 85, 82, 87, 78] # 将横坐标班级先替换为数值 x = np.arange(len(classes)) width = 0.2 r2s_x = x mess_x = x + width nmse_x = x + 2 * width mae_x = x + 3 * width # 绘图 plt.bar(r2s_x, model1, width=width, color='gold', label='ridge-alpha=2') plt.bar(mess_x,model2,width=width,color="silver",label="ridge-alpha=5") plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10") plt.bar(mae_x,model4,width=width, color="red",label="ridge-alpha=15") plt.title("不同alpha-ridge+"+ss+"性能对比图") #将横坐标数值转换为班级 plt.xticks(x + width, classes) #显示柱状图的高度文本 for i in range(len(classes)): plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8) plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8) plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8) plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8) #显示图例 plt.legend(loc="upper right") plt.show() #coding=gbk; def plot_line(X,y,model,name): #-------------------------------------------------------------- #z是我们生成的等差数列,用来画出线性模型的图形。 z=np.linspace(0,50,200).reshape(-1,1) plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k') plt.plot(z,z,c="k") plt.xlabel('y') plt.ylabel("y_hat") plt.title(name) plt.show() lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model() models=[lr,sgdr,ridge,lasso] r2s=[] mess=[] maes=[] nmse=[] results=[] plot_line(X,y,lr,'LinearRegression+'+ss) plot_line(X,y,sgdr,'SGDRegressor'+ss) plot_line(X,y,lasso,'lasso'+ss) plot_line(X,y,ridge,'ridge'+ss) print("sgdr_y_predict") print(sgdr_y_predict) predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict] i=0 for model in models: result=evaluate(X_test,y_test,predicts[i],model) i=i+1 results.append(result) # r2s.append(result[1]) # mess.append(result[2]) # maes.append(result[3]) # nmse.append(result[0]) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) print(results) #evaluate(X_test,y_test,sgdr_y_predict,sgdr) plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
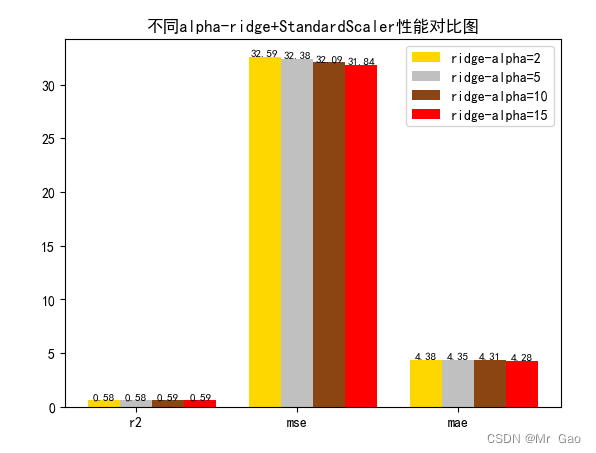
运行结果:
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/知新_RL/article/detail/585339
推荐阅读
相关标签



