红黑树（C语言实现）_c语言红黑树

红黑树（C语言实现）

1. 红黑树的性质

红黑树一共有五点性质：

• 节点是红色或黑色.

• 根是黑色.

• 所有叶子都是黑色（叶子是NIL节点）.

• 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）.

• 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点.

2. 红黑树节点的定义

#define RED				1
#define BLACK 			2

typedef int KEY_TYPE;

typedef struct _rbtree_node {
	unsigned char color;
	struct _rbtree_node *right;
	struct _rbtree_node *left;
	struct _rbtree_node *parent;
	KEY_TYPE key;
	void *value;
} rbtree_node;

typedef struct _rbtree {
	rbtree_node *root;
	rbtree_node *nil;  // 叶子节点都指向nil
} rbtree;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3. 红黑树的旋转

红黑树只有两种旋转：左旋和右旋.
红黑树的旋转只是为了维护红黑树的性质.

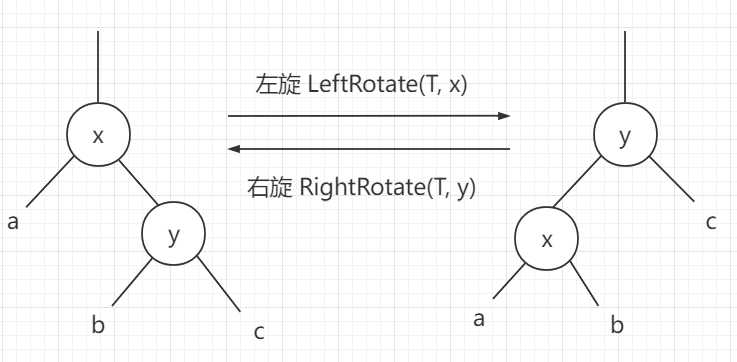
左旋

void rbtree_left_rotate(rbtree *T, rbtree_node *x) {

	rbtree_node *y = x->right;  // x  --> y  ,  y --> x,   right --> left,  left --> right

	x->right = y->left; //1 1
	if (y->left != T->nil) { //1 2
		y->left->parent = x;
	}

	y->parent = x->parent; //1 3
	if (x->parent == T->nil) { //1 4
		T->root = y;
	} else if (x == x->parent->left) {
		x->parent->left = y;
	} else {
		x->parent->right = y;
	}

	y->left = x; //1 5
	x->parent = y; //1 6
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

右旋

void rbtree_right_rotate(rbtree *T, rbtree_node *y) {

	rbtree_node *x = y->left;

	y->left = x->right;
	if (x->right != T->nil) {
		x->right->parent = y;
	}

	x->parent = y->parent;
	if (y->parent == T->nil) {
		T->root = x;
	} else if (y == y->parent->right) {
		y->parent->right = x;
	} else {
		y->parent->left = x;
	}

	x->right = y;
	y->parent = x;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

左旋和右旋在代码上是’‘对称的’'，把左旋代码中的left与right互换、x与y互换，就变成了右旋的代码.

4. 红黑树的插入

4.1 插入操作

红黑树的插入和二叉树的相似，都是如果左子树小，向左子树搜索，否则向右子树搜索.

void rbtree_insert(rbtree *T, rbtree_node *z) {
	
	// 使用快慢指针遍历红黑树，慢指针是快指针的父亲
	rbtree_node *y = T->nil;
	rbtree_node *x = T->root;

	while (x != T->nil) {
		y = x;
		if (z->key < x->key) {
			x = x->left;
		} else if (z->key > x->key) {
			x = x->right;
		} else { // 已经存在key为z->key的节点，直接返回
			return ;
		}
	}

	z->parent = y;
	// 原来的树为空，新插入的节点作为根节点
	if (y == T->nil) {
		T->root = z;
	} else if (z->key < y->key) {
		y->left = z;
	} else {
		y->right = z;
	}

	z->left = T->nil;
	z->right = T->nil;
	// 新插入的节点默认是红色
	z->color = RED;

	// 维护红黑树的性质
	rbtree_insert_fixup(T, z);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

4.2 插入后维护

红黑树新插入的节点默认是红色的，所以当父亲节点也是红色的时候，就会违反第四条性质，我们需要在插入之后做一些调整.

一共会出现三种情况：

1. 插入节点的叔叔节点是红色的

这个时候需要将父节点和叔叔节点都变成黑色，然后把爷爷节点变成红色，然后下一轮迭代就从爷爷节点开始.

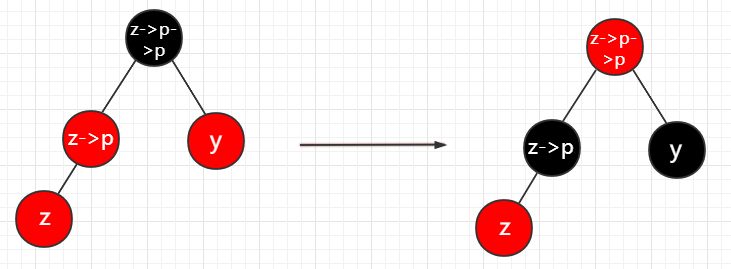
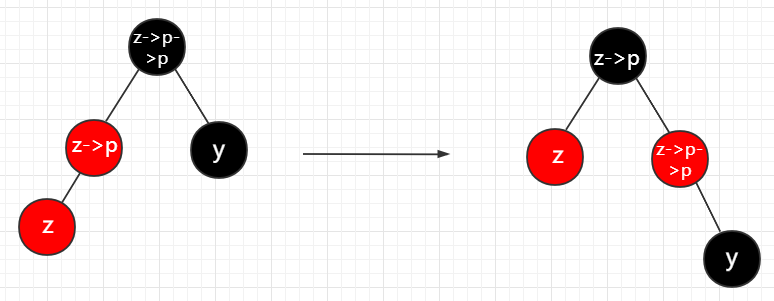
2. 叔叔节点是黑色的，且插入节点是父节点的左孩子

将父节点变成黑色，然后把爷爷节点变成红色，最后绕着爷爷节点做一次右旋.

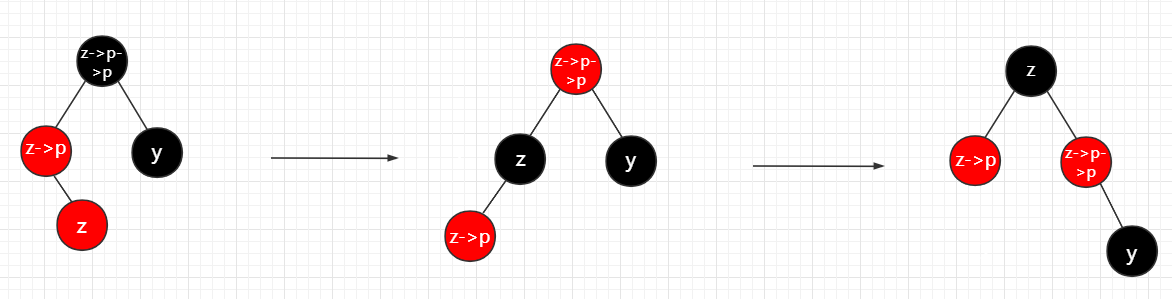
3. 叔叔节点是黑色的，且插入节点是父节点的右孩子

首先绕着父节点做一次左旋，然后将爷爷节点变成红色，父亲节点变成黑色，最后绕着爷爷节点做一次右旋.

void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {

	while (z->parent->color == RED) { //z ---> RED
		if (z->parent == z->parent->parent->left) {
			rbtree_node *y = z->parent->parent->right;
			// 插入节点的叔叔节点是红色
			if (y->color == RED) {
				z->parent->color = BLACK;
				y->color = BLACK;
				z->parent->parent->color = RED;

				z = z->parent->parent; //z --> RED
			} else {
				// 叔叔节点是黑色，且插入节点是父节点的右孩子
				if (z == z->parent->right) {
					z = z->parent;
					rbtree_left_rotate(T, z);
				}

				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rbtree_right_rotate(T, z->parent->parent);
			}
		}else {
			// 插入节点的叔叔节点是红色
			rbtree_node *y = z->parent->parent->left;
			if (y->color == RED) {
				z->parent->color = BLACK;
				y->color = BLACK;
				z->parent->parent->color = RED;

				z = z->parent->parent; //z --> RED
			} else {
				// 叔叔节点是黑色，且插入节点是父节点的左孩子
				if (z == z->parent->left) {
					z = z->parent;
					rbtree_right_rotate(T, z);
				}
		
				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rbtree_left_rotate(T, z->parent->parent);
			}
		}
		
	}

	T->root->color = BLACK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

5. 红黑树的删除

5.1 删除操作

红黑树的删除操作根据儿子节点的孩子节点个数，分为三种情况：

• 没有孩子，即为叶结点。直接把父结点的对应儿子指针设为NULL就可以了.
• 有一个孩子，把父结点的相应儿子指针指向儿子的孩子，然后删除儿子节点就可以了.
• 有两个孩子，用后继节点替换待删除的节点，然后删除这个后继节点，问题就转化成了上述两点.

rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) {

	rbtree_node *y = T->nil;
	rbtree_node *x = T->nil;

	if ((z->left == T->nil) || (z->right == T->nil)) {
		// 儿子节点没有孩子或者只有一个孩子，直接指向这个节点
		y = z;
	} else {
		// 儿子节点有两个孩子，用后继节点替换待删除的节点，问题转化为删除这个后继节点
		y = rbtree_successor(T, z);
	}

	// 如果儿子节点有独生子，那么这个独生子直接继承它爹的位置
	if (y->left != T->nil) {
		x = y->left;
	} else if (y->right != T->nil) {
		x = y->right;
	}

	// 调节继位节点的parent指针指向
	x->parent = y->parent;
	// 调节父节点的孩子指针指向
	if (y->parent == T->nil) {
		// 根节点将被删除，更新根节点
		T->root = x;
	} else if (y == y->parent->left) {
		y->parent->left = x;
	} else {
		y->parent->right = x;
	}
	
	// 如果y是右子树的最小节点，就将y放到z的位置，然后删除原来的z
	if (y != z) {
		z->key = y->key;
		z->value = y->value;
	}

	// 如果删除的节点是黑色的，就要维护一下红黑树的性质
	if (y->color == BLACK) {
		rbtree_delete_fixup(T, x);
	}

	return y;
}

// 找右子树中的最小节点
rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
	while (x->left != T->nil) {
		x = x->left;
	}
	return x;
}

// 找左子树中的最大节点
rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {
	while (x->right != T->nil) {
		x = x->right;
	}
	return x;
}

rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x) {
	rbtree_node *y = x->parent;
	// 后继节点就是中序遍历时右子树的第一个节点
	if (x->right != T->nil) {
		return rbtree_mini(T, x->right);
	}

	// 这里应该不会被执行到，因为此时的待删除节点必然有两个孩子节点
	// 如果没有右子树，那就是作为左子树时的根节点
	while ((y != T->nil) && (x == y->right)) {
		x = y;
		y = y->parent;
	}
	return y;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

5.2 删除后维护

如果要删除节点是黑色的（破坏了黑高），就需要维护一下红黑树的性质，对应的一共有四种情况：

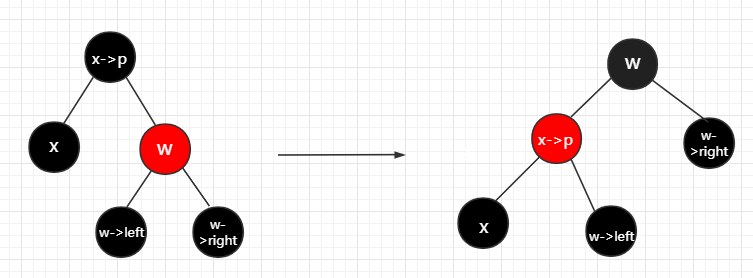
1. x的兄弟节点w是红色的

将w涂黑，将x->p涂红，然后把兄弟节点绕着父节点左旋，最后把w重新做指向，令w=x->p->right，这样w变成了黑色结点（根据红黑树的性质，必定是黑色的），调整结束以后，情况1可能会变成情况2、3、4.

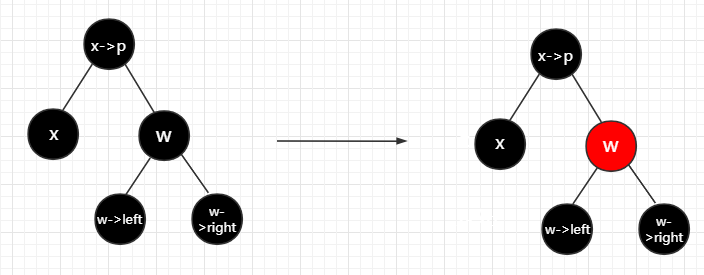
2. x的兄弟w是黑色的，且w的两个儿子都是黑色

直接把兄弟节点变成红色，再将指向x的指针指向父节点，然后根据父亲节点的颜色决定是否进行下一步调整，如果父亲节点的颜色为红色，就把父亲节点变成黑色，即可结束调整；如果父亲节点的颜色是黑色，那就要根据调整结束后的状态做下一步调整，可能会变成情况1、2、3、4.

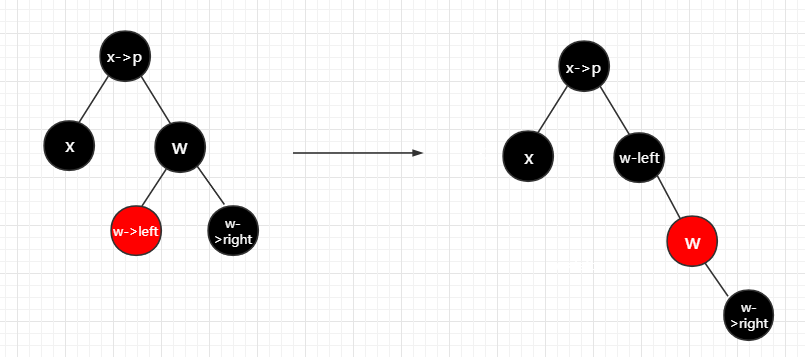
3. x的兄弟w是黑色的，而w的左孩子为红色，右孩子为黑色

那么我们将w->left涂黑，然后将w涂红，再将w->left绕着w做右旋，然后情况3就会变成情况4.

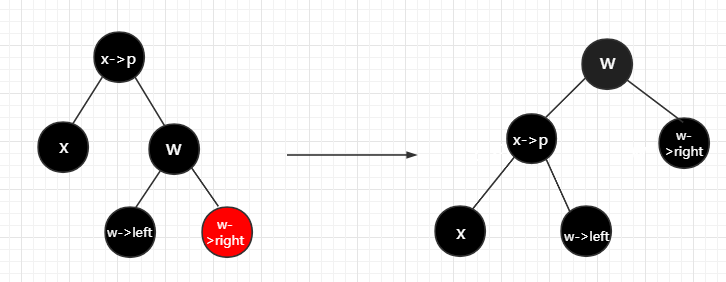
4. x的兄弟w是黑色的，而w的左孩子为黑色，右孩子为红色

把兄弟节点w换成父节点的颜色，并把父亲节点和w-right涂黑，然后把兄弟节点w绕着父节点做一次左旋，完成之后的结构刚好满足红黑树的性质.

void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {

	while ((x != T->root) && (x->color == BLACK)) {
		// 此if与相应的else是镜像的
		if (x == x->parent->left) {
			// 找到兄弟节点
			rbtree_node *w= x->parent->right;
			// 情况1：兄弟节点为红色
			if (w->color == RED) {
				// 兄弟节点变成黑色
				w->color = BLACK;
				// 父节点变成红色
				x->parent->color = RED;
				
				// 父节点做左旋
				rbtree_left_rotate(T, x->parent);
				// 重新设置x的兄弟节点
				w = x->parent->right;
			}
				// 情况2：兄弟节点是黑色的，且兄弟的左孩子和右孩子都是黑色
			if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
				//  兄弟节点变成红色
				w->color = RED;
				// 将指向x的指针指向其父节点
				x = x->parent;
			} else {
				// 情况3：x的兄弟节点是黑色的，兄弟的左孩子是红色，右孩子是黑色
				if (w->right->color == BLACK) {
					// 将左孩子涂黑
					w->left->color = BLACK;
					// 将兄弟节点变红
					w->color = RED;
					// 对兄弟节点右旋
					rbtree_right_rotate(T, w);
					// 重新设置x的兄弟节点
					w = x->parent->right;
				}
				// 情况4：x的兄弟节点是黑色；x的兄弟节点的右孩子是红色的
				// 将兄弟节点换成父节点的颜色
				w->color = x->parent->color;
				// 把父节点和兄弟节点的右孩子涂黑
				x->parent->color = BLACK;
				w->right->color = BLACK;
				// 对父节点做左旋
				rbtree_left_rotate(T, x->parent);
				// 设置x指针，指向根节点
				x = T->root;
			}

		} else {

			rbtree_node *w = x->parent->left;
			if (w->color == RED) {
				w->color = BLACK;
				x->parent->color = RED;
				rbtree_right_rotate(T, x->parent);
				w = x->parent->left;
			}

			if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
				w->color = RED;
				x = x->parent;
			} else {

				if (w->left->color == BLACK) {
					w->right->color = BLACK;
					w->color = RED;
					rbtree_left_rotate(T, w);
					w = x->parent->left;
				}

				w->color = x->parent->color;
				x->parent->color = BLACK;
				w->left->color = BLACK;
				rbtree_right_rotate(T, x->parent);

				x = T->root;
			}
		}
	}
	// 继承节点变为黑色，为了弥补失去的黑高
	x->color = BLACK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

6. 查找节点

红黑树的查找与普通二叉树的查找是一样的：

rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {

	rbtree_node *node = T->root;
	while (node != T->nil) {
		if (key < node->key) {
			node = node->left;
		} else if (key > node->key) {
			node = node->right;
		} else {
			return node;
		}	
	}
	return T->nil;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

7. 红黑树的遍历

红黑树的遍历也与普通二叉树的遍历是一样的，这里只展示递归版的中序遍历：

void rbtree_traversal(rbtree *T, rbtree_node *node) {
	if (node != T->nil) {
		rbtree_traversal(T, node->left);
		printf("key:%d, color:%d\n", node->key, node->color);
		rbtree_traversal(T, node->right);
	}
}
1
2
3
4
5
6
7

8. 展示

int main() {

	int keyArray[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};

	rbtree *T = (rbtree *)malloc(sizeof(rbtree));
	if (T == NULL) {
		printf("malloc failed\n");
		return -1;
	}
	
	T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
	T->nil->color = BLACK;
	T->root = T->nil;

	rbtree_node *node = T->nil;
	int i = 0;
	for (i = 0;i < 20;i ++) {
		node = (rbtree_node*)malloc(sizeof(rbtree_node));
		node->key = keyArray[i];
		node->value = NULL;

		rbtree_insert(T, node);
		
	}

	rbtree_traversal(T, T->root);
	printf("----------------------------------------\n");

	for (i = 0;i < 20;i ++) {

		rbtree_node *node = rbtree_search(T, keyArray[i]);
		rbtree_node *cur = rbtree_delete(T, node);
		free(cur);

		rbtree_traversal(T, T->root);
		printf("----------------------------------------\n");
	}
	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39