机器学习之PyTorch和Scikit-Learn第3章 使用Scikit-Learn的机器学习分类器之旅Part 2_pycharm中使用sklearn svm中分类器

其它章节内容请见机器学习之PyTorch和Scikit-Learn

支持向量机实现最大间隔分类

另一种强大又广泛使用的学习算法是支持向量机(SVM)，可看成是对感知机的扩展。使用感知机算法，我们最小化误分类错误。但在SVM中，我们的优化目标是最大化间隔（margin）。间隔定义为分隔的超平面（决策边界）之间的距离，距离超平面最近的训练样本称为支持向量。

如图3.10所示：

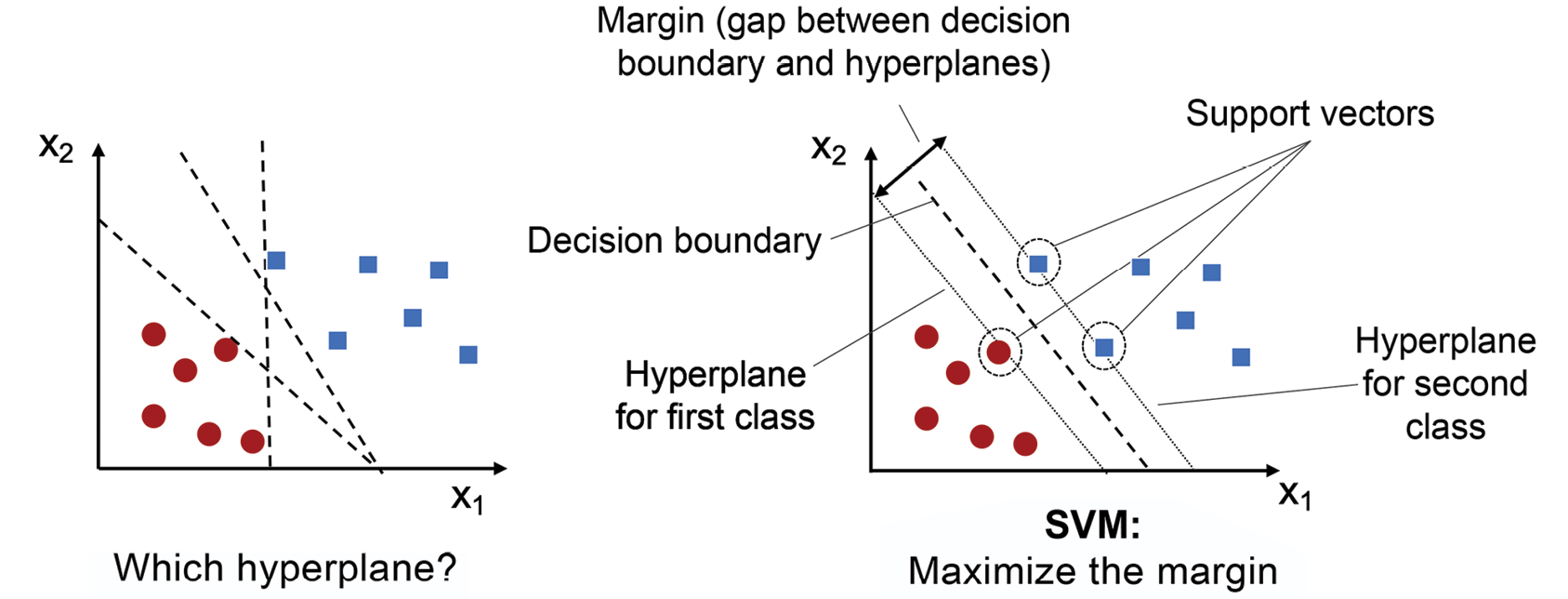
图3.10：SVM最大化决策边界与训练数据点之间的间距

最大间隔构想

让决策边界具有大间隔背后的根本原因是那样会趋向更低的泛化错误，而具有小间隔的模型更容易出现过拟合。

虽然SVM背后的主要构想相对简单，但不幸的是背后的数据很高阶，要求对约束最优化有很好的掌握。

因此，SVM中最大间隔优化的细节不在本书的范畴内。但我们为有志了解更多的读者推荐如下资源：

• Chris J.C. Burges在A Tutorial on Support Vector Machines for Pattern Recognition 一书中很优秀的讲解(Data Mining and Knowledge Discovery, 2(2): 121-167, 1998)
• Vladimir Vapnik所著The Nature of Statistical Learning Theory, Springer Science+Business Media, Vladimir Vapnik, 2000
• 吴恩达非常详细的授课笔记https://see.stanford.edu/materials/aimlcs229/cs229-notes3.pdf

使用松弛变量处理线性不可分割案例

虽然我们不希望深度介入最大间隔分类背后的数据概念，但还是要简单讲解一下松弛变量（slack variable），它由Vladimir Vapnik于1995年引入并产生了所谓的软间隔分类（soft-margin classification）。引入松弛变量的动机是SVM优化目标中的线性约束需要松弛线性不可分割数据来在出现错误分类时使用合适的损失惩罚实现优化的收敛。

而松弛变量的使用，又引入了SVM上下文中经常被称为C的变量。可以把C看成是控制错误分类处罚的超参数。大值的C对应大的错误惩罚，而如果选择小值的C则表示对错误分类误差没那么严格。然后我们可以使用参数C来控制间隔宽度，因而调优偏差-方差均衡，如图3.11所示：

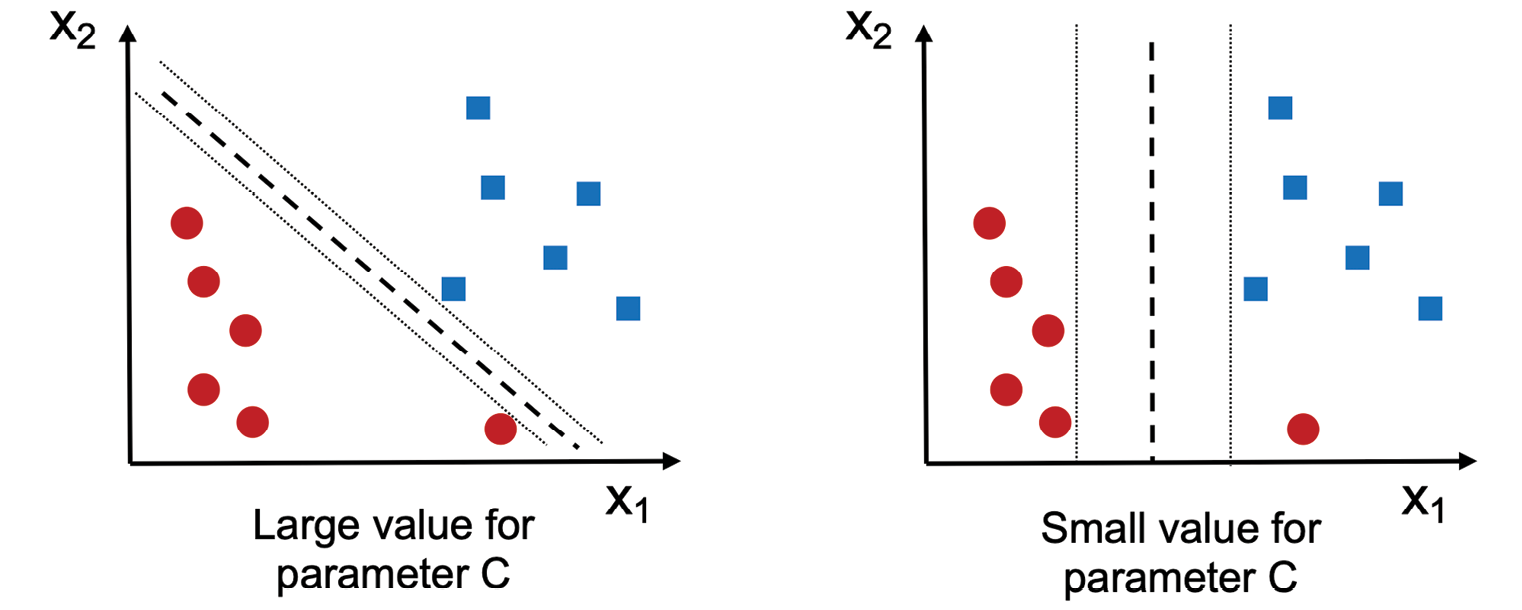
图3.11：分类上翻转正则化强度C大小值的影响

这一概念与正则化相关，我们在前一节的正则化回归上下文中讨论过，减小C的值会增加偏差（欠拟合）及降低模型的方差（过拟合）。

既然我们已经学习了线性支持向量机背后的基本概念，下面来训练SVM模型对鸢尾花中不同的花：

>>> from sklearn.svm import SVC
>>> svm = SVC(kernel='linear', C=1.0, random_state=1)
>>> svm.fit(X_train_std, y_train)
>>> plot_decision_regions(X_combined_std,
...                       y_combined,
...                       classifier=svm,
...                       test_idx=range(105, 150))
>>> plt.xlabel('Petal length [standardized]')
>>> plt.ylabel('Petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

SVM的三个决策区域，在执行以上示例代码对鸢尾花训练分类器可视化为图3.12：

图3.12：SVM的决策区域

逻辑回归 vs. SVM

在实际分类任务中，线性逻辑回归与线性SVM经常产生非常相似的结果。逻辑回归尝试最大化训练数据的条件似然，这会比SVM更容易接近异常值，后者更关心的是最接近决策边界（支持向量）的那些点。另一方面，逻辑回归的优势是模型更简单、实现更容易，并且在数学上也更容易解释。此外，逻辑回归模型可以很易于更新，这对于处理流式数据很有吸引力。

scikit-learn中的替代实现

上一节中我们使用的scikit-learn库的LogisticRegression类，可通过设置solver='liblinear'来利用LIBLINEAR库。LIBLINEAR是台湾大学开发的高度优化的C/C++库(http://www.csie.ntu.edu.tw/~cjlin/liblinear/)。

类似地，用于训练支持向量机的SVC类利用了LIBSVM，这是一个等价的专门用于SVM的C/C++库(http://www.csie.ntu.edu.tw/~cjlin/libsvm/)。

使用LIBLINEAR和LIBSVM的优势，比如相比原生Python实现来说，它们使训练大量的线性分类器变得极其快速。但有时数据集过大电脑内存无法容纳。因此scikit-learn还提供了通过SGDClassifier类的一些替代实现，该类还支持通过partial_fit方法进行的在线学习。SGDClassifier背后的概念类似于我们在第2章中为Adaline所实现的随机梯度算法。

我们可以初始化SGD版本的感知机(loss='perceptron')、逻辑回归(loss='log')及带默认参数的SVM(loss='hinge')，如下：

>>> from sklearn.linear_model import SGDClassifier
>>> ppn = SGDClassifier(loss='perceptron')
>>> lr = SGDClassifier(loss='log')
>>> svm = SGDClassifier(loss='hinge')
1
2
3
4

使用核函数SVM解决非线性问题

SVM在机器学习从业者中知名度很高的另一个原因是，很容易将它们核化（kernelized）来解决非线性分类问题。在讨论最常见SVM的变体核SVM背后的主要概念之前，我们先创建一个人工数据集来看这种非线性分类问题是什么样的。

线性不可分割数据的核方法

使用如下代码，我们会使用NumPy中的logical_xor函数创建异或门（XOR）形式的简单数据集，其中100个样式会被赋类标签1，100个样本会被赋类标签-1：

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> np.random.seed(1)
>>> X_xor = np.random.randn(200, 2)
>>> y_xor = np.logical_xor(X_xor[:, 0] > 0,
...                        X_xor[:, 1] > 0)
>>> y_xor = np.where(y_xor, 1, 0)
>>> plt.scatter(X_xor[y_xor == 1, 0],
...             X_xor[y_xor == 1, 1],
...             c='royalblue', marker='s',
...             label='Class 1')
>>> plt.scatter(X_xor[y_xor == 0, 0],
...             X_xor[y_xor == 0, 1],
...             c='tomato', marker='o',
...             label='Class 0')
>>> plt.xlim([-3, 3])
>>> plt.ylim([-3, 3])
>>> plt.xlabel('Feature 1')
>>> plt.ylabel('Feature 2')
>>> plt.legend(loc='best')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

执行这段代码，我们会得到一随机噪声的异或数据集，如图3.13所示：

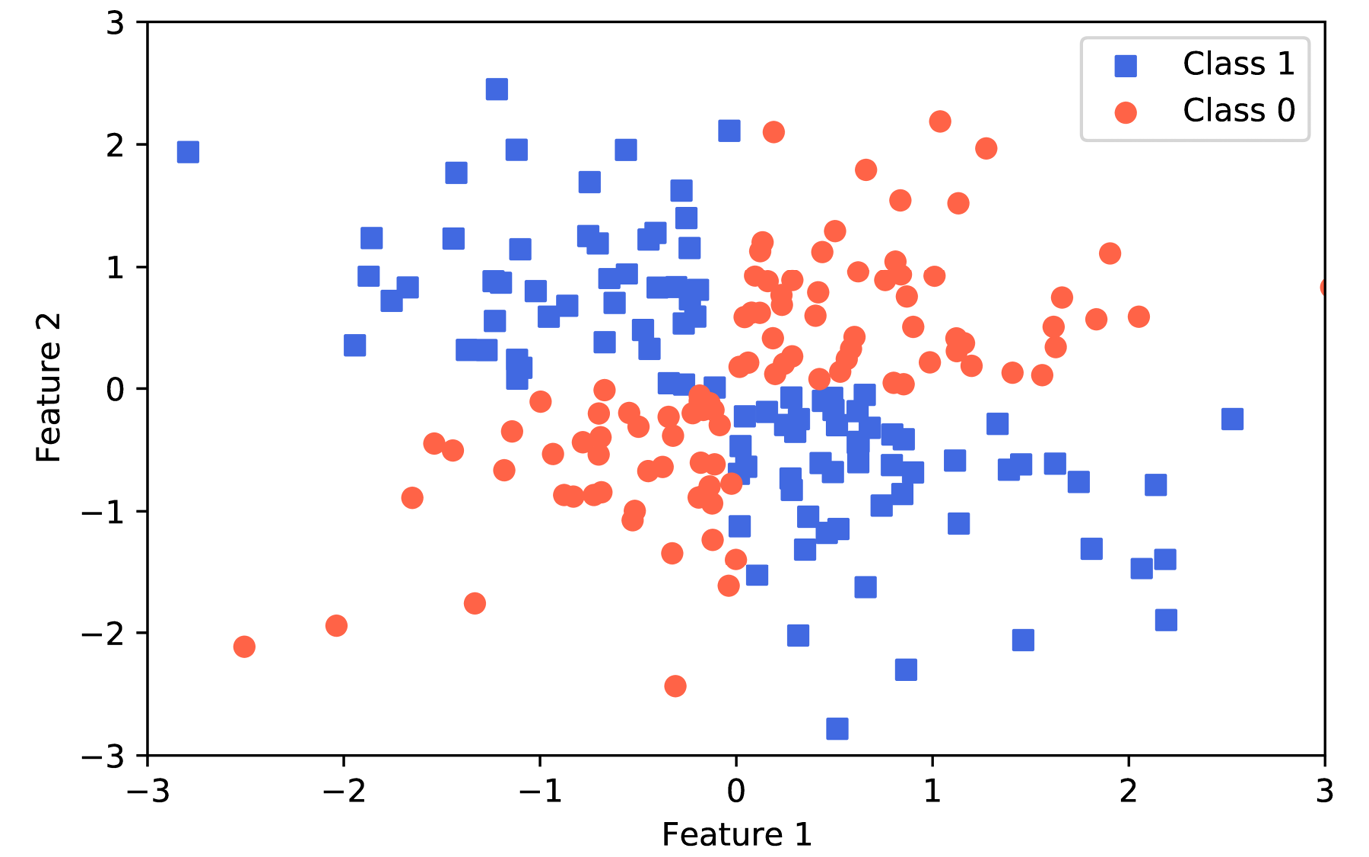
图3.13: 与或数据集绘图

很明显，我们无法通过之前小节中讨论的线性逻辑回归或线性SVM模型使用线性超平面作为决策边界去分隔正类和负类。

核方法处理这种线性不可分割数据的基本思想是创建原始特征的非线性组合来通过映射函数$\varphi$投射到更高维度的空间，在其中数据变得线性可分割。如图3.14所示，我们可以将二维数据集转换成一个新的三维特征空间，其中的类经如下的投身变得可分割：

$$\varphi (x_1,x_2)=(z_1,z_2,z_3)=(x_1,x_2,x_1^2,x_2^2)$$

这使用得我们可以通过线性超平面分割这两类，如果将该超平面投射回原特征空间，会得到一个如下图同心圈数据集所绘制的非线性决策边界：

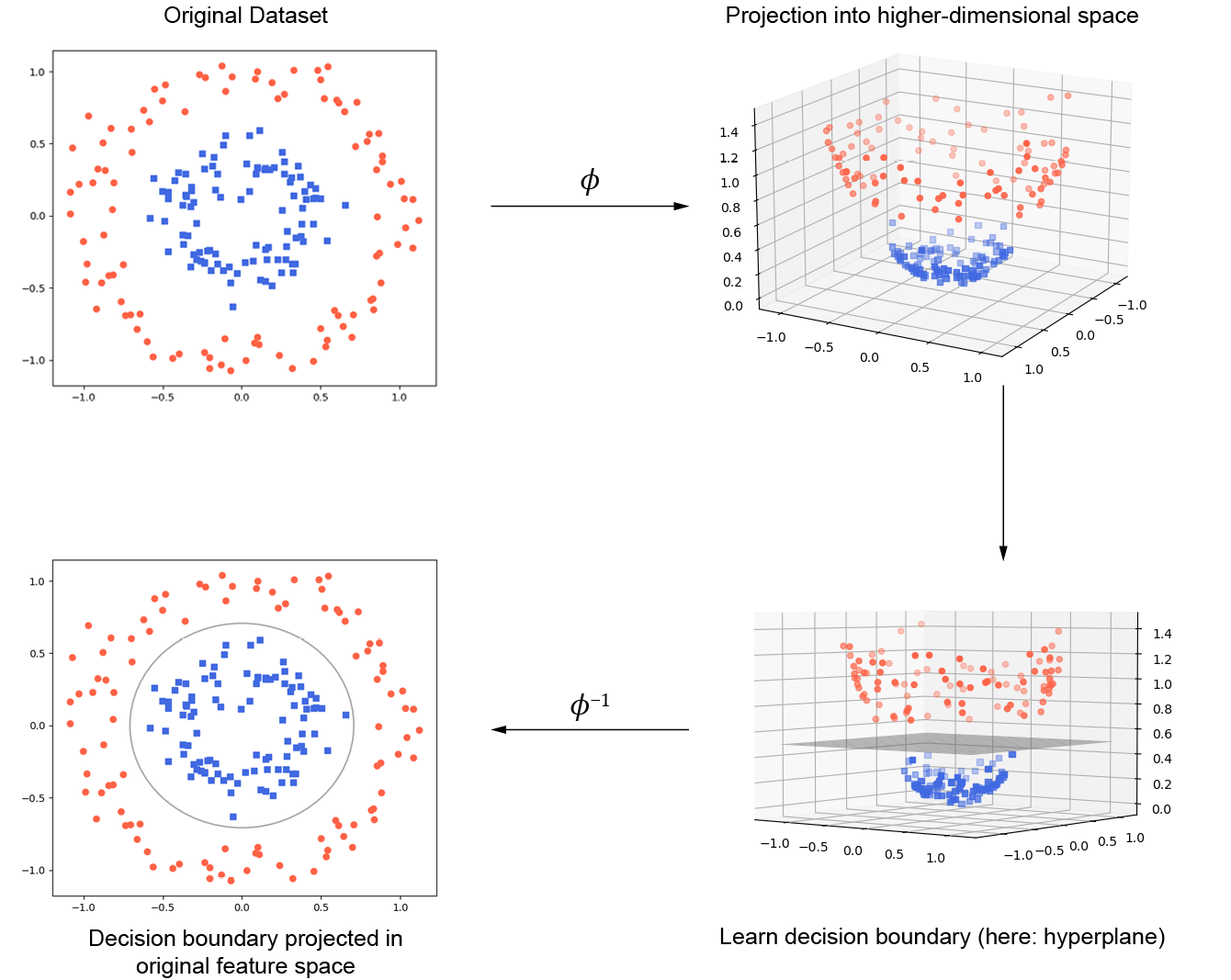
图3.4：使用核方法分类非线性数据的流程

使用核技巧在高维度平台中寻找分割超平面

要使用SVM解决非线性问题，我们会通过映射函数$\varphi$将训练数据转换成更高维度的特征空间，并训练一个线性SVM模型来对新特征空间中的数据分类。然后我们可以使用同一个映射函数$\varphi$来转换新的未知数据，使用线性SVM模型对其分类。

但这种映射方法有一个问题，就是构建新特征计算开销大，处理高维度数据时尤其如此。所以就出现了所谓的核技巧（kernel trick）。

我们没有深入讲如何解二次规划（quadratic programming）任务来训练SVM，在实操时，我们只需要通过$\varphi (x^{(i)}{)}^T\varphi (x^{(j)})$替换点乘x(i)Tx(j) 。为省去显式计算两点间点乘的大开销步骤，我们定义了核函数：

$$\mathcal{K}(x^{(i)},x^{(j)})=\varphi (x^{(i)}{)}^T\varphi (x^{(j)})$$

最广泛使用的核函数之一是径向基函数（radial basis function (RBF)）核，可以简单地称为高斯核（Gaussian kernel）：

$$\mathcal{K}(x^{(i)},x^{(j)})=\exp (-\frac{\Vert x^{(i)}-x^{(j)}{\Vert }^2}{2{\sigma }^2})$$

常简化为：

$$\mathcal{K}(x^{(i)},x^{(j)})=\exp (-\gamma \Vert x^{(i)}-x^{(j){\Vert }^2})$$

这里的$\gamma =\frac{1}{2{\sigma }^2}$是一个可优化的自由参数。

精略地说，可将“核”看成是样本对间的相似度函数，负号将距离度量反转为相似度得分，而由于指数项的原因，得到的相似度分数会在1（完全相似的样本）和0（极其不相似的样本）之间。

我们讲解了核技巧背后的全局，下面来看是否能训练出绘制很好地分割异或数据的非线性决策边界。这里我们使用了之前导入的scikit-learn的SVC类并将参数kernel='linear替换为kernel='rbf'：

>>> svm = SVC(kernel='rbf', random_state=1, gamma=0.10, C=10.0)
>>> svm.fit(X_xor, y_xor)
>>> plot_decision_regions(X_xor, y_xor, classifier=svm)
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6

从结果图可以看出，核SVM相对较好地分割了异或数据：

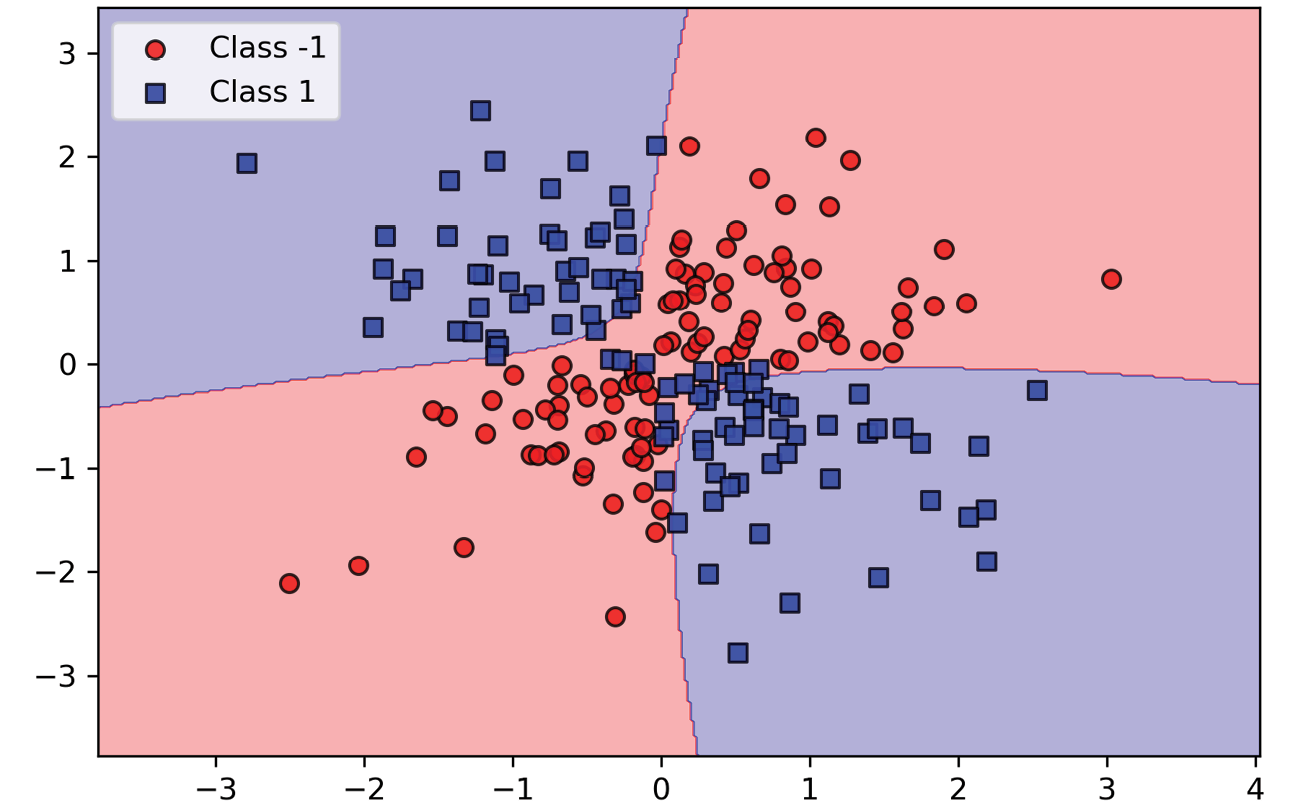
图3.15：使用核方法得到的异或数据决策边界

参数$\gamma$，我们设置为了gamma=0.1，可以理解为高斯球的临界参数。如果我们增加$\gamma$的值，就会增加训练样本的影响或范围，这会产生更紧密、更不平滑的决策边界。为更好理解$\gamma$，我们来对鸢尾花数据集应用RBF核SVM：

>>> svm = SVC(kernel='rbf', random_state=1, gamma=0.2, C=1.0)
>>> svm.fit(X_train_std, y_train)
>>> plot_decision_regions(X_combined_std,
...                       y_combined, classifier=svm,
...                       test_idx=range(105, 150))
>>> plt.xlabel('Petal length [standardized]')
>>> plt.ylabel('Petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6
7
8
9
10

因为我们为$\gamma$选择了一个相对较小的值，产生的径向基函数核SVM模型的决策边界相对柔和，如图3.16如示：

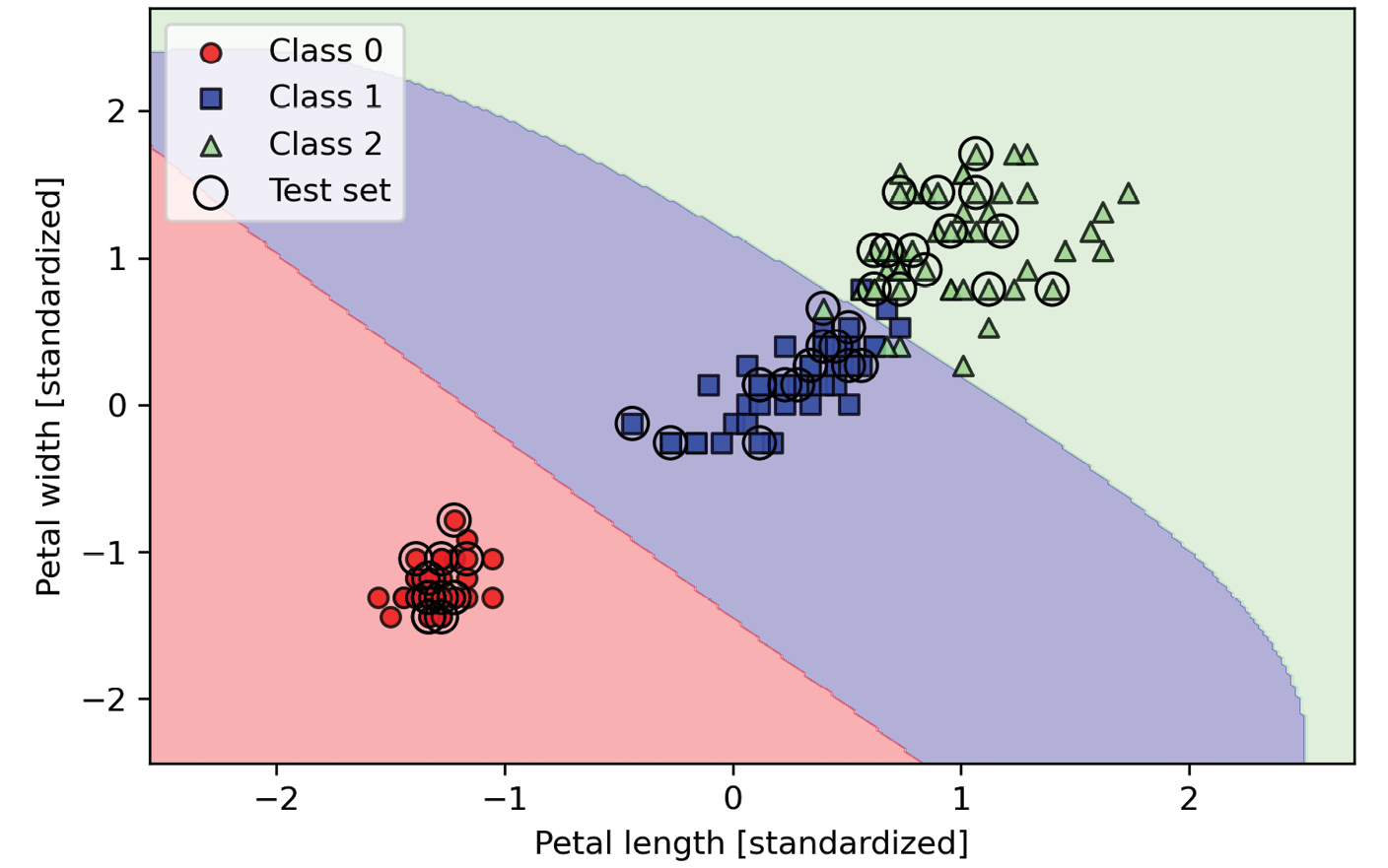
图3.16：使用小值$\gamma$的RBF核SVM模型训练鸢尾花数据集决策边界

现在我们增大$\gamma$的值并观察决策边界的效果：

>>> svm = SVC(kernel='rbf', random_state=1, gamma=100.0, C=1.0)
>>> svm.fit(X_train_std, y_train)
>>> plot_decision_regions(X_combined_std,
...                       y_combined, classifier=svm,
...                       test_idx=range(105,150))
>>> plt.xlabel('Petal length [standardized]')
>>> plt.ylabel('Petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6
7
8
9
10

在图3.17中，可以看到使用相对较大的对类0和1的$\gamma$值决策边界会变得更紧密：

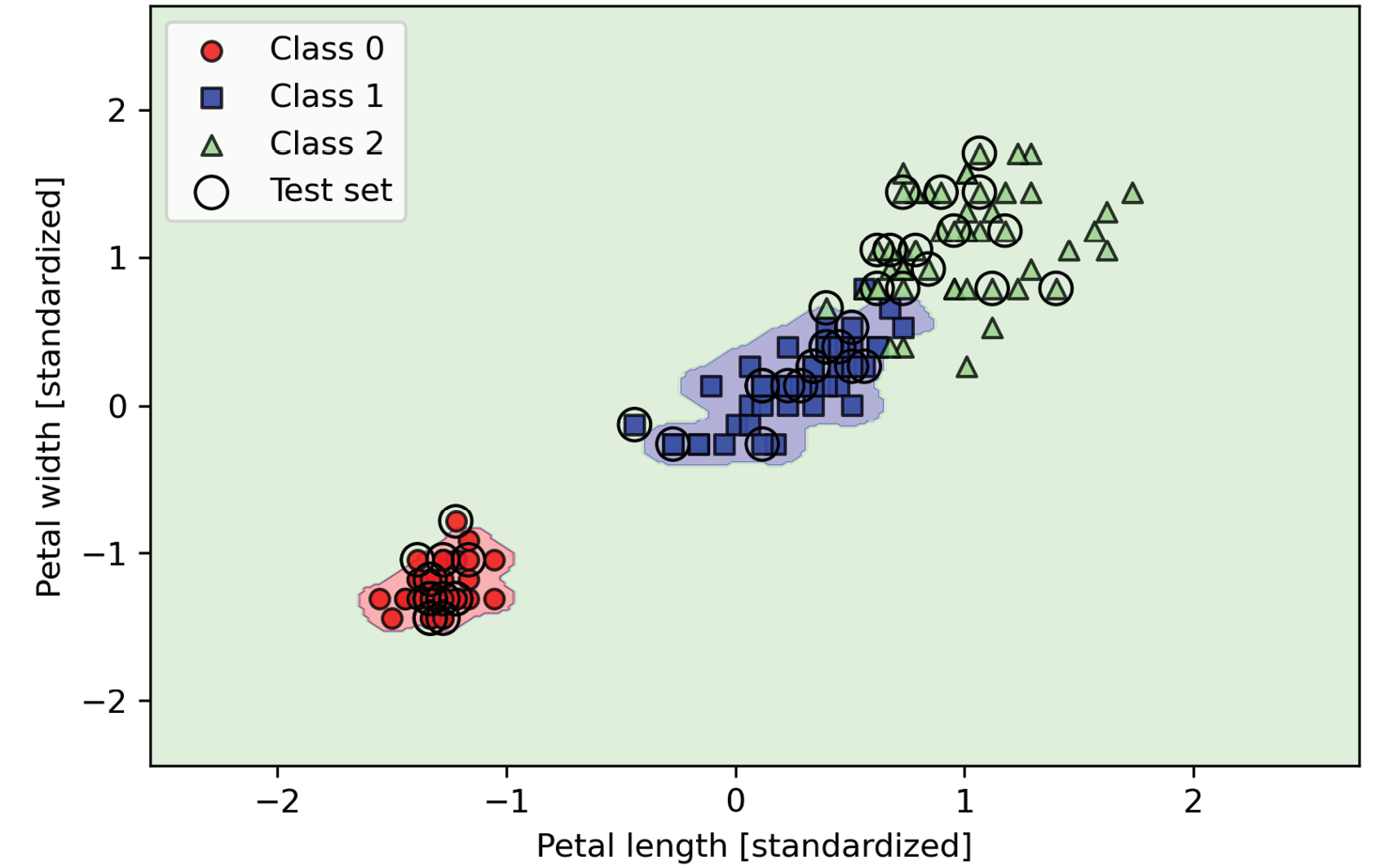
图3.17：使用大值$\gamma$的RBF核SVM模型训练鸢尾花数据集决策边界

虽然模型对训练数据集的拟合非常好，这一分类很有可能会对未知数据产生很高的泛化错误。这说明参数$\gamma$对于控制算法对训练集波动过于敏感时的过拟合或是方差扮演着重要的角色。

决策树学习

如果关注解释性决策树（decision tree**）** 分类器就是非常有吸引力的模型。 通过名称“决策树”，我们就能想到这个模型是分解数据并根据询问一系列问题做出决策。

我们通过下面使用决策树来决定某一天活动的示例来进行思考：

例3.18：决策树示例

根据训练数据集中的特征，决策树模型学习了一系列问题来推导样本的类标签。虽然图3.18基于分类变量描绘决策树的概念，同样的概念也适用于实数，比如鸢尾花数据集。例如，我们可以延花萼宽度特征轴定义一个临界值，并询问一个是非问题：“花萼宽度≥ 2.8 cm吗？”

使用这一决策算法，我们从树根节点开始，并按特征的最大信息增益（information gain (IG)）分割数据，我们会在下一节中详细讲解信息增益。在迭代处理中，我们可以对每个子节点重复这一分割步骤直接到达纯叶子节点。这就意味着每个节点上的训练样本都属于同一类。在实践中，会产生有很多节点很深的树，这很容易产生过拟合。因此，我们通常需要通常会通过设置树的最大深度来修剪树。

最大信息增益-物尽其胳膊

要按最多信息特征分割节点，我们需要定义一个目标函数来通过树学习算法进行优化。这里我们的目标函数是在每个分割点最大化信息增益，定义如下：

这里的f 是执行分割的特征，Dp和Dj是父级和第j个子点的数据集，I是杂度（impurity），Np是父节点的训练样本总数，Nj是第j个子节点的样本数。可以看出，信息增益是父节点的杂度和子节点杂度总和之间的差值：子节点杂度越低，信息增益越大。但为减化及降低组合搜索空间，大部分库（包括scikit-learn）实现的是二元决策树。这表示每个父节点分割成两个子节点，Dleft和Dright：

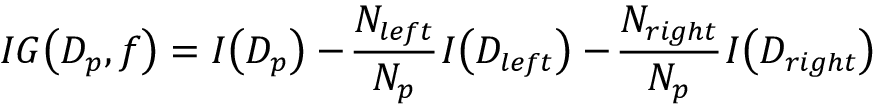
二元决策树中常用的三种杂度度量或分割标准是基尼系数（Gini impurity (IG)）、熵（entropy (IH)）和分类误差（classification error (IE)）。我们先从非空类($p(i|t)\ne 0$)熵的定义开始：

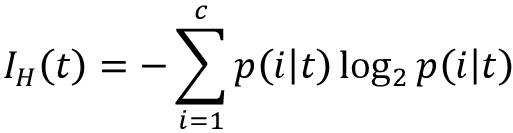
这里的p(i|t)是具体节点t属于类i的样本比率。如果节点上所有样本都属于同一类则熵为0，而在均匀类分布时熵为最大值。例如，在二元类场景中，如果p(i=1|t) = 1或p(i=0|t) = 0则熵为0。如果类均匀分布，即p(i=1|t) = 0.5且p(i=0|t) = 0.5，则熵为1。因此，如可以说熵准则（entropy criterion）试图最大化树中的互信息（mutual information）。

为在视觉上体现，我们通过如下代码可视化不同类分布的熵值：

>>> def entropy(p):
...     return - p * np.log2(p) - (1 - p) * np.log2((1 - p))
>>> x = np.arange(0.0, 1.0, 0.01)
>>> ent = [entropy(p) if p != 0 else None for p in x]
>>> plt.ylabel('Entropy')
>>> plt.xlabel('Class-membership probability p(i=1)')
>>> plt.plot(x, ent)
>>> plt.show()
1
2
3
4
5
6
7
8

下面的图3.19展示了以上代码所生成的图：

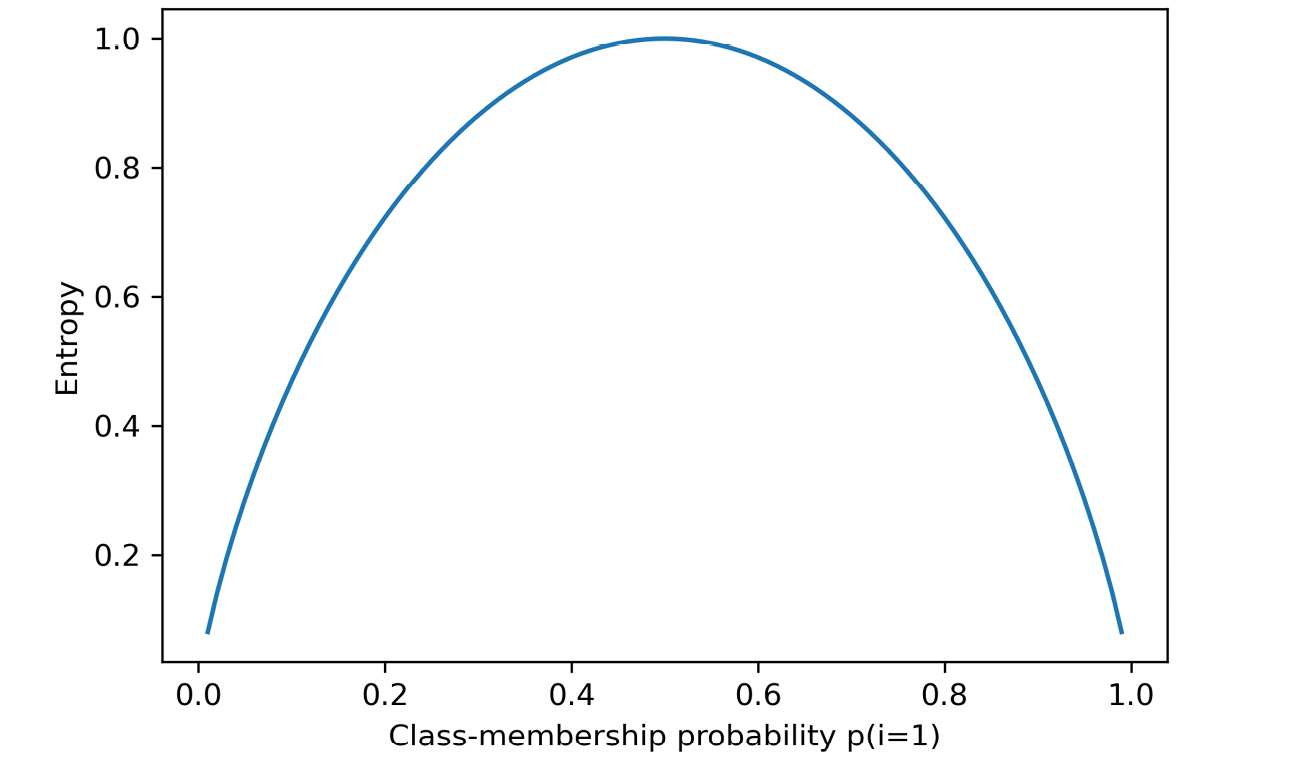
图3.19：不同类成员概率的熵值

基尼系数可以理解为最小化误分类概率的标准：

类似于熵，如果类完美混合的话基尼系数最大，例如在二元类场景(c = 2)中：

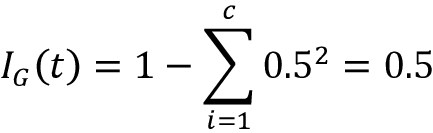
但是，在实践中，基尼系数和熵通常会产生相似的结果，一般不值得花大量时间使用不同的杂度标准而不是试验不同修剪边界来评估树。事实上，我们稍后会在图3.21中会看到，基尼系数和熵形状相似。

另一种杂度的度量是分类误差：

这是一种有用的修剪标准，但不推荐用于增长决策树，因为它对节点类概率中的变化敏感度更低。我们可以通过图3.20中的两种分割场景来进行描绘：

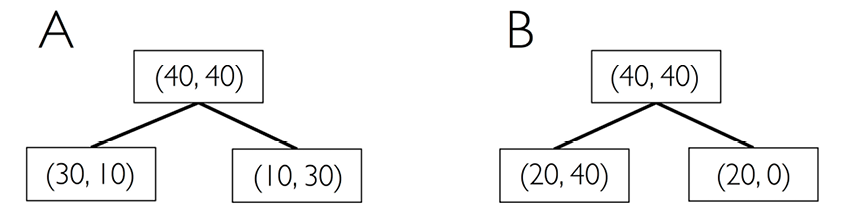
图3.20：决策树数据分割

我们从你节点中的数据集Dp开始，包含类1的40个样本和类2的40个样本，我们分割成两个数据集， Dleft和Drigh。两种场景A和B中使用分类误差作为分割标准的信息增益相同（IGE = 0.25）：

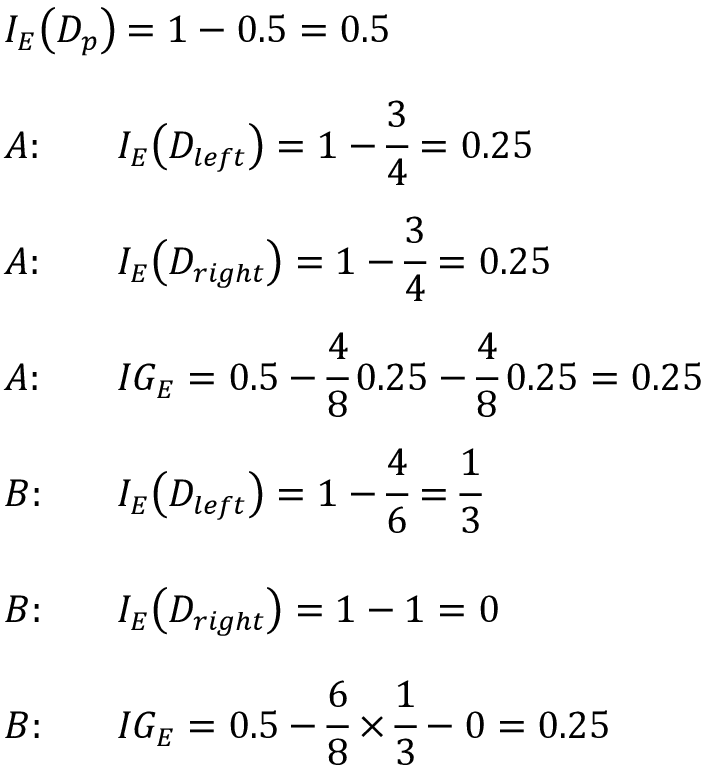
但是，基尼系数对场景B($I{G}_G=0.1\overline{6}$) 中的分类比场景A(IGG = 0.125) 要更优，纯度更高：

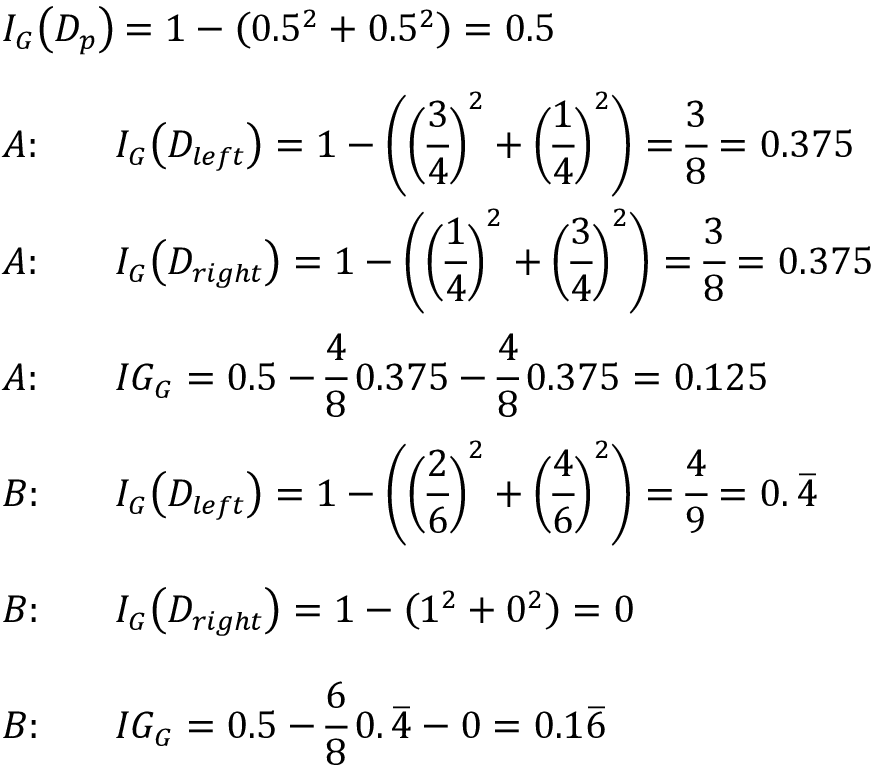
类似地，熵标准对场景B (IGH = 0.31)要优于场景(IGH = 0.19)：

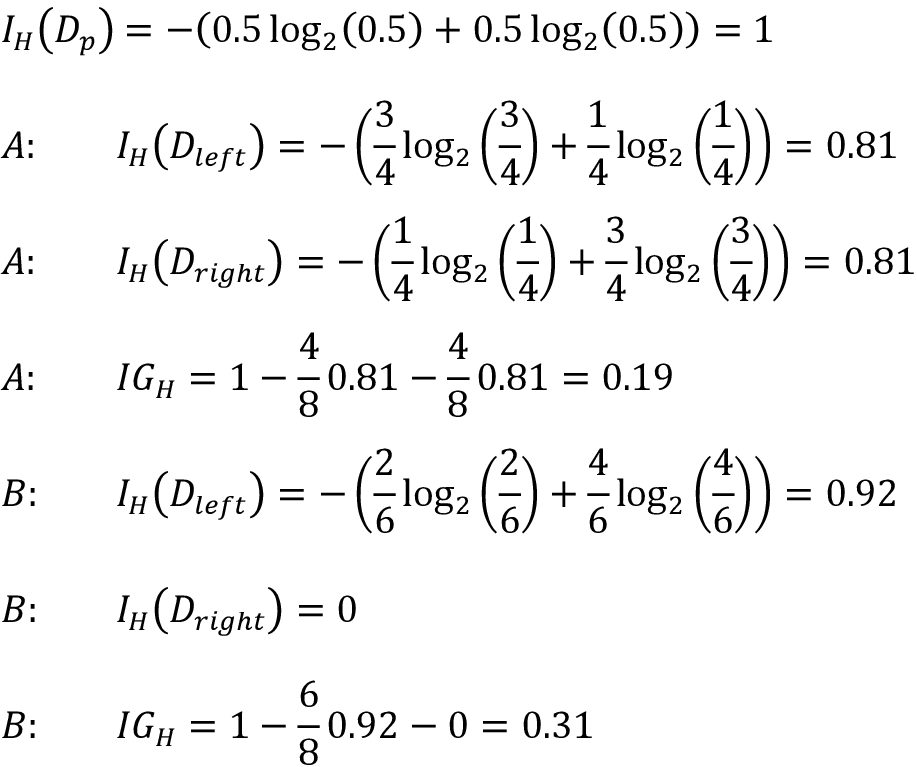
对此前讨论的三种不同的杂度标准进行可视化对比，我们为类1绘制[0, 1]概率范围内的杂度指数。我们还会添加一个缩放版本的熵(熵 / 2)来观察基尼系数是熵和分类误差间的中间度量。代码如下：

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> def gini(p):
...     return p*(1 - p) + (1 - p)*(1 - (1-p))
>>> def entropy(p):
...     return - p*np.log2(p) - (1 - p)*np.log2((1 - p))
>>> def error(p):
...     return 1 - np.max([p, 1 - p])
>>> x = np.arange(0.0, 1.0, 0.01)
>>> ent = [entropy(p) if p != 0 else None for p in x]
>>> sc_ent = [e*0.5 if e else None for e in ent]
>>> err = [error(i) for i in x]
>>> fig = plt.figure()
>>> ax = plt.subplot(111)
>>> for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err],
...                           ['Entropy', 'Entropy (scaled)',
...                            'Gini impurity',
...                            'Misclassification error'],
...                           ['-', '-', '--', '-.'],
...                           ['black', 'lightgray',
...                            'red', 'green', 'cyan']):
...     line = ax.plot(x, i, label=lab,
...                   linestyle=ls, lw=2, color=c)
>>> ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15),
...           ncol=5, fancybox=True, shadow=False)
>>> ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')
>>> ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')
>>> plt.ylim([0, 1.1])
>>> plt.xlabel('p(i=1)')
>>> plt.ylabel('impurity index')
>>> plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

上面代码生成的图如下：

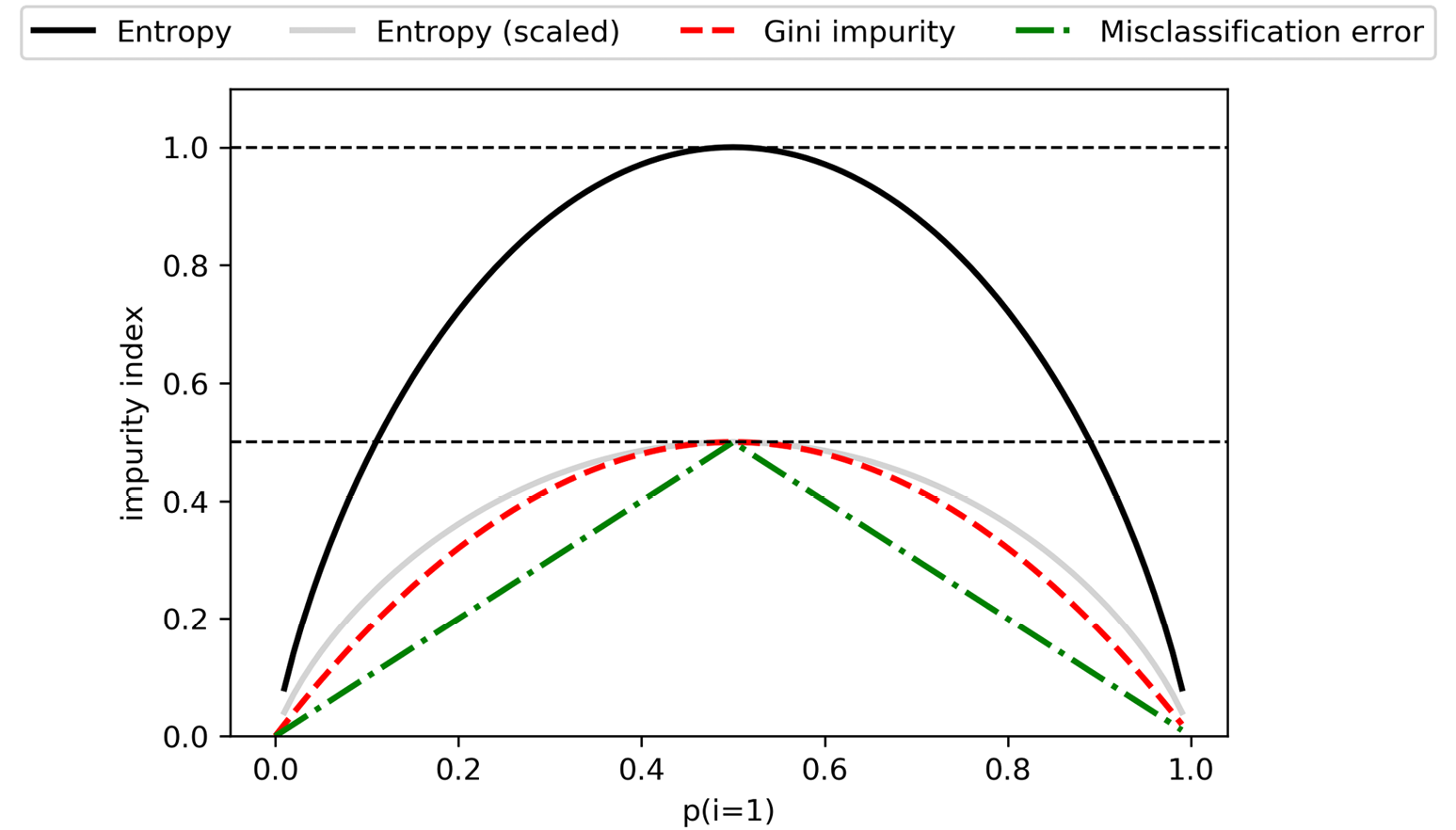
图3.21：0和1之间各类员概率的不同杂度索引

构造决策树

决策树可通过将特征空间分成矩形框构造复杂的决策边界。但我们需要小心，因为决策树越深，决策边界就越复杂，会很容易导致过拟合。现在我们使用scikit-learn训练一个最大尝试为4的决策树，以基尼系数作为杂度的标准。

虽然出于视图化考量会希望进行特征缩放，但注意特征缩放不是决策树算法的要求。代码如下：

>>> from sklearn.tree import DecisionTreeClassifier
>>> tree_model = DecisionTreeClassifier(criterion='gini',
...                                     max_depth=4,
...                                     random_state=1)
>>> tree_model.fit(X_train, y_train)
>>> X_combined = np.vstack((X_train, X_test))
>>> y_combined = np.hstack((y_train, y_test))
>>> plot_decision_regions(X_combined,
...                       y_combined,
...                       classifier=tree_model,
...                       test_idx=range(105, 150))
>>> plt.xlabel('Petal length [cm]')
>>> plt.ylabel('Petal width [cm]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在执行示例代码后，会得到决策树的平行轴决策边界：

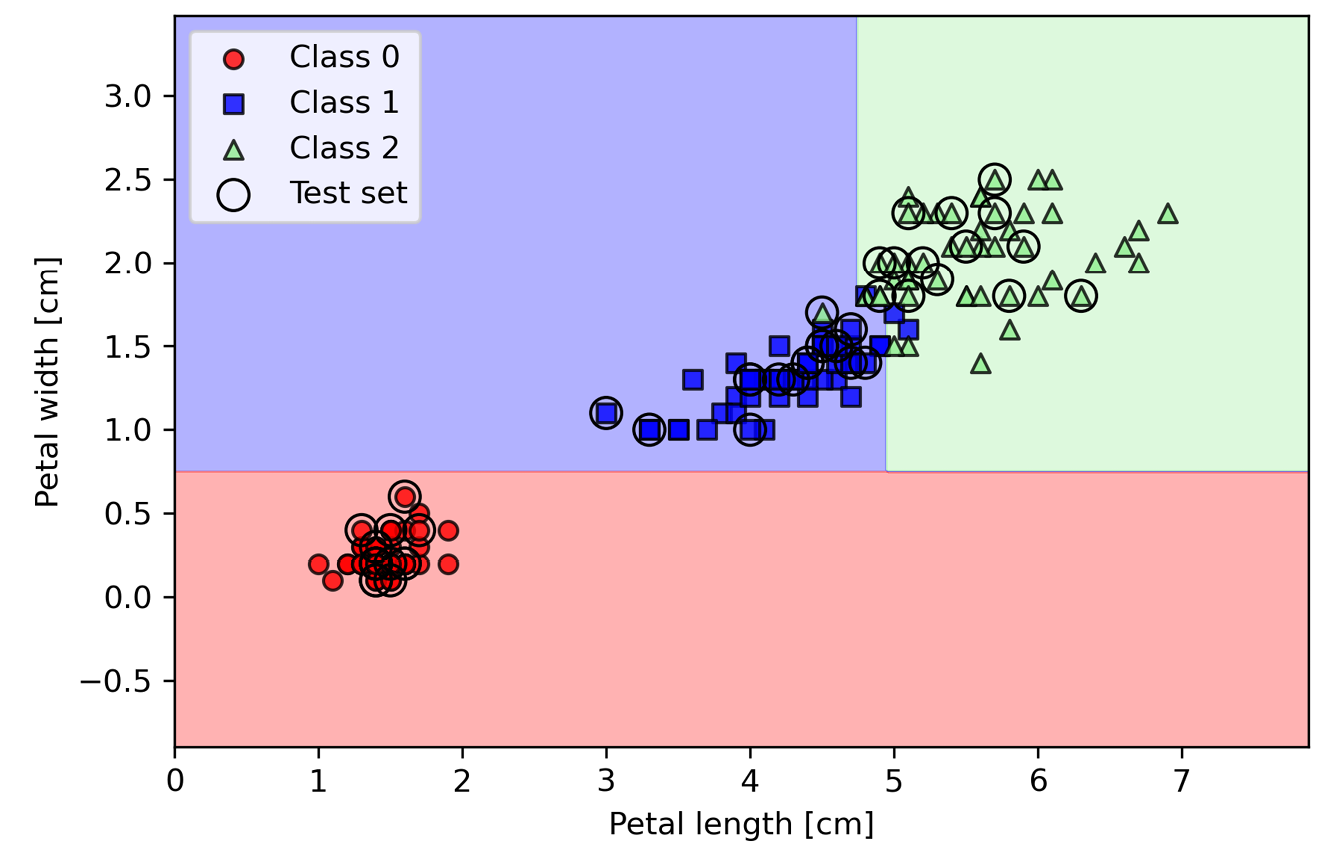
图3.22：使用决策树的鸢尾花数据决策边界

scikit-learn有一个很好的特性，那就是在通过如下代码训练后可以可视化决策树模型就了：

>>> from sklearn import tree
>>> feature_names = ['Sepal length', 'Sepal width',
...                  'Petal length', 'Petal width']
>>> tree.plot_tree(tree_model,
...                feature_names=feature_names,
...                filled=True)
>>> plt.show()
1
2
3
4
5
6
7

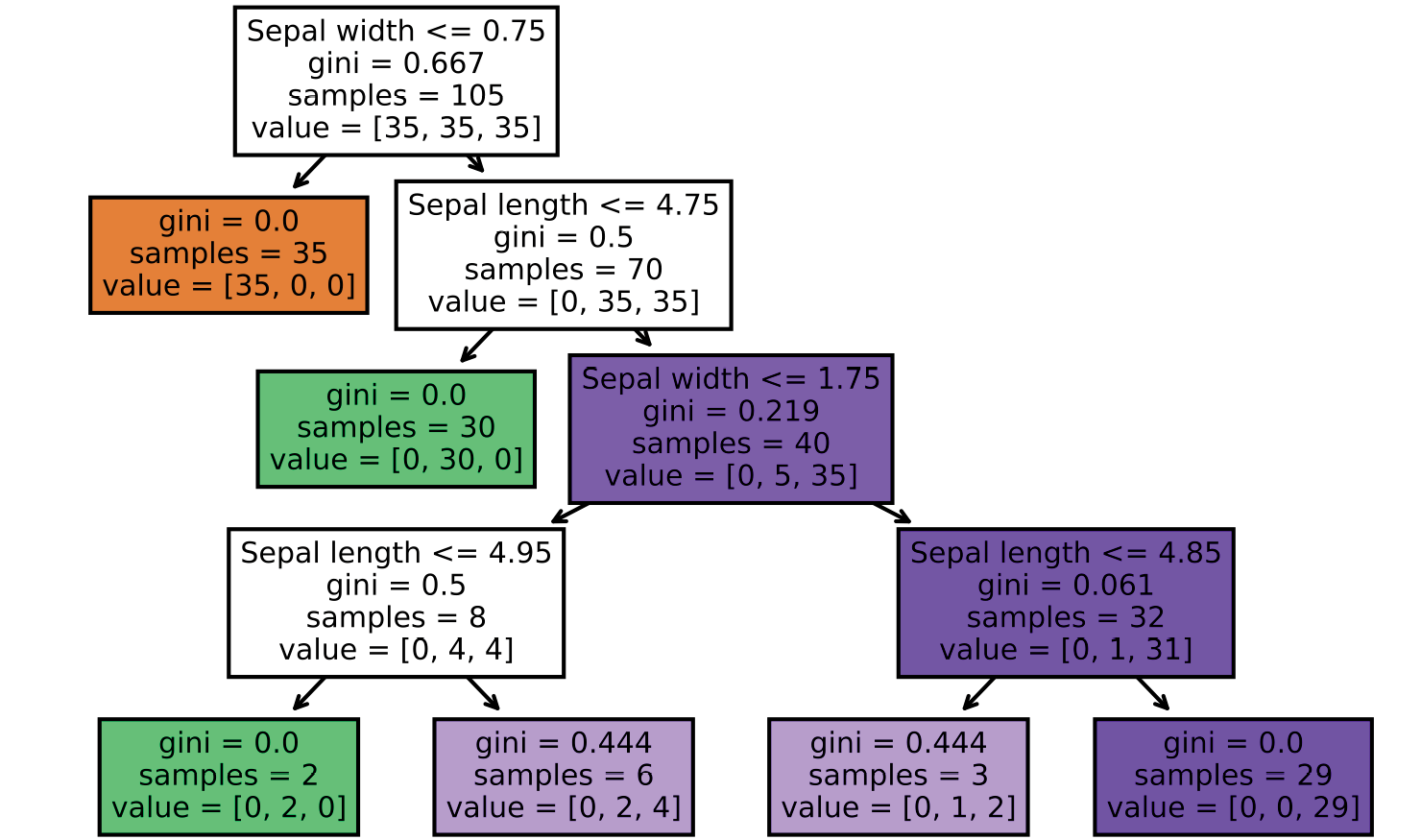
图3.23：拟合鸢尾花数据集的决策树模型

在所调用的函数plot_tree中设置了filled=True来对节点按多数类标签进行着色。还有很多其它选项，可参见官方文档：https://scikit-learn.org/stable/modules/generated/sklearn.tree.plot_tree.html。

看决策树图，我们可以很好的回溯通过训练数据集决定的决策树分割方式。对于每个节点的特征分割标准，左分支对应的是True而右分支对应的是False。

顶部的根节点开始时是105个样本。第一次分割使用花萼宽度边界≤ 0.75 cm来将根分成两个子节点，分别是35个样本（左子节点）和70个样本（右子节点）。在第一次分割后，可以看到左子节点已经很纯（基尼系数= 0），仅包含Iris-setosa类的样本。然后右子节点更进一步的分割用于将样本分成Iris-versicolor和Iris-virginica类。

查看这树及其决策区域图，可以看到决策树对花进行了很好的分类。可惜scikit-learn当前未实现手动对决策树后剪枝的功能。但我们可以回到前面的代码示例，将决策树的max_depth修改为3，与当前模型进行比较，这一练习留给感兴趣的读者。

此外，scikit-learn提供了一种自动化损失复杂度后剪枝程序。感兴趣的读者可以在下面的教程中找到更高阶的讲解：https://scikit-learn.org/stable/auto_examples/tree/plot_cost_complexity_pruning.html。

通过随机森林组合多个决策树

集成方法在过去的十年因良好的分类表现及对过拟合的健壮性在机器学习应用中获得了巨大的知名度。虽然我们会在第7章 组合不同的模型进行集成学习中讨论各种集成方法，包括装袋法（bagging）和提升方法（boosting），但这里我们讨论基于随机森林算法的决策树，众所周知它具有良好的扩展性及易用性。随机树可以看成是决策树的组合。随机森林背后的思想是平均多个（深）决策树会在构建具有更好泛化性能及更不易过拟合的更健壮模型遭受高方差的问题。随机森林可总结为4个简单步骤：

1. 画一个尺寸为n的随机引导样本（随机从训练集中选取n个有放回的样本）。

2. 通过引导样本建立决策树。在每个节点：

   1. 随机选择无放回特征d。
   2. 使用按目标函数最佳分割的特征分割节点，例如，最大化信息增益。

3. 重复步骤1-2 k次

4. 逐树累加预测按多数票分配类标签。多数票会在第7章 中讨论。

应当注意在训练单个决策树时对步骤2要做一个微调：将评估所有特征来决定最佳分割换成仅考虑其中的随机子集。

有放回和无放回抽样

以妨读者不熟悉采样的“有”和“无”放回，我们来做一个简单的实验。假设我们玩一个彩票游戏，随机抽取数字。一开始抽奖盒中有5个数字，0, 1, 2, 3和4，每次抽取一个数字。第一轮抽取到某个数字的机率是1/5。在无放回抽样中，每一轮抽完后不会将抽取的数字再放回抽奖盒。因此，下一轮抽取剩余的某个数字的概率取决于些前的轮次。例如，如果剩下的数字是0, 1, 2和4，下一轮抽到数字9的机率就是1/4。

但在有放回的随机采样中，我们总是会将抽取到的数字放回抽奖盒，因此抽取到某个数字的概率保持不变，同一个数字可以抽到多次。换句话说，在有放回抽样中，样本（数字）是独立的，协方差为0。例如，随机抽取5轮数字后的结果会是这样：

• 无放回随机采样：2, 1, 3, 4, 0
• 有放回随机采样：1, 3, 3, 4, 1

虽然随机森林没有提供和决策树相同级别的可解释性，随机森林的一个巨大优势是不太需要担心超参数值的选择。通常不需要对随机森林进行修剪，因为集成模型对于各决策树中预测平均值的噪声非常健壮。在实操时我们需要注意的唯一参数是从随机森林中选择的树的数量 k（第3步）。通常树的数量越大，随机森林分类器在计算开销增加的情况下表现也越好。

虽然在实操中很少见，随机森林分类器的其它可分别优化（使用第6章 学习模型评估和超参数调优的最佳实践中的技术）的超参数有：引导样本（第1步）的大小n，每次分割随机选择的特征数d（第2a步）。通过引导样本的样本大小n，我们可以控制随机森林的偏差-方差均衡。

减小引导样本的大小会增加各树间的多样性，因为引导样本中包含具体训练样本的概率变小了。因此，收缩引导样本的大小通常会增加随机森林的随机性，有助于减小过拟合的效果。但更小的引导样本通常会导致更低的随机森林全局表现以及训练和测试表现的小间隙，但整体测试表现更低。相反，增加引导样本的大小会增加过拟合的程度。因为引导样本，进而各决策树，彼此会变得更相近，它们会学习更紧密地拟合原训练数据集。

在大部分实现中，包含scikit-learn中的RandomForestClassifier实现，选择的引导样本的大小与原训练数据集中的训练样本数相同，通常可达到良好的偏差-方差均衡。对于每次分割的特征数d，我们希望选择一个小于训练集中总特征数的值。scikit-learn中使用了合理的默认值，其它实现则为$d=\sqrt{m}$，其中的m为训练数据集中的特征数。

我们不用自己通过各决策树构建随机森林分类器，在scikit-learn已经为了实现了可供使用的实现：

>>> from sklearn.ensemble import RandomForestClassifier
>>> forest = RandomForestClassifier(n_estimators=25,
...                                 random_state=1,
...                                 n_jobs=2)
>>> forest.fit(X_train, y_train)
>>> plot_decision_regions(X_combined, y_combined,
...                       classifier=forest, test_idx=range(105,150))
>>> plt.xlabel('Petal length [cm]')
>>> plt.ylabel('Petal width [cm]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

执行以上代码，应该会看到由随机森林中树的组合所形成的决策区域，如图3.24所示：

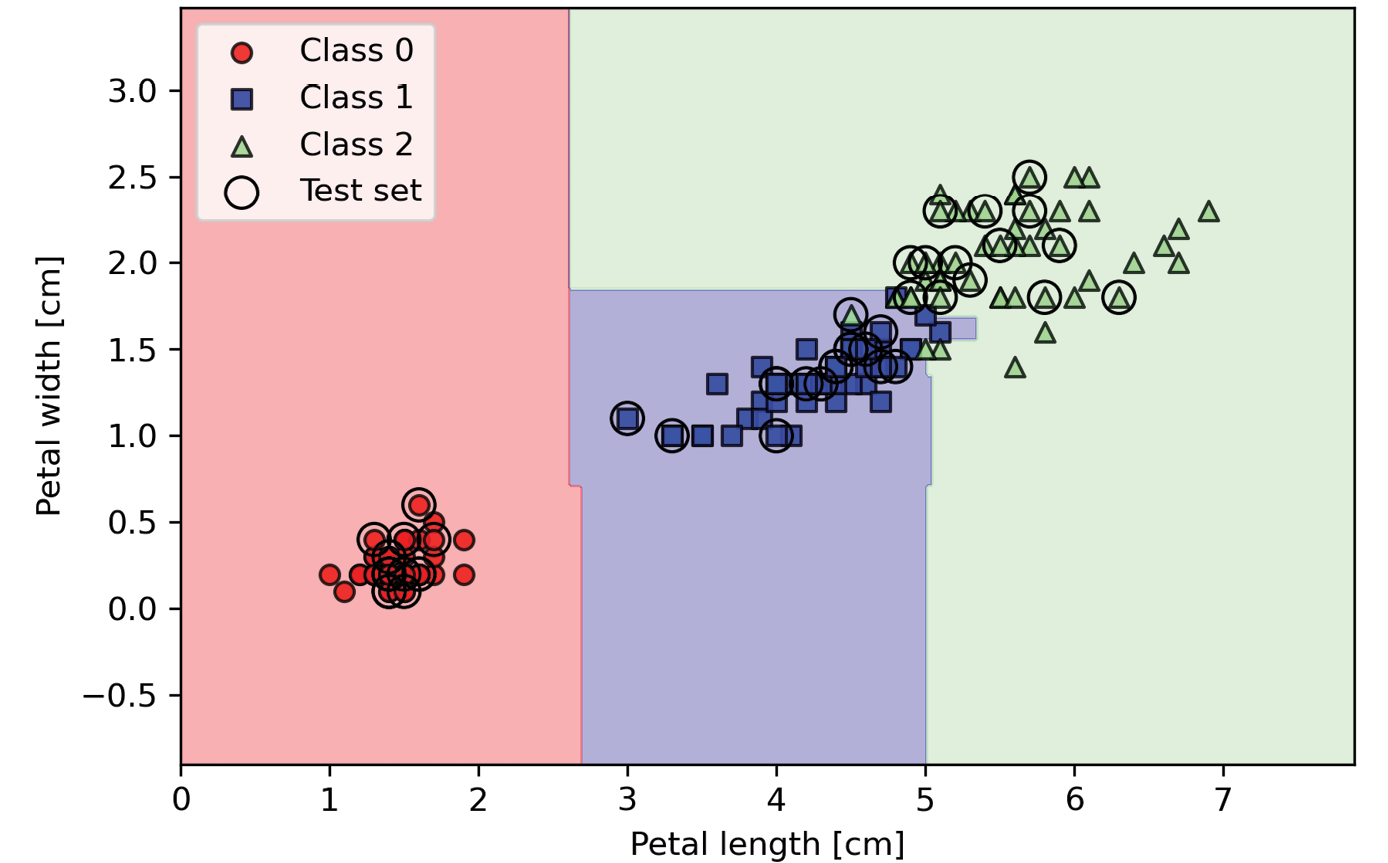
图3.24：使用随机森林训练的鸢尾花数据集的决策边界

使用上面的代码，我们通过n_estimators参数设置的25个决策树的训练了一个随机森林。默认，它使用基尼系数度量作为分割节点的标准。我们通过很小的训练数据集生成一个很小的随机森林，出于演示目的使用了n_jobs参数，这让我们可以使用计算机的多核（这里为双核）来并行训练模型。如果这段代码出现错误，说明你的电脑可能不支持多进程。那么可以省去n_jobs参数或设置为n_jobs=None。

K最近邻-一种惰性学习算法

本章我们最后要讨论的监督学习算法是K最近邻(KNN)分类器，它非常有意思，因为它与我们至此所讨论其它学习算法都有根本性的不同。

KNN是惰性学习的典型。称之为“惰性”不是因其明显的简单性，而是因为它不是从训练集学习一个判别函数，却去记住训练数据集。

参数化和非参数化模型

机器学习算法可分成参数化和非参数化模型。使用参数化模型，我们从训练数据集评估参数学习一个可分类新数据点的函数，无需再使用原数据集。典型的参数化模型是感知机、逻辑回归和线性SVM。相反， 非参数化模型无法通过固定的参数集特征化，并且随训练数据量的变化参数数量也发生改变。到此的两种非参数化模型的的例子是决策树分类器/随机森林和核（但非线性）SVM。

KNN属于非参数化模型的子类，称为基于实例的学习。基于实例学习的模型通过记忆训练数据集来特征化，惰性学习是基于实例的学习的到处跑特殊情况，在学习过程中无（零）损失。

KNN算法本身相当直接，可总结为如下步骤：

1. 选择k 的数量以及距离指标
2. 查找希望分类的数据记录的k最近邻
3. 通过多数票分配类标签

图3.25描绘了一个新数据点( ? ) 如何根据5个最近邻中的多数票来分配三角类标签：

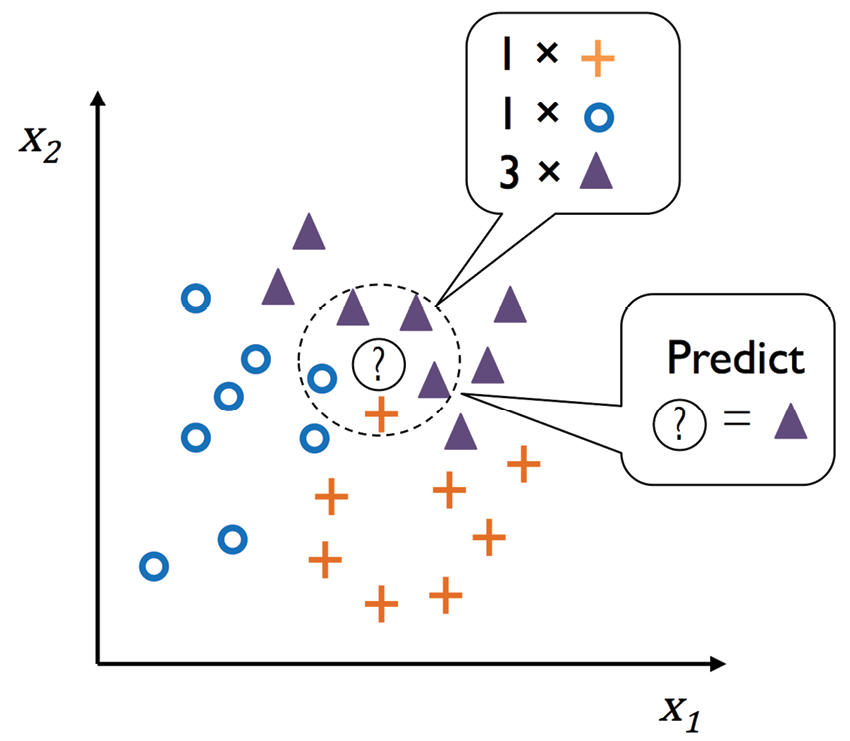
图3.25：k最近邻的实现原理

根据所选择的距离指标，KNN查找训练集中与希望分类点最近（最相似）的k个样本。然后通过k个最近邻居的多数票决定数据点的类标签

基于内存方法的优势和劣势

这种基于类型方法的主要优势是分类器可以在收集新训练数据时实时调整。但缺点是分类新样本的计算复杂度在最差场景中随训练数据集样本数的增加线性上升，除非数据维度（特征）很少并且算法使用高效数据结构实现，可高效查询训练数据。这类数据结构有k-d树(https://en.wikipedia.org/wiki/K-d_tree)和球树(https://en.wikipedia.org/wiki/Ball_tree)，在scikit-learn中对两者都提供了支持。除查询数据的计算开销外，大数据集对于有限的存储空间来说也是个问题。

但是，对于很多处理相对小到中型数据集的案例，基于内存的方法提供很好的预测和计算性能，因此对很多真实世界的问题是个好选择。使用最近邻方法近期的案例有预测制药目村的属性(Machine Learning to Identify Flexibility Signatures of Class A GPCR Inhibition, Biomolecules, 2020, Joe Bemister-Buffington, Alex J. Wolf, Sebastian Raschka和Leslie A. Kuhn, https://www.mdpi.com/2218-273X/10/3/454) 和最新的语言模型(高效最近邻语言模型 2021, Junxian He, Graham Neubig和Taylor Berg-Kirkpatrick, https://arxiv.org/abs/2109.04212)。

通过执行如下代码，我们使用欧式距离（Euclidean distance）指标实现scikit-learn中的KNN模型：

>>> from sklearn.neighbors import KNeighborsClassifier
>>> knn = KNeighborsClassifier(n_neighbors=5, p=2,
...                            metric='minkowski')
>>> knn.fit(X_train_std, y_train)
>>> plot_decision_regions(X_combined_std, y_combined,
...                       classifier=knn, test_idx=range(105,150))
>>> plt.xlabel('Petal length [standardized]')
>>> plt.ylabel('Petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()
1
2
3
4
5
6
7
8
9
10
11

通过对这一数据集指定KNN模型的五个邻居，我们获取了一个相对平滑的决策边界，如图3.26所示：

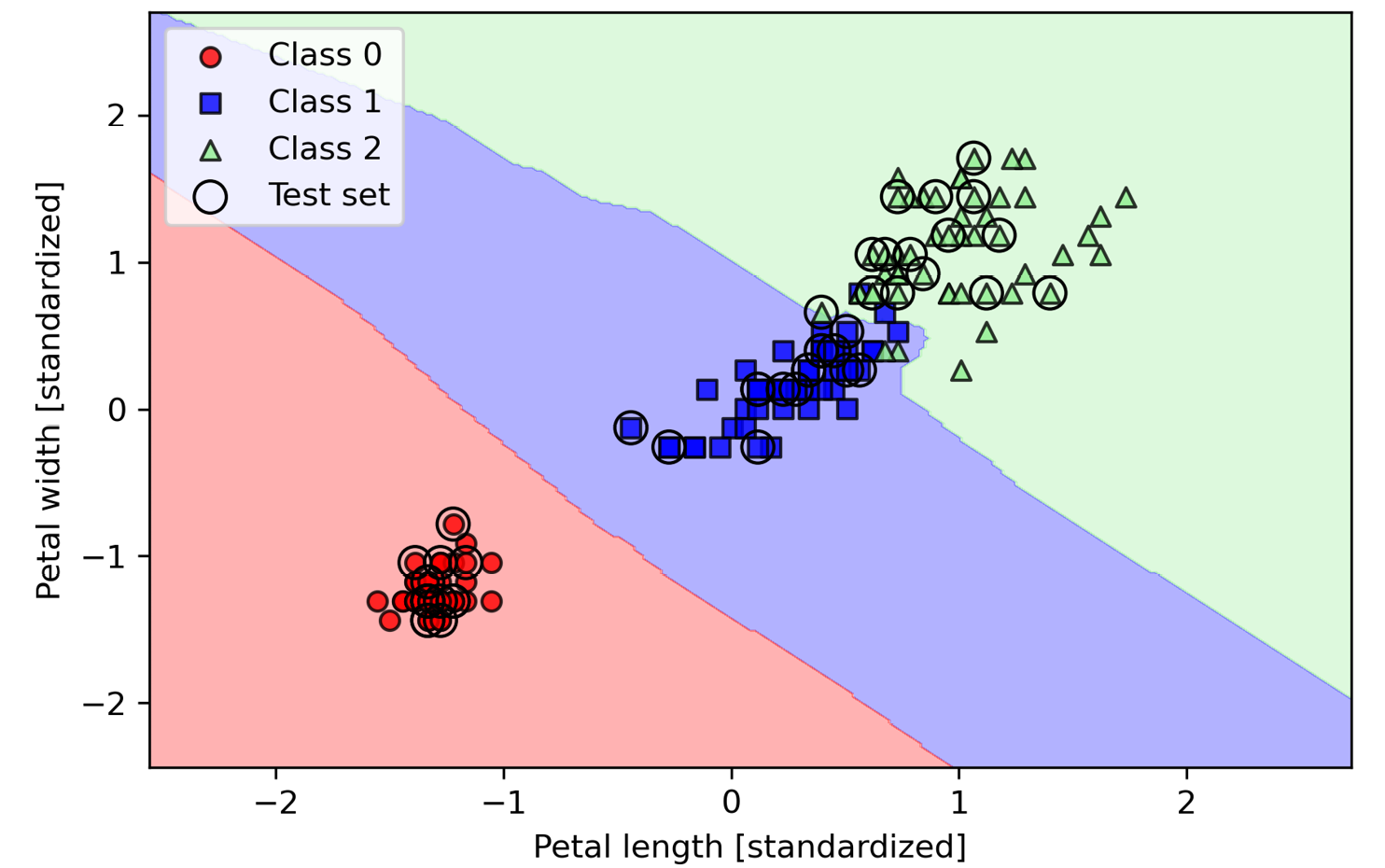
图3.26：鸢尾花数据集的k最近邻决策边界

解决平局问题

在出现平局时，scikit-learn中KNN算法的实现会选择距离待分类数据记录距离更近的邻居。如果这些邻居距离相似，算法会选择训练集中先出现的类标签。

对k的正确选择对在过拟合和欠拟合间找到平衡至关重要。我们还要确保选择适合数据集中特征的距离指标。通常，欧式距离度量用于实数值案例，比如我们鸢尾花数据集中的花，特征通过厘米度量。但如果使用欧式距离，一定要标准化数据这样每个特征对距离的贡献相同。我们在前面的代码中使用的minkowski(明可夫斯基)距离是对欧式距离和曼哈顿（Manhattan）距离的泛化，写成这样：

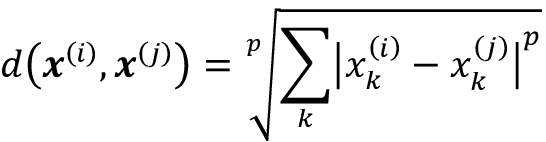
如果设置参数p=2就变成欧式距离，设置p=1就变成曼哈顿距离。scikit-learn中有很多其它距离度量，可通过metric参数指定。可在https://scikit-learn.org/stable/modules/generated/sklearn.metrics.DistanceMetric.html中查看。

最后，有必要提一下KNN很容易因维数灾难（curse of dimensionality）出现过拟合。维数灾难是一种特征空间随固定大小训练数据集维数增加而越来越稀疏的现象。我们可以把最近邻居看成高维空间更远距离来进行很好的评估。

我们在逻辑回归相关节中讨论到正则化的概念是避免过拟合的一种方式。但对于无法正则化的模型，比如决策树和KNN，我们可以使用特征选择和数据降维技术来帮助我们避免维数灾难。这会在接下来的两章中详细讨论。

使用的GPU其它机器学习实现

在处理大数据集时，运行k最近邻或通过多预估器拟合随机森林要求大量的计算资源和处理时间。如果电脑内置了兼容近期版本NVIDIA的CUDA库的NVIDIA GPU，推荐考虑RAPIDS生态(https://docs.rapids.ai/api)。比如RAPIDS的cuML(https://docs.rapids.ai/api/cuml/stable/)库实现了很多支持GPU加速的scikit-learn机器学习算法。可https://docs.rapids.ai/api/cuml/stable/estimator_intro.html上找到对cuML的简介。如果有兴趣学习RAPIDS生态，也可免费访问地本书作者与RAPIDS团队合作的期刊文章：Python机器学习: 数据科学、机器学习和人工智能的主要开发和技术趋势(https://www.mdpi.com/2078-2489/11/4/193)。

小结

本章中我们学习了很用于处理线性和非线性问题的机器学习算法。我学习了决策树，对于关心可解释性时尤具吸引力。逻辑回归不仅是基于SGD有用的在线学习模型，还可以用于预测具体事件的概率。

虽然SVM是可通过核技巧扩展至非线性问题强大的线性模型，但有很多参数需要调优才能实现良好的预测。相反， 集成方法，比如随机森林，无需很多的参数调优，不像决策树那样容易过拟合，这让其成为很多实践问题领域有吸引力的模型。KNN分类器通过惰性学习为分类提供了另一种方法，无需任何模型训练即可实现预测，但预测步骤的计算开销更大。

但比选择合适学习算法更重要的是训练集中的数据。没有有用信息和可判别特征任何算法都无法做出很好的预测。

下一章中，我们会讨论数据预处理、特征选择和数据降维相关的重要内容，这表示我们需要构建更强大的机器学习模型。稍后的第6章 学习模型评估和超参数调优的最佳实践中，我们还会学习如何评估和比较模型的性能以及调优不同算法的有用技巧。