devbox
知新_RL
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【深度学习】Softmax实现手写数字识别

作者：知新_RL | 2024-02-07 21:12:53

赞

踩

【深度学习】Softmax实现手写数字识别

实训1：Softmax实现手写数字识别

相关知识点: numpy科学计算包，如向量化操作，广播机制等

1 任务目标

1.1 简介

本次案例中，你需要用python实现Softmax回归方法，用于MNIST手写数字数据集分类任务。你需要完成前向计算loss和参数更新。

你需要首先实现Softmax函数和交叉熵损失函数的计算。
y = s o f t m a x ( W T x + b ) L = C r o s s E n t r o p y ( y , l a b e l ) y=softmax(W^Tx+b)\\ L=CrossEntropy(y,label) y=softmax(WTx+b)L=CrossEntropy(y,label)
在更新参数的过程中，你需要实现参数梯度的计算，并按照随机梯度下降法来更新参数。
∂ L ∂ W , ∂ L ∂ b \frac{\partial L}{\partial W},\frac{\partial L}{\partial b} ∂W∂L​,∂b∂L​
具体计算方法可自行推导，或参照第三章课件。

1.2 MNIST数据集

​ MNIST手写数字数据集是机器学习领域中广泛使用的图像分类数据集。它包含60,000个训练样本和10,000个测试样本。这些数字已进行尺寸规格化，并在固定尺寸的图像中居中。每个样本都是一个784×1的矩阵，是从原始的28×28灰度图像转换而来的。MNIST中的数字范围是0到9。下面显示了一些示例。 注意：在训练期间，切勿以任何形式使用有关测试样本的信息。

image.png

1.3 任务要求

  1. 代码清单

    • a) data/ 文件夹：存放MNIST数据集。你需要下载数据，解压后存放于该文件夹下。下载链接见文末，解压后的数据为 *ubyte 形式；
    • b) solver.py 这个文件中实现了训练和测试的流程。建议从这个文件开始阅读代码；
    • c) dataloader.py 实现了数据加载器，可用于准备数据以进行训练和测试；
    • d) visualize.py 实现了plot_loss_and_acc函数，该函数可用于绘制损失和准确率曲线；
    • e) optimizer.py 你需要实现带momentum的SGD优化器，可用于执行参数更新；
    • f) loss.py 你需要实现softmax_cross_entropy_loss，包含loss的计算和梯度计算；
    • g) runner.ipynb 完成所有代码后的执行文件，执行训练和测试过程。

  2. 要求

    我们提供了完整的代码框架，你只需要完成optimizer.py，loss.py 中的 #TODO部分。你需要提交整个代码文件和带有结果的runner.ipynb (不要提交数据集) 并且附一个pdf格式报告，内容包括：

    • a) 记录训练和测试的准确率。画出训练损失和准确率曲线；

    • b) 比较使用和不使用momentum结果的不同，可以从训练时间，收敛性和准确率等方面讨论差异；

    • c) 调整其他超参数，如学习率，Batchsize等，观察这些超参数如何影响分类性能。写下观察结果并将这些新结果记录在报告中。

1.4 注意事项

  1. 注意代码的执行效率，尽量不要使用for循环；
  2. 不要在pdf报告中粘贴很多代码(只能包含关键代码)，对添加的代码作出解释;
  3. 不要使用任何深度学习框架，如TensorFlow，Pytorch等；
  4. 禁止抄袭。

1.5 参考

  1. 数据集下载：http://yann.lecun.com/exdb/mnist/index.html

2 代码设计

2.1 Solver.py

这段代码实现了一个Solver类，用于实现基于Softmax模型的训练和评估，主要包括以下几个部分：

  1. 模型（SoftmaxCrossEntropyLoss）：
    • 在 __init__ 方法中，构建了一个简单的 softmax 回归模型，用于图像分类任务。
    • 通过cfg字典写入模型的配置信息。
    • 包含了权重参数 W 和偏差参数 b，通过 forward 方法实现了前向传播，计算损失和准确率。
    • 通过 gradient_computing 方法计算了权重参数 W 和偏差参数 b 的梯度。
  2. 数据加载器（Dataloader）：
    • 使用 build_loader 方法构建了训练、验证和测试的数据加载器。
    • 数据加载器通过 build_dataloader 函数从数据集中加载数据，并提供按批次获取数据的功能。
  3. 优化器（SGD）：
    • 使用 build_optimizer 方法构建了随机梯度下降（SGD）优化器。
    • 优化器通过 step 方法实现了一次权重的更新，使用了动量（momentum）来平滑参数更新。
  4. 训练循环（train）：
    • 使用 train 方法进行模型训练，包含了多个 epoch 的训练循环。
    • 在每个 epoch 中，通过遍历训练集的迭代器，进行前向传播、梯度计算和权重更新。
    • 打印每个 iteration 的训练损失和准确率，并在每个 epoch 结束后打印平均训练损失和准确率。
    • 在每个 epoch 结束后，使用 validate 方法计算验证集上的损失和准确率。
  5. 验证循环（validate）：
    • 使用 validate 方法在验证集上进行验证，计算平均损失和准确率。
  6. 测试循环（test）：
    • 使用 test 方法在测试集上进行测试，计算平均损失和准确率。

​ 这个框架提供了一个基本的训练流程，可以用于训练和评估一个简单的 softmax 回归模型。在训练过程中，使用了随机梯度下降优化器，动量用于加速参数更新。在每个 epoch 结束后，打印训练集和验证集上的平均损失和准确率。

2.2 loss.py

这段代码实现了SoftmaxCrossEntropyLoss 类，用于计算多类别分类问题中的 softmax 交叉熵损失。

  1. 初始化函数 __init__：

    • num_input：每个输入样本的大小。
    • num_output：每个输出样本的大小，即类别的数量。
    • trainable：标志是否可以训练，如果设置为 True，则表示该层的权重可以通过梯度下降等优化算法进行更新。

  2. 前向传播函数 forward：

    • 接收输入矩阵 Input 和标签 labels。

    • 计算线性变换 z = Input ⋅ W + b z = \text{Input} \cdot \text{W} + \text{b} z=Input⋅W+b。

      代码如下：

      # 计算输出矩阵
z = np.dot(Input, self.W) + self.b

      • 1
      • 2

    • 计算 Softmax 激活函数，得到概率分布 softmax_probs。

      Softmax函数的定义是：
      a i = e x i ∑ k = 1 n e x k a_i = \frac{e^{x_i}}{\sum_{k=1}^n e^{x_k}} ai​=∑k=1n​exk​exi​​
      其中， a i a_i ai​是第i个类别的预测概率， x i x_i xi​是第i个类别的网络输出，n是类别的总数。Softmax函数的特点是：

      • 它可以将任意的输入映射到(0,1)区间，表示概率。
      • 它的输出的和为1，表示概率分布。
      • 它是单调递增的，即输入越大，输出越大。
      • 它是可微的，即可以求导数。

      代码如下：

      # 计算 softmax
softmax_probs = np.exp(z) / np.sum(np.exp(z), axis=1, keepdims=True)

      • 1
      • 2

    • 计算交叉熵损失 loss，度量模型预测与实际标签之间的差异。

      交叉熵损失函数的定义是：
      L = − ∑ i = 1 n y i log ⁡ a i L = -\sum_{i=1}^n y_i \log a_i L=−i=1∑n​yi​logai​
      其中， y i y_i yi​是第i个类别的真实标签， a i a_i ai​是第i个类别的预测概率，n是类别的总数。交叉熵损失函数的特点是：

      • 它是非负的，即损失值总是大于等于0。
      • 它是凸的，即存在一个全局最小值。
      • 它是可微的，即可以求导数。
      • 它的最小值为0，当且仅当真实标签和预测概率完全相同。

      代码如下：

      # 计算交叉熵损失
batch_size = Input.shape[0]
loss = -np.sum(np.log(softmax_probs[np.arange(batch_size), labels] + EPS)) / batch_size

      • 1
      • 2
      • 3

    • 计算预测准确度 acc。

      代码如下：

      # 计算准确度
predicted_labels = np.argmax(softmax_probs, axis=1)
acc = np.mean(predicted_labels == labels)

      • 1
      • 2
      • 3

  3. 梯度计算函数 gradient_computing：

    • 接收输入矩阵 Input 和标签 labels。

    • 计算线性变换 z = Input ⋅ W + b z = \text{Input} \cdot \text{W} + \text{b} z=Input⋅W+b 和 Softmax 激活函数，得到概率分布 softmax_probs。

      代码如下：

      # 计算输出矩阵
z = np.dot(Input, self.W) + self.b

      • 1
      • 2

    • 计算 Softmax 交叉熵损失对模型输出的梯度 softmax_grad。
      a i = e x i ∑ k = 1 n e x k a_i = \frac{e^{x_i}}{\sum_{k=1}^n e^{x_k}} ai​=∑k=1n​exk​exi​​
      代码如下：

      # 计算 softmax
softmax_probs = np.exp(z) / np.sum(np.exp(z), axis=1, keepdims=True)

      • 1
      • 2

    • 计算权重 W 和偏置 b 的梯度。

      要计算Softmax分类的梯度，我们需要求出损失函数对网络输出的偏导数，即 ∂ L ∂ x i \frac{\partial L}{\partial x_i} ∂xi​∂L​。根据链式法则，我们有：
      ∂ L ∂ x i = ∂ L ∂ a i ∂ a i ∂ x i \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial a_i} \frac{\partial a_i}{\partial x_i} ∂xi​∂L​=∂ai​∂L​∂xi​∂ai​​
      其中， ∂ L ∂ a i \frac{\partial L}{\partial a_i} ∂ai​∂L​是损失函数对预测概率的偏导数， ∂ a i ∂ x i \frac{\partial a_i}{\partial x_i} ∂xi​∂ai​​是预测概率对网络输出的偏导数。我们分别求解这两项。

      首先， ∂ L ∂ a i \frac{\partial L}{\partial a_i} ∂ai​∂L​的计算比较简单，根据交叉熵损失函数的定义，我们有：
      ∂ L ∂ a i = − y i a i \frac{\partial L}{\partial a_i} = -\frac{y_i}{a_i} ∂ai​∂L​=−ai​yi​​
      其次， ∂ a i ∂ x i \frac{\partial a_i}{\partial x_i} ∂xi​∂ai​​的计算需要用到Softmax函数的性质，根据Softmax函数的定义，我们有：
      ∂ a i ∂ x i = e x i ∑ k = 1 n e x k − e x i e x i ( ∑ k = 1 n e x k ) 2 = a i − a i 2 = a i ( 1 − a i ) \frac{\partial a_i}{\partial x_i} = \frac{e^{x_i} \sum_{k=1}^n e^{x_k} - e^{x_i} e^{x_i}}{(\sum_{k=1}^n e^{x_k})^2} = a_i - a_i^2 = a_i (1 - a_i) ∂xi​∂ai​​=(∑k=1n​exk​)2exi​∑k=1n​exk​−exi​exi​​=ai​−ai2​=ai​(1−ai​)
      其中，我们用到了分子的求导法则和分母的求导法则，以及指数函数的求导法则。注意，这里的偏导数是对角线元素，即当i=j时的情况。如果 i ≠ j i \neq j i=j，则有：
      ∂ a i ∂ x j = − e x i e x j ( ∑ k = 1 n e x k ) 2 = − a i a j \frac{\partial a_i}{\partial x_j} = \frac{- e^{x_i} e^{x_j}}{(\sum_{k=1}^n e^{x_k})^2} = - a_i a_j ∂xj​∂ai​​=(∑k=1n​exk​)2−exi​exj​​=−ai​aj​
      综上，我们可以得到Softmax分类的梯度的表达式：
      ∂ L ∂ x i = ∂ L ∂ a i ∂ a i ∂ x i = − y i a i a i ( 1 − a i ) = a i − y i \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial a_i} \frac{\partial a_i}{\partial x_i} = -\frac{y_i}{a_i} a_i (1 - a_i) = a_i - y_i ∂xi​∂L​=∂ai​∂L​∂xi​∂ai​​=−ai​yi​​ai​(1−ai​)=ai​−yi​
      这个结果非常简洁，它表示网络输出和真实标签之间的差值。如果我们用向量的形式表示，我们可以写成：
      ∇ x L = a − y \nabla_x L = a - y ∇x​L=a−y
      其中， a a a是预测概率向量， y y y是真实标签向量， ∇ x L \nabla_x L ∇x​L是损失函数对网络输出的梯度向量。这个向量可以用来更新网络的参数，使得损失函数的值降低，预测概率更接近真实标签。

      代码如下：

      # 计算梯度 Δ=a-y(a:预测向量，y：one-hot标签向量)
softmax_grad = softmax_probs.copy()
softmax_grad[np.arange(Input.shape[0]), labels] -= 1
softmax_grad /= Input.shape[0]

# W 和 b 的梯度
self.grad_W = np.dot(Input.T, softmax_grad)
self.grad_b = np.sum(softmax_grad, axis=0, keepdims=True)

      • 1
      • 2
      • 3
      • 4
      • 5
      • 6
      • 7
      • 8

  4. Xavier 权重初始化函数 XavierInit：

    • 使用 Xavier 初始化方法来初始化权重 W 和偏置 b。

​ 这个类的核心是 Softmax 交叉熵损失的计算，以及对应的梯度计算，这在深度学习的训练过程中是非常常见的。

2.3 optimizer.py

这段代码实现了SGD 的类，该类是随机梯度下降（Stochastic Gradient Descent，SGD）优化器的实现。

  1. 初始化函数 __init__：

    • model：待优化的模型对象。
    • learning_rate：学习率，控制权重更新的步长。
    • momentum：动量参数，控制之前梯度的权重。默认为 0.0。

  2. step 方法：

    • 执行一步更新，更新模型的权重。

    • 使用动量的权重更新方法。

    • 对于每个可训练的层，执行以下操作：

      • 如果该层还没有 diff_W 或 diff_b 属性，就将它们初始化为0。

        代码如下：

        if not hasattr(layer, 'diff_W'):
	layer.diff_W = 0.0
if not hasattr(layer, 'diff_b'):
	layer.diff_b = 0.0

        • 1
        • 2
        • 3
        • 4

      • 更新动量 diff_W 和 diff_b。

        带动量的随机梯度下降的参数更新公式如下：
        v t = β v t − 1 − α ∇ J ( θ t ) θ t + 1 = θ t + v t v_t = \beta v_{t-1} -\alpha\nabla J(\theta_t) \\ \theta_{t+1} =\theta_t + v_t vt​=βvt−1​−α∇J(θt​)θt+1​=θt​+vt​
        其中， θ t \theta_t θt​ 是第 t 次迭代的参数， ∇ J ( θ t ) \nabla J(\theta_t) ∇J(θt​) 是第 t 次迭代的梯度， α \alpha α 是学习率， v t v_t vt​ 是第 t t t 次迭代的动量项。

        不带动量的随机梯度下降的参数更新公式如下：
        θ t + 1 = θ t − α ∇ J ( θ t ) \theta_{t+1} = \theta_t - \alpha\nabla J(\theta_t) θt+1​=θt​−α∇J(θt​)
        可以看出，不带动量的随机梯度下降只考虑当前的梯度，而不考虑之前的梯度，因此更新的方向可能会更加随机和不稳定。

        代码如下：

        # 使用动量更新权重 v=av'- ϵΔ(a：动量参数，ϵ：学习率)
layer.diff_W = self.momentum * layer.diff_W - self.learning_rate * layer.grad_W
layer.diff_b = self.momentum * layer.diff_b - self.learning_rate * layer.grad_b

        • 1
        • 2
        • 3

      • 更新权重 W 和偏置 b。

        代码如下：

        # 更新权重 θ=θ+v
layer.W += layer.diff_W
layer.b += layer.diff_b

        • 1
        • 2
        • 3

这个类的主要作用是根据梯度和学习率来更新模型的权重，其中引入了动量来平滑更新过程，提高收敛性。

2.4 dataloader.py

以上代码定义了一个用于处理数据集的类 Dataset，以及用于数据迭代的类 IterationBatchSampler 和 Dataloader。

2.4.1 Dataset 类
  1. 初始化函数 __init__：
    • data_root：数据集根目录。
    • mode：模式，可以是 ‘train’、‘val’ 或 ‘test’。
    • num_classes：类别数量，默认为 10。
  2. __len__ 方法：
    • 返回数据集中样本的数量。
  3. __getitem__ 方法：
    • 根据给定的索引 idx 返回对应的图像和标签。
    • 将图像归一化到 [0, 1] 的范围，并减去均值。
2.4.2 IterationBatchSampler 类
  1. 初始化函数 __init__：
    • dataset：数据集对象。
    • max_epoch：最大的迭代次数。
    • batch_size：每个批次的样本数，默认为 2。
    • shuffle：是否在每个迭代前随机打乱数据。
  2. prepare_epoch_indices 方法：
    • 准备每个迭代的索引。
    • 如果 shuffle 为真，将对索引进行随机打乱。
    • 将索引划分成多个批次，存储在 batch_indices 中。
  3. __iter__ 方法：
    • 返回一个迭代器，用于迭代每个批次的索引。
  4. __len__ 方法：
    • 返回迭代器的长度，即迭代的批次数。
2.4.3 Dataloader 类
  1. 初始化函数 __init__：
    • dataset：数据集对象。
    • sampler：批次采样器对象。
  2. __iter__ 方法：
    • 根据批次索引生成每个批次的图像和标签。
    • 使用 Dataset 中的 __getitem__ 方法获取图像和标签。
  3. __len__ 方法：
    • 返回批次采样器的长度，即迭代的批次数。
2.4.4 build_dataloader 函数
  1. 参数：
    • data_root：数据集根目录。
    • max_epoch：最大的迭代次数。
    • batch_size：每个批次的样本数。
    • shuffle：是否在每个迭代前随机打乱数据，默认为 False。
    • mode：模式，可以是 ‘train’、‘val’ 或 ‘test’。
  2. 返回值：
    • 返回一个 Dataloader 对象，用于加载数据集。

这些类和函数的组合构建了一个数据处理流程，方便在训练和测试过程中加载、迭代和处理数据。

2.5 visualize.py

​ 本代码定义了一个用于可视化损失和准确度曲线的函数 plot_loss_and_acc。

  1. 参数：
    • loss_and_acc_dict：一个字典，包含不同模型或设置下的损失和准确度列表。
  2. 可视化损失曲线：
    • 创建一个新的图形。
    • 初始化 min_loss 和 max_loss 为 100.0 和 0.0。
    • 遍历 loss_and_acc_dict 中的每个键值对，其中键是模型或设置的名称，值是包含损失和准确度列表的元组。
    • 对于每个模型或设置，更新 min_loss 和 max_loss，找到该模型或设置下的最小和最大损失值。
    • 获取当前模型或设置的迭代次数 num_epoch。
    • 使用方块 ('-s') 绘制损失曲线，并以模型或设置的名称作为标签。
    • 设置损失曲线的 x 轴标签为 ‘Epoch’，y 轴标签为 ‘Loss’。
    • 显示图例，设置 x 轴刻度为每两个迭代显示一次，并设置坐标轴范围。
    • 显示损失曲线图。
  3. 可视化准确度曲线：
    • 创建一个新的图形。
    • 初始化 min_acc 和 max_acc 为 1.0 和 0.0。
    • 遍历 loss_and_acc_dict 中的每个键值对，其中键是模型或设置的名称，值是包含损失和准确度列表的元组。
    • 对于每个模型或设置，更新 min_acc 和 max_acc，找到该模型或设置下的最小和最大准确度值。
    • 获取当前模型或设置的迭代次数 num_epoch。
    • 使用方块 ('-s') 绘制准确度曲线，并以模型或设置的名称作为标签。
    • 设置准确度曲线的 x 轴标签为 ‘Epoch’，y 轴标签为 ‘Accuracy’。
    • 显示图例，设置 x 轴刻度为每两个迭代显示一次，并设置坐标轴范围。
    • 显示准确度曲线图。

通过这个函数，可以方便地比较不同模型或设置在训练过程中的损失和准确度趋势，从而更好地了解模型的性能。

3 实验运行

​ 本次试验对比了使用与不使用momentum动量的梯度下降算法，对基于Softmax的手写数字识别的结果。

3.1 无动量的梯度下降

  1. 模型训练

    该代码用给定的配置 cfg 创建一个 Solver 类的实例 runner，并通过 runner.train() 进行模型的训练。

    • 'data_root': 数据集的根目录路径。
    • 'max_epoch': 训练的最大轮次数。
    • 'batch_size': 每个小批次的样本数。
    • 'learning_rate': 学习率，控制权重更新的步长。
    • 'momentum': 动量参数，此处设置为 0，表示不使用动量。
    • 'display_freq': 控制每隔多少个迭代显示一次训练信息。

    代码如下：

    # train without momentum
cfg = {
    'data_root': 'data',
    'max_epoch': 10,
    'batch_size': 100,
    'learning_rate': 0.01,
    'momentum': 0,
    'display_freq': 50,
}

runner = Solver(cfg)
loss1, acc1 = runner.train()

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12

    结果如下：

    Epoch [0][10]	 Batch [0][550]	 Training Loss 2.5201	 Accuracy 0.0800
Epoch [0][10]	 Batch [50][550]	 Training Loss 1.8997	 Accuracy 0.4800
Epoch [0][10]	 Batch [100][550]	 Training Loss 1.6516	 Accuracy 0.5600
Epoch [0][10]	 Batch [150][550]	 Training Loss 1.3129	 Accuracy 0.6800
Epoch [0][10]	 Batch [200][550]	 Training Loss 1.3129	 Accuracy 0.7000
Epoch [0][10]	 Batch [250][550]	 Training Loss 1.1217	 Accuracy 0.7600
Epoch [0][10]	 Batch [300][550]	 Training Loss 0.9862	 Accuracy 0.7600
Epoch [0][10]	 Batch [350][550]	 Training Loss 1.0584	 Accuracy 0.7900
Epoch [0][10]	 Batch [400][550]	 Training Loss 0.8796	 Accuracy 0.8200
Epoch [0][10]	 Batch [450][550]	 Training Loss 0.8113	 Accuracy 0.8500
Epoch [0][10]	 Batch [500][550]	 Training Loss 0.8511	 Accuracy 0.7800

Epoch [0]	 Average training loss 1.2378	 Average training accuracy 0.6812
Epoch [0]	 Average validation loss 0.7118	 Average validation accuracy 0.8656
...
Epoch [9]	 Average training loss 0.4040	 Average training accuracy 0.8901
Epoch [9]	 Average validation loss 0.3151	 Average validation accuracy 0.9200

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17

  2. 性能测试

    该代码用于测试经过训练后的模型在测试集上的性能。

    • 调用 runner.test() 方法，该方法会使用测试集上的样本进行模型的测试，并返回测试损失和测试准确度。
    • 打印输出测试结果。

    代码如下：

    test_loss, test_acc = runner.test()
print('Final test accuracy {:.4f}\n'.format(test_acc))

    • 1
    • 2

    结果如下：

    Final test accuracy 0.9017

    • 1
3.2 带动量的梯度下降

  1. 模型训练

    该代码用给定的配置 cfg 创建一个 Solver 类的实例 runner，并通过 runner.train() 进行模型的训练。

    • 'data_root': 数据集的根目录路径。
    • 'max_epoch': 训练的最大轮次数。
    • 'batch_size': 每个小批次的样本数。
    • 'learning_rate': 学习率，控制权重更新的步长。
    • 'momentum': 动量参数，此处设置为 0.9。
    • 'display_freq': 控制每隔多少个迭代显示一次训练信息。

    代码如下：

    # train with momentum
cfg = {
    'data_root': 'data',
    'max_epoch': 10,
    'batch_size': 100,
    'learning_rate': 0.01,
    'momentum': 0.9,
    'display_freq': 50,
}

runner = Solver(cfg)
loss2, acc2 = runner.train()

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12

    结果如下：

    Epoch [0][10]	 Batch [0][550]	 Training Loss 2.5536	 Accuracy 0.0500
Epoch [0][10]	 Batch [50][550]	 Training Loss 0.8920	 Accuracy 0.7500
Epoch [0][10]	 Batch [100][550]	 Training Loss 0.5691	 Accuracy 0.8700
Epoch [0][10]	 Batch [150][550]	 Training Loss 0.5367	 Accuracy 0.8600
Epoch [0][10]	 Batch [200][550]	 Training Loss 0.5084	 Accuracy 0.8900
Epoch [0][10]	 Batch [250][550]	 Training Loss 0.3843	 Accuracy 0.9000
Epoch [0][10]	 Batch [300][550]	 Training Loss 0.5654	 Accuracy 0.8800
Epoch [0][10]	 Batch [350][550]	 Training Loss 0.3942	 Accuracy 0.9100
Epoch [0][10]	 Batch [400][550]	 Training Loss 0.4692	 Accuracy 0.9100
Epoch [0][10]	 Batch [450][550]	 Training Loss 0.3678	 Accuracy 0.8800
Epoch [0][10]	 Batch [500][550]	 Training Loss 0.3902	 Accuracy 0.9300

Epoch [0]	 Average training loss 0.5806	 Average training accuracy 0.8430
Epoch [0]	 Average validation loss 0.3173	 Average validation accuracy 0.9158
...
Epoch [9]	 Average training loss 0.2929	 Average training accuracy 0.9177
Epoch [9]	 Average validation loss 0.2341	 Average validation accuracy 0.9346

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17

  2. 性能测试

    该代码用于测试经过训练后的模型在测试集上的性能。

    • 调用 runner.test() 方法，该方法会使用测试集上的样本进行模型的测试，并返回测试损失和测试准确度。
    • 打印输出测试结果。

    代码如下：

    test_loss, test_acc = runner.test()
print('Final test accuracy {:.4f}\n'.format(test_acc))

    • 1
    • 2

    结果如下：

    Final test accuracy 0.9220

    • 1

    带动量的梯度下降算法的结果优于不带动量的梯度下降算法。

3.3 可视化图像

该代码使用自定义的 plot_loss_and_acc 函数，将训练过程中的损失和准确度可视化。

代码如下：

plot_loss_and_acc({
    "momentum=0": [loss1, acc1],
    "momentum=0.9": [loss2, acc2]
})

  • 1
  • 2
  • 3
  • 4

  1. 损失曲线
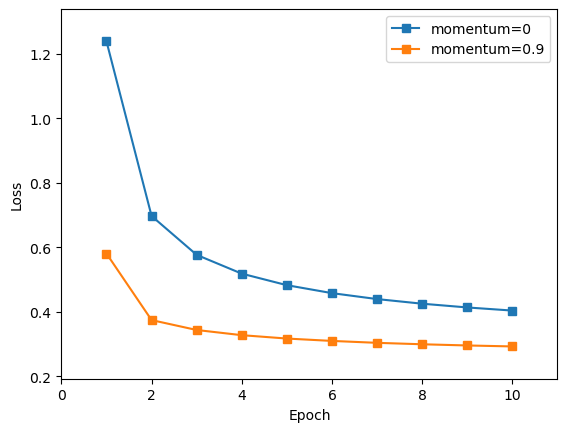
    在这里插入图片描述

  2. 精确度曲线

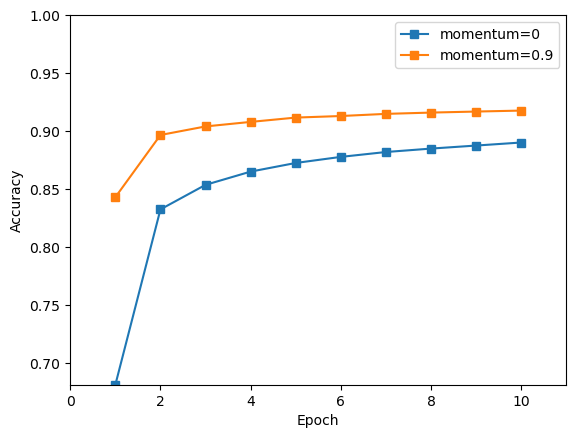
4 总结

​ 通过本次实验设计，更加深入的理解了回归分类算法，包括 softmax 激活函数、交叉熵损失函数、梯度下降算法等。并对深度学习的代码架构有了初步了解，知道了带动量的梯度下降算法的结果，相比于不带动量的梯度下降算法，可以在最初的训练就达到较好的准确率，和较低的loss值，并更快的收敛，收敛的精确度更高，损失也更小。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/67368
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号