知新_RL

这个屌丝很懒，什么也没留下！

热门标签

pytorch基础入门教程_pytorch入门

作者：知新_RL | 2024-06-15 08:39:19

踩

pytorch入门

pytorch基础入门教程

前言

机器学习的门槛并没有想象中那么高，我会陆续把我在学习过程中看过的一些文章和写过的代码以博客的形式分享给大家，和大家一起交流，这个是本系列的第一篇，pytoch入门教程，翻译自pytoch官方文档：Pytorch一小时入门教程。

pytorch是什么

它是一个基于python的科学计算库，致力于为两类用户提供服务：

一些想要找到Numpy搭建神经网络替代品的用户；
寻找一个可提供极强的可拓展性和运行速度的深度学习研究平台；

让我们开始干活吧！

1. 张量的概念和生成

张量和Numpy中ndarrays的概念很相似，有了这个作为基础，张量也可以被运行在GPU上来加速计算，下面介绍如何创建张量。

from __future__ import print_function
import torch
# 这个是用来生成一个为未初始化的5*3的张量，切记不是全零
x = torch.empty(5, 3)
print(x)
"""
tensor([[2.7712e+35, 4.5886e-41, 7.2927e-04],
        [3.0780e-41, 3.8725e+35, 4.5886e-41],
        [4.4446e-17, 4.5886e-41, 3.9665e+35],
        [4.5886e-41, 3.9648e+35, 4.5886e-41],
        [3.8722e+35, 4.5886e-41, 4.4446e-17]])
"""

# 这个是生成一个均匀分布的初始化的，每个元素从0~1的张量，与第一个要区别开，另外，还有其它的随机张量生成函数，如torch.randn()、torch.normal()、torch.linespace()，分别是标准正态分布，离散正态分布，线性间距向量
x = torch.rand(5, 3)
print(x)
"""
tensor([[0.9600, 0.0110, 0.9917],
        [0.9549, 0.1732, 0.7781],
        [0.8098, 0.5300, 0.5747],
        [0.5976, 0.1412, 0.9444],
        [0.6023, 0.7750, 0.5772]])
"""

# 这个是初始化一个全零张量，可以指定每个元素的类型。
x = torch.zeros(5, 3, dtype=torch.long)
print(x)
"""tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])"""

#从已有矩阵转化为张量
x = torch.tensor([5.5, 3])
print(x)
"""
tensor([5.5000, 3.0000])
"""

# 从已有张量中创造一个张量，新的张量将会重用已有张量的属性。如：若不提供新的值，那么每个值的类型将会被重用。
x = x.new_ones(5, 3, dtype=torch.double)      # new_* methods take in sizes
print(x)

x = torch.randn_like(x, dtype=torch.float)    # override dtype!
print(x)                                      # result has the same size
"""
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)
tensor([[ 0.3327, -0.2405, -1.3764],
        [-0.1040, -0.9072,  0.0069],
        [-0.2622,  1.8072,  0.0175],
        [ 0.0572, -0.6766,  1.6201],
        [-0.7197, -1.1166,  1.7308]])
        """

# 最后我们学习如何获取张量的形状，一个小Tip,torch.Size是一个元组，所以支持元组的操作。
print(x.size())
"""torch.Size([5, 3])"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

2. 张量的操作

实际上有很多语法来操作张量，现在我们来看一看加法。

y = torch.rand(5, 3)
# 加法方式1
print(x + y)
"""
tensor([[ 1.2461,  0.6067, -0.9796],
        [ 0.0663, -0.9046,  0.8010],
        [ 0.4199,  1.8893,  0.7887],
        [ 0.6264, -0.2058,  1.8550],
        [ 0.0445, -0.8441,  2.2513]])
"""
# 加法方式2
print(torch.add(x, y))
"""
tensor([[ 1.2461,  0.6067, -0.9796],
        [ 0.0663, -0.9046,  0.8010],
        [ 0.4199,  1.8893,  0.7887],
        [ 0.6264, -0.2058,  1.8550],
        [ 0.0445, -0.8441,  2.2513]])
"""
# 还可以加参数
result = torch.empty(5, 3)
torch.add(x, y, out=result)
print(result)
"""
tensor([[ 1.2461,  0.6067, -0.9796],
        [ 0.0663, -0.9046,  0.8010],
        [ 0.4199,  1.8893,  0.7887],
        [ 0.6264, -0.2058,  1.8550],
        [ 0.0445, -0.8441,  2.2513]])
"""
# 方法二的一种变式，注意有一个‘_’，这个符号在所有替换自身操作符的末尾都有，另外，输出的方式还可以象python一样。
y.add_(x)
print(y)
"""
tensor([[ 1.2461,  0.6067, -0.9796],
        [ 0.0663, -0.9046,  0.8010],
        [ 0.4199,  1.8893,  0.7887],
        [ 0.6264, -0.2058,  1.8550],
        [ 0.0445, -0.8441,  2.2513]])
"""
print(x[:, 1])
"""
tensor([-0.2405, -0.9072,  1.8072, -0.6766, -1.1166])
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

我们现在看一看如何调整张量的形状。

x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1, 8)  # the size -1 is inferred from other dimensions
print(x.size(), y.size(), z.size())
"""
torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8])
"""
1
2
3
4
5
6
7

我们现在看一看如何查看张量的大小。

x = torch.randn(1)
print(x)
print(x.item())
"""
tensor([-1.4743])
-1.4742881059646606
"""
1
2
3
4
5
6
7

到这里，基本的操作知识就已经讲完了，如果了解更详细的部分，请点击这个链接.

3. 张量和Numpy的相互转换

张量和Numpy数组之间的转换十分容易。

Tensor到Nump，在使用Cpu的情况下，张量和array将共享他们的物理位置，改变其中一个的值，另一个也会随之变化。

a = torch.ones(5)
print(a)
"""
tensor([1., 1., 1., 1., 1.])
"""
b = a.numpy()
print(b)
"""
[1. 1. 1. 1. 1.]
"""
a.add_(1)
print(a)
print(b)
"""
tensor([2., 2., 2., 2., 2.])
[2. 2. 2. 2. 2.]
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Numpy到Tensor ，在使用Cpu的情况下，张量和array将共享他们的物理位置，改变其中一个的值，另一个也会随之变化。

import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)
"""
[2. 2. 2. 2. 2.]
tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
"""
1
2
3
4
5
6
7
8
9
10

Gpu下的转换。

# let us run this cell only if CUDA is available
# We will use ``torch.device`` objects to move tensors in and out of GPU
if torch.cuda.is_available():
    device = torch.device("cuda")          # a CUDA device object
    y = torch.ones_like(x, device=device)  # directly create a tensor on GPU
    x = x.to(device)                       # or just use strings ``.to("cuda")``
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))       # ``.to`` can also change dtype together!
"""
tensor([-0.4743], device='cuda:0')
tensor([-0.4743], dtype=torch.float64)
"""
1
2
3
4
5
6
7
8
9
10
11
12
13

自动微分

在pytorch中，神经网络的核心是自动微分，在本节中我们会初探这个部分，也会训练一个小型的神经网络。自动微分包会提供自动微分的操作，它是一个取决于每一轮的运行的库，你的下一次的结果会和你上一轮运行的代码有关，因此，每一轮的结果，有可能都不一样。接下来，让我们来看一些例子。

1. 张量

torch.Tensor是这个包的核心类，如果你设置了它的参数 ‘.requires_grad=true’ 的话，它将会开始去追踪所有的在这个张量上面的运算。当你完成你得计算的时候，你可以调用’backwward()来计算所有的微分。这个向量的梯度将会自动被保存在’grad’这个属性里面。
如果想要阻止张量跟踪历史数据，你可以调用’detach()'来将它从计算历史中分离出来，当然未来所有计算的数据也将不会被保存。或者你可以使用’with torch.no_grad()‘来调用代码块，不光会阻止梯度计算，还会避免使用储存空间，这个在计算模型的时候将会有很大的用处，因为模型梯度计算的这个属性默认是开启的，而我们可能并不需要。
第二个非常重要的类是Function，Tensor和Function,他们两个是相互联系的并且可以搭建一个非循环的运算图。每一个张量都有一个’grad_fn’的属性，它可以调用Function来创建Tensor，当然，如果用户自己创建了Tensor的话，那这个属性自动设置为None。
如果你想要计算引出量的话，你可以调用’.backward()'在Tensor上面，如果Tensor是一个纯数的话，那么你将不必要指明任何参数；如果它不是纯数的话，你需要指明一个和张量形状匹配的梯度的参数。下面来看一些例程。

import torch
x = torch.ones(2, 2, requires_grad=True)
print(x)
"""
tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
"""
y = x + 2
print(y)
"""
tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)
"""
print(y.grad_fn)
"""
<AddBackward0 object at 0x7fc6bd199ac8>
"""
z = y * y * 3
out = z.mean()
print(z, out)
"""
tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)
"""
a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)
"""
False
True
<SumBackward0 object at 0x7fc6bd1b02e8>
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

2. 梯度

现在我们将进行反向梯度传播。因为输出包含一个纯数，那么out.backward()等于out.backward(torch.tensor(1.))；梯度的计算如下（分为数量和向量）

数量的梯度，即各个方向的导数的集合

print(x.grad)
"""
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])
"""
1
2
3
4
5

向量的全微分，即雅可比行列式。
J = ( ∂ y 1 ∂ x 1 ⋯ ∂ y 1 ∂ x n ⋮ ⋱ ⋮ ∂ y m ∂ x 1 ⋯ ∂ y m ∂ x n )

$\begin{aligned} J = (\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \dots & \frac{\partial y_{1}}{\partial x_{n}} \\ ⋮ & ⋱ & ⋮ \\ \frac{\partial y_{m}}{\partial x_{1}} & \dots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}) \end{aligned}$ $\begin{aligned}J=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\end{aligned}$ $J = \frac{\partial y _{1}}{\partial x _{1}} ⋮ \frac{\partial y _{m}}{\partial x _{1}} \dots ⋱ \dots \frac{\partial y _{1}}{\partial x _{n}} ⋮ \frac{\partial y _{m}}{\partial x _{n}}$

J=⎝⎜⎛∂x1∂y1⋮∂x1∂ym⋯⋱⋯∂xn∂y1⋮∂xn∂ym⎠⎟⎞
最后的例子。

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)
"""
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
"""
#停止计算微分
print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
   print((x ** 2).requires_grad)
"""
True
True
False
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

神经网络

神经网络可以用torch.nn构建。现在我们可以来看一看autograd这个部分了，torch.nn依赖于它它来定义模型并做微分，nn.Module包含神经层，forward(input)可以用来返回output.例如，看接下来这个可以给数字图像分层的网络。
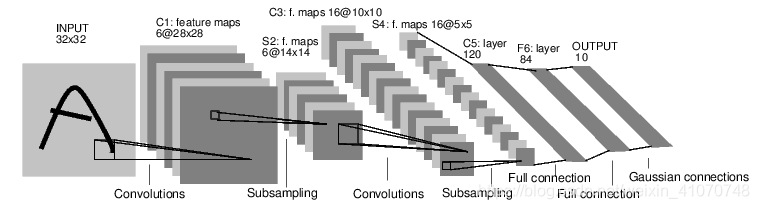
Figure 1.1 convnet

这个是一个简单前馈网络，它将输入经过一层层的传递，最后给出了结果。一个经典的神经网络的学习过程如下所示：

定义神经网络及其参数；
在数据集上多次迭代循环；
通过神经网络处理数据集；
计算损失（输出和正确的结果之间相差的距离）；
用梯度对参数反向影响；
更新神经网络的权重，weight = weight - rate * gradient；

让我们来一步步详解这个过程。

1.定义网络

import torch
import torch.nn as nn
import torch.nn.functional as F


# 汉字均为我个人理解，英文为原文标注。
class Net(nn.Module):

    def __init__(self):
        # 继承原有模型
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        # 定义了两个卷积层
        # 第一层是输入1维的（说明是单通道，灰色的图片）图片，输出6维的的卷积层（说明用到了6个卷积核，而每个卷积核是5*5的）。
        self.conv1 = nn.Conv2d(1, 6, 5)
        # 第一层是输入1维的（说明是单通道，灰色的图片）图片，输出6维的的卷积层（说明用到了6个卷积核，而每个卷积核是5*5的）。
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        # 定义了三个全连接层，即fc1与conv2相连，将16张5*5的卷积网络一维化，并输出120个节点。
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        # 将120个节点转化为84个。
        self.fc2 = nn.Linear(120, 84)
        # 将84个节点输出为10个，即有10个分类结果。
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        # 用relu激活函数作为一个池化层，池化的窗口大小是2*2，这个也与上文的16*5*5的计算结果相符（一开始我没弄懂为什么fc1的输入点数是16*5*5,后来发现，这个例子是建立在lenet5上的）。
        # 这句整体的意思是，先用conv1卷积，然后激活，激活的窗口是2*2。
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        # 作用同上，然后有个需要注意的地方是在窗口是正方形的时候，2的写法等同于（2，2）。
        # 这句整体的意思是，先用conv2卷积，然后激活，激活的窗口是2*2。
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        # 这句整体的意思是，调用下面的定义好的查看特征数量的函数，将我们高维的向量转化为一维。
        x = x.view(-1, self.num_flat_features(x))
        # 用一下全连接层fc1，然后做一个激活。
        x = F.relu(self.fc1(x))
        # 用一下全连接层fc2，然后做一个激活。
        x = F.relu(self.fc2(x))
        # 用一下全连接层fc3。
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        # 承接上文的引用，这里需要注意的是，由于pytorch只接受图片集的输入方式（原文的单词是batch）,所以第一个代表个数的维度被忽略。
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

"""
Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)
"""

# 现在我们已经构建好模型了，但是还没有开始用bp呢，如果你对前面的内容有一些印象的话，你就会想起来不需要我们自己去搭建，我们只需要用某一个属性就可以了，autograd。

# 现在我们需要来看一看我们的模型，下列语句可以帮助你看一下这个模型的一些具体情况。

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

"""
10
torch.Size([6, 1, 5, 5])
"""

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

"""
tensor([[ 0.0114,  0.0476, -0.0647,  0.0381,  0.0088, -0.1024, -0.0354,  0.0220,
         -0.0471,  0.0586]], grad_fn=<AddmmBackward>)
"""

#最后让我们清空缓存，准备下一阶段的任务。
net.zero_grad()
out.backward(torch.randn(1, 10))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

2. 损失函数

先介绍一下损失函数是干什么的：它可以用来度量输出和目标之间的差距，那度量出来有什么意义呢？还记得我们的反向传播吗？他可以将误差作为一个反馈来影响我们之前的参数，更新参数将会在下一节中讲到。当然度量的方法有很多，我们这里选用nn.MSELoss来计算误差，下面接着完善上面的例程。

# 这个框架是来弄明白我们现在做了什么，这个网络张什么样子。
"""
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss
"""
# 到目前为止我们学习了Tensor（张量），autograd.Function（自动微分），Parameter（参数），Module（如何定义，各个层的结构，传播过程）
# 现在我们还要学习损失函数和更新权值。

# 这一部分是来搞定损失函数
output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

# 看一看我们的各个点的结果。
print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

"""
<MseLossBackward object at 0x7efbcad51a58>
<AddmmBackward object at 0x7efbcad51b38>
<AccumulateGrad object at 0x7efbcad51b38>
"""

# 重点来了，反向传播计算梯度。
net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

"""
conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0087, -0.0073,  0.0013,  0.0006, -0.0107, -0.0042])
"""

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

另外官方文档给了一个各个模型和损失函数的地址，有兴趣的可以看一看，或者收藏一下，做个备份。

3. 损失函数

激动人心的时刻终于来了，如何更新权值？如果你对上面我们翻译的文章了解的话，你就知道，我们现在搞定了模型的搭建，也得到了预测值与真实值的差距是多少，在哪里可能造成了这个差距，但是还是短些什么，短什么呢（先自己想一下）？
还剩如何修正这个差距。也就是我们所说的权值更新，我们这个所采用的方法是SGD,学名称为随机梯度下降法 Stochastic Gradient Descent 。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0LsRGcHw-1676447350887)(./5.png)]

# 相应的python代码
learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)
1
2
3
4

如果你想用更多的其它方法的话，你可以查看 t o r c h . o p t i m torch.optim torch.optim。

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update
1
2
3
4
5
6
7
8
9
10
11

至此，我们的基本知识就差不多结束了，接下来我们会动手在CPU和GPU上训练我们的图像分类器。

训练分类器

1. 首先进行数据处理

我们知道，要想有一个好的模型你必须有一些好的数据，并将他们转化为模型可以理解的语言，这个工作非常重要。对于前者我将来会写一个博客介绍我所知道的几种方法，现在我们来看后者。
我们知道，要想有一个好的模型你必须有一些好的数据，并将他们转化为模型可以理解的语言，这个工作非常重要。对于前者我将来会写一个博客介绍我所知道的几种方法，现在我们来看后者如何解决。
众所周知，当我们需要处理图像，文本，音频或者视频数据的时候，你可以使用标准的python库来将这些书v就转化为numpy array，然后你可以其再转化为Tensor。下面列出一些相应的python库：

For images, packages such as Pillow, OpenCV are useful
For audio, packages such as scipy and librosa
For text, either raw Python or Cython based loading, or NLTK and SpaCy are useful

特别是对于视觉领域，我们写了一个叫做torchvision的包，他可以将很多知名数据的数据即涵盖在内。并且，通过torchvision.datasets 和 torch.utils.data.DataLoader 进行数据的转化。在本里中我们将会使用 CIFAR10 数据集，它有以下各类： ‘airplane’, ‘automobile’, ‘bird’, ‘cat’, ‘deer’, ‘dog’, ‘frog’, ‘horse’, ‘ship’, ‘truck’。在这个数据集中的图像尺寸都是3_32_32的。

2. 开始训练模型

先说一下训练步骤.

首先装载数据，并将其统一化；
定义CNN；
定义损失函数；
训练神经网络；
测试网络；

接下来开始干活(cpu版本的)：

import torch
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
                                         shuffle=False, num_workers=2)

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

import matplotlib.pyplot as plt
import numpy as np

# functions to show an image


def imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.show()


# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


net = Net()

for epoch in range(2):  # loop over the dataset multiple times

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs
        inputs, labels = data

        # zero the parameter gradients
        criterion = nn.CrossEntropyLoss()
        optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # print statistics
        running_loss += loss.item()
        if i % 2000 == 1999:    # print every 2000 mini-batches
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

dataiter = iter(testloader)
images, labels = dataiter.next()

# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

outputs = net(images)

_, predicted = torch.max(outputs, 1)

print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
                              for j in range(4)))

correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))

class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs, 1)
        c = (predicted == labels).squeeze()
        for i in range(4):
            label = labels[i]
            class_correct[label] += c[i].item()
            class_total[label] += 1


for i in range(10):
    print('Accuracy of %5s : %2d %%' % (
        classes[i], 100 * class_correct[i] / class_total[i]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141

还没完，还有活干(gpu版本的)：

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Assuming that we are on a CUDA machine, this should print a CUDA device:

print(device)

net.to(device)

inputs, labels = inputs.to(device), labels.to(device)
1
2
3
4
5
6
7
8
9

还没完，还有活干（gpu版本的最终代码成品)：

import torch.optim as optim
import torch
import torchvision
import torchvision.transforms as transforms

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
                                         shuffle=False, num_workers=2)

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

import matplotlib.pyplot as plt
import numpy as np

# functions to show an image


def imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.cpu().numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.show()


# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


net = Net()

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Assuming that we are on a CUDA machine, this should print a CUDA device:

print(device)

net.to(device)



for epoch in range(2):  # loop over the dataset multiple times

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs
        inputs, labels = data
        inputs, labels = inputs.to(device), labels.to(device)
        # zero the parameter gradients
        criterion = nn.CrossEntropyLoss()
        optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # print statistics
        running_loss += loss.item()
        if i % 2000 == 1999:    # print every 2000 mini-batches
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

dataiter = iter(testloader)
images, labels = dataiter.next()
images, labels = inputs.to(device), labels.to(device)

# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

outputs = net(images)

_, predicted = torch.max(outputs, 1)

print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
                              for j in range(4)))

correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        images, labels = inputs.to(device), labels.to(device)
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))

class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
    for data in testloader:
        images, labels = data
        images, labels = inputs.to(device), labels.to(device)
        outputs = net(images)
        _, predicted = torch.max(outputs, 1)
        c = (predicted == labels).squeeze()
        for i in range(4):
            label = labels[i]
            class_correct[label] += c[i].item()
            class_total[label] += 1


for i in range(10):
    print('Accuracy of %5s : %2d %%' % (
        classes[i], 100 * class_correct[i] / class_total[i]))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/721614