知新_RL

这个屌丝很懒，什么也没留下！

热门标签

力扣每日一题刷题总结：链表篇（持续更新）_力扣链表刷题总结

作者：知新_RL | 2024-07-04 00:08:20

踩

力扣链表刷题总结

19. 删除链表的倒数第 N 个结点 Medium 快慢指针、栈 2021/11/19

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。
示例：
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

方法一：最容易想到的，先求链表长，再正序遍历找到要删除结点的前驱结点，然后删除。（这里使用了dummy辅助头结点，可以方便解决只有一个元素的情况）

class Solution {
public:
    int getLength(ListNode* dummy){
        int length = 0;
        while(dummy->next){
            dummy = dummy->next;
            length++; 
        }
        return length;
    }
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(0, head); //辅助头结点，便于删除结点
        ListNode* p = dummy;
        int length = getLength(dummy); //求链表长
        int num = length - n; //指针p需要向右移动的次数
        for(int i = 0; i < num; i++){
            p = p->next;
        }
        p->next = p->next->next;
        return dummy->next;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

方法二：快慢指针思想，先设定快慢指针之间的距离，然后同时向前移动，直到快指针到达链表尾部，此时慢指针指向的即为待删除的结点。

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(0, head); //辅助头结点
        ListNode* fast = dummy; //快指针
        ListNode* slow = dummy; //慢指针
        for(int i = 0; i < n; i++)
        {
            fast = fast->next; //快指针先走几步
        }
        while(fast->next) //快指针和慢指针同时向后移动，直到快指针移动到终点，此时慢指针下一个结点即为要删除的结点
        {
            fast = fast->next;
            slow = slow->next;
        }
        slow->next = slow->next->next; //删除指定结点
        ListNode* newhead = dummy->next; //存储待返回的结点
        delete dummy; //释放辅助头结点
        return newhead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

方法三：利用栈先进后出的性质，依次存储各结点，最后依次弹出，弹第n个后即为要删除的前驱结点

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(0, head);
        stack<ListNode*> s; //使用栈存储各结点指针
        ListNode* p = dummy;
        while(p){
            s.push(p); //各结点入栈
            p = p->next;
        }
        for(int i = 0; i < n; i++){
            s.pop();
        }
        ListNode* p1 = s.top(); //得到待删除结点的前驱结点
        p1->next = p1->next->next;
        ListNode* newhead = dummy->next;
        delete dummy;
        return newhead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

24. 两两交换链表中的节点 Medium 递归 2021/11/19

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。
你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。
示例：
输入：head = [1,2,3,4]
输出：[2,1,4,3]

递归法，非常巧妙，每层将第二个结点的后继连接到第一个结点，第一个结点的后继连接到下一层。

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head || !head->next) return head; //终止条件
        ListNode* one = head;
        ListNode* two = head->next;
        ListNode* three = two->next;
        two->next = one; //将第二个结点的后继连接到第一个结点
        one->next = swapPairs(three); //第一个结点的后继连接到下一层递归
        return two; //每层递归返回第二个节点
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

61. 旋转链表 Medium 链表接环再断裂 2021/11/19

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。
示例：
输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]

方法一：暴力解法，对于每次都调用一次交换的函数

class Solution {
public:
    ListNode* rotateOnce(ListNode* head){
        if(!head || !head->next) return head;
        ListNode *p = head;
        while(p->next->next){
            p = p->next; //找到最后一个结点的前驱节点p
        }
        p->next->next = head; //最后一个结点(p->next)指向第一个结点
        ListNode* newhead = p->next; //保存好最后一个结点，作为第一个结点返回
        p->next = nullptr; //最后一个结点的前驱节点指向空
        return newhead;
    }
    ListNode* rotateRight(ListNode* head, int k) {
        int length = 0; //先求链表长
        ListNode* p = head;
        while(p){
            p = p->next;
            length++;
        }
        if(length == 0) return head; //如果表长为0直接返回
        k = k % length; //由于移动存在周期性，计算实际要移动的次数
        for(int i = 0; i < k; i++){
            head = rotateOnce(head); //重复k次
        }
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

方法二：先把链表接成环，再断裂结点就可达到旋转链表的效果

class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if(!head || !head->next ||k==0) return head;
        int length = 1; //先求链表长，此处从1开始对应while循环中直到p->next为空，为了保留最后一个结点
        ListNode* p = head;
        while(p->next){
            p = p->next;
            length++;
        }
        k = k % length; //由于移动存在周期性，计算实际要移动的次数

        p->next = head; //先将链表接成环形，再断裂
        int num = length - k - 1; //正向遍历次数，归纳总结得出
        ListNode* beforehead = head;
        for(int i = 0; i < num; i++){
            beforehead = beforehead->next; //正向遍历找到要断裂的前驱节点
        }
        ListNode* newhead = beforehead->next; //新头结点
        beforehead->next = nullptr; //要断裂的前驱节点即为尾结点，指向空，即断裂结点
        return newhead; //返回新头结点
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

83. 删除排序链表中的重复元素 Easy 2021/11/20

存在一个按升序排列的链表，给你这个链表的头节点 head ，请你删除所有重复的元素，使每个元素只出现一次。返回同样按升序排列的结果链表。
示例：
输入：head = [1,1,2,3,3]
输出：[1,2,3]

方法一：没有注意到原链表就是升序的，该算法同样适用于不升序的链表，每遇到一个新元素使用set哈希表存储进去，如果碰到的是旧元素则跳过之。

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        ListNode* dummy = new ListNode(0, head); //辅助头结点
        ListNode* p = dummy;
        unordered_set<int> s; //哈希表
        while(p->next){
            if(s.find(p->next->val)==s.end()){ //如果下一结点元素不在set中
                s.insert(p->next->val); //将下一结点元素存入set
                p = p->next; //p后移
            }
            else{ //在set中
                ListNode* del = p->next; 
                p->next = p->next->next; //删除下一结点
                delete del; //释放下一结点空间
            }
        }
        delete dummy; //释放头结点空间
        return head;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

方法二：直接遍历，使用哨兵结点匹配当前结点和下一结点值即可，如果相同则跳过一个结点。

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if(!head || !head->next) return head;
        ListNode* cur = head; //无需哑结点，直接在头结点上操作
        while(cur->next){
            if(cur->val == cur->next->val){ //如果当前结点值等于下一结点值
                ListNode* del = cur->next; 
                cur->next = cur->next->next; //哨兵结点跳过一个结点，指向后一个结点
                delete del;
            }
            else{
                cur = cur->next; //哨兵结点后移
            }
        }
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

82. 删除排序链表中的重复元素 II Medium 迭代、递归 2021/11/20

存在一个按升序排列的链表，给你这个链表的头节点 head ，请你删除链表中所有存在数字重复情况的节点，只保留原始链表中没有重复出现的数字。返回同样按升序排列的结果链表。
示例：
输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

方法一：常规解法：迭代，一次遍历找到后两个val相同的结点，记录该结点值，依次删除所有该值结点并释放。（注意迭代终止条件）

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if(!head || !head->next) return head; //如果链表没有元素或者只有一个元素，直接返回头结点
        ListNode* dummy = new ListNode(0, head); //辅助头结点
        ListNode* cur = dummy; //辅助指针
        while(cur->next && cur->next->next){
            if(cur->next->val != cur->next->next->val){ //如果cur指向的后两个结点值不同
                cur = cur->next; //cur后移
            }
            else{ //如果相同
                int x = cur->next->val; //记录下当前值，删除后面所有为该值的结点
                while(cur->next && cur->next->val == x){ //如果cur后面结点仍为该值且后结点不为空
                    ListNode* del = cur->next;
                    cur->next = cur->next->next; //删除所有为该值的结点
                    delete del;
                }
            }
        }
        ListNode* newhead = dummy->next;
        delete dummy;
        return newhead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

方法二：递归

1.1 递归函数定义
递归最基本的是要明白递归函数的定义！我反复强调过这一点。
递归函数直接使用题目给出的函数 deleteDuplicates(head) ，它的含义是删除以 head 作为开头的有序链表中，值出现重复的节点。

1.2 递归终止条件
终止条件就是能想到的基本的、不用继续递归处理的case。
如果 head 为空，那么肯定没有值出现重复的节点，直接返回 head；
如果 head.next 为空，那么说明链表中只有一个节点，也没有值出现重复的节点，也直接返回 head。

1.3 递归调用
什么时候需要递归呢？我们想一下这两种情况：
如果 head.val != head.next.val ，说明头节点的值不等于下一个节点的值，所以当前的 head 节点必须保留；但是 head.next 节点要不要保留呢？我们还不知道，需要对 head.next 进行递归，即对 head.next 作为头节点的链表，去除值重复的节点。所以 head.next = self.deleteDuplicates(head.next).
如果 head.val == head.next.val ，说明头节点的值等于下一个节点的值，所以当前的 head 节点必须删除，并且 head 之后所有与 head.val 相等的节点也都需要删除；删除到哪个节点为止呢？需要用 move 指针一直向后遍历寻找到与 head.val 不等的节点。此时 move 之前的节点都不保留了，因此返回 deleteDuplicates(move);

1.4 返回结果
题目让我们返回删除了值重复的节点后剩余的链表，结合上面两种递归调用的情况。

如果 head.val != head.next.val ，头结点需要保留，因此返回的是 head；
如果 head.val == head.next.val ，头结点需要删除，需要返回的是deleteDuplicates(move);。

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if(!head || !head->next) return head;
        if(head->val != head->next->val){ //如果首元结点val与下一结点val不相等
            head->next = deleteDuplicates(head->next); //首元节点连接到下一结点的递归
        }
        else{ //如果首结点val与下一结点val相等
            ListNode* move = head->next; //哨兵结点
            while(move && head->val != move->val){ //进行迭代直到为空或与当前首元结点val不相等
                move = move->next; 
            }
            return deleteDuplicates(move); //返回那个结点的递归
        }
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

86. 分隔链表 Medium 队列、头插法创建链表 2021/11/20

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在大于或等于 x 的节点之前。你应当保留两个分区中每个节点的初始相对位置。
示例：
输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

方法一：使用两个队列分别存放小于和大于结点值的结点地址，再组装两个链表，最后将两个链表首尾相接。

class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        queue<ListNode*> less; //利用先进先出规律，使用队列
        queue<ListNode*> more;
        ListNode* cur = head;
        while(cur){ //遍历所有结点
            if(cur->val < x){ //如果结点val值小于x
                less.push(cur); //将其插入less队列
                cur = cur->next;
            }
            else{
                more.push(cur); //如果结点val值大于x
                cur = cur->next; //将其插入more队列
            }
        }
        ListNode* less_list = new ListNode(0, nullptr); //将less队列中的结点组装成链表
        ListNode* cur1 = less_list;
        ListNode* more_list = new ListNode(0, nullptr); //将more队列中的结点组装成链表
        ListNode* cur2 = more_list;
        while(!less.empty()){
            cur1->next = less.front(); //得到less队列首个结点并用cur1指向
            less.pop(); //弹出结点
            cur1 = cur1->next; //cur1指向下个结点
            if(less.empty()){
                cur1->next = nullptr; //如果此时链表为空，尾结点指向空
            }
        }
        while(!more.empty()){ //得到more队列首个结点并用cur2指向
            cur2->next = more.front();
            more.pop(); //弹出结点
            cur2 = cur2->next; //cur2指向下个结点
            if(more.empty()){
                cur2->next = nullptr; //如果此时链表为空，尾结点指向空
            }
        }
        cur1->next = more_list->next; //拼接两个链表，cur1表示less链表尾结点，more_list表示more链表头结点
        ListNode* newlist = less_list->next; //保存头结点以备删除
        delete less_list, more_list;
        return newlist;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

方法二：其实并不需要使用队列，直接遍历原链表，找到符合条件的结点插入到对应的新链表中即可。

class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        ListNode* cur = head;
        //其实并不需要使用队列，直接遍历原链表，找到符合条件的结点插入到对应的新链表中即可
        ListNode* less_list = new ListNode(0, nullptr);
        ListNode* less_cur = less_list;
        ListNode* more_list = new ListNode(0, nullptr);
        ListNode* more_cur = more_list;
        while(cur){
            if(cur->val < x){
                less_cur->next = cur; //如果原链表结点值小于x则插入到less链表中
                less_cur = less_cur->next;
            }
            else{
                more_cur->next = cur; //如果原链表结点值大于x则插入到more链表中
                more_cur = more_cur->next;
            }
            cur = cur->next;
        }
        less_cur->next = nullptr; //将其尾结点都指向空
        more_cur->next = nullptr;
        less_cur->next = more_list->next; //拼接两个链表，cur1表示less链表尾结点，more_list表示more链表头结点
        ListNode* newlist = less_list->next; //保存头结点以备删除
        delete less_list, more_list;
        return newlist;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

141. 环形链表 Easy 快慢指针、散列表 2021/11/22

给你一个链表的头节点 head ，判断链表中是否有环。如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
如果链表中存在环，则返回 true 。否则，返回 false 。输入：
示例：head = [3,2,0,-4] , 有环(3->2->0->-4->2->0…)
输出：true

方法一：使用散列表unordered_set记录链表结点，如果已存在即有环，不存在则加入散列表。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> st; //使用散列表存放结点
        ListNode* cur = head; //辅助指针
        while(cur){ //遍历链表
            if(!st.count(cur)){ //如果没有该结点
                st.insert(cur); //插入该结点
                cur = cur->next;
            }
            else{ //如果已存在该结点
                return true; //有环
            }
        }
        return false; //遍历完没有找到重复结点，无环
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

方法二：快慢指针，利用龟兔赛跑算法原理，快指针每次移动2步，慢指针移动1步，如果快指针在追逐到慢指针之前碰到空，证明无环，如追逐到证明有环。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(!head || !head->next) return false; //如果为空链表或头结点后直接为空，无环
        ListNode* slow = head; //慢指针
        ListNode* fast = head->next; //快指针
        while(slow != fast){
            if(!fast->next || !fast->next->next){ //如果快指针的后两个结点为空
                return false; //必无环
            }
            slow = slow->next; //慢指针向后移动一位
            fast = fast->next->next; //快指针向后移动两位
        }
        return true; //快指针与满指针相遇，有环
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

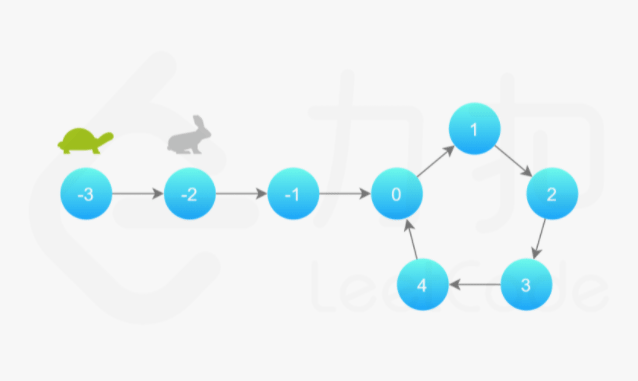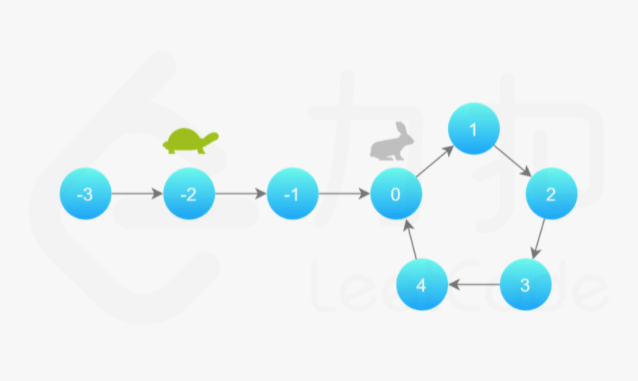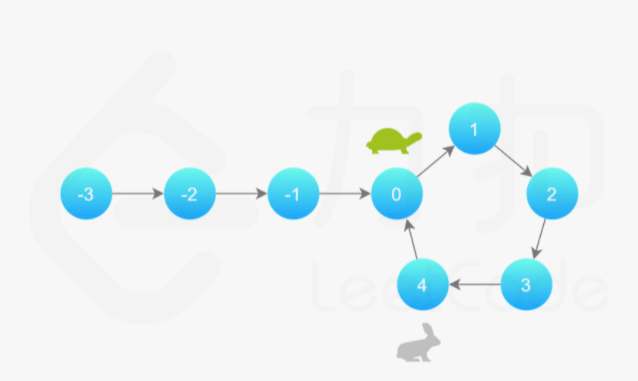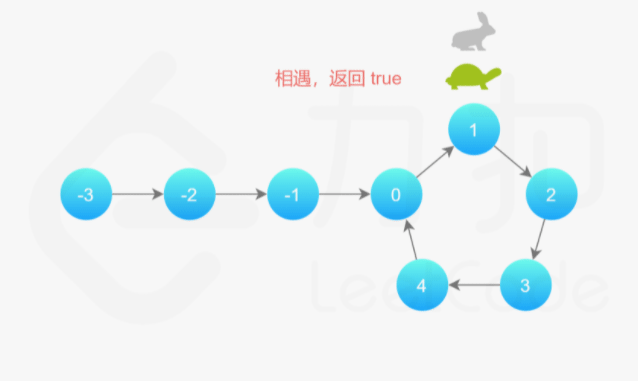
补充：Floyd 判圈算法（又称龟兔赛跑算法）

假想「乌龟」和「兔子」在链表上移动，「兔子」跑得快，「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时，如果该链表中没有环，那么「兔子」将一直处于「乌龟」的前方；如果该链表中有环，那么「兔子」会先于「乌龟」进入环，并且一直在环内移动。等到「乌龟」进入环时，由于「兔子」的速度快，它一定会在某个时刻与乌龟相遇，即套了「乌龟」若干圈。

在这里插入图片描述

142. 环形链表 II Medium 快慢指针、散列表 2021/11/23

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。要求返回环的结点地址。不允许修改链表。
示例：
输入：head = [3,2,0,-4], 有环(3->2->0->-4->2->0…)
输出：返回索引为 1 的链表节点

方法一：使用散列表存放结点指针，同上题方法一。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_set<ListNode*> st; //同上题方法，使用散列表存放结点地址，如果碰到相同的就直接返回
        ListNode* cur = head;
        while(cur){
            if(!st.count(cur)){
                st.insert(cur); //加入散列表
                cur = cur->next; //指向下一结点
            }
            else{
                return cur; //如果碰到相同的就直接返回
            }
        }
        return nullptr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

方法二：快慢指针。当快指针与慢指针相遇后，设辅助指针从头结点出发，和慢指针同时向前走，相遇点即为环点。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head || !head->next) return nullptr;
        ListNode* fast = head->next->next; //快指针先出发两步
        ListNode* slow = head->next; //慢指针只出发一步
        while(fast != slow){
            if(!fast || !fast->next || !fast->next->next){ //如果快指针本身或其后两个为空，则无环
                return nullptr;
            }
            fast = fast->next->next; //快指针走两步
            slow = slow->next; //慢指针走一步
        }
        //跳出while说明此时fast == slow
        ListNode* cur = head; //使用辅助指针cur从head出发
        while(cur != slow){ //在和slow相遇的地方即为环点
            cur = cur->next;
            slow = slow->next;
        }
        return cur;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

理论基础：
根据 2(a+b) = a+(n+1)b+nc，可以推导得 a = c + (n-1)(b+c) 。因此辅助指针从head走到环点的距离恰好等于慢指针从紫色点走到环点的距离（走了c再绕了n-1圈b+c）。

143. 重排链表 Medium 栈、队列、线性表 2021/11/24

给定一个单链表 L 的头节点 head ，单链表 L 表示为：
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为：
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
示例：
输入：head = [1,2,3,4]
输出：[1,4,2,3]

方法一：将链表结点依次放到栈和队列中，依次取出队列的队头元素和栈顶元素并将其组合成新链表。

class Solution {
public:
    void reorderList(ListNode* head) {
        if(!head->next || !head->next->next) return;
        queue<ListNode*> forward; //将各结点放到forward队列中
        stack<ListNode*> reverse; //将各结点放到reverse栈中
        ListNode* cur = head;
        while(cur){
            forward.push(cur);
            reverse.push(cur);
            cur = cur->next;
        }
        ListNode* dummy = new ListNode(0, head);
        cur = dummy;
        //依次取出队列的队头元素和栈顶元素并将其组合成新链表，退出条件是栈顶元素等于队头元素或栈顶元素指向队头元素
        while((reverse.top()->next != forward.front()) && (reverse.top() != forward.front())){
            cur->next = forward.front(); //插入队头
            forward.pop();
            cur = cur->next;
            cur->next = reverse.top(); //插入栈顶
            reverse.pop();
            cur = cur->next;
        }
        //如果因栈顶元素等于队头元素而退出，说明链表元素个数为奇数，需要再插入一下该元素(中间元素)
        if(reverse.top() == forward.front()){
            cur->next = forward.front();
            cur = cur->next;
        }
        cur->next = nullptr; //队尾指向空
        head = dummy->next;
        delete dummy;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

方法二：使用线性表存储各结点，利用线性表随机存取的性质，使用左右指针方便进行重排操作。

class Solution {
public:
    void reorderList(ListNode* head) {
        if(!head || !head->next) return;
        vector<ListNode*> v; //使用线性表存储各结点，因为线性表有随机存取的性质，方便进行操作
        ListNode* cur = head;
        while(cur){
            v.push_back(cur);
            cur = cur->next;
        }
        int i = 0;
        int j = v.size() - 1;
        while(i < j){ //对链表中的元素进行重排，ij为左右指针，直到相遇重排结束
            v[i]->next = v[j];
            i++;
            if(i == j){ //链表元素个数为偶数的情况，直接跳出
                break;
            }
            v[j]->next = v[i];
            j--;
        }
        v[i]->next = nullptr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

方法三：找中间结点（876题）+反转后半段链表（206题）+拼接链表。

class Solution {
public:
    void reorderList(ListNode* head) {
        if(!head->next || !head->next->next) return;
        //第一步：使用快慢指针找到中间结点(如为偶数个结点则找到中间偏前的结点，便于断裂)
        ListNode* slow = head;
        ListNode* fast = head;
        ListNode* before_slow;
        while(fast->next && fast->next->next){
            slow = slow->next;
            fast = fast->next->next;
        }
        ListNode* halfcur = slow->next; //中间结点之后的链表记为halfcur，长度小于等于前半段
        slow->next = nullptr; //将前一段链表断裂
        //第二步：将中间结点(slow)之后的结点(halfcur)链表反转
        ListNode* rev = new ListNode(0, nullptr);
        ListNode* p;
        while(halfcur){
            p = halfcur->next;
            halfcur->next = rev->next;
            rev->next = halfcur;
            halfcur = p;
        }
        ListNode* half = rev->next;
        delete rev;
        //第三步：将两个链表(head, half)拼接起来，这里第一个链表长度必须大于第二个链表长度才能正常拼接
        ListNode* cur1 = head;
        ListNode* cur2 = half;
        ListNode* cur1_temp;
        ListNode* cur2_temp;
        while(cur1 && cur2){
            cur1_temp = cur1->next;
            cur2_temp = cur2->next;
            cur1->next = cur2;
            cur1 = cur1_temp;
            cur2->next = cur1;
            cur2 = cur2_temp;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

206. 反转链表 Easy 迭代、头插法、尾插法、栈 2021/11/24

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。
示例：
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

方法一：迭代法。遍历原链表，建立新链表，对于每个结点进行头插法。这里对新链表使用头结点方便建立链表（其实也可省略但不易于理解）。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(!head || !head->next) return head;
        ListNode* newdummy = new ListNode(0);
        ListNode* p;
        //遍历原链表，建立新链表，对于每个结点进行头插法
        while(head){
            p = head->next; //保存该结点的下一结点
            head->next = newdummy->next; //将结点头插入新链表
            newdummy->next = head; //将结点头插入新链表
            head = p; //结点后移
        }
        ListNode* newhead = newdummy->next;
        delete newdummy;
        return newhead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

不带头结点直接头插（更加简洁）：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* newhead = nullptr; //不带头结点，直接头插
        ListNode* p;
        //遍历原链表，建立新链表，对于每个结点进行头插法
        while(head){
            p = head->next;
            head->next = newhead;
            newhead = head;
            head = p;
        }
        return newhead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

方法二：利用栈，先遍历一遍将各元素压入栈，在使用尾插法建立新链表，容易想到但空间占用较多，时间复杂度为两次遍历。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        stack<ListNode*> stk;
        while(head){
            stk.push(head); //将各结点压入栈
            head = head->next;
        }
        ListNode* newdummy = new ListNode(0, nullptr);
        ListNode* cur = newdummy;
        while(!stk.empty()){
            cur->next = stk.top(); //使用尾插法建立新链表
            stk.pop();
            cur = cur->next;
        }
        cur->next = nullptr;
        ListNode* newhead = newdummy->next;
        delete newdummy;
        return newhead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

92. 反转链表 II Medium 栈、迭代 2021/11/25

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回反转后的链表。
示例：
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

先找到待反转的结点，再使用栈依次将待反转的结点压入栈（这里也可以不用栈使用206题的方法一迭代法反转链表），最后拼接即可。（注意断裂时的链表结点记得保存）。
使用栈的代码：

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        if(!head || !head->next) return head; //如果表长为0或1直接返回
        ListNode* dummy = new ListNode(0, head); //哑结点
        stack<ListNode*> stk; //栈用于存放待反转的结点
        ListNode* cur = dummy; //辅助指针，用于移动到待反转结点的前一个结点
        for(int i = 1; i < left; i++){
            cur = cur->next; //移动left-1次，最后cur停留在待反转结点的前一个结点
        }
        ListNode* p = cur; //辅助指针，用于将各待反转结点压入栈
        for(int j = 0; j <= right - left; j++){
            stk.push(p->next); //将要翻转的结点压入栈，最后p指向待反转结点的最后一个结点
            p = p->next;
        }
        ListNode* latter = p->next; //latter辅助结点指向反转结点后面的结点
        while(!stk.empty()){
            cur->next = stk.top();
            cur = cur->next;
            stk.pop();
        }
        cur->next = latter; //拼接链表
        ListNode* newhead = dummy->next;
        delete dummy;
        return newhead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

876. 链表的中间结点 Easy 快慢指针 2021/11/25

给定一个头结点为 head 的非空单链表，返回链表的中间结点。
如果有两个中间结点，则返回第二个中间结点。
示例：
输入：[1,2,3,4,5]
输出：此列表中的结点 3
输入：[1,2,3,4,5,6]
输出：此列表中的结点 4

快慢指针法可迅速找到中间结点。这里题目要求的是返回后一个中间结点，如要返回前一个将终止条件改为 fast->next && fast->next->next 即可。

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* fast = head; //快指针
        ListNode* slow = head; //慢指针
        while(fast && fast->next){ //跳出条件为fast为空或fast后一结点为空
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow; //返回慢指针
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

234. 回文链表 Easy 数组、快慢指针、反转链表 2021/11/27

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。
示例：
输入：head = [1,2,2,1]
输出：true

方法一：将链表放到数组中，逐个比对对应元素是否相等。

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> v; //都放到数组中
        while(head){
            v.push_back(head->val);
            head = head->next;
        }
        int length = v.size();
        for(int i = 0; i < length / 2; i++){ //比对对应元素是否相等
            if(v[i] != v[length - i - 1]){
                return false;
            }
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

方法二（不推荐）：找中间结点+反转前半链表+逐个比较两个链表val值。此方法相对于方法一空间复杂度低，但极容易出错，需要对偶数和奇数个结点分别进行详细讨论。
此外还可以先记录链表结点数，再使用栈将前半段链表的结点val值存入栈，再依次比较后半段结点val值与栈顶val值，思路较为简单，代码略。

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if(!head || !head->next) return head;
        //第一步：找到中间结点(快慢指针法)
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast && fast->next){
            slow = slow->next; //如有偶数个结点，则指向中间两个的后一个结点
            fast = fast->next->next;
        }
        //第二步：反转前半段链表
        ListNode* newhead = nullptr;
        ListNode* p;
        while(head != slow){
            p = head->next;
            head->next = newhead;
            newhead = head;
            head = p;
        }
        if(fast) slow = slow->next; //如果是因为fast->next为空而跳出的，即链表个数为奇数时，slow后移一位，便于后期比较
        //第三步：逐个比较slow和newhead链表val值
        while(slow){
            if(newhead->val != slow->val){
                return false;
            }
            newhead = newhead->next;
            slow = slow->next;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

剑指 Offer II 028. 展平多级双向链表 Medium 递归栈 2023/2/26

多级双向链表中，除了指向下一个节点和前一个节点指针之外，它还有一个子链表指针，可能指向单独的双向链表。这些子列表也可能会有一个或多个自己的子项，依此类推，生成多级数据结构，如下面的示例所示。
给定位于列表第一级的头节点，请扁平化列表，即将这样的多级双向链表展平成普通的双向链表，使所有结点出现在单级双链表中。
示例：
1—2—3—4—5—6–NULL
|
7—8—9—10–NULL
|
11–12–NULL
变为
1—2—3—7—8—11—12—9—10—4—5—6–NULL

容易想到的是，先递归一遍，找到所有待拼接的首结点，放到栈里，先把所有孩子结点拼完，最后从栈里取结点慢慢拼。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* prev;
    Node* next;
    Node* child;
};
*/

class Solution {
public:
    stack<Node*> s;
    Node* flatten(Node* head) {
        if (!head) return head;
        // 递归一遍，找到所有待拼接的首结点，放到栈里
        dfs(head);
        Node* q = head; 
        while (!s.empty()) {
            while (q->next) q = q->next; // 指针q始终指向最后一个结点
            Node* topNode = s.top();
            s.pop();
            // 做连接
            q->next = topNode;
            topNode->prev = q;
        }
        return head;
    }
    Node* dfs(Node* head) {
        Node* p = head;
        while (p) {
            // 找到有孩子结点的
            if (p->child) {
                if (p->next) s.push(p->next); // 如果其有下一个结点，放到待拼接结点中
                p->child->prev = p;
                p->next = dfs(p->child); // 做连接并向下递归
                p->child = nullptr; // 孩子不要了
            }
            p = p->next;
        } 
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

既然要递归，可以更彻底一点，先递归自己的孩子结点，再递归自己的next结点，全都放在一个vector中，最后一个一个拼接即可。

class Solution {
public:
    vector<Node*> nodes = {};
    Node* flatten(Node* head) {
        dfs(head);
        // 开始拼接
        for (int i = 0; i < (int)nodes.size() - 1; i++) {
            Node* pre = nodes[i];
            Node* cur = nodes[i + 1];
            cur->prev = pre;
            pre->next = cur;
            pre->child = nullptr;
        }
        return head;
    }
    void dfs(Node* head) {
        if (head == nullptr) return;
        nodes.push_back(head);
        // 递归自己的孩子结点和next结点
        dfs(head->child);
        dfs(head->next);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

最优的方法：在递归的同时实现拼接，简洁精炼，需要仔细研读。

class Solution {
public:
    Node* preNode = nullptr; // 前一个节点
    Node* flatten(Node* head) {
        dfs(head);
        return head;  
    }
    void dfs(Node* head)
    {
        if (head == nullptr) return;
        // 拼
        if (preNode != nullptr)
        {
            preNode->next = head;
            head->prev = preNode;
            preNode->child = nullptr;
        }              
        Node* next = head->next; // 提前保存next指针,否则遍历child时候会把上一个节点的next改变 
        preNode = head;  
        dfs(head->child);             
        dfs(next);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

剑指 Offer II 029. 排序的循环链表 Medium 挨着的双指针 2023/2/26

给定循环单调非递减列表中的一个点，写一个函数向这个列表中插入一个新元素 insertVal ，使这个列表仍然是循环升序的。
给定的可以是这个列表中任意一个顶点的指针，并不一定是这个列表中最小元素的指针。
如果有多个满足条件的插入位置，可以选择任意一个位置插入新的值，插入后整个列表仍然保持有序。
如果列表为空（给定的节点是 null），需要创建一个循环有序列表并返回这个节点。否则。请返回原先给定的节点。
示例：
输入：head = [3,4,1], insertVal = 2
输出：[3,4,1,2]

最直接的想法是找到最小值结点和最大值结点，然后去拼，但这样做效率很低，需要遍历两次，且对于 $[1, 1, 3, 3] in ser t Va l = 3$ 这种含有相同最值元素的需要考虑的特别复杂，不推荐。

class Solution {
public:
    Node* insert(Node* head, int insertVal) {
        if (!head) {
            Node* it = new Node(insertVal);
            it->next = it;
            return it;
        }
        Node* p = head;
        Node* minNode = p;
        Node* maxNode = p;
        p = p->next;
        while (p != head) {
            minNode = minNode->val >= p->val ? p : minNode;
            maxNode = maxNode->val <= p->val ? p : maxNode;
            p = p->next;
        }
        // 全是一样的
        if (minNode->val == maxNode->val) {
            maxNode->next = new Node(insertVal, maxNode->next);
            return head;
        }
        while (maxNode->val == maxNode->next->val) maxNode = maxNode->next;
        // 插入值过大或过小，直接在最大结点后面插入
        if (minNode->val >= insertVal || maxNode->val <= insertVal) {
            maxNode->next = new Node(insertVal, maxNode->next);
        }
        else {
            p = minNode;
            while (p->next->val < insertVal) p = p->next;
            p->next = new Node(insertVal, p->next);
        }
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

使用两个挨着的双指针遍历一遍链表，直到找到一个能插入的位置。

class Solution {
public:
    Node* insert(Node* head, int insertVal) {
        Node* node = new Node(insertVal);
        // 空链表
        if (!head) {
            node->next = node;
            return node;
        }
        // 只有一个元素的链表，随便连
        if (!head->next) {
            node->next = head;
            head->next = node;
        }
        Node* pre = head->next;
        Node* cur = head->next->next;
        while (pre != head) {
        	// 可以插入
            if (pre->val <= insertVal && cur->val >= insertVal) break;
            // 元素过大或过小
            if (cur->val < pre->val && (pre->val <= insertVal || cur->val >= insertVal)) break;
            pre = pre->next;
            cur = cur->next;
        }
        pre->next = node;
        node->next = cur;
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/784940