详解基于图卷积的半监督学习_spectral propagation

Kipf和Welling最近发表的一篇论文提出，使用谱传播规则（spectral propagation）快速近似spectral Graph Convolution。

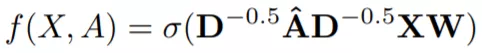
和之前讨论的求和规则和平均规则相比，谱传播规则的不同之处在于聚合函数。它使用提升到负幂的度矩阵D对聚合进行归一化这一点与平均规则类似，但是它的归一化是不对称的。让我们一起来看看。

Aggregation as a weighted sum

我们可以理解，前面提到的聚合函数是加权和，其中每个聚合规则选择不同的权重。在讲解spectral rule之前，先看看平均规则的过程。

The Sum Rule

使用求和规则计算第i个节点的聚合特征，计算过程如下：

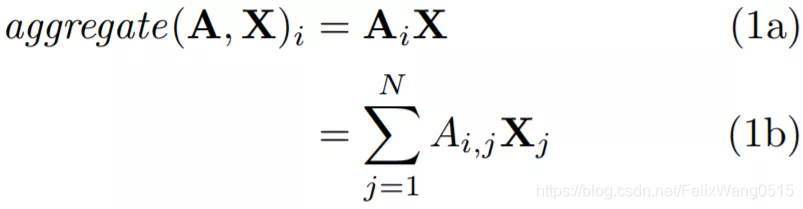
如方程式1a所示，第i个节点的聚合特征表示为向量矩阵乘积，我们可以将这个矩阵乘积表示为一个简单的加权和，如方程1b所示，对X中的每一行求和。

1b中，第j个节点在聚合中的权重由A的第i行、第j列的值确定。由于A是邻接矩阵，当节点j与节点i为邻居时，该值为1，否则为0。因此，1b简化为对第i个节点的邻居节点的特征表示求和。

总的来说，每个邻居的贡献取决于邻接矩阵定义的邻域。

The Mean Rule

要了解平均规则如何聚合节点表示，我们还是看如何计算第i行，现在使用平均规则。为了简单起见，我们只考虑“原始”邻接矩阵上的平均规则，而不考虑A和矩阵I之间的加法，这仅仅对应于向图中添加自循环。

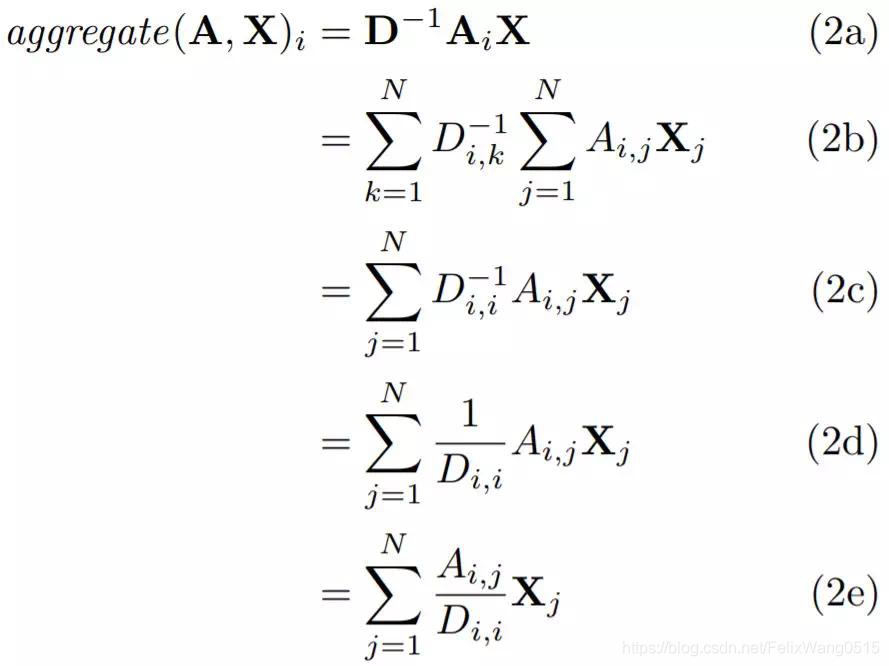
看上面的公式，求导过程明显更长了。在方程2a中，我们首先转换邻接矩阵A，把它乘上D（度矩阵）的逆矩阵。在2b中有更加明确的计算。D-1是一个对角矩阵，沿对角线的值是节点的反度（inverse degree），也就是说位置（i,i）的值是节点i的反度（inverse degree）。因此，我们可以移除其中一个求和符号，得到方程2c。2c可以进一步变形得到2d和2e。

如方程2e所示，我们再次邻接矩阵中的每一行求和。在求和过程中提到的，这相当于对每个节点的邻居求和。不同的是，我们要保证2e中的加权和的权重于第i个节点的度相加等于1。因此，2e对应第i个节点的邻居特征表示的平均值。

The Spectral Rule

那么现在我们来看看Spectral 规则。

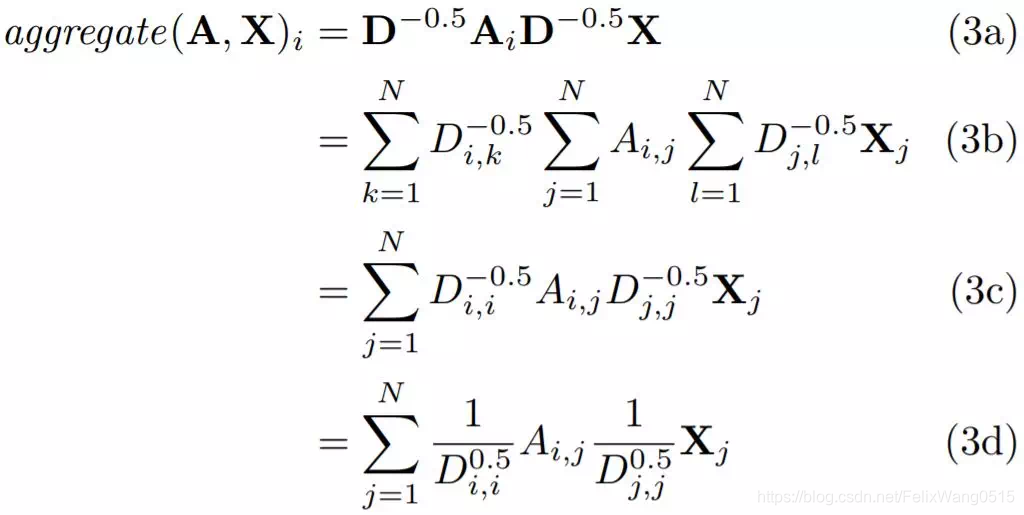
平均规则中，我们使用度矩阵D转换邻接矩阵A。上图中的3a所示，我们将D的幂提高到-0.5，然后乘上矩阵A的每一边。该操作如3b所示，D是对角矩阵，因此我们可以进一步简化方程3b，得到3d。

方程3e很有趣，当我们计算第i个节点的聚合特征表示时，我们不仅要考虑节点i的度，还要考虑节点j的度。

类似平均规则，Spectral 规则对聚合结果进行归一化，使得聚合特征表示与输入特征大致保持相同的比例。不同的是，如果邻居的度低，则加权和中的权重高，如果邻居的度高，则加权和中的权重低。当低度邻居提供比高度邻居更有用的信息时，这种处理便起作用了。

用GCN进行半监督分类

除了Spectral 规则，Kipf和Welling还演示了GCNs用来进行半监督分类。在半监督学习中，我们希望既有标记样本，也有未标记样本。也就是说，我们知道所有的节点，但是不知道所有节点的标签。

在上述的规则中，我们聚合节点邻域，因此共享邻居的节点往往具有相似的特征表示。如果图具有同质性，这属性将很有用，即有连接的节点往往相似（即有相同的标签）。同质性在很多真实的网络中都存在，特别是社交网络。

即使是随机初始化的GCN，仅仅通过使用图结构，也可以很好地分离同质图中节点的特征表示。我们可以在标记节点上训练GCN，通过更新所有节点共享的权重矩阵，有效的将节点标签信息传播给为标记的节点，从而进一步推进上述步骤。具体如下：

1. 通过GCN执行前向传播；
2. 在GCN最后一层逐行应用sigmoid函数；
3. 计算已知节点标签上的交叉熵损失；
4. 反向传播损失并更新每层中的权重矩阵W。

空手道俱乐部的社交网络预测

空手道俱乐部

Zachary空手道俱乐部是一个小型的社交网络，在这里，俱乐部管理员和教练之间会发生冲突。任务是预测，当冲突发生时，俱乐部成员会站在哪一边。俱乐部社交网络图表示如下：

每个节点表示俱乐部的每个成员，成员之间的连接表示他们在俱乐部外进行的交互。管理员用是节点A，教练是节点I。

Spectral Graph Convolutions in MXNet

我使用MXNet实现Spectral 规则，MXNet是一个容易实现的高效的深度学习框架，具体如下：

class SpectralRule(HybridBlock):    
    def __init__(self,                 
                 A, in_units, out_units,                 
                 activation, **kwargs):        
       super().__init__(**kwargs)        
       I = nd.eye(*A.shape)        
       A_hat = A.copy() + I        
       D = nd.sum(A_hat, axis=0)        
       D_inv = D**-0.5        
       D_inv = nd.diag(D_inv)        
       A_hat = D_inv * A_hat * D_inv                
       self.in_units, self.out_units = in_units, out_units                
       with self.name_scope():            
           self.A_hat = self.params.get_constant('A_hat', A_hat)            
           self.W = self.params.get(                
               'W', shape=(self.in_units, self.out_units)            
           )            
           if activation == 'ident':                
               self.activation = lambda X: X            
           else:                
               self.activation = Activation(activation)    
   def hybrid_forward(self, F, X, A_hat, W):        
       aggregate = F.dot(A_hat, X)        
       propagate = self.activation(            
           F.dot(aggregate, W))        
       return propagate
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

建立GCN

根据上面的代码，可以实现Spectral 规则，我们将这些层叠在一起。使用一个两层架构，其中第一个隐藏层有4个单元，第二个隐藏层有两个单元。这种架构可以轻松地显示最终的二维嵌入。有三个值得注意的地方：

1. 我们使用的是Spectral 规则；
2. 激活函数：第一层使用tanh 激活函数，不然的话，死亡神经元的概率很高；第二层使用identity 激活函数，因为最后一层我们要分类节点。

最后，我们在GCN顶部加上逻辑回归层进行节点分类。上述体系结构的python实现如下：

def build_model(A, X):    
    model = HybridSequential()    
    with model.name_scope():        
        features = build_features(A, X)        
        model.add(features)        
        classifier = LogisticRegressor()        
        model.add(classifier)        
        model.initialize(Uniform(1))    
    return model, features
1
2
3
4
5
6
7
8
9

训练GCN

代码如下：

def train(model, features, X, X_train, y_train, epochs):    
    cross_entropy = SigmoidBinaryCrossEntropyLoss(from_sigmoid=True)    
    trainer = Trainer(        
        model.collect_params(), 'sgd',        
        {'learning_rate': 0.001, 'momentum': 1})    
    feature_representations = [features(X).asnumpy()]    
    for e in range(1, epochs + 1):        
        for i, x in enumerate(X_train):            
            y = array(y_train)[i]            
            with autograd.record():                
                pred = model(X)[x] # Get prediction for sample x                
                loss = cross_entropy(pred, y)            
            loss.backward()            
            trainer.step(1)        
       feature_representations.append(features(X).asnumpy())    
    return feature_representations
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

值得注意的是，图中节点只有管理员和教练才打了标签，其余的节点没有。GCN可以找到标记的节点和没有标记的节点表示，并在训练中利用这两种信息来进行半监督学习。具体地，在半监督学习中，GCN通过聚合节点的标签和节点未标记的邻居来产生节点的特征表示。训练过程中，我们反向传播二进制交叉熵损失，以更新所有节点之间的共享权重。而这种损失取决于标记节点的特征表示，而该特征表示又取决于有标签的节点和未标记的节点。

可视化特征 个人觉得此部分讨论讲解较为清楚

正如上面所说，每个时间的特征表示被存储，我们可以看到特征表示在训练期间如何变化。我考虑了两种输入特征表示。

表示一

在第一种表示中，我们简单地使用稀疏34 x 34单位矩阵I，作为特征矩阵X，即one-hot encoding图中的每个节点。这样表示的好处是，可以适用于任何图，但网络中的每个节点都需要输入参数，这需要大量内存和计算能力来训练，并且可能过拟合。幸好空手道俱乐部的网络很小。

通过对网络中的所有节点进行集体分类，我们得到了网络中错误的分布情况，如上所示。这里，黑色表示错误分类。尽管将近一半( 41 % )的节点被错误分类，但与管理员或教练(但不是两者)密切相关的节点倾向于正确分类。

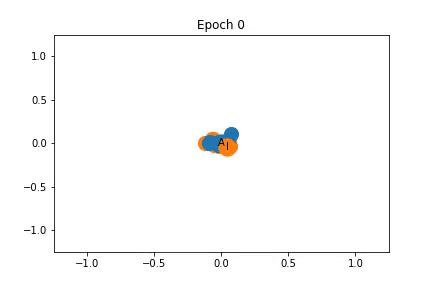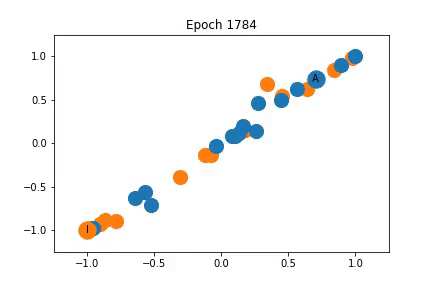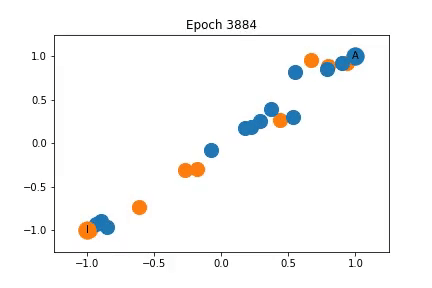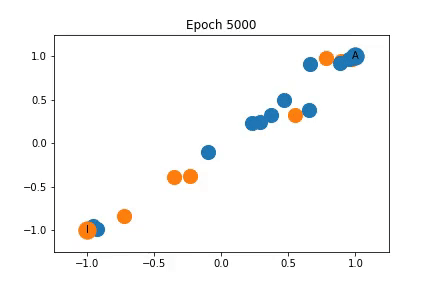
上面我已经说明训练过程中特征表示是如何变化的。最初，节点是密集的聚集在一起，随着训练，教练和管理员被拉开，同时它们拖动一些节点。

虽然教练和管理员的表示不同，但是它们拖动的节点并不一定完全属于它们的社区。

这是因为图卷积嵌入了在特征空间中共享邻居的节点，但是共享邻居的两个节点可能并不等同的连接到管理员和教练。特别是，使用对角矩阵作为特征矩阵导致每个节点高度局部的表示，也就是说在图中相同区域的节点可能紧密嵌入在一起。这使得网络很难以归纳的方式在全局上共享知识。

表示二

我们将改进表示1，改进的方法是增加两个特征，这两个特征不具体到任何一个节点或者网络中的区域，是衡量教练和管理员的连通性。为此，我们计算了网络中每个节点到管理员和教练的最短路径，并将这两个特征连接到前面的表示中。

如前面所述，我们对网络中的所有节点进行了总体分类，并绘制了上图。表示2只有4个节点被错误分类，与表示1相比有了很大的提高。仔细检查特征矩阵后，原因可能是因为这些节点在最短路径上的距离更靠近教练，但它实际上属于管理员社区。

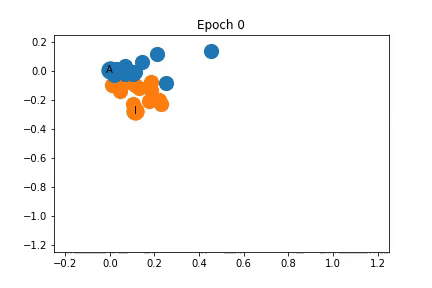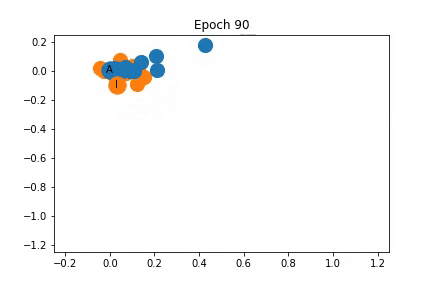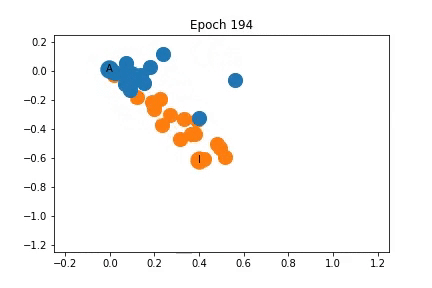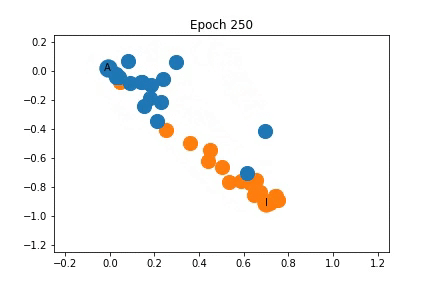
如上所示，节点最初是紧密的聚集在一起，但是在训练开始之前，它在某种程度上已经分成了两个社区，随着训练过程，社区之间的距离增大。

原文链接详解基于图卷积的半监督学习（附代码）