- 1用ChatGPT快速搞定开发、测试、运维实战教程来了,一点代码都不用写!
- 2LeetCode 2208. 将数组和减半的最少操作次数
- 3【Linux】查看已经连接WiFi的密码_system-connections wifi permissions
- 4【Flink状态管理五】Checkpoint的设计与实现_flink的checkpoints的实现方式
- 5ChatTTS 开源文本转语音模型本地部署_chatts 模型下载
- 6【链表OJ 2】反转链表
- 7uniApp map customCallout自定义气泡弹窗_uniapp customcallout
- 8【概率分布】泊松分布(Poisson Distribution)
- 9Unity LuaFramework_unluaframework
- 10保险数字化之路:实现 OMO 一体化的关键步骤
漫步微积分十七——最大最小值问题(续)_用微积分求圆柱体最小表面积
赞
踩
我们用其他的例子继续讨论上一篇文章的基本方法。
例1:圆柱形汤罐头的制造商接了一笔大订单,订单要求罐头的体积为
解:
总的表面积为
我们必须最小化
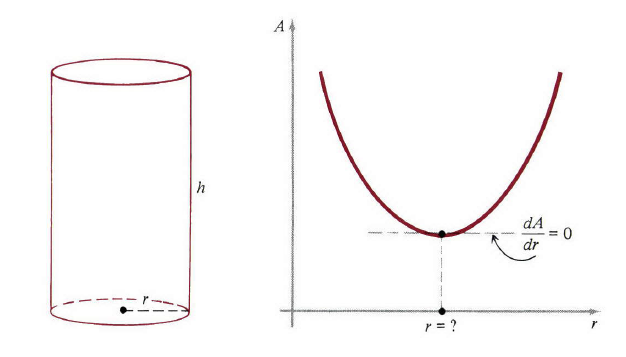
图1
函数图像(图1,右)表明,
如果需要更多参数的解,可以根据等式(4)解出
从中我们可以看到
从降低原材料的角度考虑(最制造商非常重要),这个结果告诉我们圆柱形罐头最好的形状是高等于底的直径。
例2:找出使圆柱体体积最大时的高与直径比。圆柱可以内接于半径为
解:画一个外接球,如图2左,那么我们看到
其中

图2
可视化极端的情况(图2,右),当
求导得
令其等于零得出
最大圆柱的高与直径比为
这个结果利用隐函数求导会效率更高。
根据(5)可得
令上式等于零得到
例3:一束光从点
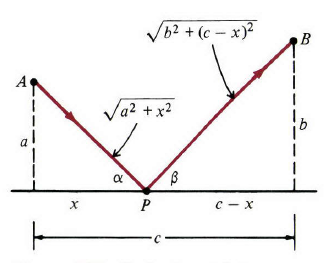
图3
解:将点
求导得
为了最小化
变换一下等式的形式
最后的等式可以轻松的解出
直观上看,很明显,我们可以最小化
(我们跳过了具体计算细节),注意到这个值是正的。
注解1:回顾一下一个锐角
利用此定义,最小化(8)可以重新写为
所以
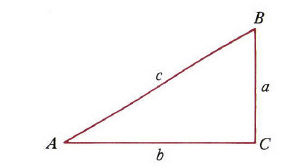
图4}
注解2:例3讨论的反射定律在古希腊时期就存在了。然而,反射光线遵从最短路径这个事实却是很晚之后才被发现,发现者是公元一世纪亚历山大时期的
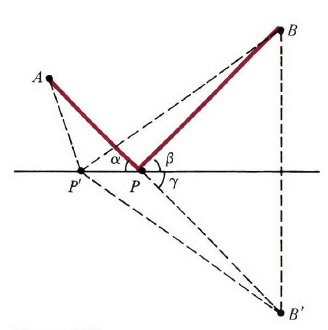
图5
例4:前面讨论的反射光线都是以恒定的速度在单一介质中传播。然而,在不同的介质(水,空气,玻璃)中,光的传播速度不一样。如果光线是从空气进入到水中,如图6,它朝与水面垂直的方向折射(弯曲)。路径
常数与
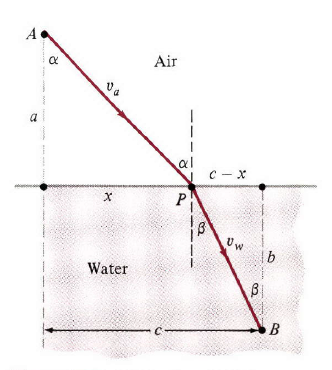
图6
解:如果空气中光的速度为
如果计算这个函数的导数,那么
现在最小化
这是
在例3中,我们可以计算二阶导为正值来证实(11)存在最小值
但是有必要提一下另一种方法。首先观察可得(10)式给出的
注解3:例4的想法是费马在1657年发现的,为此光在光学系统中总是沿最短时间路径传播这个命题叫做费马最短时间原则。(应该注意到,当光在同一均匀介质中传播时,最短路径等价于最短时间)在他之后的两个世纪,费马的想法催生出了许多理论,最大最小原理,欧拉微积分变分法的创立,哈密尔顿的最小行动原则,它是物理学中最统一(
Since the fabric of the world is the most perfect and was established by the wisest Creator,nothing happens in this world in which some reason of maximum or minimum would not come to light.
注解4:
证明它。笛卡尔将他的论点建立在奇特的模型上,根据他的观点,光在高密度的介质中传播速度更快。费马拒绝他的观点(违背常识)。多年来笛卡尔只得被动接受费马的看法但是一直持怀疑态度,直到1657年他证明他的结论是对的,并且伴随着创造出了微积分方法。


